Questo articolo è stato inserito nella sezione d'archivio "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo"

 

L'isola che non c'è, in realtà, c'è ed è legata ad una delle prime curve frattali proposte, ben prima che i frattali fossero introdotti e studiati con grande attenzione. Tutto il quiz è stato "montato" per potere parlare delle sue caratteristiche veramente speciali.

Prima di dare la soluzione al quiz, in forma molto più seria di quanto non sia stato il problema che ho proposto (con un po’ di cattiveria, lo ammetto…), è bene fare una premessa che ci riporta al 1904. Il matematico svedese Helge von Koch pubblica un articolo su una curva che ha ideato (Sur une courbe continue sans tangente, obtenue par une costruction géométrique élémentaire). Una curva fondamentale che anticipa di parecchi anni la nascita dei FRATTALI.

Questa curva ha una estrema importanza “filosofica” e non solo geometrica. Fino a quel momento la geometria descriveva un mondo fantastico, fin dai tempi dei greci e non solo, che raramente riusciva a riprodurre le vere forme della Natura.

Anni più tardi si farà l’esempio della costa della Gran Bretagna, ponendosi la domanda: “Quanto è lunga?”. La risposta imbarazza non poco, dato che si conoscono solo curve che riescono con gran fatica ad approssimare la forma dell’isola. Oltretutto, vi è il problema del livello di precisione che si vuole e qui si apre un vero e proprio collegamento tra infinitamente grande e infinitamente piccolo.

Per una nave di linea si potrebbe dire che la misura è data dal percorso che riesce a mantenere cercando di girare il più possibile vicino alla costa. Per una formica, che può camminare proprio sul bordo della roccia a strapiombo sul mare o lungo il battigia delle spiagge, la lunghezza cambia non poco.

La curva di Koch riesce a quantificare questo tipo di differenza…

Vediamo di costruirla in modo estremamente semplice, come d’altra parte è veramente.

Si prende un segmento qualsiasi, al quale si può dare tranquillamente il valore unitario. Lo si divide in tre parti uguali e su quella centrale si disegna un triangolo equilatero (Fig. 1, in alto)

Si considera solo la linea CONTINUA che contiene i due tratti di segmento lasciati allo stato iniziale e i due lati del triangolo che sporgono verso l’esterno del segmento (Fig. 1, in basso).

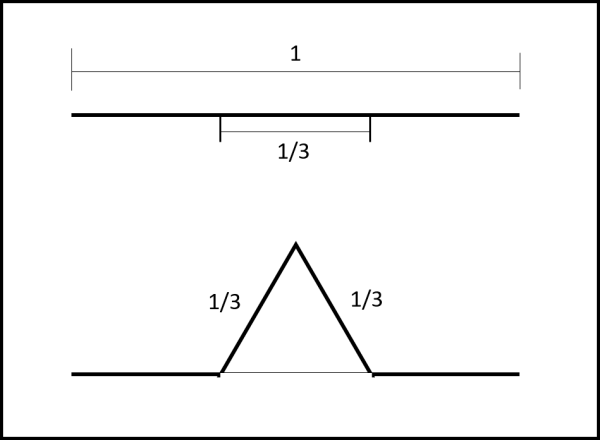
Si nota subito che la lunghezza della nuova curva è uguale ai 4/3 di quella unitaria iniziale.

Su ognuno dei 4 segmenti così ottenuti si ripete il procedimento precedente. Ossia, ogni 1/3 del segmento iniziale viene ad avere 4 segmenti che portano a una lunghezza che è i 4/3 del tratto di segmento (che era 1/3 del segmento originale), Questo procedimento viene fatto per tutti e quattro i lati e si ottengono ora 16 trattini pari a 1/3 del segmento originale uguale a uno.

Si procede con lo stesso meccanismo su tutti i 16 trattini ottenuti nel secondo passaggio… e via dicendo. Quella che si ottiene è la curva di Koch, sicuramente continua, ma non derivabile (Fig. 2)

Non voglio continuare a elencare le sue caratteristiche in questo contesto (questo è il campo di Umberto), ma voglio solo considerare una elaborazione successiva della curva di Koch, che si ottiene partendo da un triangolo equilatero, in modo da ottenere il fiocco di neve di Koch, proprio ciò che ci riconduce alla nostra avventura spaziale.

E’ proprio lui che vogliamo studiare quantitativamente, anche se le sue proprietà differiscono di poco da quelle della curva di partenza. Oltretutto, esso è una curva chiusa e introduce anche il concetto di superficie, che ci porta a un risultato all’apparenza assurdo (che neppure Splashman poteva immaginare).

Il gioco lo conosciamo bene… Per ogni lato del triangolo di partenza eseguiamo quanto fatto per il segmento iniziale della curva di Koch. Non ci vuole molto a capire come si procede e quale fantastico merletto ne viene fuori. Lo possiamo rappresentare nella Fig. 3.

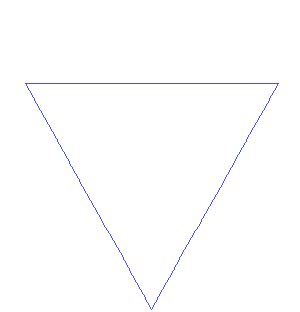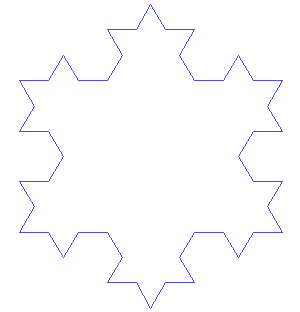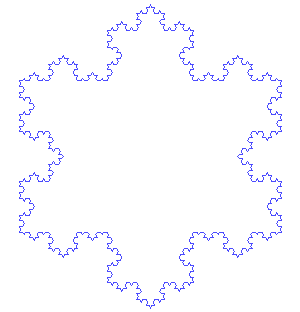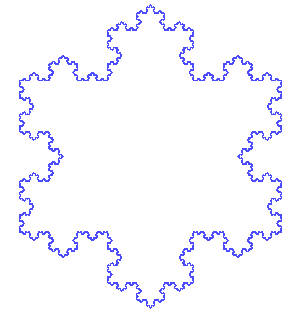
Siamo arrivati a un passo ancora molto piccolo, ma niente ci vieta di continuare anche utilizzando un ... microscopio.

Cominciamo col calcolare l’area del fiocco.

Come si vede dopo il primo passaggio  il triangolino che si aggiunge all’area iniziale, che possiamo nuovamente porre uguale a 1, è uguale a 1/9 dell’area unitaria. Il triangolino del passo dopo continua a essere 1/9 di quello del passo precedente e così via (Fig. 4).

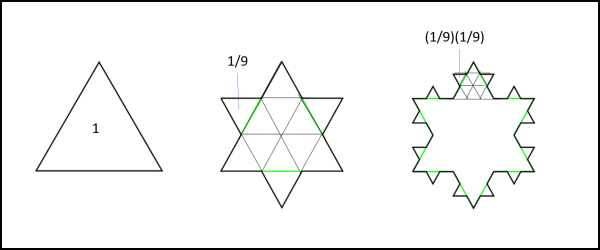
Al primo passo aggiungiamo all’area di partenza tre nuovi triangolini, ossia otteniamo un’area A_TOT pari a

A_TOT = 1 + 3 (1/9)

Nel passo successivo l’area dei nuovi triangolini costruiti su tutti i lati del fiocco di neve (che ancora assomiglia a una stella) è nuovamente pari a 1/9 di quella del triangolino precedente. Quanti nuovi triangolini si sono ottenuti? Presto detto (e contato): 12. Possiamo allora scrivere:

A_TOT = 1 + 3 (1/9) + 12 (1/9) (1/9)

Procedendo nello stesso modo, il passo successivo porta a 48 triangolini (contateli pure) ancora più piccoli, la cui area è sempre 1/9 di quella del triangolino precedente, ossia pari a 1/9 di 1/9 di 1/9 dell’area iniziale.

A_TOT = 1 + 3 (1/9) + 12 (1/9) (1/9) + 48 (1/9) (1/9) (1/9) + …

Non andiamo oltre, ma manipolando un po’ la sommatoria precedente (un bell’esercizio che lascio a voi) si ottiene:

A_TOT = 1 + (1/3)(4/9)⁰ + (1/3)(4/9)¹ + (1/3)(4/9)² + ….

Che possiamo compattare con la sommatoria (con n che va da 0 a infinito)

A_TOT = 1 + (1/3)∑ (4/9)ⁿ

La sommatoria è una serie geometrica la cui ragione r (4/9) è minore di 1. Il che vuol dire che la serie converge e che il suo limite per n che tende a infinito deve essere finito e valere 1/(1- r) (Sulle serie ci torneremo presto, magari affidandoci a Umberto, il grande mago della matematica... per adesso prendete per buono questo risultato),

Nel nostro caso, perciò, il limite per n che tende a infinito di A_TOT, diventa:

A_TOT = 1 +(1/3)(1/(1 - 4/9)) = 1 + (1/3)(1/(5/9)) = 1 + (1/3)(9/5) = 1 + 3/5

A_TOT = 8/5

L’area totale del fiocco di neve diventa poco più grande di due volte quella del triangolo iniziale.

Bene… la nostra ISOLA (ormai avete capito bene come è fatta l’isola che non c’è) ha una superficie decisamente piccola e ben misurabile (anche se non direttamente sul … campo).

Vediamo ora cosa succede al perimetro…

Beh… possiamo decisamente scrivere che esso è dato dal numero dei lati moltiplicato per la lunghezza del lato.

Vediamo prima come varia il numero dei lati…

Al primo passaggio è uguale a 3. Al secondo passaggio deve valere 3∙4 (4 sono i lati appartenenti alle aggiunte fatte per ogni lato originario del triangolo). Al terzo passaggio i lati sono sempre tre volte i lati costruiti su ogni singolo lato originario. Abbiamo, perciò 3∙16 = 3∙4². Successivamente si ottengono 3∙64 = 2∙4³. E via dicendo…

In poche parole matematiche, il termine ennesimo deve essere:

N_n = 3·(4)ⁿ

Calcoliamo adesso il termine ennesimo della lunghezza del singolo lato:

Al primo passaggio è uguale al lato del triangolo originale che poniamo uguale a 1. Poi diventa 1/3 e poi 1/3 di 1/3 e così via. L’ennesimo lato è dato perciò dalla relazione:

L_n = (1/3)ⁿ

Il perimetro P, ennesimo, è quindi uguale a:

P_n = N_n·L_n = 3·(4/3)ⁿ

Il limite per n che tende a infinito è infinito. In poche parole il perimetro dell’isola tende a infinito.

Abbiamo di fronte un’ISOLA davvero fantastica! Essa ha una superficie finita e ben calcolabile, anche per un alieno piccolo piccolo. Tuttavia, essa ha anche un perimetro che tende a infinito.

Ovviamente, il valore infinito si ottiene per una dimensione del lato che tende a zero, ossia per una dimensione di Splashman molto piccola. Ma penso che basti avere le dimensioni di una formica per vederlo nuotare a lungo, molto a lungo… e senza contare il tempo che perde nel dovere sottostare ai continui cambi di direzione causati dai quasi infiniti angoli di 60°.

Non pretendo di entrare nei frattali, di cui questo è solo un antipasto… D’altra parte essi sono un territorio di caccia del nostro Umberto (vedi QUI).

P.S.: GuidoD mi ha fatto presente (forse giustamente) che la definizione periplo perfetto dell'isola non indica esattamente quello che ho cercato di descrivere nel testo romanzato del quiz. In realtà, dovevo parlare di lunghezza perfetta della costa o qualcosa del genere. Ma, forse, avrei dato un aiuto troppo chiaro... Comunque sia, lo scopo finale è stato raggiunto e ci siamo costruiti una figura veramente eccezionale!