Dalla corona circolare a un teorema generale*/****
Un quiz dall'apparenza banale e facilmente risolvibile ha portato a un teorema che nemmeno i greci avevano formulato. Potete fermarvi al livello che volete.
Il quiz introduttivo può essere risolto in vari modi, ma ce n'è uno in particolare che ha avuto applicazioni ben più generali. In questo Circolo sono quasi convinto che qualcuno riuscirà a trovarlo.
Il problema è molto semplice: dati due cerchi concentrici di raggio sconosciuto determinare l'aree della corona circolare definita dai due cerchi conoscendo soltanto la lunghezza di una corda di quello più grande tangente a quello più piccolo.
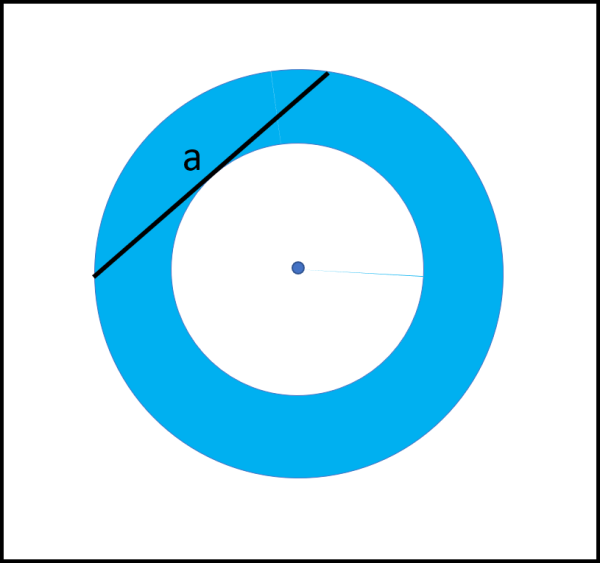
La Figura spiega bene la situazione...
La domanda è la seguente: conoscendo solo a, determinare l'area della corona circolare azzurra.
Mi aspetto tante risposte e, in particolare, quella più difficile ma di grande importanza per molti altri problemi.
P.S.: Il bello, infatti, sarebbe non usare il teorema di Pitagora, ma addirittura ricavarlo...






9 commenti
Provo con la risposta più semplice:
unendo il centro comune delle due circonferenze con il punto medio di a si ottiene il raggio r della circonferenza minore, unendo con uno degli estremi di a si ottiene il raggio R della circonferenza maggiore:
r, R , e a/2 formano un triangolo retto di ipotenusa R e cateti a/2 e r
vale R2- r2 = a2/4
l'area della superfice della corona è
Se do per scontato che la soluzione sia unica, posso considerare anche il caso con il cerchio interno con raggio =0 . Quindi l'area del settore circolare é a^2*pi/4
Caro Fabiopc... che vorrebbe dire r = 0 (un caso particolare del precedente). Manteniamo pure r diverso da zero... ossia il caso più generale.
Fabiopc voleva dire che se l'area è indipendente dai due raggi ma solo dalla corda, allora "qualunque " sia il raggio la formula vale sempre. Prendendo il caso facile r=0, ha risposto al quesito senza usare Pitagora, molto astuto.
dici bene Leandro... e quindi è possibile trovare un metodo che permetta di dire la stessa cosa con R e r qualsiasi, Da qui una nuova dimostrazione del teorema di Pitagora... Mettere r = 0 non basta, ci vuole un passaggio in più...
Una cosa è dire che R = a/2 per r = 0 e un'altra è dire che l'anello equivale sempre a un cerchio di raggio uguale a metà della corda senza usare Pitagora.
Versione corretta (si possono cancellare i miei messaggi precedenti?):
Siano AB la corda nota, r ed R i raggi delle due circonferenze (con R>r), C il centro delle due circonferenze, e T il punto di tangenza della corda AB con la circonferenza più piccola. Inoltre sia α un angolo alla circonferenza che insiste sul minore degli archi AB (quindi 0°<α<90°).
Vogliamo calcolare:
S=π·R²-π·r²=π(R²-r²) (1)
AB=2R·senα (teorema della corda) (2)
La corda AB è tangente alla circonferenza più piccola, quindi il raggio CT è perpendicolare ad AB, ovvero è l'altezza del triangolo ABC.
L'angolo al centro ACB insiste sullo stesso arco dell'angolo alla circonferenza α, quindi ACB=2α.
Il triangolo ABC è isoscele sulla base AB (AC=BC=R), quindi l'altezza CT è anche mediana (da cui AB=2·AT) e bisettrice (da cui ACT=ACB/2=α)
AT=r·tgα (secondo teorema triangoli rettangoli)
AB=2·AT=2r·tgα (3)
Confrontiamo (2) e (3)
2R·senα=2r·tgα
Seconda relazione fondamentale della trigonometria:
R·senα=r·senα/cosα
Semplifichiamo:
R=r/cosα
Ricaviamo cosα:
cosα=r/R (4)
Esprimiamo (2) in funzione di cosα, e utilizziamo (4):
AB=2R·senα=2R·√(1-cos²α)=2R·√[1-(r/R)²]=2R·√[(R²-r²)/R²]=2R·√(R²-r²)/R=2√(R²-r²)
Dividiamo per 2...
√(R²-r²)=AB/2
...ed eleviamo al quadrato:
R²-r²=AB²/4
Sostituiamo il valore di R²-r² nella formula (1):
S=π·AB²/4
Sì, caro Marco... un bel lavoro... Ma io lo vorrei senza trigonometria e MOLTO più semplice (e senza Pitagora).
Sono insaziabile...
Si può usare il primo teorema di Euclide al posto di Pitagora?
unendo il centro comune delle due circonferenze con il punto medio di a si ottiene il raggio r della circonferenza minore, unendo con uno degli estremi di a si ottiene il raggio R della circonferenza maggiore:
r, R , e a/2 formano un triangolo retto di ipotenusa R e cateti a/2 e r (con le rispettive proiezioni sull'ipotenusa)
applicando il primo teorema di Euclide al suddetto triangolo e facendo tutti i calcoli si perviene alla solita relazione cioè R2- r2 = (a/2)2
gira e rigira è sempre Pitagora. No, bisogna pensare "diverso"... Ricorda che il quiz è solo lo spunto per introdurre e analizzare un teorema forse troppo poco conosciuto...
Pensate anche alla talpa terrestre...