Posso dire di essere molto contento, in quanto quello che desideravo si è avverato; lo scopo era trovare una soluzione alternativa ad un problema molto importante  per introdurre la teoria di Ramsey nel piano Euclideo. Ringrazio dunque Vincenzo per essere riuscito in tale intento; il problema non è banale anche se le soluzioni sono semplici. Il quiz lo trovate Qui .

Riporto per prima la soluzione di Vincenzo, così come me l' ha riscritta ( potete trovarne l ' evoluzione nei commenti) e di seguito altre due soluzioni  considerate " ufficiali" .

Soluzione 1:

Il metodo della falsa distanza 

Questo metodo direi che dovrebbe essere considerato più di tipo “astuto” che matematico. Insomma, scegliete voi…

Mi viene fatta la richiesta di dimostrare che data una certa distanza d vi è sempre una coppia di punti dello stesso materiale che distino proprio d.

Inizia la prima parte, quella che chiamerei dello “sprovveduto”. Disegno un triangolo equilatero di lato d e scelgo come vertice un punto d’0ro (O). Se uno qualsiasi degli altri due vertici fosse   d’Oro avrei risolto il problema. Tuttavia, vi sono delle alternative. Ad esempio, almeno uno dei due vertici rimanenti potrebbe essere Argento (A). Rimane un solo vertice, il quale, però, potrebbe essere benissimo diverso da Oro e Argento, ossia essere Bronzo. Il mio triangolo equilatero è sempre costruibile e non ha certo risposto alla richiesta fattami.  Decido, apparentemente, di abbandonare e dire che non sono riuscito nell’impresa…

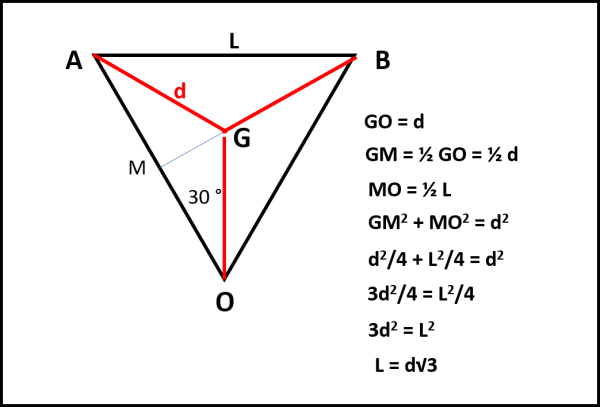
Poi, però, mi blocco e dico: “Aspetta un attimo!”. Il procedimento che ho appena eseguito deve essere sempre applicabile per qualsiasi lato L del triangolo. Perché, allora, non scegliere un lato L tale che sia uguale a d√3? Rifaccio tutto come prima e trovo un triangolo equilatero di lato L che ha i tre vertici di materiale diverso. Beh… cosa avrei risolto? Un bel niente… Ma no, ma no! Qual era la richiesta iniziale? Dimostrare che DEVE esistere sempre una coppia di punti dello stesso materiale che stiano a distanza d. Bene, allora traccio le mediane del triangolo e determino il suo baricentro G. Il baricentro ha però una simpatica caratteristica (ma non solo lui): la sua distanza dai vertici è la stessa ed è proprio uguale a d.

In conclusione, data una qualsiasi distanza d (e quindi anche L), è sempre possibile trovare un punto che sia a quella distanza dai tre vertici che sono, per costruzione, di tre materiali diversi. Ne segue che il baricentro DEVE avere un materiale uguale a uno dei vertici e quindi deve esistere una coppia di materiale uguale la cui distanza reciproca sia proprio d.

Soluzione 2

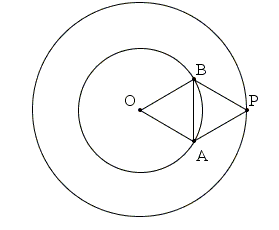
Tracciamo una qualsiasi circonferenza di centro O e raggio    √ 3 d . il punto O sia di argento . Ci sono due possibilità; tutti i punti su quel cerchio sono d'argento o c'è un punto che è bronzo o oro. Nel primo caso, i punti  estremi di qualsiasi corda di lunghezza d saranno dello stesso materiale (argento), risolvendo così il problema ( che tale corda esista è assicurato dal fatto che d è minore del diametro). Altrimenti, mettiamo che ci sia un punto P di bronzo.Troviamo due punti A e B che formano due triangoli equilateri OAB e PAB di lato d . I punti sono le intersezioni dei due cerchi O ( d ) e P ( d ), centrati su O e P ed entrambi con raggio d . Il segmento OP è infatti il diametro ed è il doppio delle due altezze dei due triangoli.

Uno dei punti A e B può essere di argento o di bronzo . Insieme a O o P avremmo una coppia dello stesso materiale. Lo stesso se un punto è di oro e l'altro è argento o bronzo.  Altrimenti, entrambi sono di oro e a distanza d e quindi formano una coppia dello stesso materiale.

Soluzione 3  (dovuta niente meno che a Leo e William Moser, due matematici di un certo rilievo)

Nella figura che ora è conosciuta come Moser Spindle , le distanze AB, AC, AE, AF, BC, BD, EF, FG, DG, EG, CD sono tutte d . Supponiamo che A sia di argento. Se B o C sono dello stesso materiale o uno di questi è di argento, il gioco è fatto. Quindi supponiamo che B sia d'oro e C sia di bronzo. Se D è di bronzo o d'oro, abbiamo finito. Quindi supponiamo che D sia di argento.

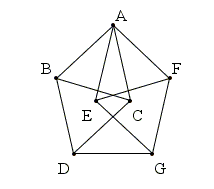
Allo stesso modo, controllando i materiali di E ed F, a meno che non ce ne siano due dello stesso materiale, arriviamo a un G  d'argento, quindi D e G formano una coppia dello stesso materiale.

Ci si pone in modo naturale la seguente domanda:  se ci mettiamo nel piano , qual é il numero minimo di metalli sufficiente per non avere mai due punti dello stesso metallo? Questo sarà l ' obiettivo di un imminente articolo sulle teorie di Ramsey . E la figura di Moser giocherà un ruolo fondamentale nella dimostrazione.

N.B. Questo quiz è la versione "metallica" del più noto problema di colorazione del piano. D'ora in poi useremo anche noi i colori, ma nulla cambia. Una qualsiasi proprietà che distingue in modo univoco i punti del piano andrebbe bene. In realtà la teoria di Ramsey fa parte dell matematica discreta, che si occupa di insiemi o finiti o numerabili. Il problema nel piano Euclideo è una estensione al continuo del problema nel caso discreto.

Fra tutti questi oro argento e ..bronzo non vorrei aver scambiato fra loro qualche metallo. Ho letto e riletto ma prego segnalarmi ogni eventuale refuso. Grazie.