Beh... cari amici, devo dire che il nostro Oreste Pautasso ha cercato veramente di presentarci tutti i 54 metodi di risoluzione della prima parte del QUIZ. Abbiamo dovuto abbatterlo dall'albero su cui si era rifugiato per farlo smettere. Ovviamente, per partito preso e per alto senso democratico, nessuno dei suoi metodi può essere considerato "elegante" come quello che avevo in mente io!

PRIMA PARTE **

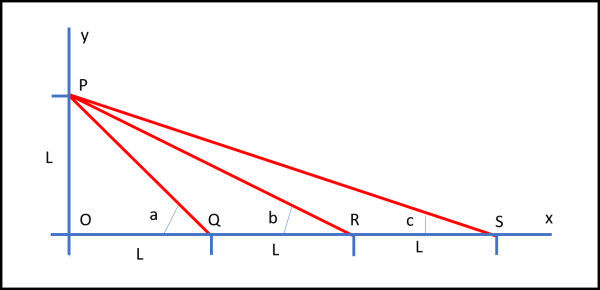
Lo scopo era determinare il valore della somma degli angoli che si ottenevano tracciando rette a partire da uno stesso punto dell'asse y (di ordinata L) fino a punti dell'asse x che crescessero dello stesso valore dell'altezza del punto di origine ( L). Molto meglio richiamarlo con una semplice figura.

Oreste si è scatenato con triangoli simili e rapporti vari. Devo dire con un certo acume, ma -come già detto nei commenti- non è questo il momento giusto per avere RAPPORTI troppo stretti e quindi tutti questi metodi sono stati giustamente vietati dal nostro Governo. E noi ci dobbiamo attenere alle loro lucide argomentazioni, basate su dati di fatto inoppugnabili. Non per niente stiamo studiando alacremente una speciale tuta protettiva che garantisca il "metro di sopravvivenza".

Torniamo a noi e al metodo più ELEGANTE per definizione... (mi sembra di essere il prof. Benigni in Non ci resta che Piangere: "Io, come ho visto quel ragazzino ho subito detto: "Lo boccio!"").

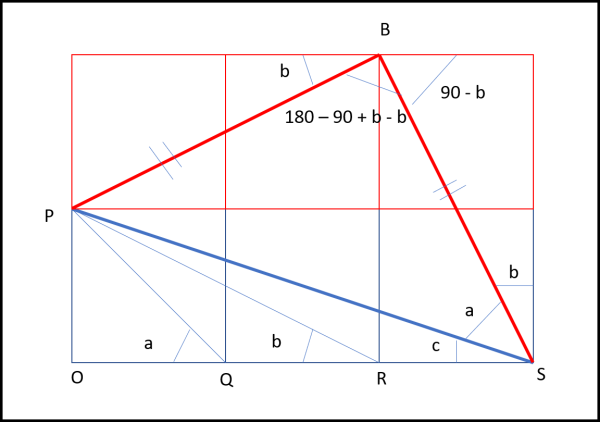
Prendiamo il triangolo POR e riproduciamolo pari pari in SRB. Basta, poi, congiungere P con B. Il triangolo PBS è isoscele per costruzione (PB = PS). L'angolo PBS deve essere di 90°, dato che vale:

180 - 90 + b - b = 90

Ne segue che l'angolo PSB deve essere 45°, ossia uguale ad a. Ne segue che a + b + c = 90°.

Volete mettere che eleganza e senza nessun ... rapporto pericolosissimo!

SECONDA PARTE ****

Sia Arturo che Oreste hanno dato una soluzione che dona il risultato finale corretto. Tuttavia, vorrei presentarvi un metodo molto più rigoroso che ci riporta ancora una volta alla serie armonica  e -soprattutto- a due regole di cui non abbiamo mai parlato.

Richiamiamo, innanzitutto, una certa regola, detta di De l’Hospital, che ci dice che se il limite di un quoziente è del tipo indeterminato 0/0 o ∞/∞ si può  eseguire il limite delle del rapporto delle derivate del numeratore e del denominatore. Se esiste tale  limite, allora esso sarà uguale al limite precedente. Una regola spesso molto utile dato che le funzioni "derivata" sono spesso più semplici della funzione stessa. In termini matematici:

Se

lim _{x→ x0} f(x )/g(x) = 0/0 oppure ∞/∞

ma esiste

lim _{x→ x0}  f’(x)/g’(x) , allora:

lim_{x→ x0} f(x)/g(x) = lim_{x→ x0} f’(x)/g’(x)

Volendo si può ripetere la procedura con le derivate di ordine superiore fino a ottenere un valore non indeterminato (sempre che esista).

La seconda regola da ricordare è quello che viene chiamata Test del Confronto dei Limiti (Limit Comparison Test) e si applica alle serie numeriche.

Essa dice che se abbiamo due serie del tipo ∑a_n e ∑b_n per n che tende a infinito, si può dimostrare che entrambe divergono o convergono se il limite di a_n/b_n, per n che tende a infinito, è maggiore di zero e diverso da infinito. In pratica si applica il Test quando si vuole conoscere la convergenza o la divergenza di una serie. Si calcola, infatti, il limite per n che tende a infinito del rapporto tra il termine della nostra serie e quello di una serie SICURAMENTE convergente o divergente e se il risultato è > 0 e ≠ ∞, anche la nostra serie si comporta come quella già nota.

Andiamo a scrivere la nostra serie relativa alla somma degli angoli… Notiamo immediatamente che per ogni angolo si ha:

L/nL = tan(a)

1/n = tan(a)

In altre parole, l’angolo a qualsiasi vale:

a = atan (1/n)

La nostra somma vale quindi

∑_{n = 1,∞} atan (1/n)

Vogliamo sapere se la nostra serie converge o diverge. Basta confrontarla con un’altra serie che ormai conosciamo molto bene, quella armonica, ossia

∑_{n = 1,∞} (1/n)

Eseguiamo il limite del rapporto dei due membri delle serie e vediamo se il risultato è maggiore di zero e diverso da infinito. Proviamo…

lim_n→∞ atan(1/n)/(1/n)

Purtroppo, sia il numeratore che il denominatore vanno a 0 e siamo di fronte a una forma indeterminata 0/0

Non ci resta che tentare con la regola di De l’Hospital.

Quanto vale la derivata dell’arcotangente? Sappiamo che essa vale:

d/dn(atan(n)) = 1/(1 + n²)

Noi pero abbiamo una funzione di una funzione e dobbiamo ricordarci di effettuare anche la derivata della seconda funzione, ossia:

d/dn(f(g(n)) = f’(g(n))g’(n)

Nel nostro caso f = atan e g = 1/n e quindi:

d/dn(atan(1/n)) = 1/(1 + (1/n)²) d/dn(1/n) = - (1/(1 + (1/n)²)) (1/n²)

Molto più semplice la derivata di 1/n

d/dn(1/n) = - 1/n²

Facendo il rapporto tra la (1) e la (2) si ottiene semplicemente:

1/(1 + (1/n)²)

Passando al limite:

lim_n→∞ 1/(1 + (1/n)²) = 1/1 = 1

Un numero che è maggiore di zero e diverso da infinito. Ne segue che le due serie devono andare di pari passo e, sapendo che quella armonica diverge, deve fare lo stesso anche quella relativa all’arcotangente. In altre parole, la somma degli angoli cresce sempre di più anche se ogni volta si aggiunge un angolo via via più piccolo.

Una volta tanto... ho voluto fare il pignolo!

Il quiz lo trovate QUI