Realtà e rappresentazione : I Modelli matematici *** (Di Maurizio e Umberto)
Questo articolo ha solo tre asterischi, perché il suo scopo primario è di avvicinare il lettore alla comprensione di un semplice modello matematico. Per chi possiede conoscenze approfondite di analisi matematica vengono illustrati i passaggi che giustificano le formule utilizzate.
Introduzione
L’uso di un modello matematico consente di simulare l’andamento nel tempo delle variabili che caratterizzano un sistema ed anche di predire l’effetto della manipolazione di alcune di esse (variabili di controllo) sul comportamento dinamico del sistema. Naturalmente un modello matematico, per essere utilizzabile, deve rispecchiare fedelmente le relazioni causa effetto che si instaurano tra le variabili nel mondo reale, inoltre i valori iniziali di queste variabili devono essere sufficientemente certi. In caso contrario si verificherà una divergenza inevitabile tra la predizione e il comportamento osservabile, Avverrà che alcuni meccanismi “secondari” prenderanno il sopravvento alterando la risposta naturale del sistema.
L’uso di un modello matematico consente di simulare l’andamento nel tempo delle variabili che caratterizzano un sistema ed anche di predire l’effetto della manipolazione di alcune di esse (variabili di controllo) sul comportamento dinamico del sistema. Naturalmente un modello matematico, per essere utilizzabile, deve rispecchiare fedelmente le relazioni causa effetto che si instaurano tra le variabili nel mondo reale, inoltre i valori iniziali di queste variabili devono essere sufficientemente certi. In caso contrario si verificherà una divergenza inevitabile tra la predizione e il comportamento osservabile, Avverrà che alcuni meccanismi “secondari” prenderanno il sopravvento alterando la risposta naturale del sistema.
Ma veniamo ad un esempio ispirato alla vita reale.
La NOVA products, con sede a New York, commercializza prodotti per l’alimentazione e la cura di animali domestici, tipo biscottini, croccantini, spazzole per la toeletta, etc. per cani e gatti. La distribuzione di questi articoli avviene tramite gli stessi clienti, con una modalità di passa-parola. Ai primi clienti è stato proposto di diventare agenti di vendita. Agiranno nei confronti di familiari e amici reclamizzando i prodotti della NOVA e convincendoli ad acquistarli. In più estenderanno anche a loro la possibilità di diventare agenti di vendita e di ottenere ricompense commisurate al volume di affari prodotto. Una specie di catena di Sant’Antonio che si gonfia progressivamente e velocemente, fino a raggiungere un punto in cui la difficoltà di trovare un nuovo adepto diventa predominante. Lo spazio dei potenziali nuovi agenti si è saturato.

Si tratta di un meccanismo simile a quello che si ritrova in natura, nei meccanismi di un contagio. Può anche essere un contagio fecondo ed auspicabile, proprio come quello a cui ci incita dalla nostra Home Page il mitico Albert: “la creatività è contagiosa, trasmettila” oppure un contagio perverso, come la diffusione incontrollabile di fake-news nella rete, futilità o menzogne che rimbalzano in modo caotico da un utente all’altro, al punto che vengono ricevute più volte da uno stesso utente, il tipico video virale.
In epidemiologia, esiste un modello molto semplice per rappresentare questi fenomeni, detto modello SI epidemico, ideale oggetto di studio per il nostro intento didattico.
Il nome SI , in questo modello è la composizione delle iniziali di due parole: S=Suscettibili e I=Infetti
Ma, ispirati dal messaggio di Einstein, che promuove la trasmissione di un valore positivo come la creatività (e la conoscenza), preferiamo associare a queste due iniziali un diverso significato:
Ma, ispirati dal messaggio di Einstein, che promuove la trasmissione di un valore positivo come la creatività (e la conoscenza), preferiamo associare a queste due iniziali un diverso significato:
S= Sprovveduti e I = Istruiti.
S rappresenta il numero di individui Sprovveduti destinati ad essere istruiti (i compratori dei prodotti, alcuni dei quali diventeranno essi stessi istruttori-venditori)
I rappresenta il numero di individui Istruiti sui prodotti. Costoro padroneggiano le tecniche di vendita e trasmetteranno il loro sapere trasformando gli Sprovveduti in Istruiti.
S rappresenta il numero di individui Sprovveduti destinati ad essere istruiti (i compratori dei prodotti, alcuni dei quali diventeranno essi stessi istruttori-venditori)
I rappresenta il numero di individui Istruiti sui prodotti. Costoro padroneggiano le tecniche di vendita e trasmetteranno il loro sapere trasformando gli Sprovveduti in Istruiti.
Indichiamo infine con N il numero totale di persone che costituiscono la popolazione, sarà quindi N=S+I
Immaginiamo che nel periodo di tempo in cui si svolge tutta la vicenda, non nascano figli (Sprovveduti) nella popolazione degli Sprovveduti né figli (Istruiti) nella popolazione degli Istruiti, e supponiamo anche che nessuno degli individui presenti scompaia dalla scena. La stabilità di queste popolazioni ci consente, a tutto diritto, di utilizzare questo semplice modello SI.
Immaginiamo che nel periodo di tempo in cui si svolge tutta la vicenda, non nascano figli (Sprovveduti) nella popolazione degli Sprovveduti né figli (Istruiti) nella popolazione degli Istruiti, e supponiamo anche che nessuno degli individui presenti scompaia dalla scena. La stabilità di queste popolazioni ci consente, a tutto diritto, di utilizzare questo semplice modello SI.
Sappiamo anche che in realtà il risultato di un processo educativo non è sempre permanente. Avete presente il cosiddetto “analfabetismo di ritorno”? Si tratta di quel disgraziato fenomeno che in Italia si verifica nel 30% della popolazione, per cui le conoscenze acquisite (come capacità di lettura, scrittura, comprensione, calcolo) vengono perse per mancanza di esercizio di quanto imparato. http://www.askanews.it/cultura/2019/01/22/il-30-degli-italiani-%c3%a8-analfabeta-di-ritorno-dati-fondazione-feltrinelli-top10_20190122_171323/
Nel caso volessimo tener conto di questa cancellazione della memoria, dovremmo gestire una fluttuazione tra la popolazione S e la popolazione I; insomma, alcuni Istruiti (temporanei) tornerebbero ad essere Sprovveduti e il modello si complicherebbe, avrebbe una dinamica SIS (da Sprovveduto a Istruito e di nuovo da Istruito a Sprovveduto) un tragitto doloroso che mi ricorda un famoso e meraviglioso racconto di Daniel Keys, intitolato “Fiori per Algernoon” la cui trama è descritta a questo link. https://it.wikipedia.org/wiki/Fiori_per_Algernon
Non è però questo il caso che desideriamo trattare nel presente articolo, in cui ci atteniamo esclusivamente allo schema, più semplice, del modello SI.
L'incidenza standard
La probabilità di passare dal gruppo S al gruppo I è legata al numero di incontri che avvengono tra il singolo Istruito ed i componenti della comunità degli Sprovveduti.
Il manuale della NOVA contiene vari consigli per trasmettere efficacemente la conoscenza agli Sprovveduti
La probabilità di passare dal gruppo S al gruppo I è legata al numero di incontri che avvengono tra il singolo Istruito ed i componenti della comunità degli Sprovveduti.
Il manuale della NOVA contiene vari consigli per trasmettere efficacemente la conoscenza agli Sprovveduti
Eccone alcuni …
Parti da te stesso, scegli i prodotti che vuoi usare tu per primo!
Preparati alle novità con tutti gli strumenti a disposizione (NOVA per Te, sito NOVA.it, My Nova Store, My Nova App e catalogo Flash)
Coinvolgi il Cliente: porta con te il Catalogo e cerca sempre nuovi contatti
Proponi l’attività a tutte le persone che incontri e parla di Nova ad almeno 10 persone al giorno
Parti da te stesso, scegli i prodotti che vuoi usare tu per primo!
Preparati alle novità con tutti gli strumenti a disposizione (NOVA per Te, sito NOVA.it, My Nova Store, My Nova App e catalogo Flash)
Coinvolgi il Cliente: porta con te il Catalogo e cerca sempre nuovi contatti
Proponi l’attività a tutte le persone che incontri e parla di Nova ad almeno 10 persone al giorno
Studiando la situazione in una certa zona geografica dove la Nova Products si è insediata da tempo, dopo varie considerazioni (di tipo anche sperimentale, ovvero statistiche), si è arrivati a definire una relazione tra i valori di S, I e N, che è una relazione indispensabile per esprimere le nostre future equazioni, ed è di questo tipo:
1)
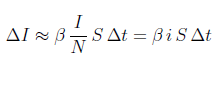
(ove si pone i/N=I).
dove in simbolo 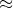 indica che l'identità tra i due termini vale solo nel senso della legge dei grandi numeri.
indica che l'identità tra i due termini vale solo nel senso della legge dei grandi numeri.
Il coefficiente può essere interpretato come il numero medio di contatti a persona , per unità di tempo, attraverso i quali avviene la trasmissione della conoscenza e la conseguente trasformazione di Sprovveduti in Istruiti (ricordiamo che noi siamo interessati all'evolversi del processo di istruzione nel tempo, quindi anche S e I saranno funzioni del tempo S(t),I(t)).
(d'ora in poi useremo un linguaggio consistente in termini di analisi matematica; tuttavia non possiamo studiare un processo di tale tipo in altro modo)
Bene, per poter impostare una equazione che ci darà poi l'andamento delle funzioni che ci interessano, dobbiamo mettere la 1) in forma differenziale, passando al limite per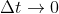 , dividendo prima per
, dividendo prima per 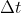 . Nel caso di popolazione costante (N=N0) N non dipende dal tempo, quindi otteniamo
. Nel caso di popolazione costante (N=N0) N non dipende dal tempo, quindi otteniamo
2)
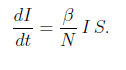
Poniamo poi s=S/N, i=I/N
Notiamo anche che con queste notazioni, s+i=1 (S/N+I/N=(S+I)/N=N/N=1)
e inoltre la 2) diventa:
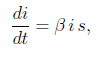
.
quindi possiamo impostare due equazioni differenziali:
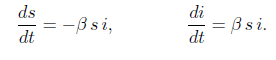
come notato prima
Utilizzando questa relazione è possibile scrivere un'equazione scalare per la singola quantità s (o per i)
infatti =\beta&space;s&space;(s-1))
ponendo
l'equazione diventa:
infatti :
la sostituzione con 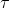 è un trucco per risolvere l'equazione differenziale
è un trucco per risolvere l'equazione differenziale )) . Se adesso invertiamo il denominatore della "frazione"
. Se adesso invertiamo il denominatore della "frazione" 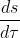 otteniamo:
otteniamo: }) ;
; }ds) =
=ds)
il metodo che stiamo usando è noto come separazione di variabili . Perchè si chiama così? Perchè s compare sia a destra che a sinistra dell'equazione differenziale, ma noi dobbiamo separarle mettendo le variabili a destra e sinistra singolarmente, per poterle integrare. Chi non conosce tale metodo di integrazione può passare direttamente al punto 3)).
In definitiva:
possiamo integrare entrambi i membri di questa equazione (ricordo che entrambi dipendono dal tempo t),
cioè trovare le due primitive:
Troviamo per prima cosa le due primitive:
una chiaramente è 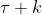 , l'altra è :
, l'altra è :
Dove abbiamo usato il fatto che la derivata di =\frac{1}{x}) e che la differenza dei logaritmi equivale al logaritmo del rapporto.
e che la differenza dei logaritmi equivale al logaritmo del rapporto.
Visto che k,k1 sono delle costanti possiamo inglobarle in una unica costante C, ottenendo:
Intervengono poi i valori iniziali del problema (detto anche problema di Cauchy ); ( s(0) il numero degli Sprovveduti all'istante t= 0, e i(0)=, il numero di Istruiti al tempo 0, naturalmente in percentuale rispetto ad N).
elevando desso e hai due esponenti sopra otteniamo:
da cui, saltando qualche conto algebrico:
ma essendo i+s=1, 1-s=i sempre, risulta:
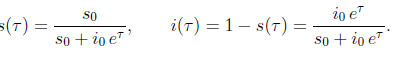
Tornando al numeri assoluti, cioè moltiplicando per N, e sostituendo a 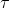 il suo valore, ossia
il suo valore, ossia 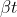 , otteniamo le nostre due funzioni del tempo:
, otteniamo le nostre due funzioni del tempo:
3)
Funzioni che esprimono l'evolversi nel tempo dei soggetti Sprovveduti e di quelli Istruiti, partendo dai valori iniziali So e Io all'istante 0.
(notare che S(t)--->0, I(t)--->N per t tendente a infinito, ossia asintoticamente)
(notare che S(t)--->0, I(t)--->N per t tendente a infinito, ossia asintoticamente)
La cosa che interessa di più è la curva cosiddetta epidemica, cioè la curva che associa al tempo t, il tasso di crescita della trasformazione degli Sprovveduti in Istruiti:
Essa si ottiene derivando la funzione I(t). rispetto al tempo (cosa che lasciamo ai più volenterosi)
Ma in quale istante si raggiungerà la massima conversione degli Sprovveduti in Istruiti ?
Studiando la funzione (cercasi volenteroso), si ottiene che essa presenta un massimo, il cosiddetto valore di picco, per il valore di tempo:
nel qual caso si ha:
Guarda un po’ che strano... quando la metà della popolazione è stata trasformata da uno stato all’altro, proprio
in questo preciso momento, inizia una sistemica difficoltà nel riuscire trasformare in Istruiti i restanti Sprovveduti.
La nutrita schiera dei venditori di biscottini fatica a trovare nuovi adepti per farne altrettanti venditori dei rinomati prodotti della NOVA Products, sede a New York e filiali in tutto il pianeta.
in questo preciso momento, inizia una sistemica difficoltà nel riuscire trasformare in Istruiti i restanti Sprovveduti.
La nutrita schiera dei venditori di biscottini fatica a trovare nuovi adepti per farne altrettanti venditori dei rinomati prodotti della NOVA Products, sede a New York e filiali in tutto il pianeta.






6 commenti
bel lavoro amici!!!
Possiamo ipotizzare di sostituire istruiti e sprovveduti con massa di elio e massa di idrogeno in una stella ? Penso che le equazioni si complichino un po', però il concetto rimane valido: quando tutto l'idrogeno si sarà fuso rimarrà solo elio e la stella uscirà dalla sequenza principale. Ovviamene la sella non è un sistema isolato e una parte dell'energia si diperderà nello spazio. Però possiamo misurare la posizione del nostro sole in questa equazione?
Beh... non funziona proprio così. In una stella non c'è bisogno che tutto l'idrogeno venga fuso, ma solo il nucleo centrale che raggiunge una certa temperatura. A quel punto uscirà dalla sequenza e inizierà a bruciare uno strato di idrogeno dopo essersi contratta, E poi, finalmente, riuscirà a bruciare l'elio, ecc., ecc. Esistono già i modelli e sono piuttosto diversi da questo...
Grazie
Grazie , Enzo.
Da lontani ricordi di chimica mi verrebbe da fare una analogia con la legge dell'equilibrio mobile di Le Chatellier, per la quale una variazione di concentrazione dei reagenti provoca una reazione nel sistema, che tende a controbilanciare la variazione. Insomma, un sistema in equilibrio cerca di opporsi come può alla perturbazione e ristabilire una nuova condizione di equilibrio.
Non escludo che l'analogia sia solo apparente.
In qualche modo, come per il clima terrestre (in piccolo e alla lontana), c'è una specie di feedback. Gli effetti cambiano le cause stesse che li hanno procurati. Inoltre, i parametri in gioco sono molteplici, come l'aumento del volume dovuto al riscaldamento degli strati superficiali, contrapposto alla concentrazione del nucleo. Insomma, le stelle sanno come trovare l'equilibrio finché riescono... e non ci sono mai state stelle in preda a mancanza di idrogeno e l'ossigeno sanno anche crearselo da sole, nel caso ...