La frase del titolo è stata detta da un genio della matematica come Paul Herdos (1913-1996) e se lo ha detto lui c'è da crederci...

Vogliamo trattare un problema apparentemente semplice, ma la cui soluzione è ancora ben lontana dall'essere avvicinata anche attraverso i supercomputer. In poche parole non sappiamo ancora se una certa congettura è vera o falsa e, in ogni caso, non se ne capisce l'essenza stessa.

Stiamo parlando della congettura di Collatz, enunciata nel 1937 da Lothar Collatz (1910-1990) e poi riproposta da svariati matematici. Essa rappresenta, forse, la congettura più semplice da comprendere, ma più difficile da dimostrare...

Consideriamo un numero n intero positivo qualsiasi di partenza diverso da uno e si agisca come segue:

Se n è pari si divida per due

N = n/2

Se n è dispari si moltiplichi per tre e si aggiunga uno

N = 3n + 1

A ogni nuovo numero così ottenuto si applichi di nuovo lo stesso processo.

Bene, qualsiasi sia il numero di partenza la serie di numeri trovati finisce con il numero 1.

Proviamo?

n = 5

N1 = 3 · 5 + 1 = 15 + 1 = 16

N2 = 16/2 = 8

N3 = 8/2 = 4

N4 =4/2 = 2

N5 = 2/2 = 1

Dopo di che l'algoritmo termina.

Volendo si potrebbe anche applicare il processo  al numero 1 che darebbe, però, un ciclo finale ripetitivo:

n = 1

N1 = 4

N2 =2

N3 = 1

e via dicendo.

Se si fa terminare con 1 si ha una fine, altrimenti si raggiunge un ciclo che si ripete all'infinito. Il succo però è lo stesso e ci si chiede: "Questo risultato si ottiene sempre o per numeri sufficientemente alti potrebbe cambiare?". Finora è sempre stato verificato (fino a 5 · 2⁶⁰), ma non se ne può avere la certezza, fintanto che non si trovi una spiegazione dell'andamento sempre convergente o, al limite, si dimostri che è falsa la congettura e che capiti che non si raggiunga mai il numero 1.

Il problema è che la serie di numeri interi che finiscono con uno non dipende apparentemente dal numero di partenza. L'andamento sembra del tutto casuale o quanto meno è "sveltito" di molto solo se il numero di partenza è una potenza di due.

Ad esempio, prendiamo il numero 8192. Applicando il processo descritto da Collatz si hanno sempre numeri interi pari che vengono sempre divisi per due, ossia si hanno le potenze decrescenti:

8192 - 4096 - 2048 - 1024 - 512 - 256 - 128 - 64 - 32 - 16 - 8 -4 - 2 - 1 (- 4 - 2 - 1)

In soli 13 passi si ottiene 1. La faccenda si spiega facilmente dato che 8192 = 2¹³.

Prendiamo, adesso, un numero decisamente più piccolo che, intuitivamente, sembrerebbe dover arrivare a 1 velocemente... nemmeno per sogno!

n = 27

27 - 82 - 41 - 124 - ....... - 16 - 8 - 4 - 2 - 1

Bene calcoliamo pure tutti termini e vedremo che ci vogliono ben 110 passi per arrivare a 1. L'andamento dei numeri successivi è assolutamente imprevedibile. Vediamo in un grafico il caso di 27 (Fig. 1).

In ascissa abbiamo il numero di passi e in ordinata il corrispondente numero della serie. No, non spaventatevi, ma si arriva fino a 9232. L'andamento del tutto imprevedibile si mette nei binari giusti quando, finalmente, si arriva a una potenza di due.

L'irregolarità ancora inspiegata nell'avvicinarsi al fatidico numero 1 è dimostrata molto bene, prendendo, ad esempio, 4 numeri dispari consecutivi: 943, 945, 947, 949. In tutti e quattro i casi sono necessari lo stesso numero di passi, ma l'andamento è decisamente diverso (Fig. 2)!

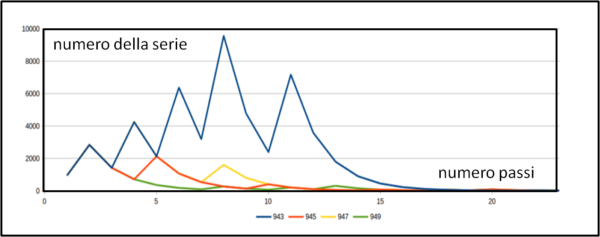
Beh... forza ragazzi, pensateci, magari riuscite voi a risolvere il problema... mai dire mai!