Categorie: Cosmologia
Tags: Big Bang definizione espansione iperbole punto singolarità
Scritto da: Vincenzo Zappalà
Commenti:14
Il Big Bang non è un punto! ***
Questo articolo è una delle tante "ciliegine cosmiche" che potete gustare QUI
Teniamoci forte e cerchiamo di rivisitare con il giusto approccio la classica visione del Big Bang. Direi che il nostro Circolo è pronto per affrontare questa sfida.
Stiamo trattando nel modo più rigoroso possibile la Relatività Generale di Einstein. Più la capiamo e più sembra veramente spiegare il tutto. Tuttavia, anche lei deve cedere di fronte a quelle cose che chiamiamo singolarità. Spesso, ho parlato anch'io di punti singolari per cercare di rendere più semplice una situazione che va al di là della visione normale della fisica. Una descrizione di "comodo", lo ammetto. Verdiamo, allora di affrontare meglio la questione, pronti ad accettare ciò che è ben difficile immaginarsi nella realtà di oggi.
Partiamo dalla lontana e consideriamo una curva molto ben conosciuta, l'iperbole. Scriviamola nella sua forma più classica:
y = 1/x
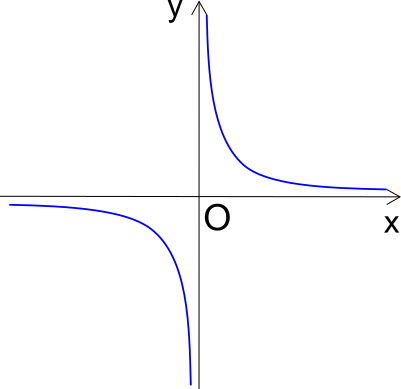
Possiamo dire che esiste un punto con x = 0 che appartiene all'iperbole? No, non esiste, dato che porterebbe a un risultato irraggiungibile. L'unica cosa da fare è inventarsi una rappresentazione matematica che associ a un punto della curva il valore infinito. Nella nostra mente, si forma subito una visione molto pratica e in qualche modo si riesce con il pensiero anche a immaginare quel punto che per quanto ci si avvicini non si può raggiungere mai. Oltretutto, se ci si avvicina a x = 0, provenendo da valori negativi, ci si avvicina sempre più a un punto negativo (meno infinito). Se ci si arriva da valori postivi si naviga, invece, verso più infinito. Due punti che più opposti non possono essere, eppure chi viaggia verso lo zero da sinistra e chi viaggia verso lo zero da destra si sente sempre più vicino all'amico, eppure la loro ordinata si allontana sempre di più. Malgrado tutto ciò, usiamo spesso e volentieri l'iperbole, tanto che ormai non ci rendiamo conto dell'assurdità che stiamo descrivendo... Con le dovute cautele, potremmo anche dire che quel punto ipotetico -e così ballerino- è una singolarità.
Passando allo spaziotempo, anche Einstein si trova nei guai... e quando vorrebbe trattare con la sua teoria così perfetta e ultra confermata l'interno dell'orizzonte degli eventi di un buco nero è costretto ad alzare bandiera bianca e dire che siamo di fronte a una singolarità, cioè non a un punto "strano", ma un concetto che non può essere descritto con la fisica che conosciamo. Se, da un lato, possiamo anche soprassedere su come vive e come si trasforma la materia all'interno dell'orizzonte degli eventi, è molto più importante e stimolante sapere come è nato l'intero nostro Universo.
E qui le cose diventano ancora più complicate e misteriose. Si legge quasi sempre (e, lo ammetto, per comodità divulgativa l'ho fatto anch'io) che tutto nasce da un punto e che, però, quel punto era già il TUTTO. Siamo onesti... già dicendo così, chi non si immagina subito un punto luminoso circondato da tanto buio? Un punto piccolissimo, immerso in... niente, non in uno spazio senza luce.
Situazione veramente assurda, che può essere risolta mentalmente con l'esclusione della parola punto e sostituita con la parola singolarità, ossia un qualcosa che non può essere descritta dalla nostra fisica e nemmeno da quella di Albertino. E' vero che energia e materia si stanno già scambiando i ruoli, ma la relatività generale avrebbe bisogno di parlare nello stesso linguaggio della meccanica quantistica, dato che una avrebbe bisogno dell'altra, ma, ancora, nessuno c'è riuscito.
Ma se non è un punto, che cos'è il Big Bang? Solo e semplicemente una singolarità, così come lo è, fatte le dovute differenze, il punto dell'iperbole che possiede una x uguale a zero.
Peccato, perché l'idea del punto andava benissimo con la odierna sicurezza che l'Universo si espande. Tornando indietro l'espansione vuole dire una continua contrazione di spazio, per cui l'idea del punto sembrerebbe proprio calzante. Essa è oltretutto avvalorata dall'ipotesi dell'inflazione che accelera la corsa a ritroso verso quel punto, che tale non è, ma che è solo un qualcosa che non sappiamo trattare e descrivere perché non abbiamo ancora il linguaggio adatto.
Immaginiamo di non vedere il Bing Bang da "fuori" (cosa oltretutto impossibile!), ma da "dentro". A questo punto (sarebbe meglio dire in queste condizioni, perché la parola punto è diventata pericolosissima...), sappiamo o, almeno, ipotizziamo che le dimensioni di ciò che sarà l'Universo sono appena superiori alla grandezza di Planck, più piccola di qualsiasi cosa di piccolo si possa immaginare. Siamo, però, immersi nel caldo più terribile e nella luce più forte ed energetica possibile.
Cosa succede, allora a un fotone? Ammettiamo pure di accettare che il tempo passi sempre nello stesso modo (d'altra parte facciamo tutti parte dello stesso sistema di riferimento e stiamo, perciò, osservando il tempo proprio, quello che Einstein ci ha dimostrato essere un invariante). Il fotone è costretto a viaggiare alla velocità della luce e quindi è vincolato a percorrere una certa distanza in un secondo. Cosa succederebbe prima dell'inflazione? Lasciatemi dire una cosa molto assurda, ma che potrebbe aiutarci a capire proprio l'assurdità dell'intera faccenda: "Il fotone potrebbe arrivare ai limiti dell'Universo... scontrarsi contro una specie di involucro che lo contiene". No, non può certo essere plausibile dato che l'Universo, per piccolo che sia con il nostro metro, è sempre e soltanto TUTTO ciò che esiste. L'unica possibilità è che l'Universo si espanda con una "velocità" maggiore di quella del fotone.
Capite bene che stiamo cercando di descrivere qualcosa che assomiglia molto alla nostra iperbole. Torniamo ancora a lei e ripetiamo il concetto di base, ancora un volta, estendo la rappresentazione. Più i punti dell'iperbole si allontanano da x = 0 e più il valore della y tende a diventare uno solo (lo zero). Ci riuscirà perfino quando i due punti vagabondi si saranno allontanati fino all'infinito, ossia si saranno allontanati del massimo valore possibile.
Siamo arrivati al dunque... come definire in modo analogo la singolarità chiamata Big Bang? Bene, avevo letto tempo fa una definizione che trovo oltremodo calzante, anche se non facile da digerire (se non ricordo male nel testo La Fisica Cosmologica di J. Peacock). Essa, comunque, rigetta giustamente la definizione di PUNTO, errore da considerare veramente BLU! Ve la riporto con parole mie, ma senza travisarne il significato più profondo e vedrete che assomiglia veramente molto a certe definizioni puramente matematiche.
(1) Prendiamo due "punti" nell'Universo odierno, distanti quanto si voglia, miliardi e miliardi di anni luce, poco importa. Consideriamo, inoltre, un'epsilon piccola a piacere, ossia, in termini fisici, una grandezza piccola quanto si voglia, ad esempio un protone, ma non è vincolante. Ebbene, si può sempre andare indietro nel tempo fino a un momento in cui la distanza tra i due punti era più piccola dell'epsilon, ossia del diametro del protone.
(2) Consideriamo un tempo qualsiasi nella storia dell'Universo e prendiamo una distanza enorme (miliardi e miliardi di anni luce), un gamma grande a piacere, insomma. Ebbene, qualsiasi sia quel tempo, per vicino che sia all'istante iniziale, ossia al Big Bang, esistevano già punti più lontani tra loro della distanza gamma.
Lo so, lo so... sembrano due definizioni contraddittorie, ma in realtà non lo sono e sono le uniche ad avvicinarsi al vero significato della singolarità iniziale. L'unico modo per far scomparire dai nostri occhi un punto luminoso racchiuso in un involucro nero fatto di niente, ma, nel contempo, accettare che l'Universo sia sicuramente finito, ma illimitato, in modo simile a una superficie sferica.
Pensiamoci bene e vedremo che l'espansione dell'Universo, descritta attraverso quelle due affermazioni, è perfettamente plausibile senza alcun bisogno di far nascere tutto da un punto geometrico.
Non per niente, si usano spesso le coordinate comoventi. Utilizzandole si mantiene fissa una distanza nel tempo e quindi si può rappresentare facilmente il Big Bang come una retta infinita nello spaziotempo, ridotto a due dimensioni (spazio e tempo, appunto).
Tu chiamale se vuoi, emozioni...






14 commenti
Caro Enzo vorrei capire meglio la seconda definizione (la prima non mi crea problemi).
(2) Consideriamo una distanza enorme in termini attuali (miliardi e miliardi di anni luce), un gamma grande a piacere, insomma. Ebbene, esisterà un momento nella storia dell'Universo, per vicino che sia all'istante iniziale, ossia al Big Bang, in cui esistevano già punti più lontani tra loro della nostra distanza gamma.
Ammettiamo di essere un fotone. Lui si muove a tavoletta come al solito, ma se si prende una porzione di tempo molto molto piccola (per esempio il Tempo di Planck) il movimento del fotone non è rilevabile, ma il vero problema è che mentre il tempo scorre, un "istante" dopo il Bing Bang l'universo si è espanso ad una velocità maggiore di quella con cui si muove il fotone (inflazione)... è come una rincorsa in cui il fotone cerca di attraversare il nascente universo, ma non riesce a farlo perché questo continua a crescere più di quanto lui possa correre... perciò l'informazione (trasportata dal fotone) impiegherà un tempo enorme o anche infinito per giungere da un punto ad un altro in continuo allontanamento. Ovviamente ciò non vale per tutti i punti, alcuni dopo un certo tempo li può raggiungere, ma altri quelli che ora si trovano ad una distanza gamma a piacere non li poteva raggiungere nemmeno alla nascita dell'universo.
Ho compreso correttamente tale definizione, oppure sono fuori strada?
Paolo
In un certo senso sì, lo spazio era quello che era... tuttavia, conteneva il tutto, e quindi tutto doveva essere compreso in esso. Non poteva esserci un limite che lo contenesse perché niente era fuori di lui. E' un concetto duro, ma le coordinate comoventi possono aiutare a percepirlo dato che portano a descrivere il Big Bang come uno "spazio" illimitato con le linee di Universo parallele tra di loro. Qualsiasi distanza tu consideri in quel momento, esistono cose più distanti.
Nota Bene:
La domanda di Paolo mi ha fatto rileggere con maggiore attenzione la seconda affermazione e, ammetto, che poteva portare a qualche incomprensione. Ho, quindi, cercato di scriverla meglio, in modo da renderla più chiara possibile. Ringrazio Paolo come sempre... Le vostre titubanze o i vostri dubbi sono fondamentali per aiutarmi a scrivere nel modo migliore le idee che vorrei esprimere e che a me sembrano ben comprensibili e, invece, non lo sono per tutti.
Magnifico... il nostro Circolo si basa proprio sulla collaborazione e condivisione sia di certezze che di dubbi! Io faccio il possibile per cercare di aiutare, nel mio piccolo, e voi aiutatemi costantemente esponendo qualsiasi, pur piccola, incomprensione.
Caro Enzo sempre così per trovare conferme. La prima definizione indica "qualcosa" di infinitamente piccolo che però contiene il tutto ossia infiniti punti, per cui per quanto si possono prendere due punti estremamente distanti ci saranno sempre altri punti più distanti ( dato che i punti sono infiniti).
Un pò come per i concetti di infinitamente piccolo e infinitamente grande, quindi quel qualcosa ( singolarità ) è entrambe le cose.
Tra l'altro noi, come il resto dell'universo, siamo comunque all'interno del Bing Bang, ma in un tempo diverso, poichè il Tempo e lo spazio (o meglio lo spaziotempo) sono nati con lui e non erano intorno a lui.
Se mi sto sbagliando correggimi.
In realtà sì, convivono proprio due definizioni normalmente e apparentemente opposte. Dici bene nel dire che facciamo parte e non siamo esterni.
Approfitto del tema affrontato da Enzo, per (ri)proporre due dubbi che ho da tempo.
Mi sono venuti mettendo insieme due affermazioni che ho letto, ormai tempo fa, riguardo le caratteristiche dello spazio fisico dell'Universo:
Da qui i due dubbi ed, implicitamente, le mie conclusioni.
Se l'Universo fosse infinito, deve esserlo stato dall'inizio, diciamo dal Big Bang?
Mi sembra ragionevole assumere che uno spazio finito, per quanto si possa espandere velocemente, non possa diventare infinito (in un tempo finito).
Se fosse così, allora l'immagine di uno spazio fisico dell'Universo di estensione estremamente ridotta nei primi istanti dopo il Big Bang sarebbe sbagliata?
Mi sembra che la risposta affermativa a queste due domande possa essere in questo articolo.
Queste sono quelle domande che rimangono sempre con risposte sospese, proprio per come è definita una singolarità. Probabilmente bisognerebbe cambiare completamente il modo di pensare a riguardo. Infinito e finito sono concetti che possono coesistere, se pensiamo anche solo al fatto che il Big Bang si vedrebbe dappertutto, dato che tutto è nato da lui. Io spesso cerco di vederla così: dato che non esiste il nulla o, quantomeno, non esiste niente che possa confinare l'Universo (come dici tu, le barriere sono assurde) , l'Universo è il tutto e come tale deve essere infinito anche quando e se era confinato in volume infinitesimo. Ma stiamo bene attenti al volume... Ne parlano tutti, ma in realtà se introduciamo la parola volume introduciamo automaticamente un "contenitore" che non può esistere. Lo spazio è un qualcosa che deve sempre essere infinito secondo una certa definizione. Ti dirò a me piace poco la definizione di illimitato, rifacendosi alla sfera. Da un lato si avvicina al concetto, ma dall'altro crea visione distorte. Caso mai è la metrica che lo descrive che può portare a tragitti che si chiudono su se stessi. Sto provando a scrivere qualcosa sulla vera definizione di spazio o ancora meglio spaziotempo, ma una cosa è avere certe idee in testa e un altra è riuscire a spiegarle senza cadere in circuiti chiusi o in antitesi...
Se cerchi di semplificare una certa caratteristica, ecco che rendi un'altra caratteristica confusa o addirittura irrealistica. Ben vengano questo tipo di dubbi e visioni contrastanti. Fanno bene a tutti e sicuramente a me per primo che cerco di estrarre il semplice senza minare a fondo le fondamenta. Sapessi quante definizioni profondamente errate si tirano fuori cercando di semplificare ciò che solo formule matematiche posso definire. Tanto per citarne una che conosciamo molto bene: il lenzuolo con una pietra sopra. Un'immagine che ti fa veder cadere fisicamente gli oggetti verso la massa principale, suggestiva quanto vuoi, ma profondamente errata, dato che è la metrica che in qualche modo si deforma causando quell'effetto.
Ciao Enzone sono tre giorni che mi mordo la lingua o meglio il dito ma non resisto e sono disposto a correre il rischio di una bastonatura. Senza arrivare al big bang sono già in difficoltà con l'iperbole, parlando di fisica e non di matematica "pura" un dubbio mi viene cioè quando il valore della funzione arriva alla lunghezza di Plank il prossimo step è proprio x=0. Ricordo bene Achille e la tartaruga nel tuo corso di math. Se le cose stanno così la curva diventerebbe illimitata ma non infinita, però quando cerco di trarne il significato riferito alla singolarità mi si confonde tutto e buona notte ai suonatori.......
No, caro Frankuccio..., parlando in termini fisici, Achille raggiunge la tartaruga perché non può fare un passo più piccolo di un epsilon. Ma, anche in termini geometrici, basta prolungare le due rette del moto... Il limite è finito! I termini sono infiniti ma il limite è finito.
Nel caso dell'iperbole invece la curva va proprio a infinito, non esiste un limite fisico. D'altra parte l'ipotesi dello spazio di geometria iperbolica è proprio infinito. Se x si avvicina a zero la curva non raggiunge comunque mai un valore finito "stabile".
Temevo questa risposta, non credo poter di arrivare a visualizzarla. Nella mia testa vedo il 10 alla -35 e quando sono li o mi fermo o salto dall'altra parte.
Buonasera,
m'intrometto nel suo bel sito per portare una lettura differente in quanto è evidente che la geometria differenziale riemanniana coi tensori utilizzata da Albert Einstein, ma sopratutto il concetto di tempo, non sono conciliabili con la QM e neppure con la seconda quantizzazione dei 2 Teoremi di Noether.
E' fuor di dubbio che la singolarità non abbia esistenza fisica e che il concetto di asintoto che lei ha usato esiste in geometria analitica solo in virtù dell'ipotesi del continuo esistente in matematica (oggi nota indecidibilità a cui finalmente si sono rassegnati i matematici dopo avere sperato Prometeicamente a lungo che il Teorema di Kurt Godel non avesse ripercussioni profonde sulla stessa matematica).
Parto dalla prima riflessione, l'energia è quantizzata e il campo spaziale è solo uno dei campi quantistici covarianti senza il quale non possono esistere (e viceversa) gli altri campi quantistici covarianti e con questi campi gli eventi con osservabili.
La cosa è dimostrabile quantizzando il secondo Teorema di Noether e scoprendo che la conservazione della carica di una particella è una legge di conservazione impropria, in quanto non è una legge di conservazione generale valida ovunque, ma tipicamente gauge, data dalla interazione dei campi particella, carica, spazio, dove tutti i campi sono necessari all'esistenza della realtà (evento) stessa.
Il tempo ci sta generando problemi di metafisica in fisica fin da Newton e con Einstein non è diverso.
Viene teorizzato (ma senza dimostrarlo) che il tempo è una dimensione, la quarta.
Lo spazio tempo di Minkowski di fatto non esiste ed è Fisica Teorica mai dimostrata ad altissimo rischio di metafisica.
Non a caso l'effetto Unruh (https://it.wikipedia.org/wiki/Effetto_Unruh) dimostra che lo spazio tempo di Minkowski non è idoneo alle osservazioni sperimentali di tale fenomeno.
In termini moderni, il concetto di "vuoto" non è lo stesso di "spazio vuoto", dato che tutto lo spazio è riempito dai campi quantizzati (semplici o complessi come quello di Higgs che è un doppio campo) e che costituiscono l'universo.
Il vuoto è semplicemente lo stato di più bassa energia possibile di questi campi, un concetto molto differente da quello di "spazio vuoto".
Gli stati energetici di qualsiasi campo quantizzato sono definiti dalla Hamiltoniana, basata su condizioni locali, inclusa la coordinata tempo (che non esiste e può essere sostituito con la coordinata distanza).
In accordo con la relatività ristretta due osservatori in moto relativo l'uno rispetto all'altro devono usare differenti coordinate temporali (di distanza).
Se questi osservatori stanno accelerando, potrebbe non esserci un sistema di coordinate condiviso.
In questo caso gli osservatori vedranno differenti stati quantistici e quindi differenti vuoti.
Con questa definizione di spazio vuoto per mettere le basi all'equazione di Temperatura di Unruh, ci spiega anche cos'era lo stato di vuoto primordiale prima che avvenisse una fluttuazione casuale (ovvero a cui non sappiamo dare la causa di generazione) a cui è seguita una rottura spontanea di simmetria che chiamiamo big bang, dove dal vuoto quantistico sopra definito sono apparsi i campi quantistici covarianti in separazione e continua interazione=enucleazione di uno spazio tridimensionale curvo e pieno di energia in radiazione e particelle elementari con una temperatura limite al limite di Planck (come ho letto tra le righe del suo intervento Zappalà).
Solo così il fenomeno di di Unruh trova un significato comprensibile e compiuto risultando incompatibile con lo spazio tempo di Minkowski per cui esso è metafisica.
Il tempo risulta non esistente come dimensione e neppure come oggetto fisico, lo spazio dell'universo è composto solo da 3 dimensioni e geometricamente è un modello (topologico) BF (base fibrato) a 3 dimensioni con omeomorfismi.
Tramite gli omeomorfismi deriviamo i diffeomorfismi in geometria differenziale della RG Einsteniana e ad essa perveniamo.
Il fondo geometrico è una Algebra di Lie o similare sicuramente esotica con meno struttura di quella Einsteniana, ma che poi appare dalle interazioni e retroazioni asinotropiche a basse energie mantenendo covarianze in Langrangiana.
L'analisi a tanto conduce.
La termodinamica che non riusciamo a formalizzare è palesemente legata intimamente al problema della gravità quantistica e la termodinamica è una delle due componenti di quanto chiamiamo tempo.
L'altra componente sono le distanze, il tempo altro non è che le trasformazioni irreversibili del calore avvenute in una massa in moto relativo nello spazio dal punto arbitrario A al punto arbitrario B e non altro.
Dato che nessun oggetto (evento) può essere fermo ma sempre e solo in moto relativo rispetto ad altri oggetti (eventi) in moto relativo, ogni oggetto si muove sempre e compie distanze, il tempo non ci serve, basta il moto inevitabile con le trasformazioni del calore irreversibili (tra l'altro è comprovata la irreversibilità anche in QM con violazione della Teoria CPT non solo su C, P e CP, ma anche su T con esperimento BaBar).
L'anno solare unità di tempo convenzionale arbitraria altro non è che la distanza compiuta dal pianeta sol3 nel fare la sua orbita ellittica con eccentricità (il che non ci fa mai produrre due ellissi identiche di distanza) intorno alla propria stella, a cui si aggiungono tutte le trasformazioni termodinamiche del calore irreversibili.
Tanto vale per il giorno, l'ora, i minuti, i secondi [...] i femtosecondi fino alla distanza di Planck (il tempo di Planck sconsiglio fortemente d'usarlo fintanto che non s'è cambiato significato al concetto e parola tempo).
D'altronde è evidentissimo che l'orologio che portiamo quasi tutti al polso non sta misurano una quarta dimensione, ma solo moto e trasformazioni termodinamiche irreversibili del calore, è complicato vederlo solo perché il linguaggio coi verbi e i loro tempi a cui si aggiungono gli avverbi di tempo, ci rendono il cervello che siamo programmato a non vedere la realtà oggettiva dell'orologio (qui servirebbe una lezione di Van Orman Quine sul guardare il linguaggio e il dal bordo osservativo del linguaggio).
La massima temperatura possibile (temperatura alla rottura di simmetria spontanea con big bang) per i limiti imposti dalla QM è la temperatura dove abbiamo la massima quantità di calore e ordine possibili (Carlo Rovelli la pensa come me da un pezzo).
Ridisegnato il quadretto relativistico in questo modo ci accorgiamo dei falsi problemi dati da una falsa metrica contenente un continuo ipotetico dove la realtà fisica non usa alcun continuo.
Le unità di Planck sono unità costanti universali e non dovute ad alcun sistema (internazionale) di misurazione arbitrario.
E' proprio la realtà fisica che ci da tali costanti universali.
Per l'impossibilità della TOE (teoria del tutto) hanno già dato nell'ordine: Cantor, Skolem, Godel, Carlo Cellucci, Luca Umena, D.R. Hofstadter e senza rendersene conto anche Hilbert e R.Feynman.
Potrei citare altri benemeriti ma lascio l'occasione per il futuro.
Il più prezioso risulta essere D.R. Hofstadter in quanto ci indica che ove la TOE sia una funzione autoreferenziale ricorsiva, per i vincoli costitutivi dati dai 2 Teoremi di Godel sarà sempre impossibile ricostruire la funzione originante se non la si conosce a priori dall'interno dello sviluppo della funzione.
Dall'interno dell'universo (unico luogo di esistenza degli eventi) se lo stesso ha come formalizzazione una funzione ricorsiva è impossibile risalire a tale funzione.
Dato che tale funzione è la rottura spontanea di simmetria che ha fatto comparire il big bang con tutti i campi quantistici covarianti che prima non erano espressi, non producevano eventi e osservabili, allora è impossibile conoscere quella funzione.
Che sia così (autoreferenzialità ricorsiva della materia/energia in meccanica quantistica) ce l'ha indicato R. Feynman in Lectures on Physics tramite il problema insolubile delle bande d'interferenza quando si va a osservare, o non osservare, un singolo quanto emesso da un generatore di fotoni o elettroni e che passa tra due fessure, con la comparsa o meno della bande in relazione a non osservare=ci sono le bande di interferenza=passa contemporaneamente da entrambe le fenditure ed è un onda distribuita nello spazio, osservo, interferisco e non ho interferenza dato che passa da solo una fenditura e ho una particella non un onda, ho la particella da collasso della funzione d'onda.
L'interazione tra quanti chiamata osservazione o misurazione altro non fa che portare al collasso la funzione d'onda e come disse Feynman madre natura ha congegnato la cosa in modo tale che sarà impossibile sapere perché funziona in quel modo.
Per cui ritengo seriamente che il vecchio Einstein avesse ragione quando sosteneva che la QM non è una Teoria completa (il problema dell'incompletezza della QM come accusa di Einstein a Bohr è figlio delle camminate tra Einstein e Godel nei giardini di Princeton dove Godel spiegava a Einstein in problema della incompletezza) e che ha delle variabili nascoste e non è accettabile la versione non realista (scuola di Copenaghen).
Ha sicuramente ragione David Bohm e la sua onda pilota di De Broglie
In subordine se così non fosse (lo metto per pura conoscenza in quanto illumina un ulteriore vincolo, personalmente ritengo corretta la spiegazione precedente), come ci indica Carlo Cellucci, anche ove trovassimo la TOE (ma non possiamo dimostrare ne che esiste, ne che non esiste) non potremo mai sapere che è la TOE, in quanto non saremo mai in grado di poter fare tale dimostrazione.
M'auguro d'avere contribuito almeno un pochino al gioco in corso che si chiama non arrendersi al labirinto invincibile (ovvero il mito di Prometeo si manifesta in chi non si arrende) delle leggi della realtà fisica.
Desidero che la mia posizione in merito sia chiara.
Personalmente invito tutti ad arrendersi al labirinto, il mito di Prometeo va ucciso e bisogna ammettere l'impossibilità arrendendosi ad essa, rifiutando la sfida impossibile, anche perché non farlo ci sta solo danneggiando più di quanto c'è utile.
Che le cose sono in questi termini è quantificabile e anche qualitativamente dimostrabile dalle retroazioni della conoscenza in tecnologia coi danni ambientali così prodotti e insolubili in quanto i primi due principi della termodinamica ci sono contro nel nostro agire e non solo il Teorema di Godel.
Se il mio intervento non è stato gradito me ne farò una ragione.
Post scriptum:
Buchi neri e termodinamica, davvero l'orizzonte degli eventi rappresenta in ogni momento del moto del buco nero solo l'entropia della materia fin li caduta nella curvatura spaziale oltre l'orizzonte degli eventi?
Se così fosse per non crescere senza inghiottire altra materia, le trasformazioni termodinamiche irreversibili del calore all'interno del buco nero cessano, sebbene gli atomi non possano che diventare un brodo di radiazione e particelle elementari e compresse a una pressione limite al massimo della pressione possibile=calore=energia.
Dalle trasformate di Lorentz (RR) sappiamo che gli oggetti s'accorciano in direzione del vettore di moto (sia che sia con, o senza moto rotazionale ulteriore) e il fenomeno diventa significativo e manifesto a velocità relativistiche, coestensivamente il falso tempo rallenta, cosa accade?
Lo spazio di cui sono fatti ampiamente gli atomi/fermioni si contrae in direzione del vettore di moto (gli oggetti si riducono di dimensioni) anche in assenza di accelerazione e le trasformazioni termodinamiche del calore irreversibili rallentano e più sono lente meno entropia producono e più distanza serve perché avvengano le trasformazioni termodinamiche.
Le RR sono asinotropiche e ci sono solo in direzione del vettore di moto.
La RG ci dimostra che osserviamo questa contrazione e rallentamento delle trasformazioni termodinamiche anche dentro a campi gravitazionali.
Per cui la cosa funziona anche nei buchi neri dove le leggi della fisica valgono se non ci sta una singolarità che mi porta nel magico mondo dove le leggi della fisica non valgono.
Quindi essendo impossibile portare fermioni a velocità c, quanto comprimerli in una distanza inferiore a quella di Planck, eppure sono loro che cadono dentro ai buchi neri insieme ai fotoni, le trasformazioni termodinamiche irreversibili del calore non possono cessare completamente neppure in un brodo di fotoni e particelle elementari molto simile al periodo pre inflazione dell'universo, indipendentemente dalla curvatura in cui si trovano.
Così questa crescita dell'entropia deve accadere dentro i buchi neri e la radiazione di Hawking prima che il buco nero raggiunga la temperatura d'evaporazione, evaporando completamente, fa sì che tale radiazione ha il ruolo fondamentale di rendere quell'energia termica irrecuperabile=entropia allo spazio meno curvo al di la dell'orizzonte degli eventi del buco nero, in modo che compensi la mancata crescita dell'orizzonte degli eventi per trasformazioni termodinamiche irreversibili del calore di tutta la radiazione e particelle elementari cadute nello spazio curvo oltre l'orizzonte degli eventi (quindi dentro a tale orrizzonte), in quanto non possono cessare d'esserci per quanto lente e deboli.
Basta eliminare la singolarità metafisica per poter eliminare paradossi e trovare altra conoscenza, idem col tempo.
La gravità quantistica dovrà dare inevitabilmente formalizzazione alla termodinamica perché abbiamo appena visto che curvatura data da gravità influisce sulla termodinamica e le sue trasformazioni energetiche del calore irreversibili cambiandone velocità e quantità d'entropia prodotta per ogni trasformazione, bisogna capire come mai anche il moto relativo degli oggetti in direzione del vettore di moto produca tale effetto.
Ho letto sulla misurazione della piccola curvatura dello spazio effettuata recentemente con satelliti: l'universo in quanto composto solo di campi covarianti quantistici non potrà mai essere infinito, servirebbe energia infinita; com'è evidente la piccola curvatura non ci dice la topologia, ma la non esistenza del tempo e le 3 dimensioni invece di 4, riducono il numero d'ipotesi topologiche e a mio avviso non esiste alcuna preclusione a una violazione del numero barionico e conseguente decadimento del protone con ritorno dell'universo nel tutto dopo una sua morte termica alla fine di una vita termica (Gamow l'universo è un pasto gratis).
Le deboli asinotropie nella radiazione di corpo nero del fondo cosmico, ci indicano la separazione e la loro amplificazione in ulteriori asinotropie da retroazioni di percorso in separazione durante l'espansione, quando da un tutto quantistico al minimo livello d'energia e senza uno spazio enucleato (per cui non un punto non un luogo ma solo uno stato), emerge una rottura di simmetria con moltissima energia separata in valori positivi e negativi producenti eventi quantistici con uno spazio quantistico a sua volta evento quantistico, il tutto in moto con espansione, dove il valore di tutta l'energia presente tende a zero e dove tornerà alla sua morte termica.
La struttura a moti relativi in espansione non ci permette di trovare la direzione sorgente, in quanto non esiste un punto sorgente, ma una direzione sorgente esiste eccome, in quanto siamo in uno spazio topologico tridimensionale con base e fibrato in espansione e le asinotropie, quanto la separazione, dovrebbero darci modifiche delle leggi di conservazione ove trovassimo per puro caso la direzione vettoriale inversa alla sorgente si dovrebbe ridurre l'entropia e veder salire le temperature andando in tale direzione e la ragione è presto detta, nessuna delle simmetrie che troviamo può essere completa, tutte devono rompersi, questa è la separazione con autoreferenzialità, indecidibilità, ricorsività e impossibilità della TOE.
Sommariamente l'universo è una struttura autoreferenziale a rottura di simmetria spontanea producendo separazione, ma il suo valore iniziale e finale è tendente a zero, in quanto zero non può essere tale in QM, il valore minimo dell'energia senza spazio ed eventi quantistici è la cosa più vicina a nulla e tale cosa è il tutto unito, di cui non sapremo mai completamente la struttura.
Se qualcuno di voi crede a Dio è la cosa più vicina a lui che si possa concepire, sapendo di non poterla davvero conoscere a fondo.
Rileggendomi vedo un canto ascendente asintotico, diretto a questo mistero dell'esistenza destinato a restare tale senza alcuna diversa possibilità e la consapevolezza di tal cosa del cantante che sono io.
Grazie e saluti.
caro Massimo,
forse ti sei dimenticato che questo è un sito che vuol divulgare e non cercare di rendere incomprensibili anche le cose più semplici. Ti prego, evita...
Gentilissimo Vincenzo,
desidero regalarle un link: Kurt Goedel: un relativista incompleto (cartesio-episteme.net)
Com'è evidente non sono affatto solo e non sto affatto sproloquiando.
Non è colpa di Massimo indicare che la struttura della realtà è fatta con una complessità mostruosa e mai completamente conoscibile.
Non è colpa di Massimo se le marginali equazioni differenziali a derivate parziali apparse nella fisica sono diventate centrali nella stessa dopo la crisi dell'ultravioletto nella radiazione di corpo nero e siamo arrivati alla geometria diffenziarle di Einstein che non è corretta in quanto non è quantizzata e usa un continuo dove il continuo non può esserci.
Neppure è colpa di Massimo indicare che ha capito quanto ha capito e ancora non è colpa di Massimo indicare che il tempo è un errore percettivo trascinatoci come lo comprendiamo ora fin da Newton ed è tale solo grazie a come Newton stesso lo ha imposto nel metodo scientifico, diventato poi il metodo di formattazione culturale dei cervelli discenti (glielo dico alla Kuhn tra prima di Netwon e dopo Newton parola=etichetta e concetto=insieme tempo hanno una frattura incommesurabile nel significato che ci trasmettiamo nei limiti della teoria dei segnali, il che rende il precedente concetto/significato non traducibile integralmente).
Anche qui, Carlo Rovelli la pensa come me e io come lui ma caro Massimo, forse ti sei dimenticato che questo sito è qui per divulgare.
Apprezzo moltissimo la divulgazione del sito, non sto prendendola in giro e tanto meno scherzando, mi creda.
Divulgare è opera meritoria e non cambierò idea sul tale cosa anche se alcuni potranno usare il sapere=potere per danneggiare altri, lo avrebbero fatto lo stesso con strumenti intellettuali più miseri.
Ho scritto per chi può capire il contenuto e non per chi usa il sito come divulgativo per imparare partendo dalle basi.
Non mi pare che manchi chi può capire, anzi, però non piaccio.
Se non gradito sparisco.
Saluti.
Sì, caro Massimo, evita pure i tuoi commenti... non sono di aiuto per comprendere le basi.