Categorie: Matematica
Tags: ellisse di massima area geometria analitica quiz soluzione tavoletta giapponese
Scritto da: Vincenzo Zappalà
Commenti:7
Soluzione al problema delle tre ellissi (con ciliegina finale di Fabrizio)***
Come annunciato, il problema necessitava di una preparazione al livello delle medie superiori. L'importante era scegliere bene gli assi cartesiani di riferimento e avere un po' di intuito. Come sempre, Fabrizio è riuscito a far sì che i tre fratelli ottenessero il massimo dal terreno avuto in eredità. Inoltre, ha impreziosito la soluzione con una bella animazione molto istruttiva.
La pima cosa da fare è limitare il campo di azione. Le ellissi devono essere uguali tra loro e ne deriva che ognuna di esse deve avere a disposizione un terzo del cerchio di partenza. Questa divisione si fa abbastanza in fretta tracciando tre raggi che sottendano 120° tra di loro (120 · 3 = 360). Due ellissi consecutive devono perciò "toccare" questi raggi, e dovendo essere uguali tra loro, devono essere tangenti a due a due, esattamente nel punto di contatto con il raggio che divide le tre sezioni, come mostrato in Fig.1.
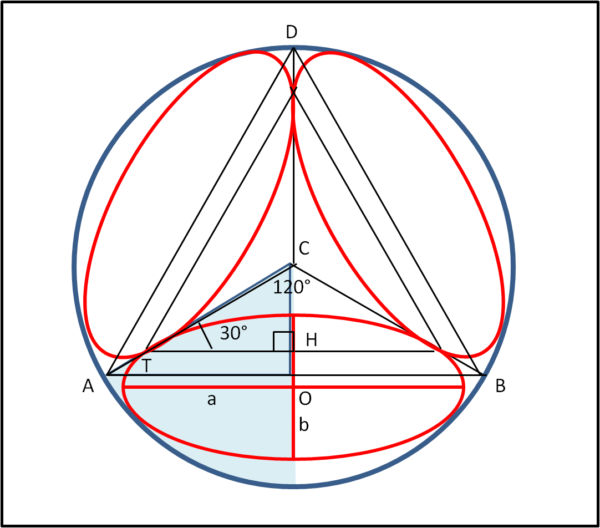
Inoltre, dato che il triangolo ABD è per costruzione equilatero, lo deve essere anche il triangolo che tocca i punti di tangenza delle tre ellissi. Ciò che però più importa è che l'angolo CTH risulta uguale a 30°.
Possiamo allora occuparci di una sola ellisse e, in particolare, della sola parte colorata in azzurro.
Disegniamo la Fig. 2 in cui prendiamo, come origine O degli assi cartesiani x e y, il centro dell'ellissi di semiassi a e b (le nostre incognite finali). Il centro della circonferenza di partenza C ha, perciò, coordinate x = 0 e y = y0
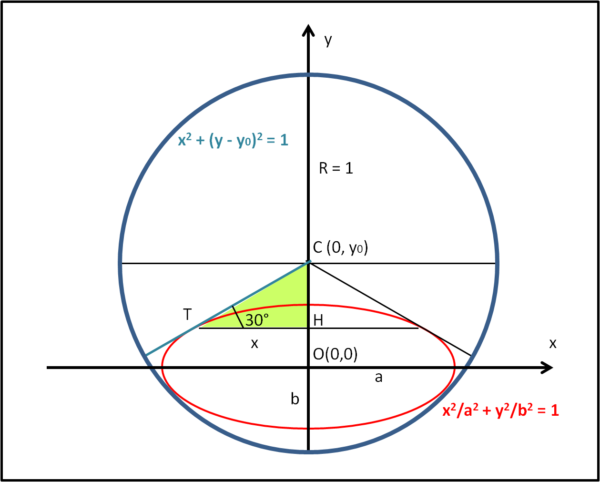
In questo sistema di coordinate l'equazione della circonferenza risulta:
x2 + (y - y0)2 = 1 .... (1)
mentre quella dell'ellissi è:
x2/a2 + y2/b2 = 1 .... (2)
Consideriamo la retta passante per C e per T. Essa ha equazione:
y = tan (30°)x + y0 = x/√3 + y0 .... (3)
Identifichiamo il punto di intersezione di questa retta con l'ellissi (punto di tangenza T). Per farlo basta sostituire il valore di y dato dalla (3) nell'equazione (2)
x2/a2 + (x/√3 + y0 )2/b2 = 1
Svolgiamo un po' di calcoli...
x2/a2 + x2/3b2 + y02/b2+ 2 xy0/√3b2 = 1
moltiplichiamo il tutto per a2b2
x2b2 + a2x2/3 + a2y02 + 2y0a2x/√3 = a2b2
ordiniamola meglio
(b2 + a2/3)x2 + (2a2y0/√3) x + (a2y02 - a2b2) = 0
Questa è una semplice equazione di secondo grado in x, del tipo:
Ax2 + Bx + C = 0
Abbiamo bisogno di risolverla veramente? In realtà no, dato che sappiamo che le sue soluzioni devono coincidere nel punto T di tangenza tra retta e ellissi. Ci basta, perciò, annullare il determinante per ottenere una prima relazione molto importante tra i semiassi e l'ordinata del centro C della circonferenza:
Det. = B2 - 4AC = 0 .... (4)
dove
A = b2 + a2/3
B = 2a2y0/√3
C = a2y02 - a2b2
Andiamo a sostituire nella (4 ) e otteniamo:
4a4y02/3 - 4(b2 + a2/3)(a2y02 - a2b2 ) = 0
4a4y02/3 - 4b2a2y02 + 4b4a2 - 4a4y02/3 + 4 a4b2/3 = 0
- y02 + b2 + a2/3 = 0
y02 = b2 + a2/3 .... (5)
Ovviamente, il valore di y0 dipende sia da a che da b. Ci serve un'altra relazione...
Finora abbiamo sfruttato l'ipotesi che le ellissi siano tangenti tra loro. Abbiamo, però, un'altra caratteristica da sfruttare, ossia quella della tangenza tra ellissi e circonferenza.
Nessun problema, dato che abbiamo già scritto l'equazione della circonferenza (1) e quella dell'ellissi (2). Ci basta, perciò, ricavare x2 dalla (1) e andare ad inserirlo nella (2).
Dalla (1) abbiamo:
x2 = 1 - (y - y0)2
Inserendolo nella (2) si ricava l'equazione:
(1 - (y - y0)2)/a2 + y2/b2 = 1
Moltiplichiamo sia a destra che a sinistra per a2b2
b2 - b2(y - y0)2 + a2y2 = a2b2
b2 - b2y2 + 2b2yyo - b2y02 + a2y2 - a2b2 = 0
(a2 - b2)y2 + 2b2yy0 + b2 - a2b2 - b2yo2 = 0
Scriviamola come:
M y2 + Ny + P = 0
con
M = (a2 - b2)
N = - 2b2y0
P = b2 - a2b2 - b2yo2
Nuovamente, a noi interessa solo porre uguale a zero il discriminante, ossia:
N2 - 4 MP = 0
4b4y02 - 4(a2 - b2)(b2 - a2b2 - b2y02) = 0
b4y02 - (a2b2 - a4b2 - a2b2y02 - b4 + a2b4 + b4y02) = 0
semplificando
a2b2 - a4b2 - a2b2y02 - b4 + a2b4 = 0
Abbiamo solo un termine in cui compare yo, per cui:
a2b2y02 = a2b2 - a4b2 - b4 + a2b4
y02 = 1 - a2 - b2/a2 + b2 .... (6)
Anche in questo caso troviamo un valore di y0 che dipende soltanto da a e da b.
Facendo sistema tra la (5) e la (6) possiamo eliminare la y0 e determinare una semplice relazione tra a e b
b2 + a2/3 = 1 - a2 - b2/a2 + b2
semplifichiamo e otteniamo:
a2/3 = 1 - a2 - b2/a2
Ricaviamo b2 in unzione di a
3b2 = 3a2 - 3a4 - a4
b2 = a2 - 4 a4/3 .... (7)
Possiamo già scrivere quanto vale l'area S dell'ellisse:
S = π a b = π √(a2 b2)
Vogliamo che questo valore sia il massimo possibile. Per come è definita la radice quadrata, essa raggiunge un massimo quando lo fa il radicando. Per cui ci basta trovare il massimo di a2b2
a2b2 = a2 (a2 - 4a4/3)
a2b2 = a4 - 4a6/3
Nessuno spavento ... per il grado, dato che dobbiamo eseguire la derivata di un polinomio. Il valore di a che l'annulla ci dà proprio il valore di a in grado di rendere massima (o minima) l'area.
d(a4 - 4a6/3)/da = 4a3 - 24a5/3 = 4a3 - 8a5 = 0
Mettiamo in evidenza 4a3
4a3(1 - 2a2) = 0
Per rendere uguale a zero questa derivata una possibilità è considerare a = 0, ma questa non è certo una soluzione che ci interessa (è il valore minimo)... L'alternativa è porre:
1 - 2a2 = 0
ossia:
a2 = 1/2
a = 1/√2 .... (8)
che è proprio il valore di a relativo all'ellisse di massima area. La soluzione negativa è ovviamente da scartare.
La (7) ci permette di ricavare b, conoscendo il valore di a:
b2 = a2 - 4 a4/3
b2 = 1/2 - 4/12 = (6 - 4)/12 = 1/6
da cui:
b = 1/√6 .... (9)
Dalla (8) e (9) si ottiene, finalmente, il valore del massimo dell'area dell'ellisse
Smax = π ab = π (1/√2)(1/√6) = π/√12 = π/(2√3)
Smax = π√3/6
I tra fratelli ottengono l'eredità e riescono anche a occupare (tutti e tre) una parte piuttosto grande della superficie totale del cerchio Scer (Scer = π, dato che il raggio è unitario)
3Smax = 3π√3/6 = π√3/2 = 0.87 π = 0.87 Scer
Potremmo dire che è uno strano metodo per determinare il pigreco ...
QUI trovate il quiz
Appendice (con l'aiuto insostitubile di Fabrizio)
Può essere interessante studiare l'evoluzione completa delle ellissi che soddisfano i requisiti del problema: tangenza al cerchio e tangenza tra di loro. Ci è di grande aiuto la Fig.3.
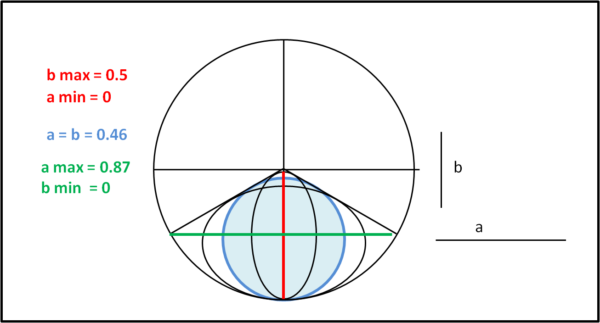
Indipendentemente dalla loro lunghezza si è chiamato b il semiasse verticale e a il semiasse orizzontale. E' facile notare come essi si scambiano i ruoli. Iniziamo con l'ellisse degenere rossa. Essa ha b = 0.5 e a = 0 (ricordiamo , ancora, che il raggio del cerchio di partenza è posto uguale a 1). Schiacciano b e allargando a l'ellissi si ingrandisce pur avendo ancora come semiasse maggiore il semiasse b. Particolare importanza ha il caso in cui a = b = r, ossia l'ellisse diventa un cerchio (azzurro).
Come vedremo tra poco è facile determinare il valore del raggio r, pari a:
r = 0.46
Da quel momento in poi, l'0asse a diventa il semiasse maggiore. Durante questa fase si raggiunge il valore dell'area massima, per poi tornare verso l'ellisse degenere finale in cui b = 0 e a = 0.87 (linea verde). Anche in questo caso è molto facile determinare il valore di a.
Per trovare il raggio r = a = b e il semiasse a finale, utilizziamo la Fig. 4.
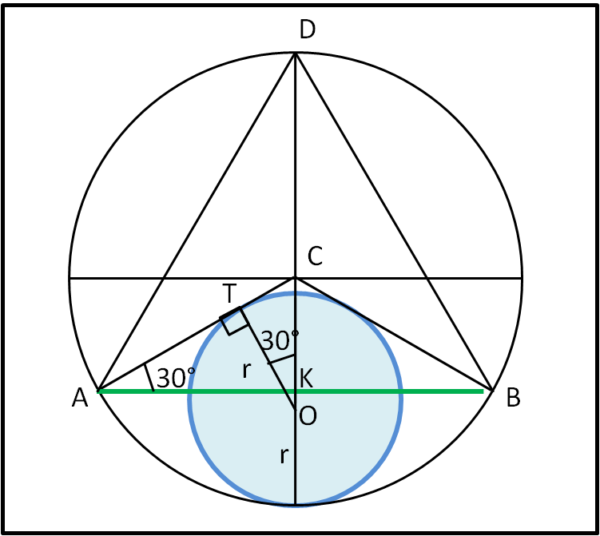
Il triangolo CTO è simile al triangolo CKA, dato che sono rettangoli e inoltre hanno l'angolo in O e quello in A uguali tra loro (quello in O è formato da CO e TO, perpendicolari a CA e KA). Quest'ultimo angolo è, inoltre, per costruzione uguale a 30°.
Possiamo, perciò, stabilire che il segmento CT è pari alla metà di CO. Tuttavia, sappiamo anche che CO = 1 - r.
CT2 = CO2 - OT2 = (CO)2/4
(1 - r)2 - r2 = (1 - r)2/4
4(1 - r)2 - 4r2 = (1 - r)2
3(1 - r)2 - 4r2 = 0
3 + 3r2 - 6r - 4r2 = 0
r2 + 6r - 3 = 0
Da cui r
r = - 3 +/- √(9 + 3) = - 3 +/- 2√3
Scegliamo, ovviamente, la soluzione positiva e abbiamo:
r = - 3 + 2√3 ≅ 0.46
Ancora immediato determinare AK, il semiasse dell'ellissi degenere verde.
Sappiamo che il triangolo equilatero inscritto in un cerchio di raggio R, ha come lato:
l = R√3
Nel nostro caso R = 1 e l =AB. Ne segue:
AK = AB/2 = √3/2 ≅ 0.87
A questo punto, Fabrizio ha completato il tutto con le sue bellissime animazioni di cui ci aveva dato un assaggio già nei commenti: in alto la deformazione delle ellissi (con uno stop nel momento in cui raggiungono l'area massima). In basso, i grafici dell'area delle ellissi e del semiasse verticale in funzione del semiasse orizzontale.







7 commenti
Enzo,
il procedimento che hai indicato, che con qualche differenza (peggiorativa) avevo seguito anche io, pensavo portasse ad identificare tutte le soluzioni compatibili con i due vincoli di tangenza, quello con la circoferenza e quello con la retta.
In realta le espressioni che si ottengono rappresentano correttamente solo le ellissi che hanno due punti di tangenza con la circonferenza. Questa condizione avviene per a>√(3/7).
Per a minore di questo valore si ottengono ellissi diverse da quelle che cerchiamo. Non ho capito ancora il perché.
E' evidente per l'ellisse degenere con a=0 per la quale b dovrebbe essere 1/2, mentre l'espressione
b2 = a2 - 4 a4/3 da 0.
Nella animazione, ho utilizzato queste espressioni per a<=√(3/7): b=1/2-a^2/6 e y0=1/2+a^2/6
Le ho ottenute imponendo la tangenza con la circonferenza nel punto [0,1].
Dubbio legittimo, caro Fabry...
Vedo solo che nella (5) se poniamo a = 0, viene proprio che b = y0. Il che tornerebbe. Dobbiamo pensarci un attimo... sono dietro a uno spezzatino di cinghiale e devo dargli la precedenza
Puff... puff...
tra un assaggio e l'altro, direi che dipende dal fatto che abbiamo escluso a = 0 come soluzione e quindi si porta dietro anche il caso b = y0 e crea discontinuità. In qualche modo, non accetta le soluzioni che abbiano un punto solo di tangenza... dobbiamo pensarci un poco sopra...
Forse ho capito perché le soluzioni con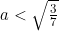 non sono comprese nelle soluzioni trovate con la (5) e la (6).
non sono comprese nelle soluzioni trovate con la (5) e la (6).
Per queste soluzioni il discriminante della equazione in y che abbiamo utilizzato per ottenere la (6) non è nullo. Quindi la (6) non vale.
L'equazione in y ha 2 distinte soluzioni. Una delle quali è sempre y=1 e l'altra ha un valore maggiore di 1, y>1.
Il valore di x quando y=1 è x=0, (o meglio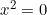 , con le due soluzioni qui coincidenti
, con le due soluzioni qui coincidenti 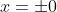 ). Per la soluzione con y>1, x prende due valori immaginari che quindi non corrispondono ad una intersezione tra ellisse e circonferenza.
). Per la soluzione con y>1, x prende due valori immaginari che quindi non corrispondono ad una intersezione tra ellisse e circonferenza.
ero sicuro che avresti capito... e il mio cinghiale è cotto al punto giusto
Poiché per trovare la spegazione ci è voluto un tempo pari a quello necessario alla cottura dello spezzatino di cinghiale, possiamo concludere che il problema era tosto quanto lo spezzatino di cinghiale.
Una nuova unità di misura della complessità dei problemi.
Hai proprio ragione Fabry... potremmo chiamarla CC (cottura cinghiale), ma è già stata usata... Una volta tanto usiamo anche noi un "inglesismo": BC, ossia Boar Cooking. Invece degli asterischi useremo BC, da non confondersi con Before Christ, ovviamente...