La volta scorsa abbiamo descritto un metodo "generale", che sembra quasi prendere in giro gli ingegneri e li giudica piuttosto approssimativi nei loro disegni geometrici o, ancor peggio, incapaci di valutare le approssimazioni (che vengono taciute). Abbiamo anche valutato in modo rigoroso gli errori che si commettono quando viene utilizzato un metodo "generale" che si dimentica delle conclusioni di Gauss.

Nel presente articolo, invece, descriviamo un altro metodo di approssimazione (in questo caso, però, a volte, viene chiaramente detto) in cui non si fa cenno, nelle varie descrizioni che si trovano in rete, delle ragioni della sua applicazione, quasi fosse un dogma da non discutere. Noi, invece, lo proporremo solo dopo aver giustificato la sua applicazione, concludendo con una stima realistica delle approssimazioni derivanti. Un metodo, questo, che io preferisco nettamente e che ci permette di "giocare" in modo non certo difficile con la geometria analitica.

Iniziamo, allora, disegnando una circonferenza di raggio unitario. Lo scopo finale sarà quello di rappresentare qualsiasi poligono regolare inscritto in essa, qualsiasi sia il suo numero di lati. La prima cosa da fare è tracciare il diametro orizzontale e quello verticale, come mostra la Fig. 1.

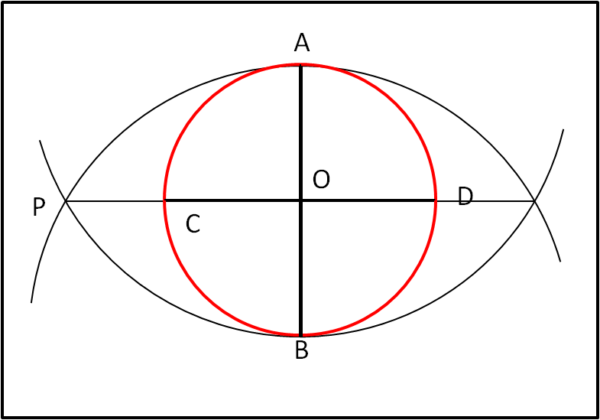
Avendo disegnato il cerchio conosciamo perfettamente il centro O della circonferenza, per cui tracciamo una retta qualsiasi che passi per il centro, determinando un diametro.  Ruotiamo il cerchio e il diametro in modo che quest'ultimo stia in posizione verticale. Facciamo centro nei punti A e B e tracciamo le circonferenze di raggio pari ad AB. Esse si incontrano in P. La retta PO determina immediatamente il diametro orizzontale CD.

Bene, a questo punto, decidiamo di costruire un esagono regolare inscritto (Fig. 2).

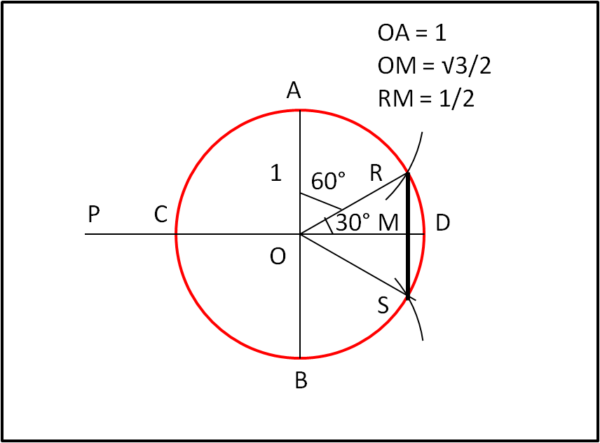
In particolare ci basta scegliere un lato di esso, ad esempio quello perpendicolare al diametro orizzontale. Sappiamo benissimo che il lato dell'esagono inscritto è uguale al raggio del cerchio, per cui ci basta tracciare da A e B le circonferenze di raggio uguale al raggio della circonferenza di base, ossia uguale a 1. Esse incontrano il cerchio di partenza in R e S . Congiungendoli tra loro otteniamo proprio il lato cercato, di cui M è il punto medio che sta, ovviamente, sul diametro CD.

Teniamoci ben stretto il punto P e dedichiamoci al lato dell'esagono RS, anzi, ancora meglio al semi lato RM e alle formule classiche dell'esagono inscritto:

RM = 1/2

OM = √3/2

Il prossimo passo è quello di dividere il diametro AB in SEI parti uguali. Qualche problema? Assolutamente no, dato che Talete ci ha insegnato come poterlo fare.  Come illustrato nel "preambolo" basta tracciare una semiretta qualsiasi che nasca da A, scegliere un segmento a piacere su di essa e con il compasso riportarlo per 6 volte (Fig. 3).

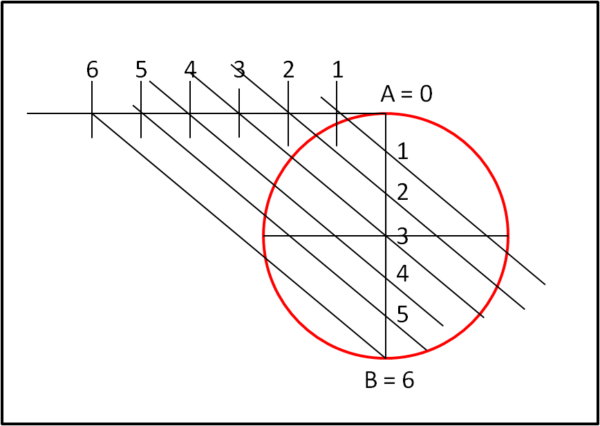
Unendo il punto 6 con B  e poi tracciando le parallele a questo segmento per i vari punti 5, 4, 3, 2, 1 dividiamo esattamente il diametro AB in sei parti uguali. Chiamiamo pure 6, 5, 4, 3, 2, 1, 0 i punti di separazione (6 coincide con B e 0 con A), dato che quelli precedenti possiamo anche eliminarli: ormai sono serviti allo scopo.

Ogni parte in cui è stato diviso il diametro AB avrà una lunghezza pari a 1/3 dato che non è altro che 1/6 moltiplicato per due, che è la lunghezza del diametro. Partendo da A scendiamo di due intervalli. Ci troviamo nel punto 2. Qual è la distanza tra il centro e il punto 2? Beh, molto facile a calcolarsi:

1 - 2 · 2/6 = 1 - 4/6

Con 1 "saliamo" in A e poi con - 4/6 "scendiamo" proprio nel punto 2. Vi sembra un modo molto contorto? Invece no, è molto utile per passare poi a un poligono di n lati. Infatti, il punto 2, dista k dal centro O , data da:

k = 1 - 4/n           .... (1)

A questo punto, in Fig. 4, non ci resta che tracciare la retta che passa per i punti R e 2. Essa interseca il prolungamento del diametro orizzontale in un certo punto P, che è una nostra vecchia conoscenza. Un caso fortunato? No, e lo proviamo subito.

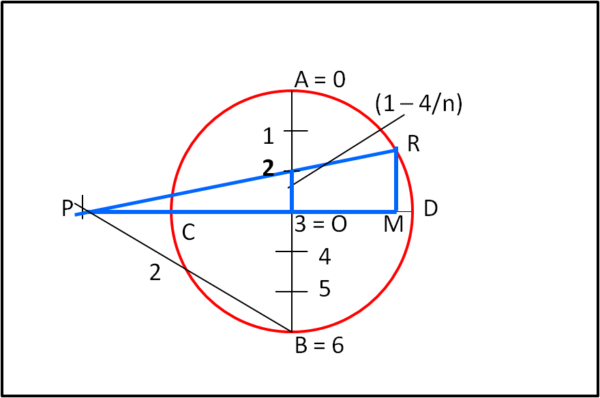
Consideriamo i due triangoli simili RMP e O2P. Dai dati che abbiamo stabilito è facile determinare la distanza PO:

PO/2O = PM/RM

Ma PM vale PO + OM

PO/2O = (PO + OM)/RM

Sappiamo anche, dalla (1), che

2O = 1 - 4/6 = 2/6 = 1/3

mentre

RM = 1/2

e

OM = √3/2

Otteniamo quindi

PO/(1/3) = ((PO + √3)/2)/(1/2)

3 PO =  2(PO + √3/2) = 2 PO + √3

PO = √3

Fermi tutti... Cosa vuol, dire che PO = √3 ?

Facile rispondere, analizzando il triangolo POB. Basta calcolare la distanza PB...

PB =√(OB² + PO²) = √(1² + √3²) = √4

PB = 2

Eh sì, il punto B è proprio quello che ci era servito per tracciare il diametro orizzontale!

Ne segue che possiamo tranquillamente eseguire le operazioni "al contrario": determiniamo il punto P e poi tracciamo la retta che passa per P e per 2 fino a incontrare il cerchio di partenza in R. In tal modo otteniamo il lato dell'esagono, pari alla distanza tra A e R.  Poi si riporta questo segmento con il compasso fino a disegnare l'intero poligono. In questo caso le cose funzionano perfettamente.

Notiamo un altro fatto che ci verrà utile nel proseguo della costruzione: L'angolo al centro O sotteso del lato AR è pari a 60°. Il che vuole dire che l'angolo al centro sotteso dal tratto RD è uguale a 90 - 60° = 30°.

Perché, allora, non ripetere il procedimento per n qualsiasi e vedere di nascosto (noi, però, non ci nascondiamo) l'effetto che fa ?

Graficamente, dopo aver individuato il punto P, il punto 2, che adesso possiamo chiamare anche H, può essere trovato dividendo il diametro AB in n parti uguali, utilizzando Talete, e scendendo di due intervalli da A, ciascuno pari a 2/n. Si traccia poi la retta PH fino a incontrare la circonferenza di partenza. Il punto R così trovato determina, unendolo ad A, il lato del poligono desiderato.

In particolare, ribadiamo che, per n qualsiasi, l'angolo al centro che sottende AR è il complementare di quello al centro che sottende RD. Nel caso dell'esagono Il secondo è la metà del primo, ma in generale no.

Non ci resta che generalizzare la procedura per il calcolo analitico del lato e vedere cosa viene fuori. Facciamoci aiutare da un sistema di assi cartesiani x e y, dove x coincide con il diametro orizzontale e y con quello verticale. L'origine è ovviamente il centro del cerchio di partenza. La Fig. 5 ci illustra il tutto.

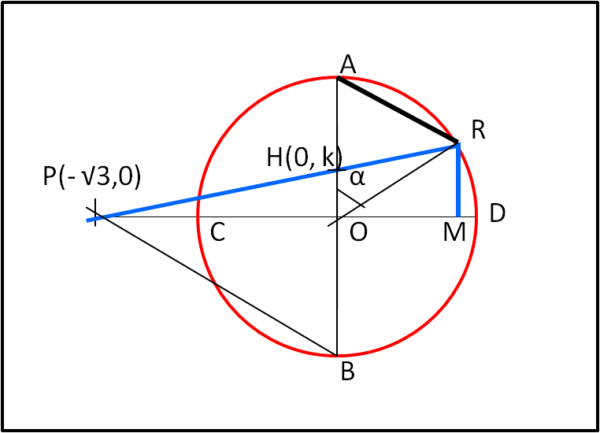
Dobbiamo scrivere l'equazione della retta che passa per i punti P e 2, che adesso possiamo chiamare H, dato che sappiamo come calcolarlo per qualsiasi n attraverso la (1). Essi hanno coordinate:

P ( -√3, 0), H(0, k)

Come si vede, mentre P è quello che è, qualsiasi sia il numero di lati, k (ossia OH) varia in base a n, secondo la (1).

L'equazione della retta che passa per due punti di coordinate (x1, y1) e (x2, y2), è data da:

(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)

Possiamo perciò, nel nostro caso, scrivere, ad esempio (prendendo come punto di coordinate x1 e y1 proprio H):

(x - 0)/(-√3 - 0) = (y - k)/(0  - k)

- x/√3 = - (y - k)/k

ricavando x in funzione di y, si ha:

x = √3 (y - k)/k                 .... (2)

Questa è l'equazione della retta che passa per P e H. Dobbiamo trovare adesso le coordinate (basta la y) del punto R, ossia del punto intersezione tra la retta e la circonferenza di raggio unitario. L'equazione della circonferenza è:

x² + y² = 1

Ci basta perciò sostituire la x con la (2), ottenendo:

3 (y - k)²/k² + y² - 1 = 0

(3y² + 3k² - 6ky)/k² + y² - 1 = 0

moltiplicando tutto per k² si ottiene:

3y² + 3k² - 6ky + k²y² - k² = 0

(3 + k²)y² - 6ky + 2k² = 0

Risolvendo:

y = (3k +/- k√(3 - 2k²))/(3 + k²)           .... (3)

Il valore più grande non è altro che l'ordinata del punto R. Tuttavia, l'ordinata del punto R è anche il seno dell'angolo al centro. Per cui l'arcoseno ci dà proprio il valore dell'angolo al centro che sottende RM. Il suo complementare DEVE essere l'angolo al centro del lato del poligono. Se fosse sempre così la procedura sarebbe perfetta, ma Gauss si arrabbierebbe. Dobbiamo perciò fare come San Tommaso e verificare se questo avviene oppure no e di quanto l'angolo così trovato differisca da quello relativo al poligono regolare.

Per come è stato costruito il tutto, per l'esagono le cose devono essere perfette. Proviamo...

k = 1 - 4/n = 1/3

Andiamo a sostituire nella (3) e risolviamola:

y = (9 +/- 5)/28

Delle due intersezioni con il cerchio dobbiamo considerare quella con y maggiore, ossia quella relativa al segno +. Otteniamo:

y = 14/28 = 1/2

L'angolo che ha per seno 1/2 è 30°. Da cui l'angolo α sotteso da AR risulta proprio (e ci mancava altro...):

α = 90° - 30° = 60°

Proviamo, adesso con il triangolo equilatero. Per lui vale:

k = 1 - 4/3 = - 1/3

e la (3)  ci regala il risultato

y =  (- 9 +/- 5)/28

La y è sempre negativa e dobbiamo scegliere (è l'unico poligono di questo tipo) il valore più negativo, ossia:

y = -1/2

Il che comporta che l'arcoseno sia - 30°, da cui

α = 90 - (-30) = 120°.

Come c'era da aspettarselo, a causa della simmetria rispetto all'asse delle x, anche questa costruzione è perfetta.

Passiamo a n = 4, ossia al quadrato, e qui il gioco è veramente da bambini...

k= 1 - 4/4 = 1 - 1 = 0

Se mettiamo questo valore nella (3) troviamo:

y = 0 +/- 0/3 = 0

L'arcoseno di 0 è 0, ossia il punto R coincide con D. Ne segue che

α = 90 - 0 = 90°

La costruzione è nuovamente perfetta. Non illudiamoci, però... le cose cambiano subito con n = 5 (pentagono)

k = 1 - 4/n = 1/5

Inseriamo questo valore nella (3) e risolviamo...

y = (15 +/- √73)/76

prendendo come al solito il valore più grande

y = (15 + √73)/76 = 0.31

l'arcoseno vale 18.05 e infine:

α = 90 - 18.05 = 71.95

niente male, in fondo, sapendo che l'angolo al centro del pentagono è uguale a 72°.

Non voglio certo continuare nel confronto. Sarebbe bene scrivere un programmino e lasciar fare alle "macchine". Tanto per concludere, possiamo provare con n = 10 che deve avere un angolo al centro di 36°.

Riprendiamo la (3)  con

k = 1 - 4/10 = 6/10 = 3/5

y = (45 +/- 3√57)/84

y =  0.81

l'arcoseno vale 54.10

da cui

α = 9o - 54. 1 = 35.9             ancora niente male!

Voci di corridoio mi dicono che Gauss si sta un po' arrabbiando... Vedete voi di tranquillizzarlo con qualche n abbastanza grande. Mi dà l'idea, però, che questo metodo lavori meglio dell'altro.