Categorie: Matematica
Tags: numero 2 numero più grande parentesi potenze di potenze potenze di potenze di potenze quiz
Scritto da: Vincenzo Zappalà
Commenti:14
(QI) Sappiamo fare le potenze di potenze ? *** (con soluzione)
Un interessante esercizio dedicato alle potenze di potenze...
Abbiamo a disposizione quattro 2, 3 parentesi aperte e 3 chiuse.
Tra tutti i numeri che si possono "costruire", qual è il più grande?
Mentre i numeri 2 sono da usare tutti, le parentesi possono essere anche in numero minore, ma facciamo molta attenzione a loro.
Riassumendo: abbiamo a disposizione
2, 2, 2 e 2
e
(,(,(,),),) come limite massimo.
Prima di cominciare... quante cifre pensate che possa avere il numero finale più grande possibile?
(1) tra 3 e 5 cifre
(2) tra 5 e 10 cifre
(3) tra 10 e 50 cifre,
(4) più di 50 cifre
Buttate giù, senza fare calcoli, la vostra prima impressione e poi sotto a chi tocca!
N.B.: E' vietato usare qualsiasi calcolatrice
Soluzione:
Il nostro bravissimo Andy ha dato la risposta nei suoi accuratissimi commenti. In ogni modo, il risultato è sicuramente inatteso: il numero più grande, corrispondente a 2(2(22)), ossia a due elevato a due elevato alla ventiduesima potenza, supera largamente il milione di cifre. Le parentesi sono importantissime, dato che usandole sapientemente, prima dobbiamo eseguire due alla ventiduesima e poi elevare due a questo numero.






14 commenti
Numeri mostruosamente grandi. Penso a 2 elevato alla 222, ma ancora peggio 2 elevato alla 22 elevato alla 2 cioè 2 elevato alla 484 che supera sicuramente 10 alla 100
fai una tabellina e prova a cercare il numero più grande... non è difficile. Comunque, bravo!
Anch'io, d'istinto e senza fare tanti calcoli, avevo pensato che le parentesi siano inutili e che il numero maggiore sia 2^222. Ma chissà... forse c'è qualche combinazione che mi sfugge. In ogni caso, credo che le cifre del numero maggiore superino di gran lunga le 50.
P.S. per Albertone: Perché dici che (2^22)^2 = 2^484 ? Per le proprietà delle potenze non dovrebbe essere 2^44? Dove sbaglio?
P.P.S. per Albertone: ho capito... prima si eleva 22 alla seconda (484) e poi 2^484, quindi le parentesi servono!
e come se servono!
fate i conti e ne vedrete delle belle!
Perbacco! Quasi 20.000 cifre!20.000 cifre!
Caro Marco,
esegui una ricerca sistematica...
Caro Enzo,
il numero più grande potrebbe (il condizionale è d'obbligo) essere 2^(2^22);
pongo per comodità 2^22 = k, il "numerone" diventa 2^k.
Operando tutto il procedimento senza calcolatrice, per stabilire il valore di 2 alla 22, si può scrivere:
2^22 = 2^10 × 2^10 × 2^2
2^10, ricordando la “tabellina” delle potenze di 2, fa 1024 (se uno non lo ricordasse,
2^10 = 2^5 × 2^5 = 32 × 32 = 1024)
Ma siccome 2^10 × 2^10 = 1024 × 1024 = 1024 × (1000 + 20 + 4) =
= 1024000 + 10240×2 + 4096 = 1 024 000 +
20 480 +
4 096 =
= 1 048 576
quindi 2^10 × 2^10 × 2^2 = 1 048 576 × 4 = 4 194 304 che è il valore di k come posto prima,
per cui 2^22 = 4 194 304 e il “numerone” sarà 2 ^ (4 194 304).
Per stimare tale numero, si può chiedere aiuto ai logaritmi:
ponendo: 2 ^ (4 194 304) = x ovvero
log base 2 di (x) = 4 194 304 che equivale a scrivere (Log (x) ) / (Log(2) ) = 4 194 304
(Log è il logaritmo base 10)
Ponendo Log(2) = y equivale a scrivere 10^y = 2
se y = 1 / 2, cioè √10 (il valore approssimato sostitutivo di pi-greco usato da qualche antico matematico), ovvero 3 e qualcosina siamo ancora lontani dall'identità,
proviamo allora y = 1 / 3 cioè radice cubica di 10; ma se radice cubica di 8 fa 2, radice cubica di 10 fa 2 più qualcosina che è più prossimo all’identità, quindi assumendo come valore approssimativo Log(2) ≈ 1 / 3
si può scrivere: Log(x) / (1 / 3) ≈ 4 194 304,
cioè Log(x) ≈ 4 194 304 / 3 = 1 398 101 (trascurando il resto della divisione).
Ora, per n intero, 10^n da un numero di n + 1 cifre:
10^1 → 2 cifre
10^2 → 3 cifre
10^3 → 4 cifre
10^6 → 7 cifre
10^9 → 10 cifre
allora x sarà un numero con oltre 1 000 000 di cifre e siccome era stato posto
2 ^ (4 194 304) = x ne consegue che 2^(2^22) = 2 ^ (4 194 304) dovrebbe essere un numero composto da oltre 1 000 000 di cifre
Il nostro Andy non perdona! E' difficile che una calcolatrice riesca a dare il risultato voluto!
Caro Enzo,
sempre ammesso che il numero più grande ottenibile in base alle condizioni poste nel quiz sia 2^(2^22),
per ottenere un'approssimazione migliore, senza l'uso della calcolatrice, si potrebbe consultare una tabella dei logaritmi e con una "time machine", trasportarsi temporalmente al periodo intorno al quale visse il grande Nepero.
Da questo link Storia (unige.it) estraggo: "I risultati dello studio di Nepero comparvero nell'opera Mirifici Logarithmorum canonis descriptio eiusque usus in utraque trigonometria, pubblicata nel 1614 a Edimburgo. Le tavole di Nepero ebbero subito un notevole successo e la sua opera fu subito tradotta in inglese. Il matematico Briggs (1556-1630) nel 1615 fece visita a Nepero in Scozia; in quell'incontro essi convennero che sarebbe stato opportuno costruire una tavola dei logaritmi a base dieci. Nepero non ebbe più modo di realizzare questo progetto perché morì nel 1617, mentre Briggs compilò la tavola concordata. Briggs pubblicò una prima opera con il calcolo dei logaritmi dei numeri da 1 a 1000 con 14 cifre decimali e poi un'altra tavola ancora più precisa."
Senza necessità di arrivare alle 14 cifre decimali, da una qualsiasi tavola logaritmica si può leggere che il logaritmo a base 10 di 2 è 0,30103 (sino alla 5a cifra decimale), approssimabile a 0,3 cioè 3 / 10.
Ritornando al post precedente, si può "raffinare" il valore approssimato di 1 /3 stimandolo a 3 / 10
e i 3 / 10 di 4 194 304 valgono 4 194 304 × 3 / 10 = 12 582 912 / 10 =
= 1 258 291 (considerando solo la parte intera)
quindi la ricerca si fa un po' più precisa e 2^(2^22) dovrebbe contenere non meno di 1 258 291 cifre,
ovvero essere non minore di: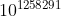
Mentre il nostro Enzo si gode qualche giorno di meritato relax "tanarico",
concludo circa questo interessante quesito con il (molto probabile) numero esatto di cifre della potenza di potenza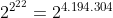
Tale numero è: 1.262.612
Utilizzando esclusivamente gli strumenti a disposizione all'epoca di Nepero, riprendo dal punto in cui
considerando il valore di) sino alla 5a decimale:
sino alla 5a decimale: 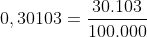
Moltiplico 4.194.304 × (30.000 + 100 + 3) e alla fine divido per 100.000:
4.194.304 × 3 × 10.000 = 12.582.912 × 10.000 = 125.829.120.000
4.194.304 × 100 = 419.430.400
4.194.304 × 3 = 12.582.912
sommo in colonna:
125.829.120.000 +
419.430.400 +
12.582.912 =
126.261.133.312
che diviso per 100.000 fa 1.262.611,33312 ovvero 1.262.611 + 0,,33312
Passando allora dal logaritmo alla potenza di 10 si può scrivere:
approssimando al millesimo 0,33312 ≈ 1 / 3 , l'identità precedente diventa:
dalle tavole delle radici cubiche (che pare fossero già usate dagli antichi matematici babilonesi, greci, cinesi ed indiani) il valore di radice cubica di 10 sino alla terza decimale è 2,154 e allora l'identità precedente diventa:
che scritta in forma "usuale":
Ora, con una moderna calcolatrice avanzata, in grado di calcolare potenze con esponenti a 6 e più cifre, il valore della "famigerata" potenza di potenza è:
La sottile differenza tra 2,154 e 2,065.... è dovuta al fatto che sono state utilizzate solo le prime 5 decimali del logaritmo base 10 di 2, (la parte decimale 0,33312 usata nell'esempio vale qualcosina di meno) ma se all'epoca di Nepero i matematici erano in grado di arrivare alla 14a decimale di un logaritmo, avrebbero trovato un valore del tutto simile a quello calcolato da una calcolatrice odierna avanzata.
In conclusione, Nepero vs. moderne calcolatrici avanzate 1 - 0
Chapeau a Andy!
Grazie Andy Penso che la tua trattazione sia la migliore risposta al quiz