(Q) Ancora sull'età di quattro "individui" ***
Abbiamo preso gusto con l'età delle persone e possiamo continuare considerando quattro scimmie...
Quattro scimmie (a, b, c, d) hanno un'età totale di 63 anni.
Che età ha ciascuna delle 4 scimmie se ab + bc + cd raggiunge il suo massimo valore possibile?
N.B.1: non si può fare uso di derivate o integrali
N.B.2: ovviamente le età sono numeri interi positivi.
N.B.3: il risultato è compatibile con l'età media di alcune scimmie.
La SOLUZIONE la trovate qui






14 commenti
Si può usare la calcolatrice?
Con l’età di 30, 31, 1, 1 = 63 ab + bc + cd = 930+31+1 = 962
con, 16 16 16 15 = 63, 256 256 240 invece =752
Per tentativi, allontanandosi da 30, 31, la somma dovrebbe comunque diminuire.
Parto da lontano, facendo una prova solo con una coppia di valori che sommati danno un numero piccolo dispari, ad esempio
a + b = 7 con f(a, b) = ab
allora le possibili disposizioni sono:
f(6, 1) = 6
f(5, 2) = 10
f(4, 3) = 12
mi fermo qui perché le restanti 3 sono simmetriche alle prime.
Noto che il valore massimo della funzione si ha quando a e b sono circa la metà della loro somma (a = 7 / 2 + 1/2 e b = 7 / 2 - 1 / 2)
Passo allora a 4 valori che sommano sempre 7:
a + b + c + d = 7 con f(a, b, c, d) = ab + bc + cd
dispiegando varie disposizioni:
f(6, 1, 0, 0) = 6
f(5, 2, 0, 0) = 10
f(4, 3, 0, 0) = 12
f(2, 2, 2, 1) = 10
f(3, 2, 1, 1) = 9
f(4, 1, 1, 1) = 6
f(5, 1, 1, 0) = 6
f(4, 2, 1, 0) = 10
f(3, 3, 1, 0) = 12
f(3, 2, 1, 1) = 9
f(3, 1, 2, 1) = 7
probabilmente ve ne sono altre ma mi fermo qui perché, come prima, noto che i valori massimi si hanno quando a e b "girano" intorno alla metà della somma dei 4 valori.
Allora se a + b + c + d = 63 con f(a, b, c, d) = ab + bc + cd
f(32, 31, 0, 0) = 992
f(31, 31, 1, 0) = 992
quindi almeno una scimmietta dovrebbe essere neonata.
Ma come sempre, mi rimane un buon margine di dubbio...
La mia è più una domanda che altro. Se interpreto i tre prodotti come aree di tre rettangoli disposti come segue
https://franic.lima-city.de/varie/4s.jpg
è molto balordo dire che per massimizzare il tutto dovrei minimizzare (b-d)c, cioè avere b=d?
Lo chiedo perché poi, rotolando su questa china, arrivo a massimi MOLTO minori dei numeri dati sopra...
uff, ho messo il link... Ecco l'immagine:
Un po' d'ordine per favore...
Per Gianfranco: niente calcolatrice
Ecco il mio dubbio, perché non ho letto attentamente il testo del quiz nella parte
"N.B.2: ovviamente le età sono numeri interi positivi."
Allora lo zero non va bene (n = 1, 2, 3, ....., n - 1, n), mantengo il ragionamento fatto, allora devo "giostrare"
i valori 30, 31, 1, 1 per ottenere il valore massimo.
Dopo alcuni tentativi, ho notato che una disposizione quasi-simmetrica (nel senso che i valori minimi li ho posti agli estremi destro e sinistro, nel mezzo il valore della metà della somma - 3/2 e il valore della metà della somma - 1/2 anche scambiati di posto)
a = 1 , b = 30 , c = 31 , d = 1
f(a, b , c, d) = ab + bc + cd = 1×30 + 30×31 + 31×1 = 30 + 930 + 31 = 991
e ovviamente
a = 1 , b = 31, c = 30, d = 1
f(a, b , c, d) = ab + bc + cd = 1×31+ 31×30+ 30×1 = 31 + 930 + 30= 991
Con la somma equivalente ad un numero dispari, l'area massima sembrerebbe data dalla formula:
Caro Francesco...... non avevo visto il tuo ultimo commento. Non posso risponderti, ma ci arrivi da solo, dai!
Ecco, allora... continuando a rotolare per la (pericolosa?) china che mi ha portato a concludere che b=d, avrei b=(1/2)*(63-a-c) e devo massimizzare b(a+2c) che scrivo come (sostituendo b e ignorando il fattore di 1/2, ininfluente per la massimizzazione):
a(63-a)+2c(63-c)-3ac.
Ora io non so come massimizzare questo coso, ma con qualche tentativo trovo il massimo (1953) con a=1 e c=31, che implicano b=d=15. Il massimo della funzione richiesta sarebbe quindi 945. Mah.....
...dire che non va, ma io continuo a provare e a sbagliare. Tra l' altro b e d sarebbero 15.5!
caro Francesco,
la tua strada non è sbagliata, ma -forse- dovresti scegliere meglio i rettangoli...
Orpo, come scegliere i rettangoli se non come ab, bc, cd? Ad ogni modo riesco a migliorare quanto sopra usando a=1, c=30, b=d=16, che 'quasi' massimizza a(63-a)+2c(63-c)-3ac ma lascia tutte le età intere e porta ab+bc+cd a 976.
Non credo di poter fare meglio... Attendo lumi :-)
Vediamo se qualcuno riesce a mettere un po' di ordine e poi diamo la soluzione senza "tentativi"...
Probabilmente, una visione geometrica del problema può rendere le cose più chiare:
Se l'area massima è rappresentata dal rettangolo ABCD 31×32 significa che tra i valori di a, b, c, d
a e d sono nulli. Ma siccome a, b, c, d devono essere interi positivi, l'intero positivo più piccolo è 1 e assegnando questo valore ad a e d, i valori di b e c devono "scalare" di un'unità affinché la somma
a + b + c + d = 63
Quindi, dall'area del rettangolo ABCD bisogna sottrarre l'area del quadratino blu 1×1.
Prolungando i lati del quadratino blu all'interno del rettangolo ABCD, la figura complessiva viene divisa in tre rettangoli:
rettangolo verde 1×30
rettangolo rosso 30×31
rettangolo oro 31×1
la somma delle aree da come risultato 991.
Probabilmente si può generalizzare il problema:
se a + b + c + d = S con S intero dispari, calcolando la metà di S e scegliendo i valori interi più prossimi ed equidistanti da S / 2,
l'area massima si ottiene quando
sostituendo nella funzione=ab+bc+cd) i valori sopra determinati, l'area totale max risulterebbe
i valori sopra determinati, l'area totale max risulterebbe 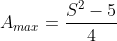
ovvero conoscendo il valore della somma S si possono determinare immediatamente i valori di a, b, c, d e dell'area massima.
Adesso ci siamo! Un bel mix tra Francesco e Andy!