Categorie: Matematica
Tags: asse radicale centro radicale circocentro geometria intersezione tre cerchi intersezione tre sfere ortocentro
Scritto da: Vincenzo Zappalà
Commenti:0
Soluzione dei tre cerchi *** (di Andy, Arturo, Maurizio ed Enzo)
Il problema presentato sembra aver interessato non poco i nostri" matematici" che hanno proposto una serie di dimostrazioni, il più delle volte valide. Invito i lettori curiosi a leggere la lunga serie di commenti al quiz che riportano le soluzioni di Andy, Maurizio e Arturo. Nel presente articolo inseriamo solo quattro dimostrazioni, ossia quella di Enzo, una di Andy, una di Mau e quella tridimensionale di Arturo (al momento solo parziale).
Assi radicali e centro radicale
(di Enzo)
Il metodo utilizzato si basa sulla potenza di un punto (andate a rileggervelo...).
Ricordiamo che la potenza di un punto P rispetto a un cerchio c viene definita come:
Π(P, c) = d2 - r2
dove d è la distanza tra il punto P e il centro del cerchio e r è il raggio del cerchio (Fig. 1).

Ricordiamo anche che se il punto Q sta sulla circonferenza la sua potenza è uguale a zero.
Consideriamo, allora, due cerchi c1 e c2, tali che si intersechino tra loro (ma questo non è un vincolo, come vedremo nell'appendice).
Iniziamo col determinare il luogo dei punti P che abbiano uguale p0tenza rispetto a entrambi i cerchi c1 e c2. Dimostriamo rapidamente che questo luogo di punti è una retta e che, inoltre, è perpendicolare alla congiungente i due centri dei cerchi.
Scriviamo l'espressione della potenza di un punto P rispetto ai due cerchi c1 e c2 e uguagliamole:
Π(P, c1) = Π(P,c2) = d12 - r12 = d22 - r22 .... (1)
Senza perdere in generalità poniamo l'origine degli assi nel centro del cerchio c1 e chiamiamo x l'asse che unisce i centri dei due centri. Essi hanno coordinate O1(0,0) e O2(a,0). P ha coordinate x e y (Fig. 2).
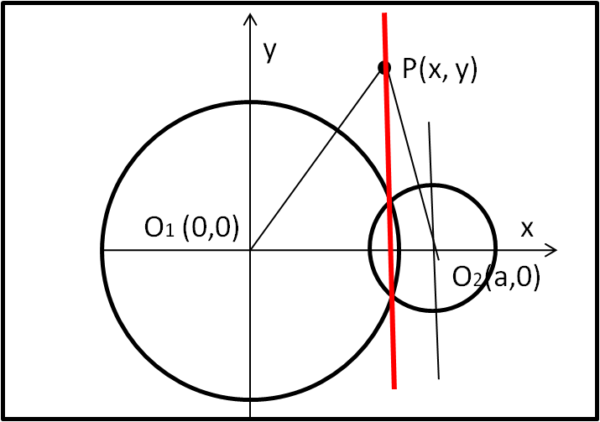
Ne segue che:
d12 = (x - 0)2 + (y - o)2
d22 = (a - x)2 + (y - 0)2
e la (1) diventa.
x2 + y2 - r12 = (a - x)2 + y2 - r22
Non vi è nemmeno bisogno di fare calcoli, anche se elementari...
I termini in x2 e y2 si semplificano mentre quello in y sparisce. In poche parole abbiamo di fronte un'espressione che porta a qualcosa del tipo:
x = costante
Il che implica che il luogo dei punti che hanno la stessa potenza rispetto ai due cerchi non è soltanto una retta, ma è anche perpendicolare alla congiungente i centri dei due cerchi.
Nel caso che i due cerchi si intersechino, questa retta è facilmente tracciabile, dato che i punti di intersezione dei due cerchi hanno potenza zero rispetto a entrambi i cerchi (la potenza di un punto che sta sulla circonferenza è uguale a zero) e quindi il luogo dei punti cercato DEVE passare per quei due punti.
Alla retta, luogo di punti con la stessa potenza rispetto a due cerchi, viene dato il nome di asse radicale e quindi l'asse radicale di c1 e c2 è proprio la retta che passa per le due intersezioni dei cerchi.
Consideriamo, adesso, una nuova circonferenza c3 che intersechi la c2. E' immediato disegnare il suo asse radicale. Questo nuovo asse radicale deve avere un punto di intersezione con quello precedente (se fosse parallelo non saremmo nel caso di tre cerchi intersecantesi vicendevolmente).
Questo punto ha la stessa potenza sia rispetto alla coppia di circonferenze c1 e c2 sia alla coppia c2 e c3. Ne segue che questo punto deve avere anche la stessa potenza rispetto a c1 e c3 (proprietà transitiva: se A = B e B = C, allora A = C). Esiste perciò un punto, detto punto radicale, che ha la stessa potenza rispetto ai tre cerchi ed esso è proprio il punto da noi cercato.
Appendice: Notiamo che l'asse radicale esiste anche per circonferenze che non si toccano (sia internamente che esternamente) e per circonferenze tangenti, come mostra la Fig. 3.

Nel primo caso deve essere sempre e comunque una retta perpendicolare alla congiungente i centri, ma deve anche passare per un punto che abbia i segmenti tangenti alle due circonferenze della stessa lunghezza. Ricordiamo, infatti, che la potenza di un punto è anche uguale al quadrato del segmento tangente a una circonferenza. Nel secondo caso l'asse radicale passa, ovviamente, per il punto di tangenza tra le circonferenze, dove la potenza vale zero per entrambe.
Un triangolo e il suo ortocentro
(di Andy)
L'approccio al caso in questione è di tipo “alla greca”, ovvero utilizza gli elementi di base della geometria euclidea. Date tre circonferenze differenti tra loro, che chiamo C0 , C1 e C 2 , e che si intersecano vicendevolmente come illustrato in Fig. 1:

Traccio tre corde (in rosso) che chiamo x, y, z unenti i punti di intersezione delle suddette circonferenze (Fig. 2):

Vogliamo dimostrare che le tre corde passano contemporaneamente per un unico punto.
Individuati i centri, denominati con O, O’, O’’, delle tre circonferenze, costruisco un triangolo tratteggiato che chiamo △OO’O’’, ottenuto unendo con tre segmenti i già citati centri (Fig. 3):

Le tre corde individuate precedentemente giacciono rispettivamente su tre rette, che prendono il nome di assi radicali, disposti perpendicolarmente ai rispettivi segmenti congiungenti i tre centri (che sono anche i lati del triangolo △OO’O’’). Traccio successivamente le altezze del triangolo (in verde) che chiamo x,’ y’, z’, le quali si incontrano in un punto detto ortocentro, come in Fig. 4:

Essendo, per definizione, le altezze perpendicolari ai lati del triangolo, così come sono perpendicolari gli assi radicali agli stessi lati, allora sia le altezze che gli assi radicali sono rispettivamente paralleli tra loro (ovvero x || x’, y || y’ e z || z’). Posso quindi tracciare infiniti vertici (in blu) su uno qualsiasi degli assi radicali, con i lati paralleli a quelli del triangolo e chiudendo i due lati con un terzo facendo sì che gli altri due vertici si pongano sui 2 restanti assi radicali,
ottenendo così infiniti triangoli simili a quello di riferimento △OO’O’’, come in Fig. 5:

Se, ipotizzando per assurdo che il terzo asse non passi per il punto comune, tracciamo alternativamente una coppia di assi radicali e se le tre coppie passano tutte per lo stesso punto, allora anche il terzo asse radicale deve passare per quel punto (Fig.re 6, 7, 8):



In conclusione, come dimostrato, i tre assi radicali (e di conseguenza le tre corde su di essi giacenti) passano contemporaneamente per lo stesso e unico punto (che è anche l’ortocentro del triangolo disegnato in blu simile a △OO’O’’)
E se fosse il circocentro ?
(di Maurizio)
Questa soluzione può essere considerata una variante di quella di Andy, sfruttando il circocentro al posto dell'ortocentro di un triangolo.
Si tratta del caso limite di intersezione dei cerchi, in cui gli assi radicali sono le tangenti (linee rosse) nei punti di contatto.
Ciascuna tangente è perpendicolare ad un lato del triangolo O1 O2 O3 ( in verde).
Gli assi ( linee nere) dei tre lati si incontrano in un unico punto, il circocentro, ossia il centro del cerchio
circoscritto al triangolo.
Essendo gli assi perpendicolari ai lati, esattamente come lo sono le tangenti, potrò sovrapporre le linee
rosse a quelle nere.
Basta eseguire due traslazioni in direzioni tra loro perpendicolari, come nella figura animata che segue (Fig. 2)

La prima traslazione (verticale) sovrappone la tangente perpendicolare al lato O2 O3 al relativo asse, seguita dalla seconda traslazione (orizzontale) fa scivolare lungo l'asse già sovrapposto le altre due tangenti e le porta a sovrapporsi agli altri due assi.
Completati questi spostamenti possiamo concludere che le tre linee rosse delle tangenti si incontrano tutte e tre in un unico punto (coincidendo con i tre assi del triangolo, individuano il circocentro).
La scelta di tre cerchi a contatto è stata fatta solo per rendere più leggibile il disegno ma tutto il ragionamento vale anche nel caso generico di compenetrazione dei cerchi perché le direzioni dei tre assi radicali restano immutate.
Le tre dimensioni semplificano il tutto
(di Arturo Lorenzo)
Normalmente un problema piano risulta più facile da risolvere rispetto a un problema in tre dimensioni. In questo caso, invece, avviene il contrario...
Immaginiamo di avere due sfere di raggio diverso che si spostano, mantenendo i loro centri su uno stesso piano. Come se fossero bolle di sapone portiamole a incontrarsi e a compenetrarsi l'una con l'altra. Le due sfere (o almeno quello che è ancora visibile) avranno in comune un piano perpendicolare a quello dei loro centri che individua una circonferenza come luogo di contatto delle due sfere. Introduciamo, adesso, una terza sfera che abbia sempre il centro sullo stesso piano delle altre due. Essa inizierà a compenetrarsi con le altre due, formando circonferenze di contatto che devono passare tutte per due punti, la cui congiungente è perpendicolare al piano dei centri.
Non ci resta, adesso, che guardare il tutto "dall'alto", ossia facendo coincidere il piano dei centri con il piano del foglio ed ecco che la proiezione delle tre sfere diventerà esattamente il problema piano iniziale, dove le tre circonferenze di contatto sono ora dei segmenti che hanno un punto in comune, cioè la proiezione della retta che intrerseca le tre circonferenze.
Una semplice figura illustra molto bene la situazione.






