Categorie: Matematica
Tags: geometria luogo di punti quiz triangolo equilatero
Scritto da: Vincenzo Zappalà
Commenti:8
(QI) Un luogo misterioso (NEW: con soluzione tridimensionale)****
Un quiz geometrico un po' più difficile, che si presta anche a generalizzazioni.
All'interno del triangolo equilatero ABC esiste un luogo di punti P (poco conosciuto) tale che:
AP2 + BP2 + CP2 = costante
Qual è e dimostrarlo (senza trigonometria) ***
SOLUZIONE TRIDIMENSIONALE
In un triangolo equilatero ABC consideriamo il suo cerchio inscritto. Esso è tangente ad ogni lato in punti che sono equidistanti dai suoi due vertici. Applicando il teorema di Pitagora risulta subito ovvio che per questi tre punti la somma del quadrati delle distanze dai vertici risulta costante. Il cerchio inscritto sembra proprio essere il luogo che fa al caso nostro. Ovviamente, per poterlo affermare dobbiamo provare la costanza per ogni suo punto.
Ancora una volta un problema piano può risolversi più facilmente in tre dimensioni. Costruiamo la Fig. 1

Senza perdere in generalità disegniamo il piano che contiene il nostro triangolo equilatero ABC in modo che i vertici del triangolo stiano sugli assi cartesiani e abbiano coordinate: A(1,0,0), B(0,1,0) e C(0,0,1). Questo piano ha equazione:
x + y + z = 1 .... (1)
Costruiamo, adesso, la sfera con centro nell'origine che abbia un raggio R tale che essa intersechi il piano precedente proprio secondo il cerchio inscritto nel triangolo. Questa sfera ha equazione:
x2 + y2 + z2= R2 ....(2)
Bene, adesso non ci resta che scrivere la nostra somma di quadrati, considerando un punto P qualsiasi del cerchio inscritto. Il punto P ha coordinate (x,y,z), per cui:
PA2 = (1 - x)2 + y2 + z2 = 1 - 2x + x2 + y2 + z2
PB2 = x2 + (1 - y)2 + z2 = 1 - 2y + x2 + y2 + z2
PC2 = x2 + y2 + (1 - z)2 = 1 - 2z + x2 + y2 + z2
Sommiamo i tre quadrati
PA2 +PB2 + PC2 = 3 - 2(x + y + z) + 3(x2 + y2 + z2)
Ricordando la (1) e la (2), abbiamo:
PA2 +PB2 + PC2 = 3 - 2 + 3R2 = 1 + 3R2 = costante.
Ci accorgiamo, però, che quanto scritto può applicarsi a qualsiasi cerchio che sia concentrico al cerchio inscritto. Infatti, il triangolo rimane lo stesso, mentre cambia il raggio R della sfera. Otteniamo di nuovo una costante dove l'unica cosa che varia è il valore di R.
N.B.: per vedere l'ottimo lavoro di Maurizio vi consiglio di dare un'occhiata ai commenti...






8 commenti
Se i punti del luogo cercati possono essere considerati "interni" anche quando sono sul perimetro del triangolo equilatero, comincerei a considerare i punti di mezzo di ciascun lato come possibili candidati ad appartenere al luogo.
Infatti, data la simmetria del triangolo equilatero, la formula proposta fornirà in tre casi il medesimo risultato.
Il lato del triangolo è "l"
I tre punti mediani sono identificati con M1 M2 M3.
Ne considero uno qualsiasi, ad esempio il punto M2, che dista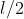 dal vertice B e dal vertice C e dista
dal vertice B e dal vertice C e dista  dal punto A. Applicando la formula otteniamo
dal punto A. Applicando la formula otteniamo 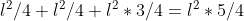 quindi avremmo per la costante il valore
quindi avremmo per la costante il valore 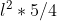 .
.
Sviluppando questa ipotesi vanno cercati altri punti che soddisfino la relazione,ricordando sempre la spiccata simmetria del triangolo equilatero.
Avevo tralasciato la figura ...
Unisco con linee verdi i tre punti sospetti . Attorno a questo piccolo triangolo equilatero si formano altri 3 triangoli equilateri identici.
Ciascuno di essi ha un baricentro che ho indicato con la lettere P e ora verifico se questi punti P hanno distanze dai vertici A B C tali che AP2 + BP2 + CP2 = costante e controllo subito se la costante ha il valore trovato in precedenza :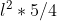 .
.
Considero il punto P più in alto nella figura, quello più vicino al punto C e inizio a calcolare proprio la distanza da C a P
proseguo calcolando la distanza di P da A e da B (sono ambedue alla medesima distanza). Applico il teorema di Pitagora lasciando i quadrati, quindi ottenendo subito i quadrati delle distanze.
=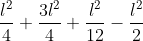
Sommo i tre quadrati delle distanze :
Questo risultato, essendo proprio la costante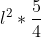 già trovata prima, m i conferma che anche questi tre punti P appartengono al luogo cercato.
già trovata prima, m i conferma che anche questi tre punti P appartengono al luogo cercato.
Ora, osservando la figura, vediamo 6 punti disposti ai vertici di un esagono regolare, tutti ugualmente distanti dal baricentro del triangolo equilatero A B C assegnato all'inizio.
Se i sei punti hanno in comune la distanza dal baricentro viene abbastanza naturale pensare che altri punti, con la stessa distanza dal baricentro, potrebbero appartenere al luogo cercato.
Se così fosse tale luogo sarebbe il cerchio con centro nel baricentro e raggio pari ad un terzo della altezza del triangolo equilatero :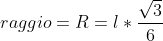
Ma questo deve ancora essere dimostrato.
Fisso il centro del sistema di riferimento XY nel punto O, coincidente con il baricentro del triangolo equilatero assegnato.
Le coordinate di un qualsiasi punto P sono:
Le coordinate dei vertici del triangolo sono le seguenti:
I quadrati delle distanze dai vertici a P sono:
Sommo i tre quadrati e uguaglio la somma a "costante"
Se al posto di costante metto il valore già incontrato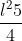 ottengo per il raggio
ottengo per il raggio }) ossia:
ossia:
E se assegnassi un diverso valore alla costante ?
Ad esempio, se dicessi che la costante vale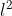 avrei un raggio nullo. In tal caso il luogo dei punti si ridurrebbe al baricentro. Ma è vero che in queste condizioni vale la relazione AP2 + BP2 + CP2 = costante?
avrei un raggio nullo. In tal caso il luogo dei punti si ridurrebbe al baricentro. Ma è vero che in queste condizioni vale la relazione AP2 + BP2 + CP2 = costante?
se sommo i quadrati delle tre distanze dai vertici al baricentro ottengo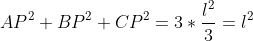
Quindi anche il baricentro , fissando quel valore di costante, fa parte del luogo dei punti cercato.
Ma allora, se vario la costante ...
dal valore minimo =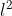 al valore massimo (per restare dentro al triangolo) =
al valore massimo (per restare dentro al triangolo) = 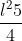 succede che per tutti i valori intermedi della costante ottengo dei cerchi di raggio diverso le cui circonferenze contengono punti appartenenti al luogo cercato.
succede che per tutti i valori intermedi della costante ottengo dei cerchi di raggio diverso le cui circonferenze contengono punti appartenenti al luogo cercato.
Se il ragionamento è corretto, allora il luogo cercato è l'insieme di tutti i punti appartenenti all'area del cerchio inscritto nel triangolo equilatero.
Ciò che posso dire è che esiste un metodo più rapido. Invito Mau, ma anche gli altri a trovarlo...
Un appunto alla conclusione di Mau... Non mi piace tanto il dire:
"il luogo è l'insieme di tutti i punti appartenenti all'area del cerchio inscritto nel triangolo equilatero".
Sembrerebbe che tutti i punti interni al cerchio abbiano la stessa costante, il che non è vero. Trova un modo migliore per dire quello che vuoi dire. Magari Oreste ti può aiutare, dato che è abituato a chiedere: "Per andare dove voglio andare, dove devo andare?"
Secondo Oreste... si potrebbe dire che è l'insieme di tutti i cerchi concentrici, ( dal baricentro ( o incentro ?) al cerchio inscritto) a ciascuno dei quali corrisponde uno specifico valore della costante : dal valore minimo =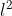 al valore massimo =
al valore massimo = 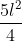
Pare che a Cuneo siano tutti d'accordo
Se assegno tre coordinate nello spazio tali che x = AP, y = BP e z = CP, l'espressione
AP2 + BP2 + CP2 = costante
la posso interpretare come l'insieme di tante sfere concentriche, tipo "cipolla" dove la costante corrisponde al raggio elevato al quadrato =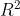
la sfera minima ha raggio = , cioè è proprio il punto che è centro di tutte le altre sfere.
, cioè è proprio il punto che è centro di tutte le altre sfere.
La sfera massima ha raggio = alla distanza dell'incentro dai lati:
che è il raggio del cerchio inscritto nel triangolo equilatero.
Se faccio coincidere l'incentro del triangolo con il centro di questa famiglia di sfere concentriche ottengo come intersezione tutti i centri concentrici in cui è valida la relazione.
A questo punto vi sono vari modi per descrivere l'intera faccenda... ad esempio, considerare un cerchio fisso e allargare il triangolo a dismisura...
Va bene, avete fatto ( tu e Oreste) un ottimo lavoro e la visione tridimensionale aiuta ancora una volta. Io ho seguito una strada leggermente diversa che , a questo punto, posso anche inserire come soluzione, rimandando ai tuoi commenti...
La prossima volta ci mettiamo d'accordo per non "bruciare" subito il quiz
