Soluzione del codice di Fermat ***

26/03/23

Soluzione del codice di Fermat ***

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:6

QUI il quiz

La scoperta del terzo codice è, in fondo, meno difficile di quanto sembri  all'inizio. Oltretutto nel racconto vi è un aiuto "mascherato" che può già far pensare a che strani numeri ci troviamo di fronte. Ho parlato, infatti, di un manoscritto autobiografico e la soluzione si basa proprio sui numeri autobiografici.

Vediamo le caratteristiche peculiari che ci mostrano i primi due codici:

1210

La prima casella si riferisce allo zero, la seconda all'uno, la terza al due e la quarta al quattro. In che modo? La prima casella ci dice quanti zero sono presenti nel numero, la seconda quanti uno sono presenti, la terza quanti due e l'ultima quanti tre. Proviamo a verificare:

0   1    2   3              numero della casella

1    2   1   0

nel numero ci deve essere un solo zero, due uno, un due e nessun tre. Perfetto, il numero si descrive da solo.

Proviamo col secondo.

0  1  2  3  4  5  6        numero della casella

3   2  1  1  0  0  0

Il numero dice che ci sono tre zeri, 2 uno, un due e un tre, nessun 4, 5 e 6

Perfetto!

Il codice con dieci caselle deve essere un numero che ha questa stessa caratteristica.

Però, però... i primi due codici ci dicono anche che la somma delle cifre che compongono il codice è proprio uguale al numero di caselle. Infatti:

1 + 2 + 1 + 0 = 4

3 + 2+  1 + 1 + 0 + 0 + 0 = 7

Ne segue che il nostro codice di dieci cifre deve avere come somma delle sue cifre proprio il numero 10.

Scriviamolo come

 0    1    2     3     4    5    6     7    8    9           numero della casella

n0  n1  n2  n3  n4  n5  n6  n7  n8 n9

Sapendo che:

n0 + n1 + n2 + n3 + n4 + n5 + n6 + n7 + n8 + n9 = 10

La somma è decisamente un numero piccolo, per cui è sicuramente necessario che compaiano molti zeri.

Con queste premesse, molto personali, ho cominciato a mettere tutti zero nelle caselle superiori a zero.

9  0  0  0  0  0  0  0  0  0

Bene, la prima casella mi dice che ci sono nove zeri. Attenzione però, mi dice anche che ci deve essere un uno nella nona casella

9  0  0  0   0   0  0  0  0  1

La somma è proprio 10, ma le cose si complicano, dato che compare un 1. Corro ai ripari e metto un 1 nella casella dell'uno

9   1   0  0  0  0  0  0  0  1

Niente da fare... ho due uno e quindi devo mettere un 2 nella casella dell'uno. Ma questo fatto implica che deve comparire anche un 2 e, quindi, devo mettere un uno nella casella del due.

9   2   1   0   0   0   0   0   0   1

Sono state bloccate la seconda e la terza casella. Ne segue che ovunque vada a mettere il secondo 1 la configurazione della seconda e terza casella non può cambiare. Il che vuol dire che il numero di zeri deve diminuire... al massimo può essere 6.

La soluzione risulta quindi ovvia: basta mettere 6 nella casella dello zero e un uno nella casella del 6.

6   2   1   0   0  0  1  0   0  0

Adesso tutto torna e quindi questo deve essere il codice.

Se volete saperne di più... andate nei commenti del quiz, dove Andy e Maurizio si sono scatenati!

Articoli correlati

6 commenti

  1. Maurizio Bernardi
    27/03/2023 at 00:52

    solo come curiosità,  mi sono scritto i numeri a partire dal 3211000  fino al 6210001000 in sequenza.

    BASE     NUMERO autobiografico / descrittivo nella sua base

       7                3211000

      8               42101000

      9               521001000

     A               6210001000       

    Osservando la struttura di questi numeri autodescrittivi dalla base 7 alla 10 (che indico con A) si vede uno schema che si ripete con regolarità.

    - Ciascun numero ha nella prima posizione un valore incrementato di 1 rispetto al precedente.

    - Tutti i numeri finiscono con 1000

    - La stringa di '0' inclusa tra i due '1' si incrementa di una posizione rispetto al numero precedente.

    Posso facilmente estendere alle basi successive, (per  esempio le prossime 3) questa struttura generando i numeri in sequenza 

    BASE    NUMERO autobiografico / descrittivo nella sua base

    B      72100001000
    C      821000001000
    D     9210000001000

    Ma posso anche non fare riferimento al numero precedente e scrivere direttamente il numero in funzione della sua base.

     -    In prima posizione metto (base - 4)

     -   seguono 2 e 1 nelle due posizioni successive.

     -   poi la stringa di 0  costituita da (base-7)  elementi

     -   concludo con la stringa 1000

    Posso scrivere immediatamente, per esempio, l'autodescrittivo nella base 13 ( ossia D)

    13-4      fissi      stringa di 13-7= 6 '0'      1000 finale

     9      2 1      0 0 0 0 0 0       1 0 0 0

    Per la base 16 (di particolare interesse in informatica) l'autodescrittivo vale

    16-4      fissi      stringa di 16-7= 9  '0'                1000 finale

    C       2 1    0 0 0 0 0 0 0 0 0     1 0 0 0

  2. Andy
    27/03/2023 at 19:19

    Interessante la tua osservazione Maurizio, anche perché da spunto ad alcune riflessioni:

    rimanendo nel sistema a base 10 e applicando il criterio da te descritto, partendo dal codice a 10 cifre

    6 2  1 0 0 0  1 0 0 0  posso ottenere quello da 9 cifre scalando di un'unità il primo numero della sequenza (il 6 in blu), lasciando fisso il 2 ed eliminando uno zero subito dopo il primo 1 (terzo numero da sinistra): 5 2  1 0 0  1 0 0 0

    stesso discorso per 8 cifre:  4 2  1 0  1 0 0 0

    e per 7 cifre:  3 2  1  1 0 0 0

    Praticamente le cifre variano secondo una parte semi-fissa (la prima cifra che diminuisce/aumenta di 1 unità e la seconda cifra che rimane costantemente 2. La parte "binaria" del codice, invece, varia secondo un certo algoritmo:

    nel codice a 7 cifre, la parte binaria è: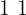 \large 1 \1 \0 \0 \0  che equivale a 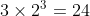3 \times 2^3 = 24 decimale,

    nel codice a 8 cifre è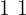 \large 1 \0 \1 \0 \0 \0  che equivale a  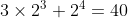3 \times 2^3 + 2^4 = 40 decimale

    nel codice a 9 cifre è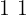 \large 1 \0 \0 \1 \0 \0 \0  che equivale 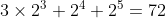3 \times 2^3 + 2^4 + 2^5 = 72 decimale

    e infine per il codice a 10 cifre: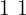 \large 1 \0 \0 \0 \1 \0 \0 \0  che equivale a 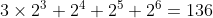3 \times 2^3 + 2^4 + 2^5 + 2^6 = 136 decimale

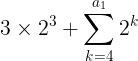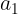    cioè la parte variabile decimale varia secondo l'algoritmo \large 3 \times 2^3 + \sum_{k=4}^{a_1} 2^k  dove \large a_1 è la prima cifra della sequenza. Questo fino alle 7 cifre perché per codici di lunghezza 6, 3, 2 non ho trovato il corrispondente autodescrittivo, mentre per lunghezza 4 e 5:

     

    Cambiando invece la base del sistema di numerazione (base 10, base 11, etc...) e considerando il codice di massima lunghezza relativamente al sistema di numerazione (10 cifre base 10, 11 cifre base 11, etc...) il ragionamento rimane lo stesso ma cambia l'algoritmo di determinazione della parte che si fa variare:

    Insomma, abbiamo detto le stesse cose, tu parlando in "decimalese" ed "esadecimalese" forbito, io in un misto dialettale di "binariese algoritmico" con accento "decimalese"... :mrgreen:

  3. Andy
    27/03/2023 at 19:26

    Le formule si sono "mangiate" i binari del sistema a base 10:
    7      3 2          24DEC = 3×23                                                    1 1 0 0 0
    8      4 2          40DEC = 3×23 + 24                                                 1 0 1 0 0 0
    9      5 2          72DEC = 3×23 + 24 + 25                         1 0 0 1 0 0 0
    10   6 2     136DEC = 3×23 + 24 + 25 + 26                  1 0 0 0 1 0 0 0
     

  4. Andy
    27/03/2023 at 19:28

    Vabbè, anche le potenze del 2 :evil:

    Comunque ci siamo capiti...

  5. Maurizio Bernardi
    28/03/2023 at 01:38

    Molto interessante anche  questa  integrazione. Ottimo.

    Gli autodescrittivi delle basi 2 e 3 non esistono come si può verificare anche esaustivamente date le pochissime configurazioni possibili in queste basi.

    Per la base 6 sconsiglio l'analisi esaustiva delle configurazioni      ma facendo qualche ragionamento si capisce che non ha autodescrittivi.

    Ho fatto un po' di prove in excel e ho visto che  si riesce a generarli in sequenza , a partire da quello di 7 cifre con questa formula.

    N i +1 = (Ni *10) + 10ni - 9000

    in cui N i +1 è il nuovo numero  in base ni+1

    Ni è il precedente numero  in base ni

    Certo che poi non vedo cosa potremmo farcene di uno sterminio di questi numeri, salvo usarli per proteggere la famosa prova perduta del teorema Fermat

  6. Maurizio Bernardi
    28/03/2023 at 01:51

     

    Latex latex ....

    La formula è questa:

    N_{i+1}=(N_{i}*10)+ 10^{n_{i}^{}}  -  9000

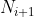    dove        N_{i+1}   è il nuovo numero in base  n_{i+1}

    N_{i}       è il precedente numero in base   n_{i}

     

     

     

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.