Categorie: Matematica
Tags: geometria posizione migliore quadro quiz
Scritto da: Vincenzo Zappalà
Commenti:3
(Q) Come ammirare un quadro **
Entriamo in un museo e cerchiamo di ammirare al meglio il nostro quadro preferito.
Il problema non è certo difficile, ma per la sua soluzione (rapida) ci vuole un po' di fantasia e di conoscenze geometriche di base.
Siamo entrati nella sala di un museo in cui vi è un vero capolavoro che dobbiamo assolutamente vedere. Purtroppo, è posto piuttosto in alto sulla parete e dobbiamo trovare la posizione migliore per ammirarlo. La situazione è quella illustrata nella Fig. 1.
Il nostro occhio P è a un'altezza h dal pavimento, mentre il quadro è sospeso alla parete a un'altezza pari ad a > h. L'altezza del quadro è b. Come già detto anche (a - b) > h. Noi ci poniamo di fronte al quadro e ci spostiamo su un piano verticale che passa per il punto medio orizzontale del quadro.
Quale sarà la posizione migliore del nostro occhio P, in funzione di a, b ed h?
E' obbligatorio usare solo la pura geometria, niente algebra, coordinate cartesiane e trigonometria.
P.S.: Chi ha studiato e risolto questo problema non avrebbe potuto applicarlo alla Gioconda, in quanto non era ancora stata dipinta...
QUI la soluzione
3 commenti
Il nocciolo della questione sembra collocarsi sull'angolo di visuale formato dal punto in cui si trova l'occhio dell'osservatore e le distanze di tale punto dal margine inferiore e superiore del quadro, come evidenziato in questa figura tridimensionale:
Man mano che il punto di osservazione viaggia in un verso o nell'altro sulla semiretta posta ad altezza h, rispetto ad un ipotetico punto di visione ottimale, le distanze dai margini inferiore e superiore del quadro si "stirano", comprimendo lo spazio occupato dall'angolo di visuale:
In realtà dovrebbero esistere infiniti angoli di ampiezza ∠APB, ma il cui vertice P non è collocato sulla retta s:
relativamente alla figura, immaginiamo una circonferenza di raggio R = a - h - b/2 dove tutti gli angoli alla circonferenza che insistono sull'arco AB sono uguali tra loro.
Allora costruendo tale circonferenza passante per i punti A, B, e il punto di tangenza P con la semiretta s, si può ottenere la seguente figura, dove ho inserito dei valori numerici per svolgere i calcoli:
La dimostrazione si può dare osservando questa ulteriore figura:
Considerando il punto di osservazione P’’:
gli angoli ∠APB e ∠ACB sono uguali perché insistono sullo stesso arco AB.
L'angolo ∠ACB è un angolo esterno al triangolo CAP'’ quindi è uguale alla somma dei suoi angoli interni ∠CAP’’ e ∠CP'’A.
Ma poiché ∠ACB = ∠APB, si ha che l'angolo ∠CP'’A = ∠BP’’A deve essere più piccolo di ∠APB:
∠APB = ∠ACB = ∠CAP'’ + ∠CP'’A → ∠ACB - ∠CP'’A = ∠CAP'' > zero → ∠APB maggiore di ∠AP''B.
Stesso discorso se si considera il punto di osservazione P’.
Grande Andy! Sei sempre il migliore
L'unica differenza è che io ho calcolato la distanza con il teorema tangente-secante...
Grazie caro Enzo...
In effetti la soluzione pitagorica e la soluzione tangente-secante si equivalgono:
secondo la soluzione pitagorica, la distanza ottimale è^2&space;-&space;(b/2)^2})
(1)
Considerando il polinomio sotto radice della (1) e sviluppando:
Ora,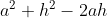
è il quadrato di (a - h) mentre -ab + bh, mettendo in evidenza -b, diventa -b(a - h),
per cui la (2) si può scrivere come:^2&space;-b&space;(&space;a&space;-&space;h&space;))
; mettendo in evidenza (a - h) si otterrà:
(a - h)⋅(a - h - b).
Ma (a - h) è il segmento con origine l’intersezione tra l’asse verticale della parete con l’asse orizzontale dell’occhio dell’osservatore, e secante la circonferenza;
(a - b - h) è la parte “esterna” del segmento secante, mentre d è il segmento tangente alla circonferenza e che parte dalla stessa origine di prima, quindi per il teorema della secante e della tangente:
Sarà banale ma il perché è necessario costruire la circonferenza per trovare il punto ottimale è presto detto:
Il segmento AB si può vedere come la corda contenuta da una famiglia di circonferenze: allora se traccio l’asse di AB, che giace sulla retta u, tale asse transiterà per tutti i centri della famiglia di circonferenze.
Ma sarà una singola circonferenza ad avere in comune un solo punto con la retta s.
In altre parole esiste un solo punto che appartiene contemporaneamente sia alla circonferenza che alla retta s, che è proprio il punto di tangenza P.
Se con un compasso si fa centro in A o in B con apertura pari ad O’M = a – h – b/2 e si segna un arco sulla retta u, si intercetta il punto Q che è quindi il centro della circonferenza specifica.
La proiezione di Q sulla retta s è il punto P, il segmento QP è uguale alla distanza tra u ed s,
che a sua volta è uguale ad: a – h – b/2 , che sarà allora pari alla misura del raggio R.
La proiezione sulla retta s del centro di qualunque altra circonferenza di raggio differente da a – h – b/2, e che contiene la corda AB, ricadrebbe più avanti o più indietro rispetto al punto P.