Categorie: Matematica
Tags: cerchio mistilineo geometria incentro quiz soluzione
Scritto da: Vincenzo Zappalà
Commenti:14
Soluzione del quiz diabolico *****
Premettiamo, ancora una volta, che il cerchio mistilineo è un dato del problema e ha solo le caratteristiche di essere tangente ai lati del triangolo e al cerchio circoscritto. Poco deve importare la sua costruzione. Che AM sia la bisettrice e tutto quello che segue sono cose da dover dimostrare. In realtà, quando si presenta un triangolo e il suo circocentro, nessuno si sogna di chiedere come si fa a costruirlo. Si sa che c'è e lo si disegna. La stessa cosa va fatta per un cerchio un po' strano che, però sicuramente esiste ed è unico per ogni vertice del triangolo.
Ricominciamo dall'inizio e vediamo bene quali sono i dati del problema attraverso la solita Fig. 1
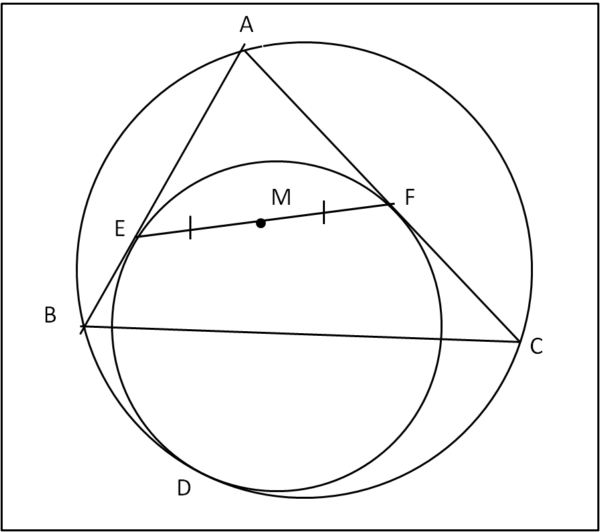
Tutto ciò che sappiamo è che il cerchio più piccolo è tangente ai lati del triangolo e al cerchio circoscritto. Né per il cerchio circoscritto né per quello più piccolo è necessario spiegare la costruzione. A questo punto tracciamo il segmento EF che unisce i due punti di tangenza sui lati e indichiamo il punto di mezzo con M. Con solo queste sicurezze iniziali dobbiamo dimostrare che il punto M si trova sulla bisettrice di BAC ed è l'incentro, ossia il centro del cerchio inscritto al triangolo.
Ovviamente, dato che la dimostrazione esiste, bisogna stare molto attenti alle conclusioni che si traggono dalla figura. Certe caratteristiche sono ben evidenti, ma una cosa è vederle e un'altra è dimostrarle. Se noi disegnassimo il cerchio inscritto, ad esempio, concluderemmo "visivamente" che M è proprio l'incentro. L'apparenza non deve bastare e bisogna verificarla con passaggi logici e dimostrabili.
Possiamo iniziare , sapendo molto bene quali sono gli unici dati che conosciamo e che cosa vogliamo dimostrare.
Come era già successo per il quiz precedente (QUI) è necessario trovare una qualche relazione semplice che caratterizzi l'incentro di un triangolo.
Dedichiamoci, quindi, a studiare le sue caratteristiche .
Utilizziamo la Fig. 2, dove riportiamo un triangolo qualsiasi (niente ha a che vedere con il nostro triangolo ABC del quiz) e cerchiamo di trovare una relazione che possa essere quella da dimostrare per avere la certezza che il punto M sia proprio l'incentro.
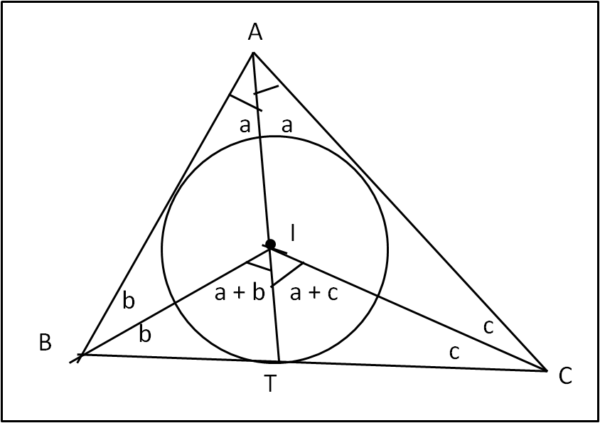
Ricordiamo che l’incentro di un triangolo è il punto d’incontro delle sue bisettrici. Prolunghiamo la bisettrice dell’angolo BAC fino a incontrare BC in T. Consideriamo il triangolo ABI. Se I è l’incentro, possiamo scrivere:
BIT = a + b (angolo esterno del triangolo ABI)
E, analogamente
TIC = a + c
Sappiamo, però, che la somma degli angoli interni di un triangolo è 180° Ne segue che la metà dei loro angoli è uguale a 90°, ossia:
2a + 2b + 2c = 180°
a + b + c = 90°
L’angolo BIC è dato dalla somma di BIT e TIC, per cui:
BIC = (a + b) + (a + c)
BIC = a + (a + b + c)
BIC = a + 90° .... (1)
Possiamo perciò stabilire che l’incentro I è l’unico punto della bisettrice AT tale che l’angolo BIC sia uguale a 90 + a.
Se dimostriamo che la relazione (1) vale per un certo punto M della bisettrice AT, possiamo concludere che M coincide con l‘incentro.
Notiamo un fatto che sarà molto importante: l’incentro I è caratterizzato in modo univoco solo dall’angolo a.
Ritorniamo al nostro problema di Fig. 1, sapendo che dobbiamo iniziare a dimostrare che M sta sulla bisettrice di BAC.
Questa dimostrazione è veramente facile (Fig. 3)
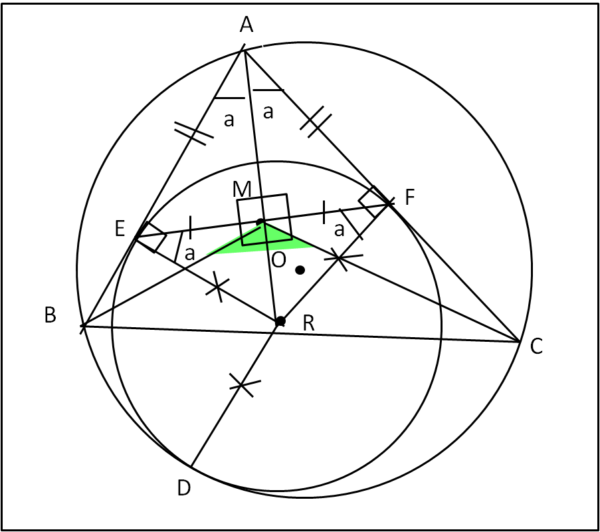
AE = EF
in quanto tangenti al cerchio di centro R, tracciate da un punto esterno.
Ne segue che AEF è un triangolo isoscele e quindi:
AEM = AFM
Sappiamo che EM = EF per costruzione, per cui il triangolo AEM è congruente al triangolo AEF, avendo tre lati uguali.
Ne segue che AME = AMF = 90°, ma soprattutto che
EAR = MAF = a
La retta AM è la bisettrice del l'angolo BAC e passa anche per R, dato che RE = RF (raggi del cerchio mistilineo).
Nella stessa Fig. 3 possiamo notare che AEM = 90 - a, ma sappiamo anche che AER = 90° per cui:
MER = 90 - AEM = 90 - (90 - a) = a
Consideriamo i triangoli rettangoli AER e MER. Essi sono simili in quanto hanno EAR = MER. Ne segue che possiamo scrivere l'uguaglianza tra i rapporti dei loro lati:
AR/ER = ER/MR
ER2 = AR MR
ma ER = RD
per cui:
RD2 = AR · MR .... (2)
Teniamo da parte questa relazione
A questo punto resta da dimostrare che l'angolo verde BMC è proprio uguale ad a + 90. E qui le cose si complicano.
Tracciamo, allora, qualche segmento in più, ottenendo la Fig. 4
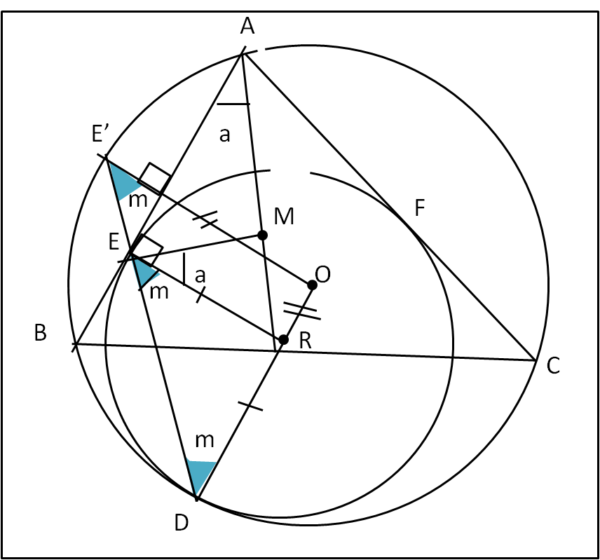
O sia il centro del cerchio circoscritto e R il centro del cerchio tangente ad esso e ai lati AB e AC. D, E ed F sono i punti di tangenza. I due cerchi sono tangenti in D e, quindi, la congiungente OD deve passare anche per R.
Attenzione, adesso, alla parte che segue: qualcosa che sembrerebbe visivamente ovvia deve essere dimostrata adeguatamente.
Prolunghiamo DE fino a E’. Costruiamo, perciò il segmento E’D che passa per E. Dove stia, però, E’ non lo sappiamo ancora.
Tracciamo la perpendicolare da O al lato AB, fino al punto E’, e la congiungente R con E che è, per costruzione, perpendicolare ad AB. Ne segue che E’O è parallela a ER, dato che sono entrambi perpendicolari alla stessa retta AB.
Consideriamo il triangolo ERD. Esso è isoscele in quando i lati ER e DR sono raggi del cerchio di centro R. Ne segue l’uguaglianza dei due angoli m. Il segmento EE’ è allineato con ED per costruzione e, quindi, gli angoli EE’O e DEO sono uguali, essendo E’O parallela a ER. Ma, allora, anche il triangolo E’OD è isoscele (angoli uguali), ossia
E’O = OD.
Ne segue che:
E’ deve stare sul cerchio circoscritto ad ABC.
In Fig. 5, ripetiamo la stessa costruzione relativamente ad F.
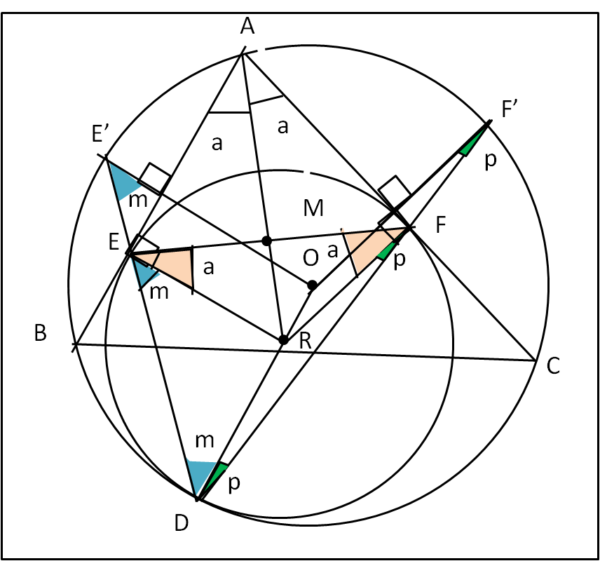
Ricaviamo l'uguaglianza dei tre angoli verdi (p).
Passiamo alla Fig. 6, dove evidenziamo un nuovo triangolo, EFD...
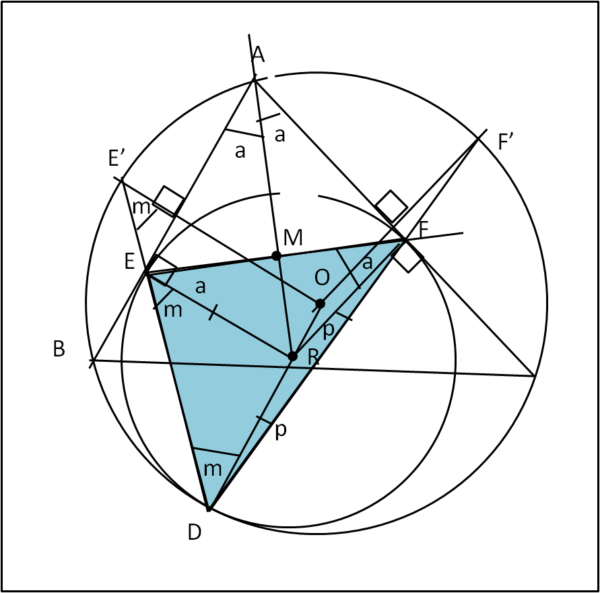
La somma degli angoli interni del triangolo EFD deve valere 180°. Scriviamolo...
m + a + a + p + p + m = 180°
Ossia:
a + m + p = 90° .... (3)
Anche questa relazione ci verrà utile tra non molto. Per adesso, riprendiamo la (2)
RD2 = AR · MR .... (2)
Questa relazione ci permette di dimostrare la similitudine di due triangoli "inaspettati", come mostra la Fig. 7
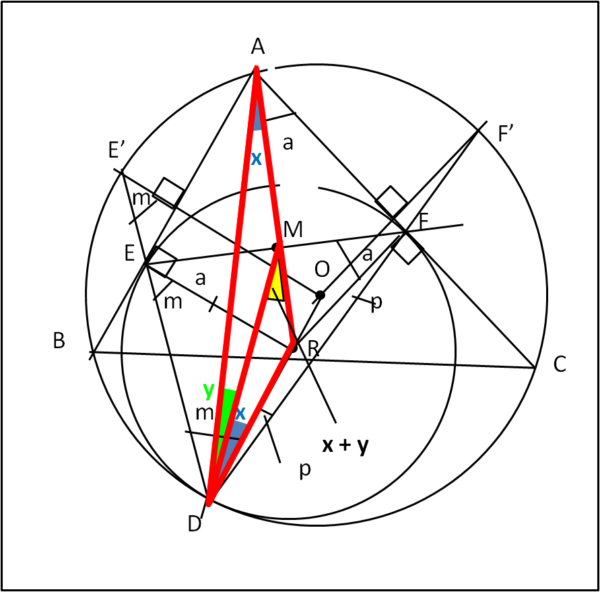
Consideriamo i triangoli ARD e MRD. La (2) ci dice che:
RD/AR = MR/RD
Inoltre l'angolo ARD è in comune.
ARD è simile a MRD
Ne segue che gli angoli blu (x) sono uguali tra loro. Chiamiamo y l’angolo verde, per cui l’angolo giallo, esterno a DAM, vale x + y:
DMR = x + y
N.B : A questo punto ricordiamo le proprietà degli angoli alla circonferenza di un certo arco TV (Fig. ![]()
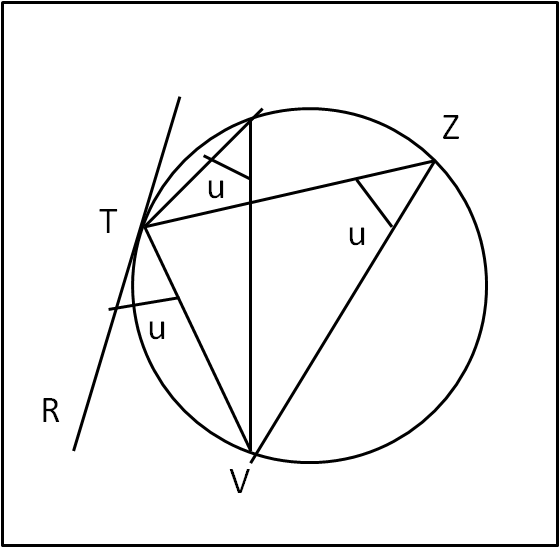
Essi sono tutti uguali tra loro e anche all'angolo limite formato dal segmento TV con la tangente alla circonferenza in T
RTV = TZV = u .... (4)
Torniamo al nostro problema e alla nuova Fig. 9
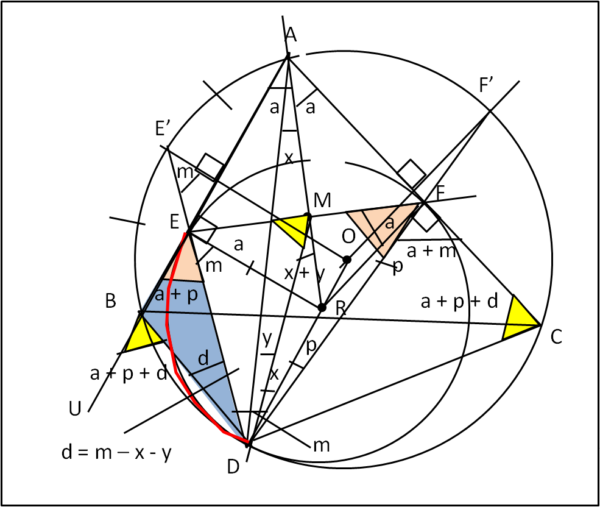
Per quanto appena ricordato (4) possiamo scrivere che l’angolo alla circonferenza EFD (rosa) è uguale all’angolo BED. Ne segue che
BED = a + p .... (5)
Consideriamo il triangolo azzurro BED e chiamiamo d l’angolo EDB. L’angolo giallo UBD è esterno al triangolo e possiamo scrivere che esso vale:
UBD = a + p + d
Notiamo che l’arco BE’ è uguale, per costruzione, all’arco E’A , dato che OA = OB e OE’ è perpendicolare ad AB.
Gli angoli alla circonferenza di due archi uguali, devono, ovviamente, essere uguali, per cui (E’ sta sulla stessa retta ED)
E’DB = E’DA = d
Abbiamo anche:
d = m – x - y
Ricordiamo che il quadrilatero ABDC è ciclico, per cui angoli opposti sono supplementari.
L’angolo ACD è supplementare ad EBD, il quale è, però, per quanto appena detto, supplementare di ACD. Ne segue che
ACD = a + p + d
Consideriamo l’angolo EMD. Esso vale:
EMD = 90 – x – y (AR è perpendicolare ad EF)
Ma sappiamo dalla (3) che
a + m + p = 90°
Per cui:
EMD = a + m + p – x – y
Ma
d = m – x – y
cioè:
EMD = a + p + d .... (6)
Torniamo all’angolo DFC
Esso vale 90 – p, ossia
DFC = a + m + p – p
DFC = a + m .... (7)
Disegniamo la Fig. 10
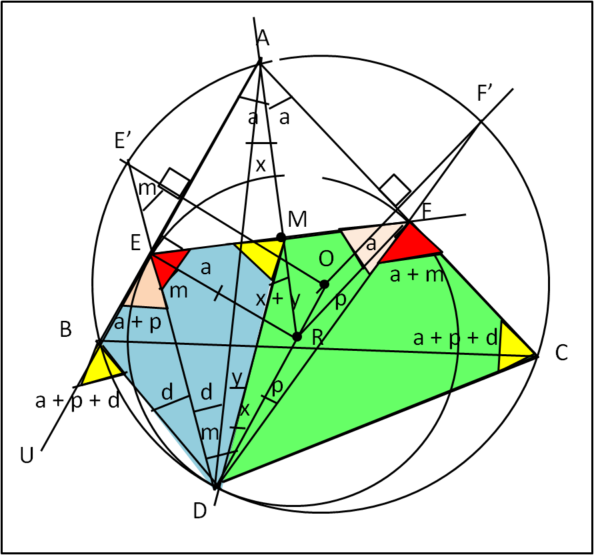
Sappiamo dalla (6) che
EMD = a + p + d
Esso è uguale all’angolo esterno UBD. Ma UBD è supplementare di EBD e quindi deve esserlo anche EMD.
EMD supplementare di EBD, ossia il quadrilatero EMDB (azzurro) è ciclico.
Così come lo è anche il quadrilatero MDCF (verde) in quanto EMD è uguale a FCD ed EMD supplementare di FMD, per cui FMD è supplementare di FCD.
Disegniamo, infine, la Fig. 11
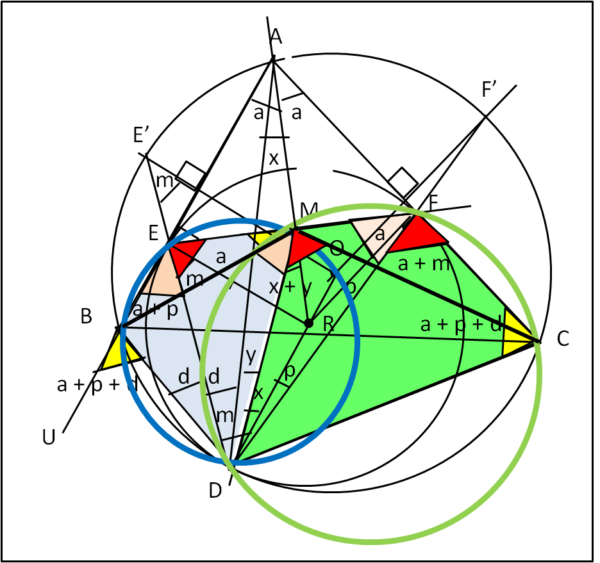
Abbiamo tracciato i due cerchi che circoscrivono i quadrilateri ciclici EBDM e MFCD.
Essendo angoli alla circonferenza possiamo scrivere:
BED = BMD = a + p (dalla (5))
DMC = DFC = a + m (dalla (7))
Ricordiamoci ciò che dobbiamo dimostrare:
BMC = 90 + a
Sommiamo BMD a DMC e otteniamo:
BMC = a + p + a + m
Non possiamo dimenticarci, però, che abbiamo dimostrato (3) che
a + p + m = 90°
Ne segue che
BMC = 90° + a
c.v.d.
E' stata dura, lo ammetto. Come già detto, potrebbero molto probabilmente esistere dimostrazioni più rapide e meno "contorte". Se qualcuno le trovasse lo indichi subito nei commenti.
Un paio di riflessioni...
Questo esercizio è stato proposto in un'olimpiade di matematica ed è stato risolto da un certo numero di ragazzi con esperienza solo liceale. In realtà la dimostrazione sfrutta teoremi elementari, ma legarli tra loro non è impresa facile, soprattutto se si ha un tempo limitato a disposizione. Io ho impiegato giorni, mentre loro solo poche ore. Tanto di cappello, perciò...
Spero, inoltre, che questo tipo di dimostrazione non solo aiuti nello sviluppare le capacità logiche e deduttive, ma serva a fare amare la geometria, una materia ricchissima di spunti e di conclusioni inaspettate.
Nel prossimo futuro scenderemo un po' di livello, sperando che qualche lettore trovi la voglia di riflettere e di risolvere i problemi proposti.
Un grazie a Maurizio, per averci provato!






14 commenti
Soluzione che non può che ispirare rispetto per l'intuito e la costanza che deve avere richiesto.
Mi tornano in mente le parole del prologo al quiz ... "dopo un po' la testa sembra andare in pallone e si scivola verso una confusione non indifferente."
Ebbene, non avendo una soluzione altrettanto generale e più lineare, propongo una breve riflessione sulle possibili soluzioni parziali, cioè valide per certi tipi particolari di triangoli.
il caso più banale è certo quello in cui il triangolo ABC è un triangolo equilatero. In questo caso, tutte le 3 costruzioni possibili sono identiche, data la simmetria. Quindi il punto M risulta inevitabilmente sempre il medesimo e dunque è l'incentro del triangolo.
Esiste però almeno un altro caso di triangolo particolare in cui si riesce facilmente a dimostrare che M è l'incentro.
Invito tutti a cercare questo triangolo e a scrivere la (semplicissima ) dimostrazione. Basta una figura con pochissime linee oltre al triangolo e al cerchio circoscritto.
Il triangolo particolare è un triangolo isoscele rettangolo, ossia questo:
L'angolo in B è un angolo retto. Il cerchio circoscritto ad ABC è facilmente costruibile considerando che l'ipotenusa AC è anche il diametro. Il centro O è il punto medio di AC.
Poniamo che il raggio del cerchio sia unitario,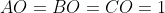 e
e 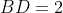
Immediato dedurre che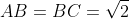
Il punto R è il centro del cerchio inscritto e tangente ai due lati AB (in E) e BC (in F) e al cerchio circoscritto (in D)
Troviamo ora la distanza RD
Ora ricaviamo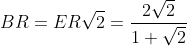
Il punto M è medio tra E ed F. Calcoliamo la distanza BM
valutiamo ora la distanza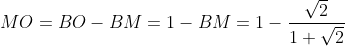
e il rapporto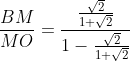
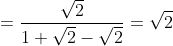
riassumendo ...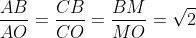
Questa catena di uguaglianze è proprio quella per cui posiamo affermare che M è l'incentro di ABC
Infatti corrisponde esattamente alla condizione trovata con il corollario al teorema della bisettirce
Quindi nel caso di questo triangolo abbiamo la prova che M è l'incentro.
Ma se il triangolo non fosse isoscele e rettangolo? come andrebbe condotta la dimostrazione?
Ebbene per un triangolo isoscele qualsiasi avremmo una situazione come quella illustrata nella figura seguente:
Ragionando sulla simmetria speculare delle due costruzioni che danno le bisettrici BM e CM possiamo affermare che il punto M è il medesimo per ambedue. Questo significa che è l'incentro.
Data l'unicità dell'incentro non è necessario dimostrare altro.
Quindi tutto il ragionamento che abbiamo esposto per il triangolo isoscele e rettangolo poteva essere scavalcato da questa semplice osservazione.
La conclusione è che la coincidenza del punto M con l'incentro è evidente e non richiede alcuna dimostrazione per tutti i triangoli isosceli.
caro Mau,
è ovvio che tutto si semplifichi grazie alla simmetria. Il problema vero è quello di ottenere il risultato per un triangolo qualsiasi che "distrugga" certe comode simmetrie.
Forse ti è sfuggito il mio primo commento, in cui scrivevo:
Ebbene, non avendo una soluzione altrettanto generale e più lineare, propongo una breve riflessione sulle possibili soluzioni parziali, cioè valide per certi tipi particolari di triangoli.
E' ovvio che sia ovvio che il problema generale da risolvere è quello di un triangolo con angoli qualsiasi.
No, non mi era sfuggito, Mau...
volevo solo far notare che il risultato per il triangolo isoscele deriva dalla simmetria e sembrerebbe che il risultato sia solo dimostrabile per questo caso particolare. Invece, questa peculiarità è dimostrabile anche per un triangolo privo di simmetrie. Ne deriva che il fatto di avere una simmetria non è condizione necessaria. Era solo una riflessione ...
Ok , ok ... assolutamente d'accordo.
Salve.
Ho provato a cimentarmi con il problema diabolico.
Sono arrivato ad un risultato che mi sembra convincente.
Ma per sottoporre l'idea alla vostra valutazione ho bisogno di allegare dei disegni.
Se qualcuno mi indica come fare e dove trovare le istruzioni utili allo scopo, posto le mie elucubrazioni.
Caro sprmnt21,
per prima cosa devi caricare l’immagine su un sito apposito (per esempio https://imgur.com ma ce ne sono sicuramente altri), dopodiché copi l’indirizzo url dell’immagine che ti fornisce quel sito, clicchi sull’icona “inserisci/modifica immagine” (quella col simbolo stilizzato di montagna e sole), incolli l’url nel campo sorgente (se non vedi comparire niente è perché i caratteri sono bianchi) quindi clicchi su ok.
Spero di averti dato istruzioni comprensibili, in caso contrario scrivimi a infinitoteatrocosmo@gmail.com
Vediamo se funziona.
Facciamo una prova.
Io non vedo la immagine collegata.
ho messo questo link nel campo della sorgente del pannello inserisci/modifica immagine e dato l'OK
https://imgur.com/a/HsBjLeS
Ho provato anch’io ad inserire l’immagine con quel link ed effettivamente non funziona, immagino che dipenda da qualche impostazione sulla condivisione impostata su imgur, ma non saprei come verificare.
Comunque sia, la buona notizia è che cliccando sul link l’immagine si vede, quindi puoi inserire il link nel tuo commento e chi è interessato può aprirlo
Per quanto riguarda la costruzione del triangolo interno si può utilizzare la proprietà asserita dall'esercizio.
Quindi si traccia una ortogonale alla bisettrice in A passante per l'incentro di ABC. Questa interseca i lati nei punti di tangenza. Quindi da uno di questi la perpendicolare al lato interseca la bisettrice nel centro del cerchio interno.
Oppure si può seguire il procedimento più generale illustrato nella figura seguente