(Q) Due rettangoli a confronto (con soluzione)***
La soluzione è stata data in modo più che esauriente nei commenti di Andy...
Ecco, perciò, un quiz puramente geometrico da risolvere senza fare uso della trigonometria. La parte più "difficile" è -forse- la costruzione dei due rettangoli. Poi, ci vuole solo un po' di ragionamento e di fantasia...
(1) Costruzione del rettangolo rosso (Fig. 1)
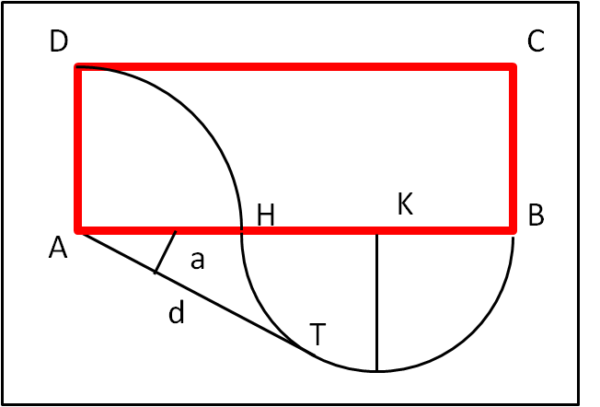
Il rettangolo rosso ABCD è costruito in modo che AH = DA = raggio di un quarto di cerchio, mentre HB sia il diametro di un semicerchio di centro K. Ciò che conosciamo è la lunghezza del segmento AT = d, tracciato da A e tangente al semicerchio.
(2) Costruzione del rettangolo azzurro (Fig. 2)
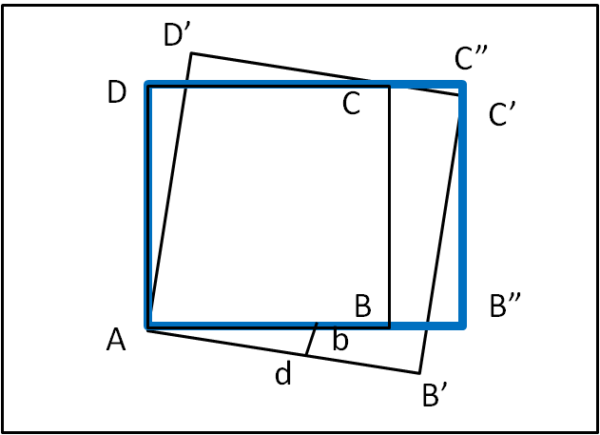
Il rettangolo azzurro AB”C”D è formato da un quadrato (ABCD) e da un rettangolo (CC”B”B) in modo tale che esista un quadrato AD’C’B’ tale che l’intersezione di DC’ con DC” coincida con C e il vertice C’ sia sul lato C”B” del rettangolo.
Si chiede:
Nell'ipotesi che AT = AB' = d sia l'unico dato conosciuto del problema
(I) Calcolare le due aree e dire (II) che relazione esiste tra a e b affinché le due aree risultino uguali.
Il problema non è realmente complicato, ma permette di fare qualche ulteriore ragionamento sulla costruzione dei due rettangoli.






4 commenti
Qui il mio ragionamento circa il calcolo delle aree:
https://i.ibb.co/H7zRYZb/2-rettangoli-1.png
Caro Enzo,
intendi per a e b gli angoli, rispettivamente, TAB vertice A di figura 1 e B'AB'' vertice A di figura 2?
esattamente, caro Andy ...
Per come sono costruiti i due rettangoli, l’area di entrambi sembra essere funzione solamente della dimensione del segmento d.=AH^2&space;+&space;2AH&space;\times&space;HK&space;=&space;d^2) .
.

&space;\times&space;d&space;\sqrt2=d^2) ;
;
Per la figura 1, ferma restando la dimensione d, se faccio diminuire l’ampiezza dell'angolo a facendolo tendere a zero, il raggio AD=AH del quarto di circonferenza tende verso d mentre il raggio KH=KB della semicirconferenza tende a zero; in poche parole AD→d e AB→d ovvero il rettangolo ABCD tende al quadrato di lato d.
Se invece faccio aumentare l’ampiezza dell’angolo a, AD tende a diminuire mentre HB tende ad aumentare, “stirando” il rettangolo ABCD secondo il lato AB, ma la su area rimane sempre
Per la figura 2, sempre ferma restando la dimensione del segmento d, diminuendo l’angolo b facendolo tendere a zero, CC’’ tende a zero, AD=AB tende alla lunghezza d, per cui il rettangolo tende al quadrato ABCD di aerea
Se invece si fa aumentare l’angolo b, CC’’ aumenta e il rettangolo si stira secondo il lato AB’’. Ad esempio per b=45°, AB’’ diventa uguale alla diagonale del quadrato di lato d, cioè d√2, AD diventa metà della stessa diagonale ovvero d√2 / 2, l’area del rettangolo AB’’C’’D sarà:
quindi, indipendentemente da una relazione tra gli angoli a e b, l’area dei rettangoli sarà uguale solo in funzione della lunghezza data d.
sempre preciso ed esauriente...