L'ideale nel calcolo di un integrale doppio sarebbe avere un rettangolo come dominio di integrazione in un certo piano. Normalmente non è così, per cui sarebbe bello riuscire a ottenerlo attraverso un cambiamento di coordinate.

Cambiamento di coordinate

Facciamo subito un esempio che tratteremo nuovamente alla fine della determinazione del determinante jacobiano, la cui importanza verrà spiegata nel modo più semplice possibile.

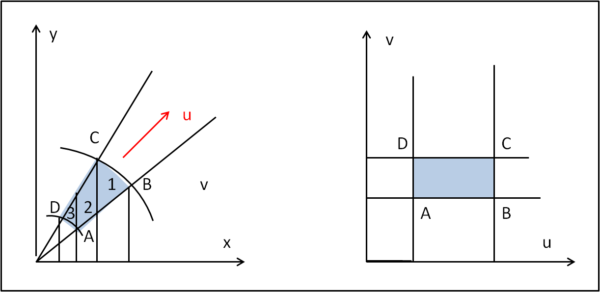
Immaginiamo, perciò, di volere calcolare l'integrale doppio di una certa funzione φ(x,y) nel dominio descritto nella Fig. 1, a sinistra.

 

∫∫_dA f(x,y) dx dy

La faccenda non è certo semplice dato che il dominio di partenza deve essere diviso in più parti (1,2 e 3) poiché cambiano le funzioni y = φ(x) che lo delimitano. Se volessimo ridurre il tutto a integrali semplici dovremmo, inoltre, calcolare le tre parti attraverso una differenza di integrali. Si può certamente fare e spesso risulta essere il metodo più rapido, ma a noi interessa trattare il caso più generale possibile che, spesso, per funzioni complicate, diventa l'unico possibile.

La Fig. 1, a destra, ci mostra un banale cambiamento di variabili. Al posto di x e y  consideriamo il nuovo sistema definito dal raggio r e dall'angolo t che esso descrive. Eseguito questo cambiamento, ecco che quasi miracolosamente lo strano dominio di sinistra diventa il rettangolo di destra, che ha dei limiti ben definiti e numerici. x e y diventano funzioni di u e v, capaci di costruire il rettangolo. In questo caso basta utilizzare:

x = x(u,v) = x(r,t) = r cos t

y = y(u,v) = y(r,t) = r sin t

La Fig. di destra ci farebbe pensare che la faccenda possa risolversi immediatamente, inserendo x(u,v) e y(x,y) al posti di x e y

∫∫_dA f((r cost), (r sin t)) dx dy

Ovviamente deve cambiare anche il dominio, ossia il dA deve diventare una certa area dB. Niente di più facile come mostra la Fig. 1b:

dB = dr dt

Infine devono cambiare anche i differenziali dx e dy. Potremmo pensare di scriverli brutalmente  come dr dt. Bene, facessimo così, il nuovo integrale NON sarebbe assolutamente uguale a quello di partenza. Potete anche provare a svolgere i calcoli e vi accorgerete che è la "dura" e pura verità.

In realtà, il fatto che quanto fatto sia sbagliato si può intuire poiché, facendo così, la nuova area dB = dr dt  risulterebbe uguale a dx dy. E questo non è vero!

Avrete già capito che la trasformazione di coordinate è sicuramente un metodo che semplifica i calcoli, ma deve introdurre una specie di fattore di scala  J capace di deformare l'area di partenza.

Tutto sta, quindi, nella determinazione del fattore di scala che deve essere una funzione di r e t o, più in generale, di u e v.

In termini puramente matematici:

dx dy = |J| (u,v) du dv

Il fattore di scala o Jacobiano

Vediamo di capire bene cos'è J e come si può calcolare nel caso più generale possibile. Torniamo quindi a un cambio di variabili del tipo generico:

x = x(u,v)

y = y(u,v)

Prima, ho imposto che venga considerato un valore sempre positivo di J, utilizzando, perciò, il suo valore assoluto, dato che stiamo parlando di lunghezze quindi di valori positivi. J può essere sia minore che maggiore di 1, ossia può schiacciare o allargare l'area, ma non può certo darne un valore negativo.

Ciò che vogliamo fare è dimostrare che esiste l'uguaglianza tra due integrali doppi se scrivo:

I = ∫∫_D f(x,y) dx dy = ∫∫_E f(x(u,v),y(u,v)) |J| du dv

In altre parole, l'uguaglianza è verificata se:

dx dy = |J (u,v)| du dv

Ribadisco che il tutto si restringe al calcolo di due aree di cui una è la trasformata dell'altra. Questa scrittura ci dice che non basta cambiare i lati dx e dy e nemmeno moltiplicarli per un certo fattore costante, ma è necessario che questo fattore (proprio J) sia anch'esso una funzione di u e v.

Disegniamo la Fig. 2 e consideriamo la sua parte in alto, con il dominio complicato D.

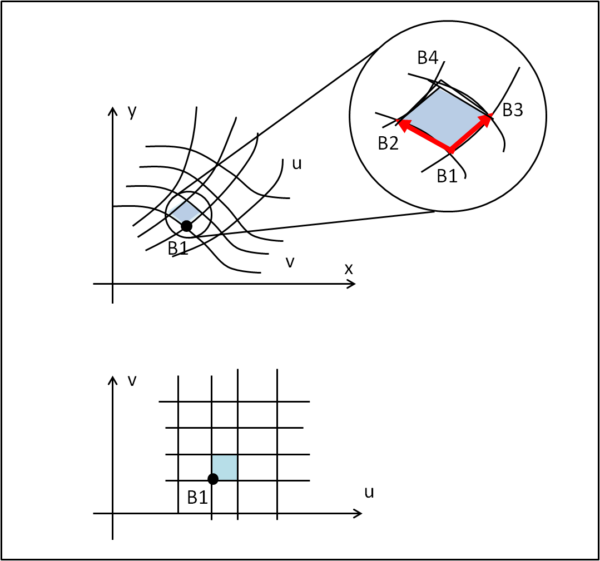
Questo dominio deve portarci al dominio "rettangolare" E.  Cosa significa questa frase, in generale? Solo e soltanto che nella Fig. 2 (in alto) il dominio è caratterizzato da tante aree infinitesime legate alle nuove coordinate u e v, le stesse che ci permetterebbero di ottenere un dominio E in cui le aree infinitesime diventerebbero dei piccoli rettangoli, con i lati paralleli ad ascisse e ordinate.

Prendiamo un punto qualsiasi B1 (x(u,v), y(u,v)), e costruiamo un'area infinitesima aggiungendo du e dv alle coordinate di B1 e assumendo che i tratti di curva che delimitano quest'area siano rettilinei. Possiamo farlo, dato che i tratti sono infinitesimi. Otteniamo un parallelogramma e non un rettangolo, dato che u e v seguono curve non perpendicolari tra loro. I suoi lati infinitesimi sono du e dv.

Tuttavia, abbiamo imparato a calcolare l'area di un parallelogramma, facendo il prodotto vettoriale di due vettori. Nel nostro caso i vettori sono B1B2 e B1B3 (poco ci importa del punto B4). Quali sono le coordinate di questi punti e le componenti dei due vettori? Facile a scriversi:

B1  =  (x(u, v), y(u, v))

B2  = (x(u + du, v), y(u + du, v))

B3 = (x(u, v + dv), y(u, v + dv))

B1B2  = (x(u + du, v) - x(u, v), y(u + du, v) - y(u, v))

B1B3 = (x(u , v + dv) - x(u, v), y(u, v + dv) - y(u, v))

Cosa abbiamo scritto ? Qualcosa di piuttosto semplice. Ad esempio, prendiamo  la prima componente di B1B2

x(u + du,v) - x(u,v)

moltiplichiamola e dividiamola per du.

((x(u + du,v) - x(u,v))/du) du

Vi ricorda qualcosa la parte in neretto? Dovrebbe e come!

Cosa rappresenta la scrittura:

(f(x + h) - f(x))/h

Solo e soltanto il rapporto incrementale il cui limite per h che tende a zero risulta essere proprio la derivata di f(x)

Al posto di una funzione a una sola variabile, utilizziamo una funzione a due variabili f(x,y)

Bene la parte in neretto di prima è proprio il rapporto incrementale della funzione, quando di consideri y  costante, ossia quello che ci permette di calcolare, passando al limite, la derivata parziale di f(x,y) rispetto a x. Assumendo il rapporto incrementale come la derivata stessa, nel nostro caso (possiamo prendere du piccolo a piacere), abbiamo quindi che:

(x(u + du,v) - x(u,v))/du = ∂x(u,v)/∂u

Per avere la prima componente di B1B2 basta moltiplicare la derivata parziale per du:

(∂x(u,v)/∂u) du

In modo analogo, la seconda componente di B1B2 è data da:

(∂y(u,v)/∂u) du

la prima di B1B3 è

(∂x(u,v)/∂v) dv

mentre la seconda è:

(∂y(u,v)/∂v) dv

Per calcolare l'area del parallelogramma B1B2B3B4 basta calcolare il determinante che contiene le coordinate dei due vettori. Eseguendo le moltiplicazioni incrociate ci accorgiamo che entrambi i membri contengono du · dv, per cui possiamo portare fuori dal determinante il prodotto du · dv. Ne segue che l'area è data da:

Il determinante viene chiamato Jacobiano ed è proprio il fattore che trasforma le aree come desiderato.

Effettuando questa moltiplicazione riusciamo a far diventare rettangolini i parallelogrammi del dominio D, ossia riusciamo a trattare la parte alta della Fig. 2  in termini della parte bassa. Ovviamente, va scelta la giusta trasformazione.

Non spaventatevi dalla formula... Normalmente lo Jacobiano è uguale a qualcosa di veramente semplice ed è, soprattutto, sempre lo stesso per ogni trasformazione, ossia la scelta di un certo cambiamento di variabili dà sempre luogo allo stesso Jacobiano.

Il prodotto |J| du dv è quindi l'area che deve prendere il posto di dx dy. Nel caso della classica trasformazione in coordinate polari, abbiamo:

x = x(u, v) = r cos t

y = y(u, v) = r sin t

∂x/∂r = cos t

∂y/∂r = sin t

∂x/∂t = - r sin t

∂y/∂t = r cos t

|J| = |(∂x/∂r)(∂y/∂t) - (∂y/∂r)(∂x/∂t)

|J| = r cos2 t - (- r sin2 t) = r (cos2 t + sin2 t)

|J|= r

L'integrale di partenza, ossia

∫∫_dA f(x,y) dx dy

va quindi trasformato in

∫∫_dB f((r cost),(r sint))  r dr dt              .... (1)

Ovviamente, ponendo f uguale a una costante h otterremmo il volume di un cilindroide, ponendolo proprio uguale ad 1 otterremmo l'area della base del cilindroide ossia quella del dominio D. Ribadiamo ancora che la trasformazione utilizzata trasforma il cilindroide in un parallelepipedo e il dominio D in un rettangolo.

Proviamo subito a dimostrare che tutto funziona perfettamente. Poniamo proprio φ = costante = 1, in modo da limitarci all'area del dominio. Possiamo considerare come dominio un cerchio di raggio r centrato nell'origine.  Eseguiamo la trasformazione utilizzando la formula (1):

∫∫_dB r dr dt  = ∫₀^2π dt ∫₀^r r dr = ∫₀^2π dt [r²/2]₀^r= ∫₀^2π r²/2 dt = r²/2 [t]₀^2π = 2πr²/2 = πr²

Riassumiamo ancora cosa abbiamo fatto: dovendo calcolare un integrale doppio in un dominio non semplice abbiamo cambiato le coordinate in modo che il dominio diventasse un rettangolo. Per far ciò è stato necessario trovare l'area infinitesima del primo dominio che si trasformasse in un'area infinitesima rettangolare nel secondo dominio.

Fermiamoci qui, ma la prossima volta faremo qualche esempio pratico che forse ci aiuterà a capire  ancora meglio la procedura da seguire.

continua ...