In questo e nei futuri articoli faremo qualche esempio in cui è molto utile un cambiamento di coordinate. Questa volta sfioreremo appena lo Jacobiano per dare maggiore importanza alla trasformazione del dominio e al calcolo dell'integrale. Ricordiamoci, però, che senza di lui il risultato sarebbe sbagliato!

A tal proposito ricordiamo che all'interno dell'integrale compare anche la funzione φ(x,y) e questo può rendere molto complicato se non addirittura impossibile il calcolo attraverso le coordinate x e y. In altre parole, non dobbiamo guardare solo il dominio nel piano x,y, ma anche la possibilità di integrare in un dominio apparentemente semplice una certa funzione φ. Proprio  questa funzione può darci lo spunto per effettuare il più idoneo cambiamento di coordinate.

Un caso molto semplice

Vogliamo calcolare l'integrale doppio della funzione φ(x, y ) = (x + y)² in un certo dominio A del piano x,y

∫∫_A (x + y)² dx dy

nel dominio definito da:

1 ≤ (x² + y²) ≤ 4

0 ≤ x ≤ y ≤ √3 x                           .... (1)

N.B: dedicata ad Albertone (e a chi lo segue in incognito...)

Con le nozioni imparate finora potete risolvere l'integrale da soli. Perché non provarci, prima di continuare nella lettura dell'articolo?

Notiamo subito che

x² + y² = r²

è l'equazione della circonferenza di raggio r. Ne segue che la prima relazione dice praticamente che sono ammesse nel dominio tutte le circonferenze con raggio compreso tra 1 e 2.

Passiamo alla seconda relazione.

Essa ci dice che x ≥ 0, ossia ci dice che dobbiamo limitarci al primo e al quarto quadrante. Non solo, però, essa dice che anche y ≥ 0. Ne segue che viene eliminato anche il quarto quadrante. Il dominio deve essere, perciò, nel primo quadrante e compreso da due quarti di circonferenza. Non è finita... la relazione dice anche che la retta y = x è un limite ulteriore e, in particolare è ammessa la parte in cui y ≥ x, ossia la parte del primo quadrante che sta sopra la retta. Infatti solo quei punti hanno la loro x è minore della loro y. Infine, ci dice anche che la retta y = √3x e un altro limite e sono ammessi questa volta solo i punti che stanno al di sotto di tale retta, ossia quelli per cui y ≤ √3x. In conclusione, la Fig. 1 descrive geometricamente il dominio di integrazione.

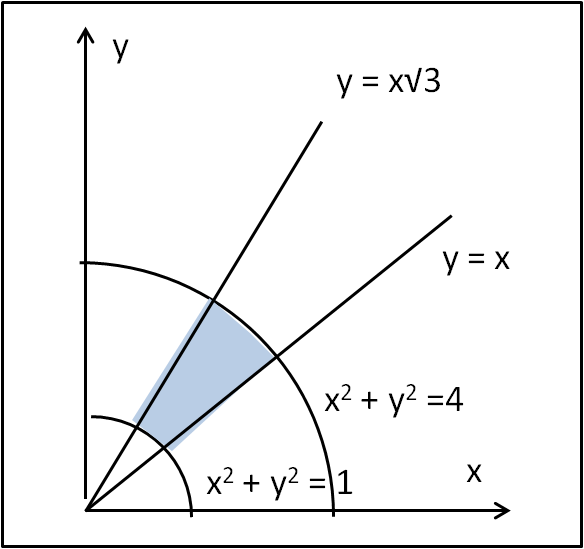
N.B.: Fate sempre molta attenzione alla descrizione geometrica del dominio, dato che è fondamentale conoscere i suoi estremi per poter passare al calcolo di integrali definiti. Controllate, perciò, sempre, che i punti del dominio da voi costruito soddisfino tutte le condizioni date dalle (1).

Come al solito, si potrebbe pensare di passare al calcolo dell'integrale della funzione φ(x,y), che è poi il cilindroide che ha per base il dominio appena costruito e come altezza proprio φ(x,y). Si potrebbe certamente, ma questa volta ha fatto la sua comparsa una φ che non è costante, ma variabile da punto a punto del dominio.

Conviene affidarsi a un cambiamento di variabili e,  avendo a che fare con limiti di dominio che sono parti di circonferenza, si dovrebbe immediatamente pensare alle coordinate polari r e t, ossia a quelle che sono legate a x e y dalle "celebri" relazioni:

x = r cos t

y = r sin t

dove r è proprio il raggio e t è l'angolo da lui decritto nel dominio.

Andiamo a vedere come si trasforma il dominio A.

La variabile r è compresa tra 1 e 2, mentre la variabile t non è altri che l'angolo che ha per tangente il coefficiente angolare delle rette y = x e y = √3x. La prima retta ha coefficiente angolare uguale a 1 e, quindi, l'angolo t corrispondente e quello la cui tangente è 1, ossia π/4 (45°). La seconda, invece, ha coefficiente angolare √3 e quindi l'angolo t risulta π/3 (60°).

Notiamo che il cambiamento di variabili ha trasformato un dominio delimitato da funzioni y = f(x), più meno semplici, in un dominio delimitato da costanti, ossia in un rettangolo, proprio quello che si vorrebbe sempre ottenere.

Siamo pronti a calcolare il nostro integrale doppio, inserendo r e t al posto di x e y, senza dimenticarci, però, di moltiplicare dr dt per lo Jacobiano relativo alle coordinate polari che, come visto nell'articolo precedente, non è altri che r.

∫∫_A (x + y)² dx dy = ∫∫_B (x(r,t) + y(r,t))² r dr dt = ∫∫_B (r cost + r sin t)² r dr dt

Abbiamo, ovviamente, cambiato il dominio A nel dominio "rettangolare" B

Esprimiamo meglio l'integrale doppio:

∫_π/4^π/3 dt ∫₁²(r cost + r sin t)² r dr = ∫_π/4^π/3 dt ∫₁²r²(cost + sin t)² r dr =

= ∫_π/4^π/3 (cost + sin t)²dt ∫₁²r³ d r

Avete notato che ho portato fuori dall'integrale più interno tutto ciò che non dipende da r

Eseguiamo il quadrato di cos t + sin t

∫_π/4^π/3 (cost + sin t)²dt ∫₁²r³d r  = ∫_π/4^π/3 (cos²t + sin² t + 2 sin t cos t)dt ∫₁²r³d r =

= ∫_π/4^π/3 (1 + 2 sin t cos t)dt ∫₁²r³d r = ∫_π/4^π/3 (1 + sin (2t))dt ∫₁²r³d r

Abbiamo utilizzato la formula di duplicazione del seno, già trattata in altri articoli trigonometrici, ossia:

2 sint  cos t = sin (2t)

Iniziamo al calcolare l'integrale più interno. Sappiamo bene che l'integrale di r³ vale r⁴/4, per cui:

∫_π/4^π/3 (1 + sin (2t))dt 1/4 [r⁴]₁²  = 15/4∫_π/4^π/3 (1 + sin (2t))dt

L'ultimo integrale rimasto vale t - cos (2t)/2 (la funzione la cui derivata è sin 2t è infatti - cos(2t)/2)

15/4 [t - cos (2t)/2]_π/4^π/3dt  = 15/4 ((π/3 - cos (2π/3)/2) - (π/4 - cos (π/2)/2)) = 15/4(π/3 - 1/4 - π/4)

= (15/4) (- 1/4 + π/12)

E, infine:

∫∫_A (x + y)² dx dy = 5/16(π - 3)

Ho voluto fare tutti i passaggi, anche i più banali, sperando di essere il più didattico possibile.

Un integrale più difficile

Facciamo un altro esempio di cambiamento di coordinate in cui la funzione φ(x,y) sia proprio l'ideale per questa operazione.

L'integrale sia:

∫∫_A arctan(y/x) dx dy

e il dominio sia lo stesso di quello dell'esercizio precedente. ossia compreso tra due archi di circonferenza di raggi 1 e 2 e tra le due rette y=x e y =√3 x. Non abbiamo, perciò, bisogno di una nuova figura.

Senza cambiamento di coordinate l'integrale di un arcotangente calcolato su "pezzi" di dominio non sarebbe cosa facile.

Molto più rapida è la soluzione effettuando il "solito" cambio di coordinate da cartesiane a polari.

x = r cos t

y = r sin t

Non solo trasformiamo il dominio in un rettangolo, ma scriviamo la funzione φ(x,y) in modo veramente banale:

φ(x,y) = arctan y/x = arctan (r sin t/(r cos t)) = arctan (tan t) = t

La funzione è diventata soltanto t:

∫∫_A arctan(y/x) dx dy = ∫∫_B t r dr dt = ∫₁² r dr∫_π/4^π/3 t  dt

∫₁² r dr∫_π/4^π/3 t  dt = ∫₁² r dr[t²/2]_π/4^π/3 = 1/2∫₁² (π²/9 - π²/16) r dr = (1/2)π²(7/144)∫₁² r dr =

= (1/2)π²(7/144) (1/2) [r²]₁² = (1/2)π²(7/144) (1/2)3 = π²(7 3)/(4 144) = 7π²/192

∫∫_A arctan(y/x) dx dy = 7π²/192

La prossima volta continueremo con altri esempi, per funzioni decisamente più interessanti e anche per Jacobiani diversi...

continua ...

P.S.: sicuramente mi è sfuggito qualche errore di sbaglio, ma ci pensa Albertone... ;-)