Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

 

Il problema di base sembrerebbe piuttosto semplice, dato che nasce dal classico e generale problema “dei tre corpi”. Esso chiede soltanto, date due masse orbitanti attorno al comune baricentro, di descrivere il moto di un terzo oggetto che si trovi immerso nel campo gravitazionale degli altri due.

Bene, questo è un problema che è analiticamente irrisolvibile e si riesce a descrivere solo attraverso iterazioni successive e semplificazioni varie. In poche parole, il terzo corpo dovrebbe anch’egli rivolvere attorno al baricentro del sistema, ma nel far ciò è disturbato dalle forze di gravitazione delle due masse principali che variano da punto a punto.

Il modo più semplice per trattare il problema è quello di considerare la massa del terzo corpo del tutto trascurabile rispetto alle altre due. Anche così, però, le cose non sono certamente semplici. Esistono, tuttavia, cinque punti estremamente particolari: essi rimangano FERMI rispetto al sistema in rotazione. In altre parole, se ci poniamo nel sistema che ruota, vedremo questi punti sempre nella stessa posizione rispetto alle due masse che “costruiscono” il campo gravitazionale. Succede, praticamente, quello che ci mostra l’animazione di Fig. 1.

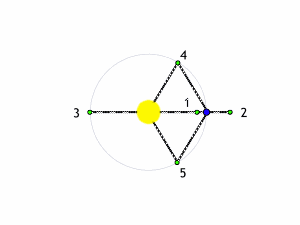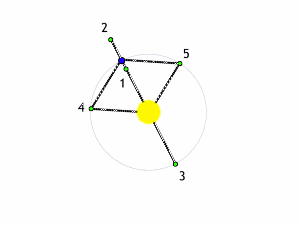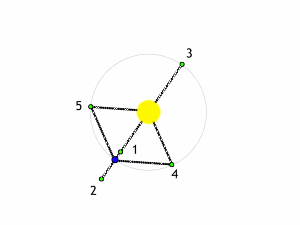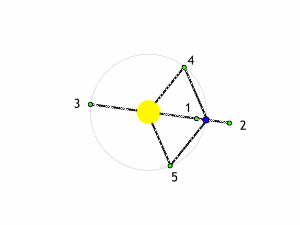
E’ facile capire come questi punti, di origine puramente teorica, abbiano ripercussioni pratiche enormi, dato che se al posto delle due masse consideriamo la Terra e il Sole, ad esempio, essi rappresentano posizioni ideali per osservare diversi oggetti celesti, dato che caso per caso non vengono disturbati dal moto relativo della Terra e del Sole. Tutto è infatti immobile, in perfetto equilibrio.

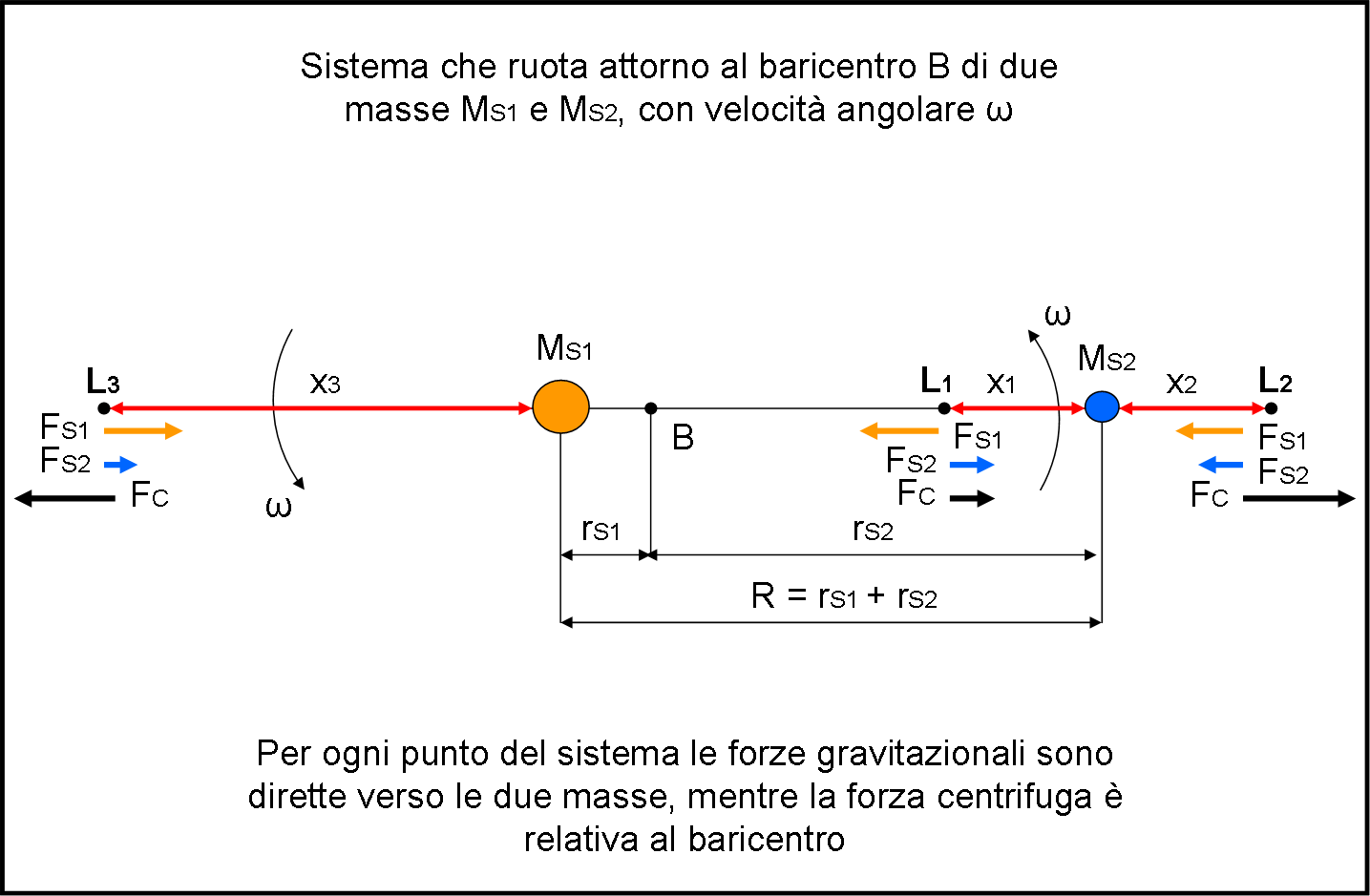
Prima di iniziare, diciamo subito che dei cinque punti, due (L₄ e L₅) sono posti ben al di fuori della congiungente Terra-Sole. Li conosciamo già molto bene e li tratteremo a parte. Occupiamoci, per adesso, di L₁, L₂ e L₃ che si trovano tutti allineati tra loro. Disegniamo la Fig. 2 che illustra perfettamente il problema, le distanze e le forze in gioco.

M_S1 e M_S2 sono le masse dei due corpi principali che ruotano attorno al comune baricentro B  con velocità angolare ω. L₁, L₂ e L₃ sono i tre punti lagrangiani, dove, come già detto, le forze gravitazionali delle due masse principali vengono controbilanciate dalla forza centrifuga. Vediamo cosa succede, caso per caso.

Un oggetto posto in L₁ orbita in una posizione più vicina a M_S1  di quella di M_S2 . Dovrebbe, perciò, avere un periodo di rivoluzione più corto (terza legge di Keplero). Tuttavia, non si può ignorare l’effetto gravitazionale dovuto a M_S1 . Se l’oggetto si trova nella direzione M_S1 -M_S2 , la forza di  M_S2 controbilancia in qualche modo la forza gravitazionale del corpo di massa M_S1  e allunga il periodo orbitale dell’oggetto. Più si avvicina a M_S2  e più l’effetto cresce. Nel punto L₁ il periodo orbitale diventa esattamente uguale a quello dell’oggetto di massa M_S2 , anche se le loro posizioni non coincidono.

Dalla parte opposta della massa M_S2 , il periodo orbitale è invece più lungo di quello di M_S2 . Tuttavia, la forza gravitazionale di M_S2  si somma a quella di M_S1 , accorciando il periodo orbitale fino a che, in L₂, esso uguaglia nuovamente quello di M_S2 .

L₃, invece, si trova dalla parte opposta di M_S1 , su un’orbita appena più larga di quella di M_S1 , ma più vicina a M_S1  di quanto non sia M_S2 . Quanto detto non è un’assurdità, dato che le orbite si compiono attorno al baricentro di M_S1  e M_S2 . La somma delle forze gravitazionali di M_S1  e M_S2  porta l’oggetto in L₃ a ruotare con lo stesso periodo di M_S2 .

Normalmente, M_S2 è decisamente minore di M_S1 (Terra-Sole, Luna-Terra)

Come si intuisce molto bene, per descrivere i tre punti è necessario fare agire tre forze: quelle gravitazionali di M_S1  e M_S2  e quella centrifuga che deve controbilanciarle. In particolare: In L₁ abbiamo un forza F_S1 maggiore di quella F_S2 e di verso opposto. La risultante deve essere uguale e contraria alla forza centrifuga F_C agente in quel punto. In L₂ e L₃ le due forze gravitazionali si sommano e la somma deve essere uguale e contraria alla forza centrifuga.

Non ci resta, quindi, che scrivere per esteso queste tre relazioni, chiamando x₁, x₂ e x₃ le distanze dei punti lagrangiani dalla massa M_S2 (i primi due) e da M_S1 (il terzo). R è la distanza tra le due masse e r_S1 e r_S2 sono le distanze delle due masse dal comune baricentro. Ovviamente, poniamo tutte le orbite circolari, altrimenti le cose si complicherebbero enormemente, dato che varierebbero costantemente le distanze relative e quindi anche le posizioni dei punti lagrangiani. Fidatevi di me: basta e avanza!

Le tre equazioni sono :

L₁

F_S1 = F_S2 + F_C       …. (1)

L₂

F_S1 + F_S2 = F_C       …. (2)

L₃

F_S1 + F_S2 = F_C       …. (3)

Veramente banali… a prima vista.

Per esprimere la forza centrifuga agente su una massa m, basta ricordare che:

F_C = mrω²

Nel caso della massa M_S2, ad esempio, questa forza deve bilanciare esattamente la forza gravitazionale di M_S1 agente su M_S2. Ricordiamo che la forza di gravità dipende dalla distanza tra le due masse, mentre la forza centrifuga è riferita al baricentro del sistema. Si ha, quindi:

F_C = M_S2r_S2 ω² = GM_S1M_S2/R²

Da cui

ω² = GM_S1/r_S2R²    …. (4)

Però, si può anche scrivere:

F_C = M_S1r_S1ω² = GM_S1M_S2/R²

Da cui

ω² = GM_S2/r_S1R²    …. (5)

In poche parole, possiamo esprimere la velocità angolare in funzione delle masse M_S1 e M_S2 e della distanza tra le due masse dal baricentro. Tenendo conto che la velocità angolare deve essere la stessa anche per l’oggetto di massa m posto in L₁, L₂ e L₃, abbiamo che la forza centrifuga per i tre punti diventa:

L₁

Usando la (4)

F_C = m(r_S2 - x₁)ω² = GmM_S1(r_S2 – x₁)/r_S2R²

L₂

Usando la (4)

F_C = m(r_S2 + x₂)ω² = GmM_S1(r_S2 + x₂)/r_S2R²

L₃

Usando la (5)

F_C = m(r_S1 + x₃)ω² = GmM_S2(r_S1 + x₃)/r_S1R²

Tutto bene fin qui? Direi di sì… abbiamo solo sostituito una velocità angolare costante all’interno delle forze centrifughe corrispondenti ai singoli punti di equilibrio.

Passiamo ora a scrivere le forze gravitazionali delle due masse M_S1 e M_S2 agenti sui tre punti lagrangiani:

L₁

F_S1 = GmM_S1/(R - x₁)²

F_S2 = GmM_S2/x₁²

L₂

F_S1 = GmM_S1/(R + x₂)²

F_S2 = GmM_S2/x₂²

L₃

F_S1 = GmM_S1/x₃²

F_S2 = GmM_S2/(R + x₃)²

Utilizzando la Fig. 2 è proprio un gioco da bambini!

Siamo pronti, adesso, a scrivere per esteso le equazioni (1), (2) e (3)

F_S1 = F_S2 + F_C

GmM_S1/(R - x₁)² = GmM_S2/x₁² + GmM_S1(r_S2 – x₁)/r_S2R²            …. (1)

F_S1 + F_S2 = F_C

GmM_S1/(R + x₂)² + GmM_S2/x₂² = Gm M_S1 (r_S2 + x₂) /r_S2R²        …. (2)

F_S1 + F_S2 = F_C

GmM_S1/x₃² + GmM_S2/(R + x₃)² = Gm M_S2 (r_S1 + x₃) /r_S1R²        …. (3)

Che si semplificano dato che Gm appare in tutti i termini

M_S1/(R - x₁)² = M_S2/x₁² + M_S1(r_S2 – x₁)/r_S2R²          …. (1)

M_S1/(R + x₂)² + M_S2/x₂² = M_S1 (r_S2 + x₂) /r_S2R²         …. (2)

M_S1/x₃² + M_S2/(R + x₃)² = M_S2 (r_S1 + x₃) /r_S1R²       …. (3)

Perfetto! Veramente semplice

Abbiamo tre equazioni in cui l’unica incognita è, per ognuna di esse, x₁, x₂ e x₃, rispettivamente. Infatti, le masse dei due corpi principali sono note, così come la loro distanza e quella dal baricentro. Non ci resta che risolvere, una per una, le equazioni e trovare, rispettivamente, x₁, x₂ e x₃.

Provate, provate pure… ma vi consiglio di desistere subito…

Ognuna di loro è un’equazione di quinto grado! Non ci credete? Provate a ridurle allo stesso denominatore. Nel primo caso esso diventa: (R - x₁)² x₁² r_S2R². Il numeratore del terzo termine deve, perciò, essere moltiplicato per (R - x₁)² x₁² e, quindi, diventa M_S1(r_S2 – x₁) (R - x₁)² x₁². Come volevasi dimostrare: la x₁ compare alla quinta potenza!

La soluzione dell’equazione diventa un’operazione non certo banale e si ottiene attraverso vari “trucchi” sia grafici che di interazioni successive. Delle cinque soluzioni, bisogna scegliere quella “buona”, ossia per L₁, ad esempio, quella che cade tra 0 e 1. in termini di distanza tra M_S1 e M_S2.

A titolo di esempio riportiamo i valori dei tre punti lagrangiani nei sistemi Sole-Terra e Terra-Luna.

Sole-Terra (R = 149.600.000 km)

x₁ = 1.501.557 km

x₂ = 1.491.557 km

x₃ = 149.599.737 km

Terra-Luna (R = 384.401 km)

x₁ = 64.499 km

x₂ = 58.006 km

x₃ = 381.678 km

I valori riportati sono valori medi, dato che le orbite sono ellittiche e quindi i punti cambiano di momento in momento. Le ultime cifre sono perciò del tutto “inutili” in valore assoluto, ma permettono di valutare le differenze tra di loro. Anche la distanza Terra-Sole è approssimata, ma poco importa, vista la variabilità dei punti.  Non dimentichiamo, inoltre, che il problema non è certo di “soli” tre corpi, ma di molti di più. Non si possono, infatti, trascurare le perturbazioni dei pianeti maggiori.

Lo stesso Lagrange non aveva mai creduto che questi punti avessero un significato particolare nell’ambito del Sistema Solare. Oggi, invece, sappiamo che sono estremamente importanti, dato che seppur non fisicamente “immobili”, in essi e nelle loro vicinanze, la risultante delle forze che agiscono su un oggetto è molto piccola. Non per niente, molti telescopi spaziali sono stati inseriti proprio in tali posizioni.

Ad esempio, un oggetto posto in L₁ del sistema Terra-Sole non “subisce” mai il “fastidio” della Terra o della Luna, mentre osserva il Sole. L₂, invece, non è disturbato dalla presenza del Sole e volge le spalle alla Terra. Non è realmente “perfetto”, dato che è più lontano del limite dell’ombra terrestre e quindi riceve parte della radiazione solare. Insomma, vede un’eclissi anulare di Sole permanente. In fondo, però, questo fatto è di una certa utilità per le batterie solari. L3 è importante per studiare la superficie solare prima (o dopo) che ce la mostri direttamente, ma è poco stabile, dato che risente molto di più delle perturbazioni esterne (ad esempio Venere si avvicina fino a 0.3 UA ogni 20 mesi).

Più in generale, ricordiamo ancora che i punti L₁, L₂ e L₃ sono di equilibrio instabile (a differenza di L₄ e L₅). Tuttavia, i telescopi vengono inseriti in orbite attorno a questi punti che possono essere, facilmente, mantenute stabili.

Fermiamoci qui… la prossima volta richiameremo L₄ e L₅ e le superfici equipotenziali di un sistema stellare binario con i suoi lobi di Roche.