Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

 

Prima di iniziare questo articolo, dedicato ai celebri punti lagrangiani, utilissimi sia per le applicazioni pratiche di meccanica celeste, sia per la descrizione fisica dei sistemi binari stretti, fatemi ricordare in modo “realistico” chi era Lagrange e che cosa voleva trovare. Innanzitutto, il vero nome di Lagrange era Giuseppe Luigi De La Grangia ed era italianissimo.

Antipasto storico

Giuseppe Luigi De La Grangia nasce a Torino nel 1736 da famiglia di umili origini. Compie i suoi studi nella stessa città, ma, come spesso capita, la Germania prima e la Francia poi, gli danno la possibilità di essere riconosciuto come uno dei più grandi matematici della storia. A parte i campanilismi, a noi interessa, comunque, una sua fondamentale ricerca, zeppa di risvolti astronomici ancora oggi fondamentali.

Si sa molto bene che mentre è semplice dedurre il moto di un corpo attorno a un altro (problema dei due corpi) o, più esattamente, attorno al comune baricentro, diventa analiticamente impossibile risolvere le equazioni del moto di tre corpi legati gravitazionalmente tra loro. Ancora oggi, per affrontare il problema, sono necessarie integrazioni numeriche e supercomputer in grado di svolgere calcoli di portata spaventosa.

Il nostro De La Grangia aveva cercato una soluzione particolare del problema dei tre corpi, una che gli desse la possibilità di risolverlo matematicamente e che d’altra parte, avesse anche un campo di applicazione molto vasto. La sua ipotesi fu allora quella di considerare la massa del terzo corpo trascurabile rispetto a quella degli altri due. In tale situazione l’equazione del moto aveva alcune particolari soluzioni analitiche perfette.

Vi sembra troppo riduttiva? Nemmeno per sogno. Pensate al moto degli asteroidi e delle comete sotto l’effetto preponderante delle masse del Sole e di Giove o, problema ancora più attuale, al moto dei satelliti artificiali nel sistema Terra-Luna e dei telescopi spaziali nel Sistema Sole-Terra.

De La Grangia non lo sapeva ancora, ma le ripercussioni sui sistemi stellari binari avrebbe permesso a Roche (ne parleremo tra breve) di descrivere la fisica delle binarie semi-staccate e a contatto.

Cosa sono, allora, i punti lagrangiani? Consideriamo un sistema formato da due masse considerevoli e come la loro forza di gravità agisca nei dintorni. Così ad occhio, potremmo facilmente dire che in certe posizioni si sente quasi solo la forza di una delle due masse e in altre quella di entrambe. Per De La Grangia non fu difficile descrivere il campo gravitazionale di tale sistema (due corpi) e poi introdurre un terzo corpo (di massa trascurabile) libero di muoversi in questo campo.

E’ fu anche facile (si fa per dire…) descrivere le superfici equipotenziali, luogo dei punti in cui le forze agenti sul piccolo intruso si equivalevano. In altre parole, superfici che avevano la stessa energia gravitazionale regalatagli dalle forze combinate delle due masse principali.

A De La Grangia interessava, in modo speciale, trovare su queste superfici le posizioni particolari in cui il terzo corpo potesse trovarsi in perfetto equilibrio tra le forze gravitazionali e quella centrifuga , ossia rimanesse immobile rispetto al sistema rotante.

Come si può disegnare questa configurazione? Semplice, considerando le due masse fisse e descrivendo le linee di uguale energia potenziale attorno ad esse. Se, in tutte le posizioni, si introducesse un terzo oggetto in movimento questo descriverebbe una certa traiettoria, a volte attorno a una massa, a volte attorno all’altra, a volte alternando il suo attrattore principale e via dicendo.

Ma a De La Grangia non interessava descrivere tutte le possibili orbite, voleva trovare matematicamente quelle che avrebbero inserito il terzo corpo in una situazione di equilibrio, ossia tale da farlo rimanere immobile rispetto alle altre due masse.

Bene, dopo questo piccolo antipasto, affrontiamo la questione sotto tutti i punti di vista, sia meccanico che fisico ( chi volesse averne un’idea molto approssimata e rapida può leggere questo articolo e chi fosse particolarmente interessato alla Sfera di Hill, quest’altro articolo più tecnico)

Prima, però, è bene ricordare cosa sia veramente il baricentro di un sistema.

Il "capo" dei punti

Abbiamo spesso pensato al campo gravitazionale, generato da una grande massa, come a una enorme ragnatela (QUI), capace di catturare e gestire il moto di un piccolo corpo che gli si avvicini troppo. In parole povere stiamo parlando del problema dei due corpi, discusso non molto tempo fa (QUI). E’ ora di passare a una doppia ragnatela e vedere cosa è capace di fare. Parleremo di baricentro, di punti lagrangiani, di lobi di Roche  e tante belle cose che in parte già sappiamo, ma che è bene riassumere e trattare con maggiori dettagli.

Cerchiamo di costruire questa doppia ragnatela andando avanti a piccoli passi. La faremo girare attorno un punto molto particolare che conosciamo molto bene, ma che è meglio richiamare in modo più “formale”. Detto in altre parole, vogliamo affrontare il problema dei tre corpi, limitandoci alle sue soluzioni più “scaltre”.

Baricentro geometrico

Limitiamoci a un piano (ma non sarebbe difficile lavorare anche nelle tre dimensioni) e consideriamo un sistema di assi cartesiani x,y. Prendiamo un certo numero di punti P_i, individuati ovviamente dalle loro coordinate x_i,y_i, come mostrato in Fig. 1.

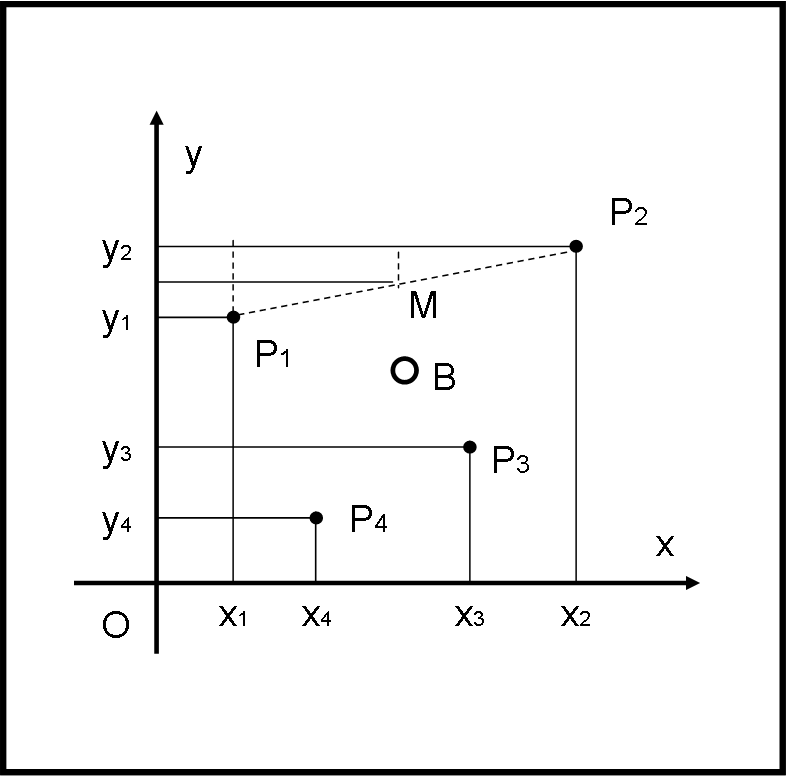
Ricordiamo, prima di tutto, cosa significa punto medio tra due punti o -se preferite- punto medio del segmento che unisce due punti. Sia esso, ad esempio il segmento P₁P₂. Beh, penso proprio che tutti sappiano che basta fare la media delle x e delle y e il punto, che ha come coordinate questi valori medi, è proprio il punto medio M. E’ la stessa cosa che si fa quando ci si chiede : “Qual è il valore medio tra 2 e 5?”. Non si fa altro che sommare i due numeri e dividere per due, ossia:

(2 + 5)/2 = 3.5

Nel caso di due punti basta allora fare la media delle loro x e delle loro y, ossia:

x_M = (x₁ + x₂)/2

y_M = (y₁ + y₂)/2

E’ immediato estrapolare il concetto a n punti, così come è immediato calcolare la media di n numeri… “Qual è il valore medio di  sei numeri come 2, 4, 8, 9, 14, 17 ?”. Ovvio:

(2 + 4 + 8 + 9 + 14 + 17)/6 = 44/6 = 7.3333…

Basta sommare i numeri e dividere per il loro numero totale.

Passando, allora al nostro piano cartesiano, basta scrivere (in modo generalizzato e per n punti qualsiasi):

x_B = (x₁ + x₂ + x₃ + …. + x_n)/n

y_B = (y₁ + y₂ + y₃ + …. + y_n)/n

Per passare allo spazio a 3 dimensioni basterebbe aggiungere:

z_B = (z₁ + z₂ + z₃ + …. + z_n)/n

In modo più compatto (ormai lo conosciamo bene dalle lezioni di matematica (QUI))

x_B = Σⁿ_{i = 1} x_i/n

y_B = Σⁿ_{i = 1} y_i/n

Questo punto B(xB,yB) viene chiamato baricentro geometrico dell’insieme di punti P_i.

Centro di massa

Per restare in campo matematico, potremmo adesso ragionare in un modo molto semplice. Consideriamo i numeri 1, 2, 4 e 5 (tanto per fare un esempio). Tuttavia, nella nostra serie di dieci numeri totali, qualcuno compare più di una volta. Il 2 compare due volte, il 4 due volte e il 5 cinque volte. Il valore medio diventa, perciò:

(1 + (2 + 2) + (4 + 4) + (5 + 5 + 5 + 5 + 5))/10 =  3.8

Potremmo anche scrivere:

(1 + 2(2) + 2(4) + 5(5))/10 = (1 + 4 + 8 + 25)/10 = 3.8

In parole molto semplici, abbiamo eseguito una media pesata. Ossia, se un certo numero o punto compare più volte, esso viene moltiplicato per il numero di volte che compare e poi si esegue la somma dividendo per il numero totale effettivo dei punti.

Ad esempio, passando al piano cartesiano, potremmo avere 3 volte il punto P₁(x₁,y₁), due volte il punto P₂ (x₂,y₂) e 5 volte il punto P₃(x₃,y₃). In totale 10 punti.

Sarebbe inutile sommare x₁ tre volte, x₂ due volte e x₃ cinque volte, basterebbe moltiplicare x₁ per 3, x₂ per 2 e x₃ per 5 e poi dividere per 10, ossia:

x_B = (3x₁ + 2x₂ +5x₃)/10

y_B = (3y₁ + 2y₂ +5y₃)/10

In poche parole, abbiamo ottenuto un baricentro diverso da quello dato dai tre punti P₁, P₂ e P₃, presi singolarmente, dato che ogni punto compare un certo numero di volte, ossia con un certo PESO.

Il nome “peso” ci aiuta a passare a un baricentro ben più importante, di tipo fisico, detto anche centro di massa.  Basta scrivere:

x_B = m₁x₁ + m₂x₂ + m₃x₃ + … + m_nx_n/(m₁ + m₂ + m₃ + … + m_n)

y_B = m₁y₁ + m₂y₂ + m₃y₃ + … + m_ny_n/(m₁ + m₂ + m₃ + … + m_n)

e, invece di vedere m_i come il numero di volte che compare un certo valore x_i (o y_i), si può pensare a m_i come alla massa del punto P_i.

Il baricentro o centro di massa di n oggetti puntiformi di massa diversa è dato quindi dalle relazioni:

x_B = Σⁿ_{i = 1} m_ix_i/M

y_B = Σⁿ_{i = 1} m_iy_i/M

dove M è la massa totale dei punti, ossia:

M = Σⁿ_{i = 1} mi

Due sole masse

Nel moto dei tre corpi, vi sono due masse che dominano la situazione, mentre la terza è considerata trascurabile, ne segue che il baricentro o centro di massa del sistema formato da due masse m₁ e m₂ si riduce semplicemente alle relazioni:

x_B = (m₁x₁ + m₂x₂)/(m₁ + m₂)

y_B = (m₁y₁ + m₂y₂)/(m₁ + m₂)

Se consideriamo le due masse poste lungo l’asse x (possiamo sempre sceglierlo in questo modo), la relazione si riduce alla prima delle due equazioni precedenti.

x_B = (m₁x₁ + m₂x₂)/(m₁ + m₂)

Possiamo trafficare un po’ con questa relazione…

x_B (m₁ + m₂) = m₁x₁ + m₂x₂    …. (1)

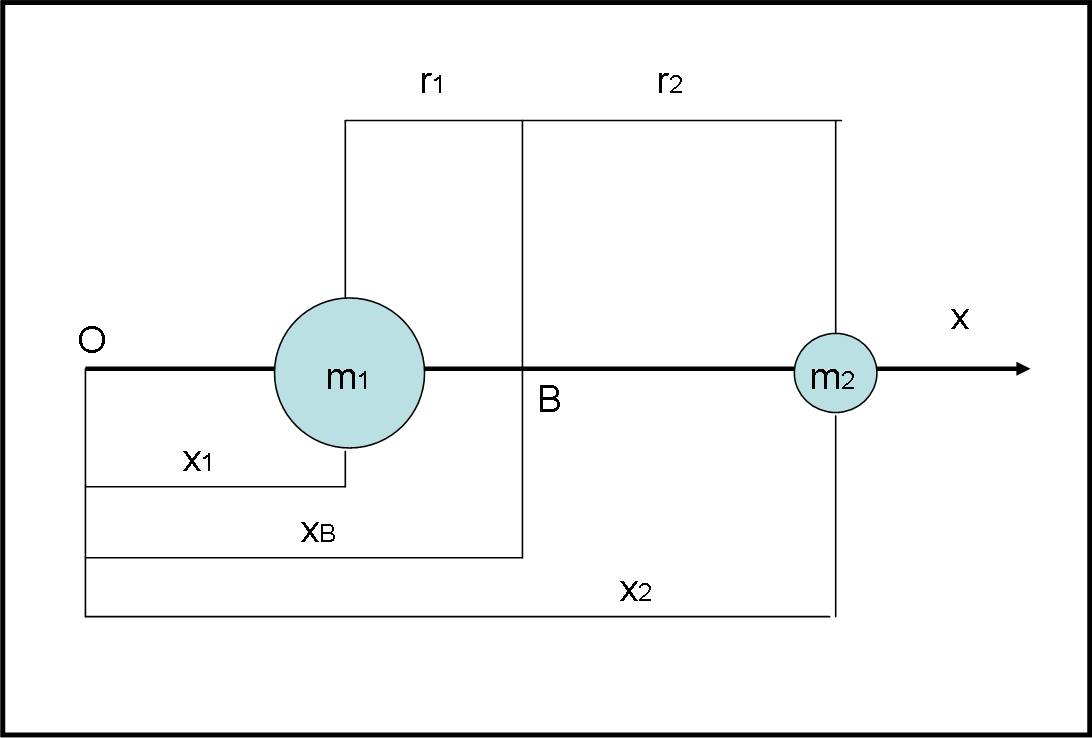
A questo punto, chiamiamo r₁ la distanza tra il punto P₁ e il centro di massa e r₂ la distanza tra il punto P₂ e il centro di massa. La Fig. 2 ci dice subito (avendo scelto un certo verso positivo) che:

x₁ = x_B - r₁

x₂ = x_B + r₂

Sostituendo nella (1)

x_B (m₁ + m₂) = m₁ (x_B  - r₁) + m₂ (x_B + r₂) = x_B(m₁ + m₂) - m₁r₁ + m₂r₂

semplificando:

- m₁r₁ + m₂r₂ = 0

m₁r₁ = m₂r₂

r₁/r₂ = m₂/m₁

che è la formula più conosciuta per definire il baricentro tra due masse distinte. Essa dice, in pratica, che la distanza dal centro di massa o baricentro dalle due masse è inversamente proporzionale ad esse. Il che vuole anche dire che più una massa è grande rispetto all’altra e più il baricentro del sistema si avvicina alla prima. Ad esempio, nel caso del Sole e della Terra, il baricentro cade all’interno della superficie del Sole.

Un po’ di vettori e un piccolo QUIZ grafico

La trattazione fatta finora ha fatto uso di coordinate cartesiane, ma, in generale, può essere più utile e “fisico” considerare le distanze vettoriali r_i dei punti rispetto a una certa origine O (x_i, y_i sono le sue componenti), come mostrato in Fig. 3.

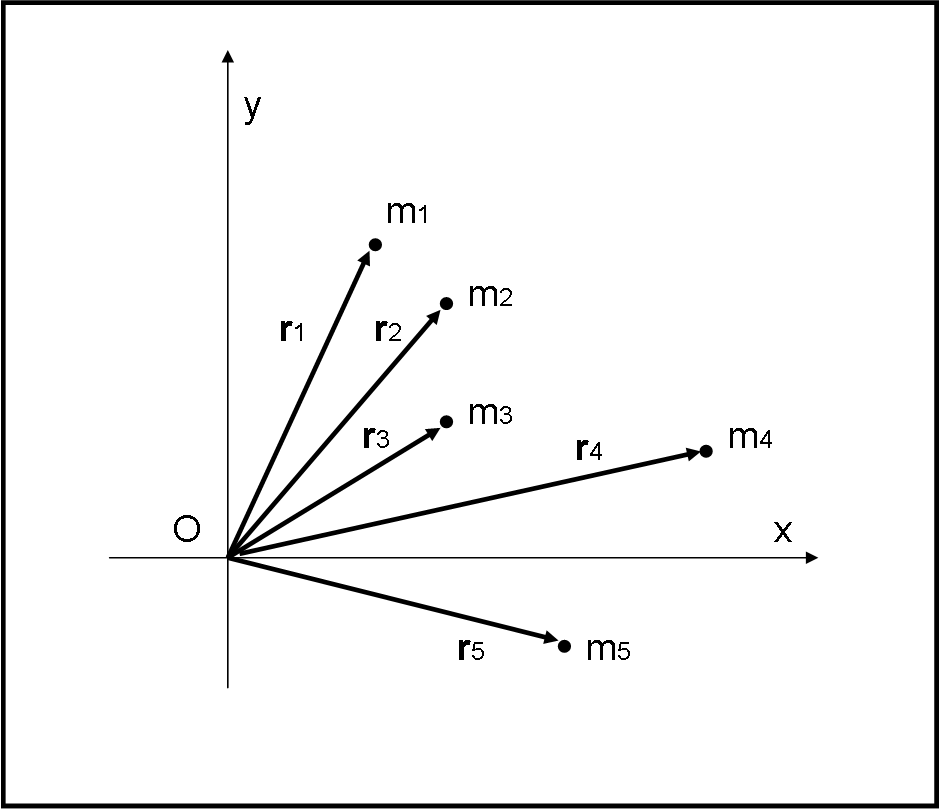
In tal modo è molto semplice e intuitivo calcolare la somma delle singole masse moltiplicate per i relativi vettori posizione r_i: essa non è altro che una somma vettoriale che si risolve con il metodo del parallelogramma (QUI), applicato via via a tutti i vettori. Immaginiamo, ad esempio, che le masse siano tutte uguali a uno. I  moduli dei singoli vettori sono, perciò, esattamente uguali alle distanze tra origine e punto finale P_i. La formula che dona la posizione del centro di massa diventa:

r_B = Σⁿ_{i = 1} r_i/n

La massa M diventa, ovviamente, 1 x n = n (numero di punti)

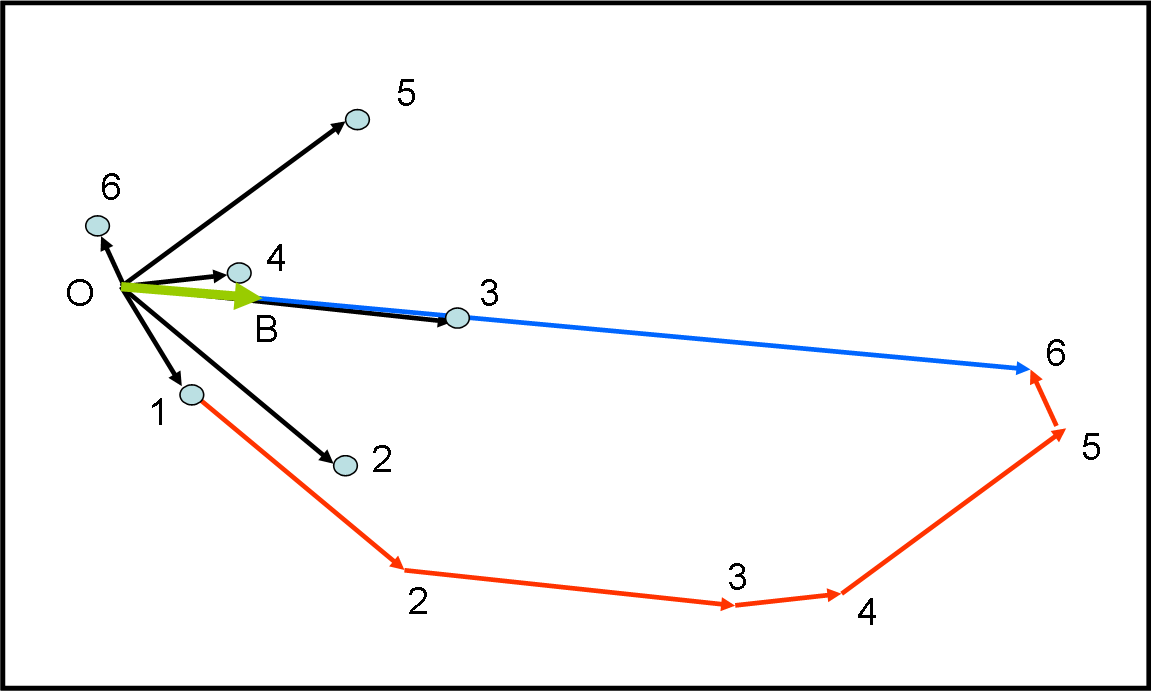
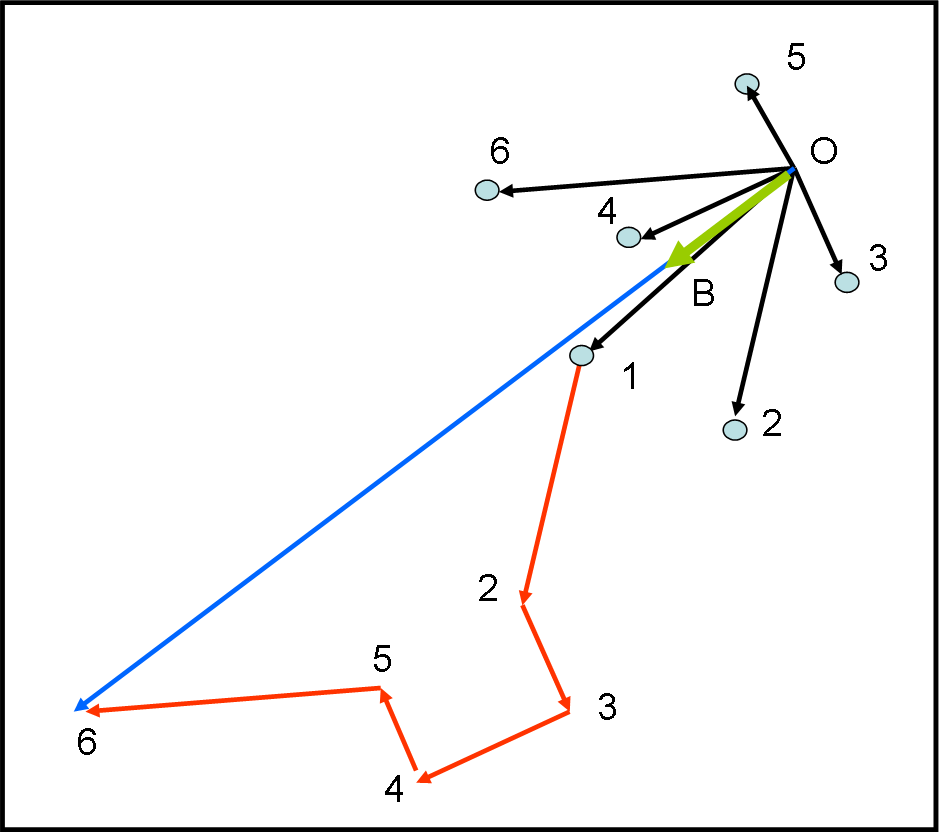
Vediamo un esempio grafico in Fig. 4. Sono stati disegnati sei punti di massa unitaria. Domanda: Come fareste a trovare vettorialmente e soltanto graficamente il loro baricentro, nel modo più rapido? Notate che non ho imposto nessuna origine…

La risposta è piuttosto semplice. Si può prendere un'origine qualsiasi (il risultato non cambia assolutamente) e si tracciano tutti i vettori che uniscono l'origine con i punti della Fig. 4. Graficamente, è molto semplice calcolare il vettore SOMMA: lasciamo fermo il primo e spostiamo tutti gli altri in modo che la loro "coda" coincida con la "testa" di quello precedente. Come già sappiamo dallo studio dei vettori, il vettore somma è quello che unisce l'origine con l'ultima "testa", come rappresentato in Fig. 4bis e 4ter. Il modulo del vettore somma (blu) deve essere diviso per sei (numero dei punti) e si ottiene il vettore verde che indica il baricentro B.  Pur cambiando origine O il risultato è lo stesso!

Oggetto rigido esteso: un po’ di integrali

L’importanza del baricentro risulta -forse- ancora più chiara quando si parla di un oggetto rigido esteso. Ricordiamo, ad esempio, che tutta la massa può essere considerata concentrata nel suo baricentro (QUI).

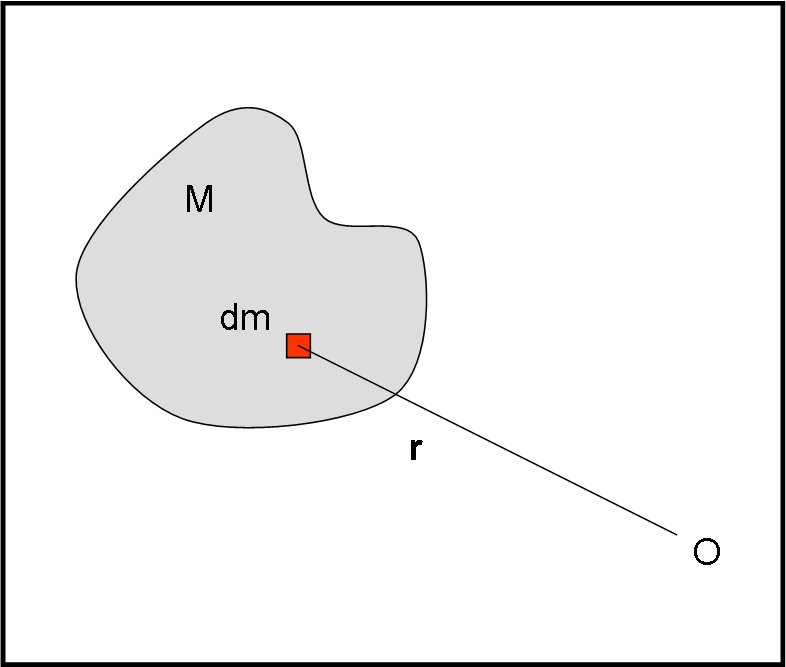
Questa affermazione ci porta automaticamente a definire il baricentro di un oggetto qualsiasi (non puntiforme). Basta dividere l’oggetto in tanti “pezzettini” di massa infinitesima dm e poi sommare tutte le masse, moltiplicate per il vettore posizione relativo, e dividerle per la massa totale (Fig. 5).

Per fare questo speciale tipo di somma ci viene in aiuto l’operazione di integrale (QUI).

In pratica, vengono considerati tanti volumetti dV che, considerando la densità δ costante, permettono di scrivere la massa dm come:

dm = δ dV

e, quindi, la somma di tutte le masse, moltiplicate per i vettori posizione, risulta:

δ ∫_V r dV

mentre  la massa totale è:

δ ∫_V dV

Ne segue che:

r_MB= ∫_V r dV/∫_V dV = ∫_V r dV/V

Ovviamente, la scelta della forma dei “pezzettini” di volume dV dipende molto dalla forma dell’oggetto in generale. Ma questo è tutto un altro discorso… dato che se la figura è piana useremo un integrale doppio e se è a tre dimensioni, un integrale triplo…

Concludiamo, cercando di analizzare la differenza, se esiste, tra baricentro e centro di massa. Entrambi sono caratteristiche intrinseche dell’oggetto (o dell’insieme di punti), indipendenti da dove l’oggetto sia posizionato. Il baricentro di un gruppo di punti o di una figura geometrica dipende solo dalla dislocazione dei punti o dalla forma. Il centro di massa vede comparire la massa, assegnata a ogni punto o all’oggetto esteso. In entrambi i casi, se la densità è costante, tutto si riduce a un calcolo puramente geometrico. Baricentro e centro di massa sono del tutto equivalenti.

Baricentro fisico

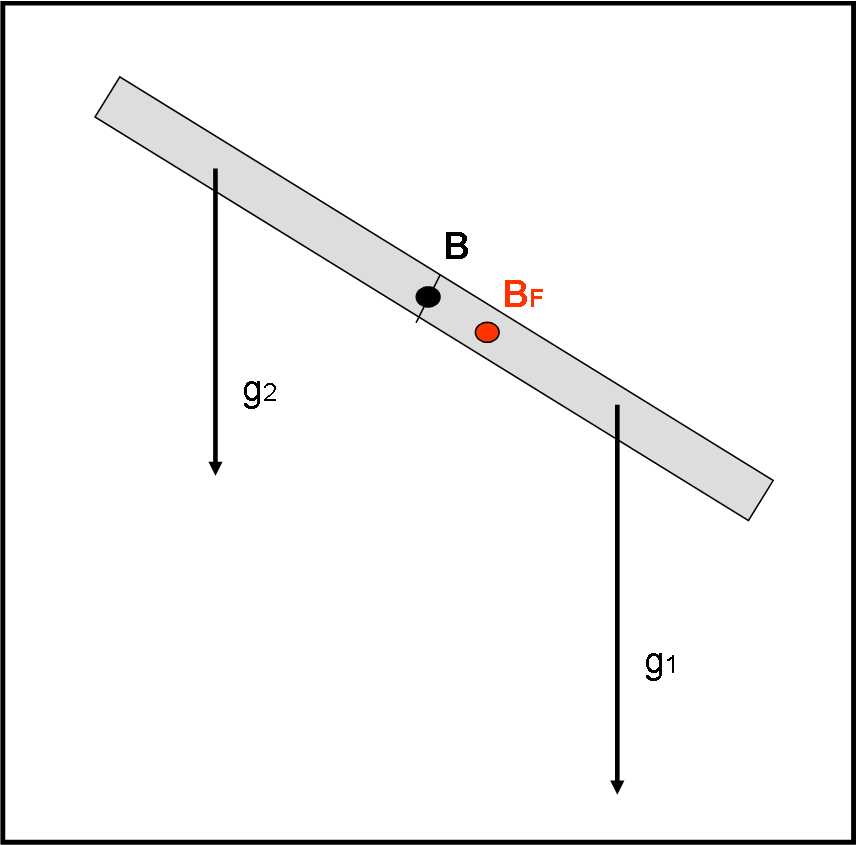
Tuttavia, se un corpo viene immerso in un campo di forze come, ad esempio, quella gravitazionale, può succedere che l’oggetto in questione sia disposto in modo tale che i suoi “punti” subiscano una forza peso diversa.

Immaginiamo una barra di ferro omogenea che cada verso la Terra, inclinata di un certo angolo rispetto alla verticale. Una sua parte subisce una gravità minore dell’altra e quindi il baricentro fisico si sposta verso la parte che avanza (vedi Fig. 6) e non coincide più con il centro di massa che deve rimanere sempre lo stesso, essendo una caratteristica intrinseca dell’oggetto. Tuttavia, questa situazione non ha veri risvolti pratici e possiamo, perciò, fare coincidere la definizione di baricentro con quella di centro di massa (sempre che la densità sia costante).

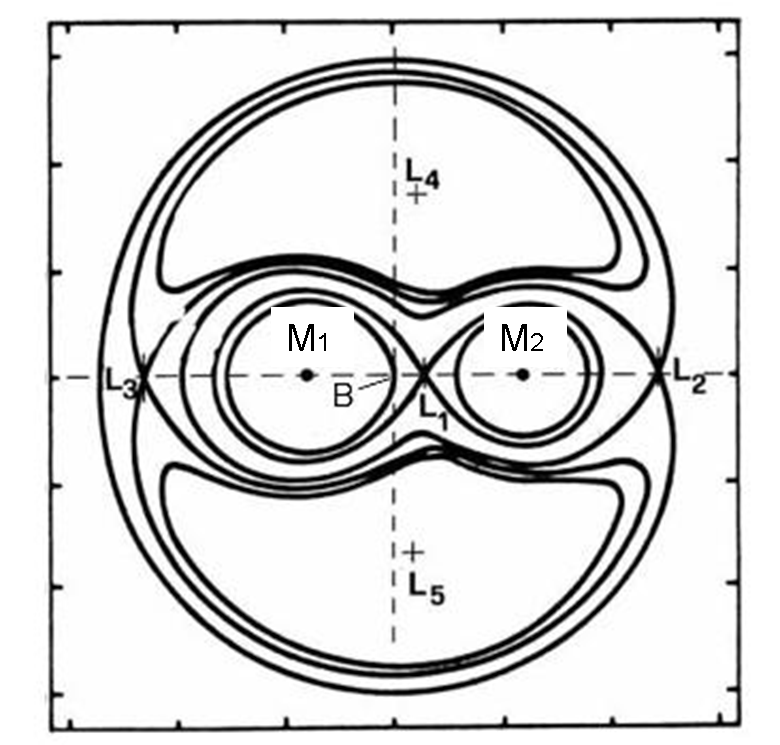
L’argomento baricentro non finisce certo qui, dato che la possibilità di concentrare tutta la massa di un corpo in questo punto veramente speciale permette di usarlo, come punto di riferimento fondamentale, nella descrizione dei vari moti. Ricordiamo, ad esempio, come il baricentro di un sistema stellare doppio si muova di moto rettilineo uniforme, mentre le stelle gli danzano intorno. Proprio a una situazione simile dobbiamo riferirci per parlare dei punti lagrangiani e di L4 e L5, in particolare.

I punti lagrangiani L1, L2 e L3

Il problema di base sembrerebbe piuttosto semplice, dato che nasce dal classico e generale problema “dei tre corpi”. Esso chiede soltanto, date due masse orbitanti attorno al comune baricentro, di descrivere il moto di un terzo oggetto che si trovi immerso nel campo gravitazionale degli altri due.

Bene, questo è un problema che è analiticamente irrisolvibile e si riesce a descrivere solo attraverso iterazioni successive e semplificazioni varie. In poche parole, il terzo corpo dovrebbe anch’egli rivolvere attorno al baricentro del sistema, ma nel far ciò è disturbato dalle forze di gravitazione delle due masse principali che variano da punto a punto.

Il modo più semplice per trattare il problema, come già detto, è quello di considerare la massa del terzo corpo del tutto trascurabile rispetto alle altre due. Anche così, però, le cose non sono certamente semplici. Esistono, tuttavia, cinque punti estremamente particolari: essi rimangano FERMI rispetto al sistema in rotazione. In altre parole, se ci poniamo nel sistema che ruota, vedremo questi punti sempre nella stessa posizione rispetto alle due masse che “costruiscono” il campo gravitazionale. Succede, praticamente, quello che ci mostra l’animazione di Fig. 7.

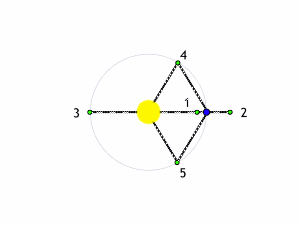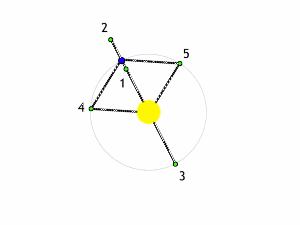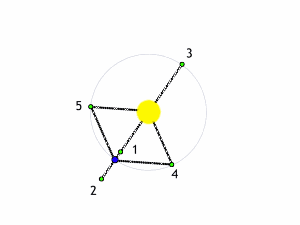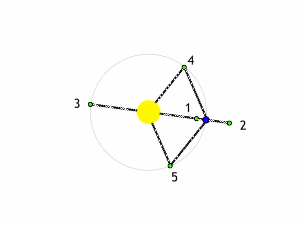
E’ facile capire come questi punti, di origine puramente teorica, abbiano ripercussioni pratiche enormi, dato che se al posto delle due masse consideriamo la Terra e il Sole, ad esempio, essi rappresentano posizioni ideali per osservare diversi oggetti celesti, dato che caso per caso non vengono disturbati dal moto relativo della Terra e del Sole. Tutto è infatti immobile, in perfetto equilibrio.

Prima di iniziare, diciamo subito che dei cinque punti, due (L₄ e L₅) sono posti ben al di fuori della congiungente Terra-Sole. Li conosciamo già molto bene e li tratteremo più tardi. Occupiamoci, per adesso, di L₁, L₂ e L₃ che si trovano tutti allineati tra loro. Disegniamo la Fig. 8 che illustra perfettamente il problema, le distanze e le forze in gioco.

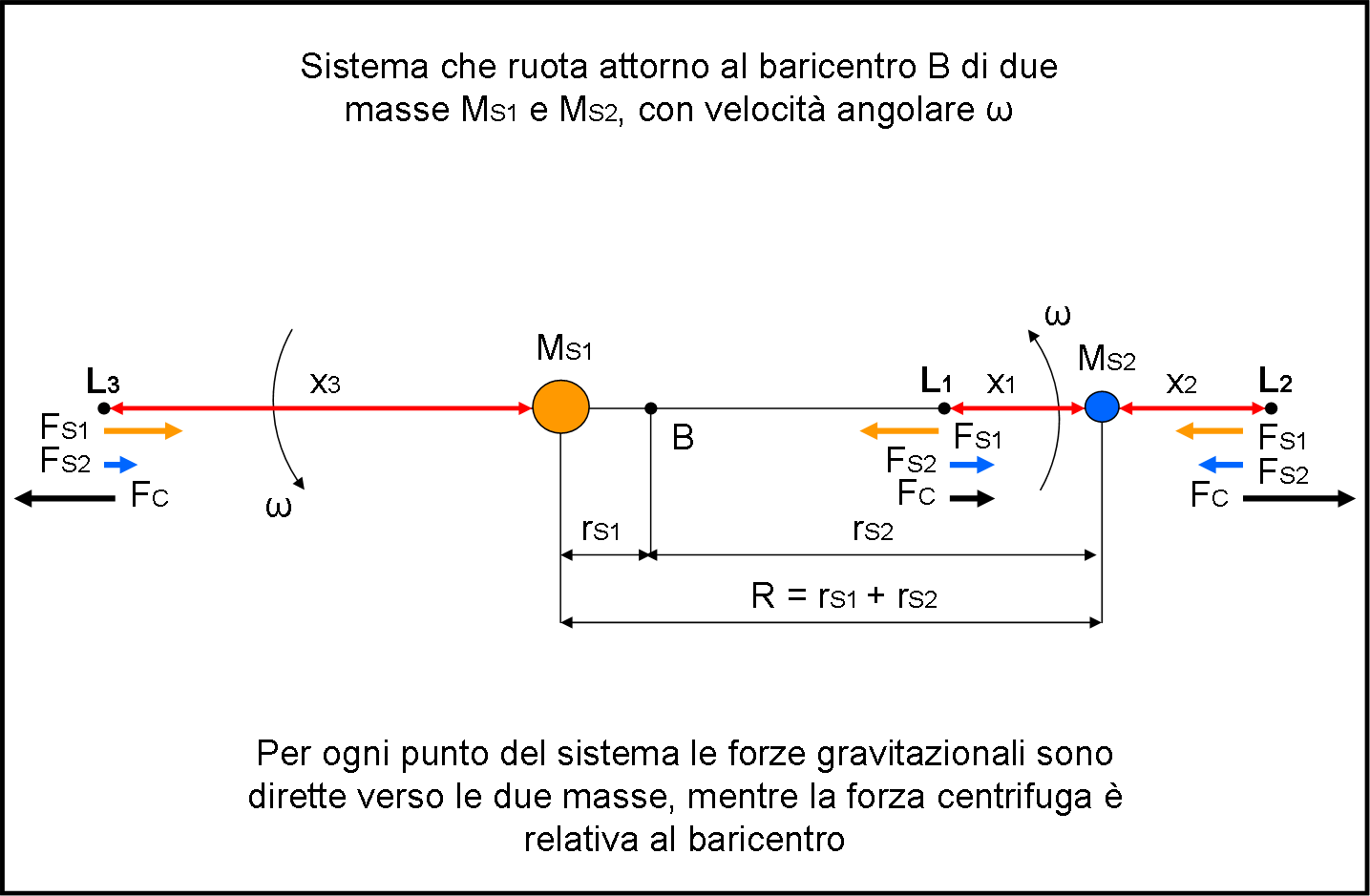
M_S1 e M_S2 sono le masse dei due corpi principali che ruotano attorno al comune baricentro B  con velocità angolare ω. L₁, L₂ e L₃ sono i tre punti lagrangiani, dove, come già detto, le forze gravitazionali delle due masse principali vengono controbilanciate dalla forza centrifuga. Vediamo cosa succede, caso per caso.

Un oggetto posto in L₁ orbita in una posizione più vicina a M_S1  di quella di M_S2 . Dovrebbe, perciò, avere un periodo di rivoluzione più corto (terza legge di Keplero). Tuttavia, non si può ignorare l’effetto gravitazionale dovuto a M_S2 . Se l’oggetto si trova nella direzione M_S1 -M_S2 , la forza di  M_S2 controbilancia in qualche modo la forza gravitazionale del corpo di massa M_S1  e allunga il periodo orbitale dell’oggetto. Più si avvicina a M_S2  e più l’effetto cresce. Nel punto L₁ il periodo orbitale diventa esattamente uguale a quello dell’oggetto di massa M_S2 , anche se le loro posizioni non coincidono.

Dalla parte opposta della massa M_S2 , il periodo orbitale è invece più lungo di quello di M_S2 . Tuttavia, la forza gravitazionale di M_S2  si somma a quella di M_S1 , accorciando il periodo orbitale fino a che, in L₂, esso uguaglia nuovamente quello di M_S2 .

L₃, invece, si trova dalla parte opposta di M_S1 , su un’orbita appena più larga di quella di M_S1 , ma più vicina a M_S1  di quanto non sia M_S2 . Quanto detto non è un’assurdità, dato che le orbite si compiono attorno al baricentro di M_S1  e M_S2 . La somma delle forze gravitazionali di M_S1  e M_S2  porta l’oggetto in L₃ a ruotare con lo stesso periodo di M_S2 .

Normalmente, M_S2 è decisamente minore di M_S1 (Terra-Sole, Luna-Terra)

Come si intuisce molto bene, per descrivere i tre punti è necessario fare agire tre forze: quelle gravitazionali di M_S1  e M_S2  e quella centrifuga che deve controbilanciarle. In particolare: In L₁ abbiamo un forza F_S1 maggiore di quella F_S2 e di verso opposto. La risultante deve essere uguale e contraria alla forza centrifuga F_C agente in quel punto. In L₂ e L₃ le due forze gravitazionali si sommano e la somma deve essere uguale e contraria alla forza centrifuga.

Non ci resta, quindi, che scrivere per esteso queste tre relazioni, chiamando x₁, x₂ e x₃ le distanze dei punti lagrangiani dalla massa M_S2 (i primi due) e da M_S1 (il terzo). R è la distanza tra le due masse e r_S1 e r_S2 sono le distanze delle due masse dal comune baricentro. Ovviamente, poniamo tutte le orbite circolari, altrimenti le cose si complicherebbero enormemente, dato che varierebbero costantemente le distanze relative e quindi anche le posizioni dei punti lagrangiani. Fidatevi di me: basta e avanza!

Le tre equazioni sono :

L₁

F_S1 = F_S2 + F_C       …. (1)

L₂

F_S1 + F_S2 = F_C       …. (2)

L₃

F_S1 + F_S2 = F_C       …. (3)

Veramente banali… a prima vista.

Per esprimere la forza centrifuga agente su una massa m, basta ricordare che:

F_C = mrω²

Nel caso della massa M_S2, ad esempio, questa forza deve bilanciare esattamente la forza gravitazionale di M_S1 agente su M_S2. Ricordiamo che la forza di gravità dipende dalla distanza tra le due masse, mentre la forza centrifuga è riferita al baricentro del sistema. Si ha, quindi:

F_C = M_S2r_S2 ω² = GM_S1M_S2/R²

Da cui

ω² = GM_S1/r_S2R²    …. (4)

Però, si può anche scrivere:

F_C = M_S1r_S1ω² = GM_S1M_S2/R²

Da cui

ω² = GM_S2/r_S1R²    …. (5)

In poche parole, possiamo esprimere la velocità angolare in funzione delle masse M_S1 e M_S2 e della distanza tra le due masse dal baricentro. Tenendo conto che la velocità angolare deve essere la stessa anche per l’oggetto di massa m posto in L₁, L₂ e L₃, abbiamo che la forza centrifuga per i tre punti diventa:

L₁

Usando la (4)

F_C = m(r_S2 - x₁)ω² = GmM_S1(r_S2 – x₁)/r_S2R²

L₂

Usando la (4)

F_C = m(r_S2 + x₂)ω² = GmM_S1(r_S2 + x₂)/r_S2R²

L₃

Usando la (5)

F_C = m(r_S1 + x₃)ω² = GmM_S2(r_S1 + x₃)/r_S1R²

Tutto bene fin qui? Direi di sì… abbiamo solo sostituito una velocità angolare costante all’interno delle forze centrifughe corrispondenti ai singoli punti di equilibrio.

Passiamo ora a scrivere le forze gravitazionali delle due masse M_S1 e M_S2 agenti sui tre punti lagrangiani:

L₁

F_S1 = GmM_S1/(R - x₁)²

F_S2 = GmM_S2/x₁²

L₂

F_S1 = GmM_S1/(R + x₂)²

F_S2 = GmM_S2/x₂²

L₃

F_S1 = GmM_S1/x₃²

F_S2 = GmM_S2/(R + x₃)²

Utilizzando la Fig. 2 è proprio un gioco da bambini!

Siamo pronti, adesso, a scrivere per esteso le equazioni (1), (2) e (3)

F_S1 = F_S2 + F_C

GmM_S1/(R - x₁)² = GmM_S2/x₁² + GmM_S1(r_S2 – x₁)/r_S2R²            …. (1)

F_S1 + F_S2 = F_C

GmM_S1/(R + x₂)² + GmM_S2/x₂² = Gm M_S1 (r_S2 + x₂) /r_S2R²        …. (2)

F_S1 + F_S2 = F_C

GmM_S1/x₃² + GmM_S2/(R + x₃)² = Gm M_S2 (r_S1 + x₃) /r_S1R²        …. (3)

Che si semplificano dato che Gm appare in tutti i termini

M_S1/(R - x₁)² = M_S2/x₁² + M_S1(r_S2 – x₁)/r_S2R²          …. (1)

M_S1/(R + x₂)² + M_S2/x₂² = M_S1 (r_S2 + x₂) /r_S2R²         …. (2)

M_S1/x₃² + M_S2/(R + x₃)² = M_S2 (r_S1 + x₃) /r_S1R²       …. (3)

Perfetto! Veramente semplice.

Abbiamo tre equazioni in cui l’unica incognita è, per ognuna di esse, x₁, x₂ e x₃, rispettivamente. Infatti, le masse dei due corpi principali sono note, così come la loro distanza e quella dal baricentro. Non ci resta che risolvere, una per una, le equazioni e trovare, rispettivamente, x₁, x₂ e x₃.

Provate, provate pure… ma vi consiglio di desistere subito…

Ognuna di loro è un’equazione di quinto grado! Non ci credete? Provate a ridurle allo stesso denominatore. Nel primo caso esso diventa: (R - x₁)² x₁² r_S2R². Il numeratore del terzo termine deve, perciò, essere moltiplicato per (R - x₁)² x₁² e, quindi, diventa M_S1(r_S2 – x₁) (R - x₁)² x₁². Come volevasi dimostrare: la x₁ compare alla quinta potenza!

La soluzione dell’equazione diventa un’operazione non certo banale e si ottiene attraverso vari “trucchi” sia grafici che di interazioni successive. Delle cinque soluzioni, bisogna scegliere quella “buona”, ossia per L₁, ad esempio, quella che cade tra 0 e 1. in termini di distanza tra M_S1 e M_S2.

A titolo di esempio riportiamo i valori dei tre punti lagrangiani nei sistemi Sole-Terra e Terra-Luna.

Sole-Terra (R = 149.600.000 km)

x₁ = 1.501.557 km

x₂ = 1.491.557 km

x₃ = 149.599.737 km

Terra-Luna (R = 384.401 km)

x₁ = 64.499 km

x₂ = 58.006 km

x₃ = 381.678 km

I valori riportati sono valori medi, dato che le orbite sono ellittiche e quindi i punti cambiano di momento in momento. Le ultime cifre sono perciò del tutto “inutili” in valore assoluto, ma permettono di valutare le differenze tra di loro. Anche la distanza Terra-Sole è approssimata, ma poco importa, vista la variabilità dei punti.  Non dimentichiamo, inoltre, che il problema non è certo di “soli” tre corpi, ma di molti di più. Non si possono, infatti, trascurare le perturbazioni dei pianeti maggiori.

Lo stesso De La Grangia (Lagrange) non aveva mai creduto che questi punti avessero un significato particolare nell’ambito del Sistema Solare. Oggi, invece, sappiamo che sono estremamente importanti, dato che seppur non fisicamente “immobili”, in essi e nelle loro vicinanze, la risultante delle forze che agiscono su un oggetto è molto piccola. Non per niente, molti telescopi spaziali sono stati inseriti proprio in tali posizioni.

Ad esempio, un oggetto posto in L₁ del sistema Terra-Sole non “subisce” mai il “fastidio” della Terra o della Luna, mentre osserva il Sole. L₂, invece, non è disturbato dalla presenza del Sole e volge le spalle alla Terra. Non è realmente “perfetto”, dato che è più lontano del limite dell’ombra terrestre e quindi riceve parte della radiazione solare. Insomma, vede un’eclissi anulare di Sole permanente. In fondo, però, questo fatto è di una certa utilità per le batterie solari. L3 è importante per studiare la superficie solare prima (o dopo) che ce la mostri direttamente, ma è poco stabile, dato che risente molto di più delle perturbazioni esterne (ad esempio Venere si avvicina fino a 0.3 UA ogni 20 mesi).

Più in generale, ricordiamo ancora che i punti L₁, L₂ e L₃ sono di equilibrio instabile (a differenza di L₄ e L₅). Tuttavia, i telescopi vengono inseriti in orbite attorno a questi punti che possono essere, facilmente, mantenute stabili.

E adesso sotto con L₄ e L_5.

I punti lagrangiani L₄ e L₅

Questo articolo è un piccolo capolavoro di logica ed eleganza (non certo per merito mio…). Vi invito a leggerlo senza paura. Esso presenta la determinazione dei punti lagrangiani L₄ e L₅, nel modo più generale possibile, seguendo la strategia illustrata nel 1999 da I. Vorobyov dell’Università di Vienna. Un metodo di una semplicità disarmante, che io ho solo cercato di arrangiare in modo veramente elementare (matematica e geometria delle scuole medie).

 

Come abbiamo già detto varie volte, i punti lagrangiani, da un punto di vista fisico, sono strettamente collegati alle superfici equipotenziali di due corpi rotanti, ossia la ormai famosa doppia ragnatela, di cui parleremo nell’ultima parte. Essi sono gli unici cinque punti di equilibrio del sistema rotante: un oggetto posto in uno di essi, mantiene una posizione fissa rispetto alle due masse predominanti. Il sistema di riferimento in cui definirli è, perciò, quello rotante. Le forze in gioco sono, di conseguenza, quelle attrattive delle masse e quella centrifuga.

I punti L₁, L₂ e L₃ sono, in qualche modo, “facilitati” (QUI), dato che sono situati lungo la retta che unisce le due masse. Gli ultimi due, invece, si trovano ben distanti da questa linea e nemmeno De La Grangia stesso avrebbe mai pensato che la sua soluzione matematica potesse avere una conferma fisica, data dai celebri asteroidi troiani e greci di Giove. Non solo i punti esistono e sono stabili, ma sono anche occupati fisicamente da corpi celesti in carne e ossa (ops… in terra e ghiaccio).

Prima di passare alla determinazione a cui si accennava prima, possiamo facilmente dimostrare che, effettivamente, la posizione ai vertici di un triangolo equilatero (in cui due vertici sono occupati dalle masse M₁ e M₂) soddisfa le condizioni richieste. Tuttavia, è una soluzione “di comodo”, perché non ci dice se possono esistere altri punti con le stesse caratteristiche.

Consideriamo la Fig. 9 in cui abbiamo disegnato due masse M₁ e M₂ e una piccola massa m posta proprio in modo da formare un triangolo equilatero con le altre due.

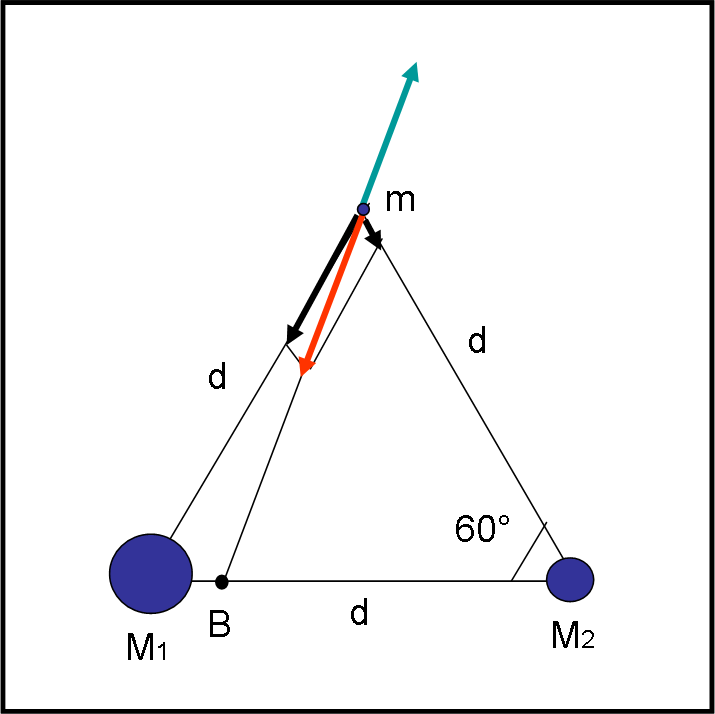
La massa m è attratta da entrambe e si trova alla stessa distanza da loro. Le forze agenti su di lei sono, perciò, direttamente proporzionali alle due masse M₁ e M₂. Ne segue che la composizione delle due forze è diretta verso il baricentro B. Dato che il sistema ruota attorno a B, la forza centrifuga che agisce sulla massa m controbilancia l’attrazione gravitazionale, assicurando la stabilità della posizione. Questa è però una dimostrazione “ a posteriori”. Inoltre, è ben chiaro che abbiamo considerato un sistema del tutto particolare, in cui il centro di massa stia sulla congiungente le due masse M₁ e M₂.

E se le tre masse fossero comparabili? In realtà, la soluzione visualizzata comunemente per i punti L₄ e L₅ si riferisce quasi sempre al caso di Giove e del Sole, in cui il baricentro è praticamente coincidente con quest’ultimo. Una figura ormai di uso comune… ma la configurazione può essere molto più generale ed è interessantissimo seguirne la trattazione, che è poi quella proposta e risolta dallo stesso De La Grangia. Penso che anche i più esperti la troveranno illuminante e -forse- inaspettata.

Al di là dell’interesse matematico e fisico del risultato, seguiamola passo dopo passo per renderci conto di come si possano spiegare concetti anche difficili attraverso una serie di passaggi logici veramente elementari, a patto che vi sia dietro un cervello brillante. L’equazione “grande intelligenza = grande complessità” non è assolutamente obbligatoria (Feynman insegna). Come dicevo, il merito va tutto a Vorobyov e alla sua genialità: io ho solo cercato di semplificare e rendere ancora più immediata la trattazione, per renderla veramente godibile a TUTTI, amanti e non amanti della matematica.

Consideriamo tre corpi di massa m₁, m₂ e m₃ (la generalizzazione è massima) che NON stiano sulla stessa linea, ma che rivolvano con la stessa velocità angolare attorno a un certo punto O, su circonferenze ovviamente concentriche (il centro è lo stesso…). La situazione, mostrata in Fig. 2, simula perfettamente quella di un corpo “solido” che ruoti attorno a un asse, un corpo formato da un centro e da tre “barre” fisse che lo colleghino alle tre masse o, se preferite, un triangolo qualsiasi che giri attorno a un punto interno.

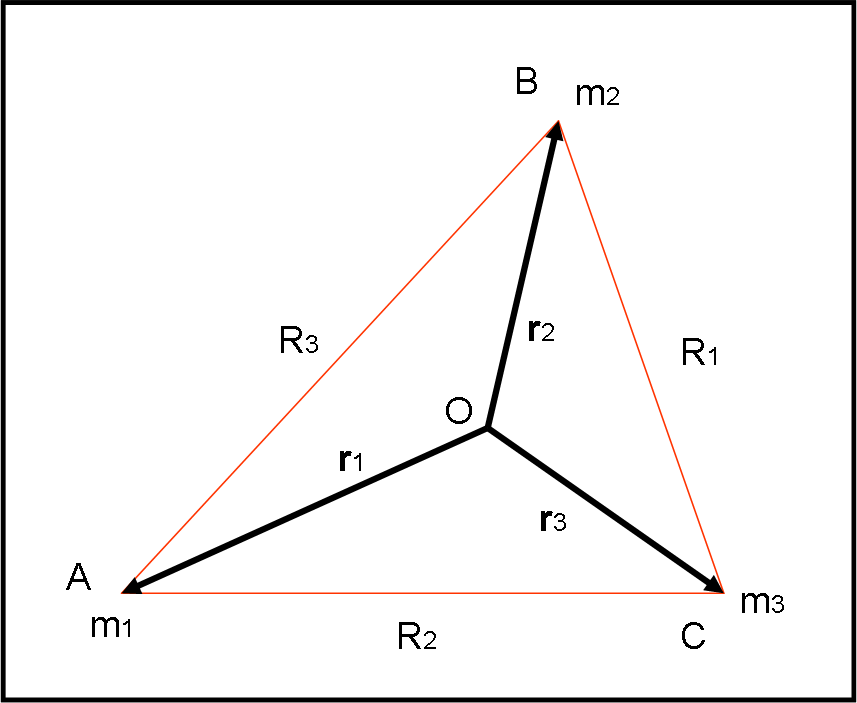
Ci chiediamo: “E’ possibile questa configurazione? E, se sì, sotto quali condizioni?”

Nel sistema rotante ciascuna massa m_i deve rimanere in equilibrio. In poche parole, vogliamo che il triangolo non muti la sua forma durante la rotazione.

Ogni singolo corpo è soggetto alle forze attrattive degli altri due corpi. Esse sono date da:

F₁ = F₁₂ + F₁₃

F₂ = F₂₃ + F₂₁

F₃ = F₃₁ + F₃₂

In parole povere, abbiamo solo detto che la forza attrattiva che subisce ogni massa m_i è la somma delle forze attrattive che m_j e m_k esercitano su di lei (sono ovviamente somme vettoriali). Tutte queste forze F_ij sono ovviamente dirette lungo i lati  R_k corrispondenti,

Il modulo della generica forza vale (legge di gravitazione di Newton):

│F_ij│= G m_im_j/R_k²                  (modulo della generica forza F_ij)

I tre corpi, però, devono anche ruotare con la stessa identica velocità angolare ω attorno a O. Sono perciò soggetti alle forze centrifughe F_Ci (dirette secondo OA, OB, e OC) date da (QUI):

F_C1 = m₁ω²r₁

F_C2 = m₂ω²r₂                  …. (1)

F_C3 = m₃ω²r₃

Ogni corpo deve essere in equilibrio nel sistema rotante, ossia la somma di tutte le forze agenti su di esso deve essere uguale a ZERO, ossia:

F₁ + F_C1 = 0

F₂ + F_C2 = 0

F₃ + F_C3= 0

O, ancora:

F₁₂ + F₁₃ + F_C1 = 0

F₂₃ + F₂₁ + F_C2 = 0

F₃₂ + F₃₁ + F_C3 = 0

Sommando le tre equazioni, si ha:

F₁₂ + F₁₃ + F₂₃ + F₂₁ + F₃₂ + F₃₁ + F_C1 + F_C2 + F_C3 = 0

Tuttavia, per il terzo principio della dinamica, si ha:

F₁₂ = - F₂₁

F₁₃ = - F₃₁

F₂₃ = - F₃₂

Abbiamo solo scritto che se m_i agisce su m_j con una certa forza gravitazionale, m_j deve agire su m_i con una forza uguale e contraria.

Semplificando si ha:

F_C1 + F_C2 + F_C3 = 0

Ricordando le (1)

m₁ω²r₁ + m₂ω²r₂ + m₃ω²r₃ = 0

Dato che ω non può essere uguale a zero, possiamo scrivere:

m₁r₁ + m₂r₂ + m₃r₃ = 0            …. (2)

Ricordando la definizione di baricentro o centro di massa, rispetto a una certa origine O (QUI):

r_B = Σ³_{i = 1} m_ir_i/M

si ha che se r_B = 0, come dice la (2), il punto O deve essere il baricentro del sistema delle tre masse m₁, m₂ e m₃.

In realtà, questo risultato non fa altro che confermare che, se in un sistema di corpi le uniche forze sono quelle che si esercitano tra di essi, il baricentro deve rimanere fisso. Ossia, il punto O, attorno a cui avviene la rivoluzione dei tre corpi, non può muoversi e quindi DEVE essere il baricentro del sistema.

Appurato questo fatto importantissimo, possiamo passare alla seconda parte dell’articolo, dove traffichiamo un po’ con i vettori. La figura di riferimento è adesso la Fig. 3 che è uguale a quella precedente, tranne qualche piccola freccetta. Notiamo che i vettori R₂ e R₃ puntano entrambi verso m₁

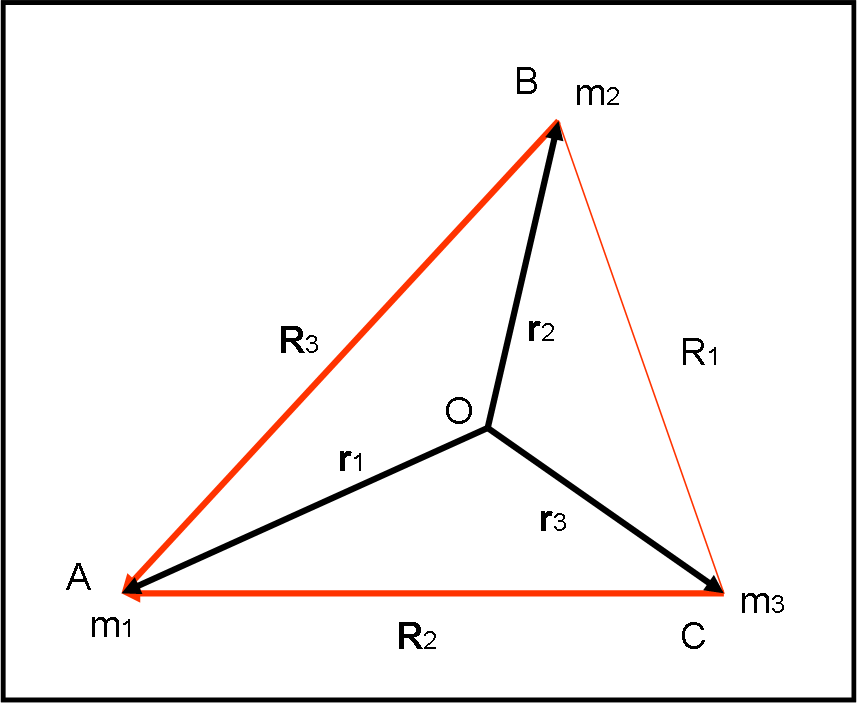
Sappiamo benissimo come sommare dei vettori, quindi non vi è nessun problema a scrivere:

r₁ = r₂ + R₃

ma anche:

r₁ = r₃ + R₂

Moltiplichiamo la prima equazione per m₂, la seconda per m₃ e poi le sommiamo :

m₂r₁ + m₃r₁ = m₂r₂ + m₂R₃ + m₃r₃ + m₃R₂        …. (3)

Dalla (2) abbiamo:

m₂r₂ + m₃r₃ = - m₁r₁

Sostituendo nella (3):

m₂r₁ + m₃r₁ = m₂R₃ + m₃R₂ - m₁r₁

m₂r₁ + m₃r₁ + m₁r₁= m₂R₃ + m₃R₂

r₁(m₁ + m₂ + m₃) = m₂R₃ + m₃R₂

Da cui si ricava:

r₁ = (m₂R₃ + m₃R₂)/(m₁ + m₂ + m₃)

Adesso, facciamo bene attenzione. Il vettore r₁ è la somma di due vettori, ossia:

ρ₂ = m₃ R₂/(m₁ + m₂ + m₃)

e

ρ₃ = m₂ R₃/(m₁ + m₂ + m₃)

In modo compatto:

r₁ = ρ₂ + ρ₃

Ragioniamo sopra questo semplice, ma fondamentale risultato.

Innanzitutto, si può affermare che ρ₂ ha la stessa direzione di R₂ così come ρ₃ ha la stessa direzione di R₃. I vettori differiscono, infatti, solo per il modulo. Inoltre, la somma vettoriale di ρ₂ e ρ₃ deve proprio essere r₁. Ne segue che i due nuovi vettori possono essere indicati facilmente in blu nella Fig. 12.

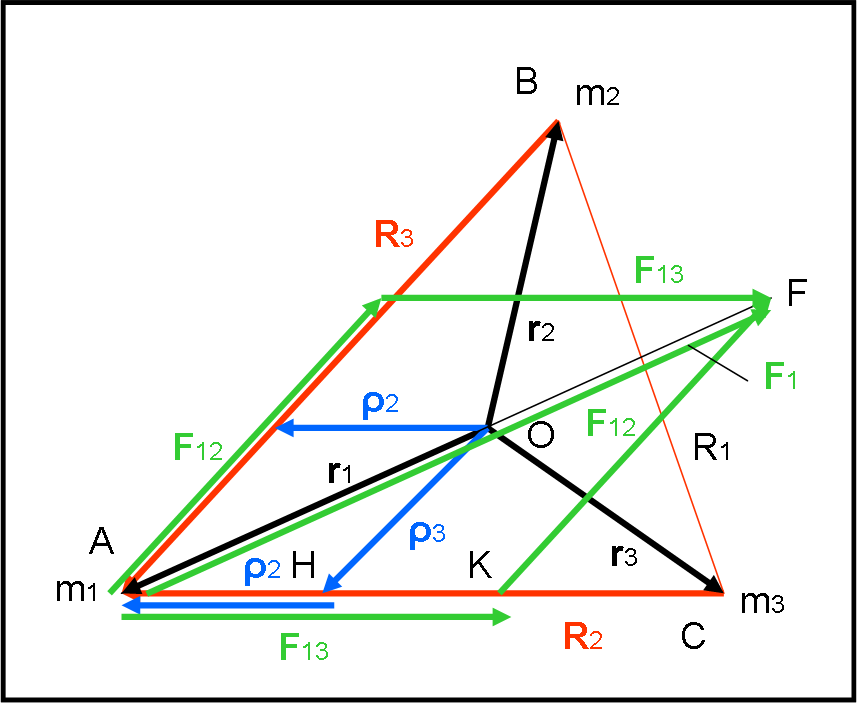
Ora viene la parte più “astuta”.

Passiamo ai vettori delle forze gravitazionali agenti su m₁. La forza F₁₂ (relativa a m₂) deve agire lungo il lato R₃. La forza F₁₃ (relativa a m₃) deve agire lungo il lato R₂. In altre parole, le due Forze sono parallele ai vettori ρ₃ e ρ₂. Disegniamo queste due forze, F₁₂ e F_13, in verde.  Il modulo possiamo anche disegnarlo a caso (dipende dalle masse), ma è sicuramente vero che la risultante F₁ delle due forze F₁₂ e F_13, deve essere diretta da m₁ verso il baricentro (il moto avviene attorno a lui).

Consideriamo i triangoli AOH e AFK. Essi sono simili (i tre angoli sono uguali).

I loro lati, però, sono proprio i vettori forze F₁₂ e F₁₃ e i vettori ρ₃ e ρ₂. Ne segue che i loro moduli devono essere in proporzione:

F₁₂/ρ₃ = F₁₃/ρ₂

Scrivendoli per esteso:

Gm₁m₂/R₃²: m₂R₃/(m₁ + m₂ + m₃) = Gm₁m₃/R₂²: m₃ R₂/(m₁ + m₂ + m₃)

(Gm₁m₂/R₃²) (m₃ R₂/(m₁ + m₂ + m₃)) = (Gm₁m₃/R₂²) (m₂R₃/(m₁ + m₂ + m₃))

Gm₁m₂m₃ R₂/ R₃² (m₁ + m₂ + m₃) = Gm₁m₃ m₂ R₃/R₂² (m₁ + m₂ + m₃)

Semplificando:

R₂/R₃² = R₃/R₂²

R₂³ = R₃³

Ossia:

R₂ = R₃

Se qualcuno vuole divertirsi, può rifare l’ultima parte di calcolo cambiando la massa di riferimento: invece di m₁ si può considerare m₂, con tutti i vettori relativi. Troverà, ovviamente, che:

R₁ = R₃.

Il triangolo ABC deve essere equilatero e O ne è il baricentro.

Alla domanda iniziale: “E’ possibile questa configurazione? E, se sì, sotto quali condizioni?”, possiamo rispondere senza esitazione: “Sì, la configurazione è possibile a patto che il centro di rotazione O sia il baricentro del sistema e che le tre masse occupino i vertici di un triangolo equilatero”.

Notiamo molto bene quanto la soluzione sia ben più generale di quella che viene comunemente riportata. Le tre masse sono qualsiasi e il triangolo ruota attorno al baricentro del sistema.

I troiani e i greci di Giove si trovano (quasi) esattamente nei pressi dei punti lagrangiani L₄ e L₅. In realtà, le loro orbite librano attorno a questi punti, in modo anche vistoso, ma il sistema complessivo mantiene la sua stabilità perfetta.

Questo classico esempio è, però, estremamente particolare. Il baricentro O coincide praticamente con il Sole e, di conseguenza, il pianeta e i due gruppi di asteroidi rivolvono attorno al Sole lungo la stessa orbita (Fig. 13).

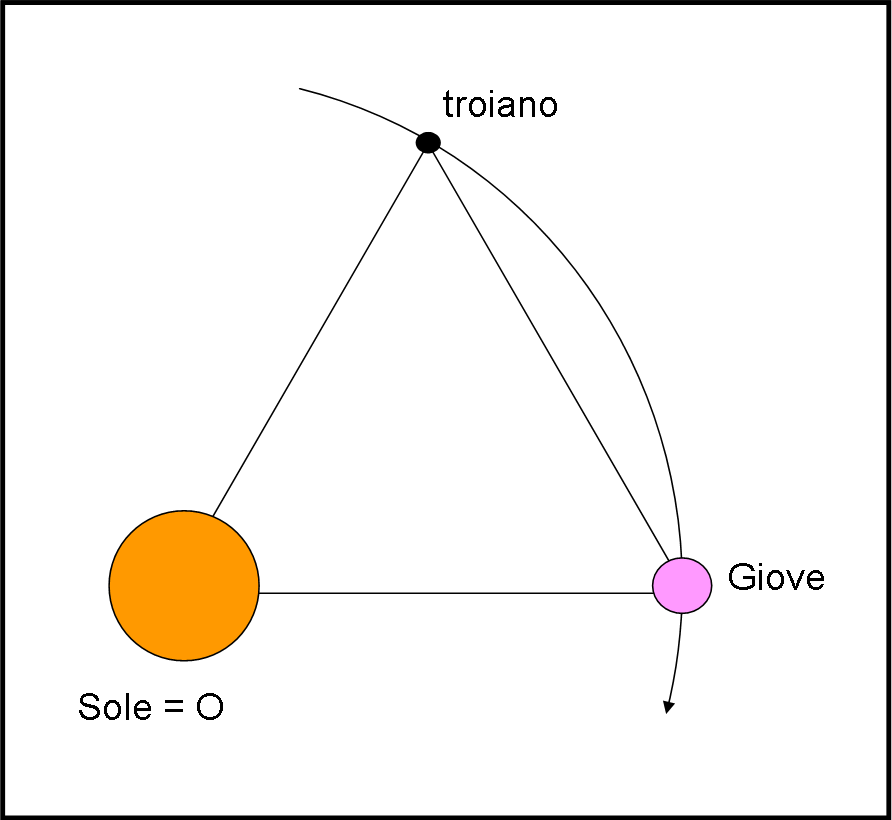
Chissà che, prima o poi, non si trovi un sistema stellare triplo che rappresenti l’esempio più generale della geniale soluzione (particolare) di De La Grangia, per il problema dei tre corpi…

Esistono anche altri metodi per determinare L₄ e L₅, soprattutto analitici. Essi sono estremamente “noiosi” e contorti. Ho preferito presentare solo quello vettoriale, molto più semplice e geniale.

La doppia ragnatela e i lobi di Roche

La parte che segue, da un punto di vista fisico, doveva, forse, essere trattata per prima. Poco male, dato che le informazioni ci sono, comunque, tutte. Ciò che diremo è in parte già stato affrontato in varie occasioni e in particolare nell’articolo dove si era definito il campo gravitazionale di una singola massa, la famosa ragnatela (QUI). Aggiungiremo anche, per i meno preparati, qualche discorso sull’energia meccanica. Poi finalmente ci dedicheremo alla doppia ragnatela … energetica che permette un’applicazione diretta e insostituibile ai sistemi binari stretti, uno degli argomenti più caldi  e fondamentali dell’evoluzione stellare.

Andiamo avanti con ordine, cercando di definire al meglio i parametri coinvolti. Per far ciò avremmo, in realtà, bisogno di descrivere buona parte della Meccanica, ma cercheremo di limitarci ai concetti fondamentali che qua e là abbiamo già usato e descritto. Per chi volesse una visione generale e completa, non posso che far riferimento al libro “La Fisica addormentata nel Bosco”. Tuttavia, dato che la mia “bontà” è ormai qualità ben nota a tutti (ah ah ah…), inseriamo una trattazione molto elementare e abbastanza completa dedicata all’energia, una delle grandezze più importanti e più ambigue dell’Universo (del cui principio di conservazione QUI abbiamo dato una spiegazione-favola adatta a grandi e piccoli)

La ragnatela gravitazionale

Un piccolo richiamo... Nell'articolo sulla ragnatela singola, siamo stati capaci di eliminare la massa della particella  e trattare le caratteristiche  solo sulla base della massa centrale .

Non abbiamo fatto altro che confermare ciò che Galileo sapeva benissimo: la cinematica dei corpi che vengono intrappolati nella ragnatela non dipende assolutamente dalla massa della preda. In parole ben più note: una sfera di cotone e una di piombo cadono al suolo con la stessa velocità.

Torniamo, allora, al nostro campo gravitazionale e vediamo di raddoppiarlo, ossia mettiamo quasi a contatto due ragni con le loro ragnatele. Purtroppo, esse si “mescolano”, creando una configurazione piuttosto intricata. Per studiarla al meglio utilizziamo la nostra massa unitaria e vediamo cosa le può succedere.

A ogni punto da lei occupato viene associato un vettore (una lezione sui vettori la trovate QUI), di intensità uguale all’accelerazione di gravità, comandata dalla forza di gravità, diretto verso il centro della stella. Il suo valore lo conosciamo molto bene:

a_G = GM/r²

Se la ragnatela fosse unica, avremmo una situazione molto semplice come quella di Fig. 14.

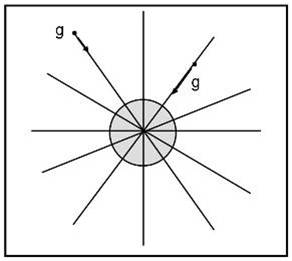
Il problema è che adesso i ragni sono due e due sono le loro trappole, sovrapposte tra loro. Calma e sangue freddo. Cerchiamo di ricordare cosa sono le linee di forza di un campo gravitazionale. Esse sono le linee che congiungono la massa unitaria e la massa centrale (il ragno). In altre parole, sono le linee che la massa seguirebbe se fosse lasciata in balia della ragnatela. Nel caso della singola ragnatela, queste linee sono ovvie e vengono descritte dalle rette disegnate in Fig. 14. Le linee di forza e loro tangenti sono la stessa cosa, ma possiamo anche concludere che i vettori accelerazione gravitazionale sono in ogni punto tangenti alle linee di forza.

Se i ragni sono due, non ci resta che valutare le accelerazioni di gravità delle due masse-ragni in modo indipendente e poi sommare i due vettori. Quello finale è l’accelerazione dovuta a entrambe le ragnatele e la linea di forza corrispondente non sarà altro che la curva tangente alla retta in quel punto. Lavorando in questo modo, la ragnatela finale, dovuta all’intersezione delle due ragnatele, si costruisce con grande semplicità come rappresentato in Fig. 15.

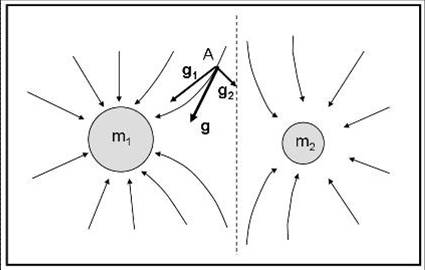
Le linee di forza non sono più semplici come prima. La motivazione è ovvia: i due campi gravitazionali si sovrappongono. I punti più critici sono quelli vicini al limite tra le due ragnatele (linea tratteggiata). Nel caso della figura, la massa m₁ è maggiore di m₂ e quindi un punto posto a pari distanza dalle due masse-ragni, tende a cadere verso la più massiccia (l’accelerazione di gravità cresce con la massa che l’esercita).

Se il punto è in una certa posizione tra le due stelle la situazione diventa “imbarazzante”. Imbarazzante, nel senso che il punto ha un grande imbarazzo su dove cadere… rimane più o meno in sospeso in una sorta di equilibrio. Ma andiamo con calma e non crediamo di essere già arrivati ai punti lagrangiani. Ci siamo, infatti, dimenticati che le due masse ruotano attorno al proprio baricentro (appena trattato) e le condizioni di equilibrio diventano una cosa ben più complicata Soprattutto, pensiamo che l’applicazione all’evoluzione stellare ha bisogno di qualcosa di più fisico.

Dobbiamo fermarci qui e prendere una decisione. Passare subito alle superfici equipotenziali o introdurre con molta calma una grandezza fisica di importanza veramente unica: l’energia. Solo lei, infatti, permette di delineare una situazione che abbia applicazioni veramente “pratiche” nei casi di due masse molto vicine. E’ vero, la conosciamo bene e l’abbiamo usata molto spesso, ma -forse- senza che tutti i lettori possano veramente darle del “tu”.

Per alcuni, quindi, la parte che viene inserita adesso è solo un piccolo ripasso, ma per altri può essere utile per chiarire concetti non sempre completamente digeriti. Avete già capito che ho deciso di partire proprio dall’inizio e i più preparati non se ne abbiano a male e saltino pure i prossimi capitoli (ma so che non lo faranno…).

Una definizione quasi impossibile

Cari amici, se c’è una cosa difficile da definire in fisica è proprio la sua attrice più importante: l’energia.

Ricordate il vecchio cartone animato di Walt Disney “La Spada nella Roccia”? Vi è la celebre battaglia tra Maga Magò e Mago Merlino. Le armi che usano sono quelle della trasformazione. La prima cerca di diventare sempre più grande e spaventosa, il secondo sempre più piccolo e apparentemente inoffensivo. Ancora una volta vincerà il microcosmo… ma a noi interessa il fatto che la capacità di agire e di vincere si basa sull’abilità di trasformarsi senza mai perdere la propria efficacia globale.

Ebbene, l’energia è qualcosa del genere. Permette di agire, ma si trasforma continuamente e la sua stessa definizione diventa sfuggente e ambigua. Quanto lo sia in realtà ce lo ha mostrato la dinamica relativistica (QUI), ma le cose non sono da meno anche nella fisica classica. In questo caso, possiamo eliminare qualche problema, trattando solo con l’energia meccanica, quella che ci serve in prima approssimazione. L’energia, allora, ha solo due possibilità di trasformazione: energia cinetica ed energia potenziale. Per la nostra trattazione semplificata bastano e avanzano.

Tentiamo allora una definizione estremamente tecnica che è più che sufficiente allo scopo. Iniziamo con l’energia cinetica, la più immediata e banale.

L’energia di chi si muove

Tutte le volte che una forza agisce, provocando lo spostamento di un corpo, compie un lavoro. quest’ultimo necessita di una certa capacità intrinseca. Questa capacità rappresenta l’energia, ossia la capacità di un corpo di compiere lavoro. In altre parole, a ogni corpo che sta compiendo un lavoro, sotto l’azione di una forza, è associata una proprietà, che chiamiamo energia.

Ancora più semplicemente: il lavoro svolto per spostare un corpo da una posizione a un’altra rappresenta un qualcosa acquistato dal corpo, una specie di “riserva”. La forza ha trasmesso al corpo la capacità di compiere un lavoro.

Usiamo ancora qualche frase, specifica per l’energia cinetica, per cercare di chiarire al massimo il concetto: quando un corpo di massa m acquista una certa velocità o la varia per effetto di una forza,  esso acquista o varia la sua energia cinetica. Il lavoro rappresenta questa variazione di energia cinetica. L'energia cinetica è, quindi, associata alla massa e alla velocità di un corpo in movimento.

Il lavoro compiuto sulla massa si è trasformato in energia cinetica. All’istante zero e con velocità zero, il corpo non ne ha, ma alla fine del lavoro la possiede ed è proprio uguale al lavoro eseguito.

Ovviamente, se il corpo si ferma di nuovo, la sua energia cinetica torna a zero. Ha dovuto compiere un lavoro negativo e spendere l’energia che aveva acquisito.

Esiste quindi energia cinetica solo quando il corpo è in movimento. Se il movimento si effettua a velocità costante, anche l’energia cinetica rimane costante e, quindi, il corpo non compie lavoro (la forza è nulla). Questo concetto è estremamente importante e non banale come sembra. Tenetelo bene a mente.

In altre parole, ancora, l'energia cinetica di un corpo è il lavoro necessario per portarlo da una velocità iniziale a una velocità finale. Questo lavoro è immagazzinato nel corpo come energia, che rimane in attesa di essere sfruttata o cambiata in un'altra o spesa completamente.

Qualcuno dirà: “Ma il lavoro cos’è?”. Beh… ne abbiamo già parlato, ma è meglio richiamarlo in modo molto sintetico. Il lavoro è il prodotto tra la forza e lo spostamento che ha causato, nella direzione della forza. In parole povere è (in modulo):

L = F s

Ormai conosciamo gli integrali (articolo 51 e seguenti delle lezioni di matematica) e prendiamo spunto da questo richiamo per descrivere in modo formale il teorema delle forze vive o dell’energia cinetica, che dice soltanto (!) ciò che abbiamo appena detto: l'energia cinetica di un corpo è il lavoro necessario per portarlo da una velocità iniziale ad una velocità finale (il lavoro è una differenza di energia, quella finale e quella iniziale).

Consideriamo uno spostamento infinitesimo ds che comporti un lavoro infinitesimo dL

dL = F ds = (dq/dt)ds                        (non potevo dimenticare la “mia” quantità di moto…).

dL = (ds/dt) dq = v d(mv) = m vdv     ( m è costante in fisica classica…)

Integrando su un intervallo AB si ha:

L = m ∫_B^A v dv = m[v²/2] _A^B = ½ mv²_B – ½ mv²_A

Se il corpo parte da fermo, v_A = 0 e il lavoro compiuto è proprio l’energia cinetica posseduta dal corpo.

Divertiamoci con una mela

Proviamo, adesso, a lanciare una pallina (o -meglio- una mela…) verso l’alto. Per lanciarla si deve applicare una forza F alla mela e, quindi, una certa velocità v₀. Questo fatto vuol dire che al momento della partenza l’energia cinetica E_C0 della mela è:

E_C0 = ½ mv₀²

Subito dopo il lancio (la forza non agisce più) la velocità della mela è costretta a diminuire, dato che deve combattere contro la velocità di segno opposto dovuta alla forza peso. La mela, per un po’ continua a salire, ma prima o poi arriva a un’altezza h in cui si ferma. In quel momento qual è l’energia cinetica della mela? Beh, non è difficile calcolarla: dato che v = 0, anche lei deve essere uguale a zero.

Questo vuole anche dire che per passare da terra all’altezza massima la forza applicata alla mela ha svolto un certo lavoro, dato dalla differenza di energia cinetica, ossia:

L = 0 - ½ mv₀².

Un lavoro ovviamente negativo. Quale forza l’ha compiuto? L’unica presente durante il moto: la forza peso, ossia P = mg. Non per niente è negativo: lo spostamento è stato effettuato in senso opposto alla forza.

L’energia iniziale (cinetica) è stata spesa per arrivare fino ad h. A questo punto, però, la mela comincia a cadere trasportata verso il suolo, sempre dalla forza peso. Essa riacquista velocità e lo spostamento avviene nel senso della forza, che, quindi, svolge, finalmente, un lavoro positivo. Quando tocca terra qual è la velocità della mela? Proprio uguale a -v₀. Ne consegue che l’energia cinetica finale è nuovamente

E_CF = ½ m v₀²

La forza peso ha eseguito un lavoro che è dato dalla differenza tra l’energia cinetica finale (quando la mela tocca terra) e quella che aveva all’altezza h.  Ossia è adesso uguale a L = ½ m v₀² – 0.  In altre parole, il lavoro totale compiuto dalla forza peso è stato nullo. Durante tutto il percorso, inoltre, l’energia cinetica è sicuramente cambiata, ma, alla fine, è tornata quella iniziale.

Tuttavia, se è comprensibile la salita della mela in quanto possiede una certa energia di movimento alla partenza, lo è molto meno la discesa. La mela, infatti, quando passa da h al suolo, passa da un’energia cinetica uguale a zero a un’energia cinetica finale diversa da zero. Ciò vuole anche dire che la mela deve avere “creato” una qualche altra forma di energia al momento in cui ha iniziato la caduta. E questa energia non è certo di movimento, dato che la mela parte da ferma. Come per magia alla fine si è ricreata l’energia cinetica iniziale. Sarà forse merito di Maga Magò o di Mago Merlino? No,l’energia si è solo trasformata.

Ricapitolano la situazione: l’energia cinetica è sparita creando un’altra energia che nella caduta si è nuovamente trasformata in energia cinetica. In altre parole, mentre l’energia cinetica passa da un valore massimo a zero, l’altra energia passa da zero a un valore massimo. Nella discesa è avvenuto il contrario, la nuova energia torna  a zero mentre l’energia cinetica torna al valore massimo iniziale. Ma è stata proprio l’energia cinetica che ha “creato” questa nuova energia?

Assolutamente NO!

Basta prendere la mela e farla cadere da una certa altezza h. In questo caso, non esiste alcuna energia cinetica iniziale (la velocità è zero) e quindi non può essere lei a “creare” la nuova energia. Eppure esiste, dato che la mela inizia a cadere e alla fine possiede l’energia cinetica del caso precedente.

L’energia di chi sta fermo

Vedendo le cose in questo modo, possiamo dire che è stata una nuova energia a creare l’energia cinetica finale, un’energia legata solo e soltanto alla posizione del corpo, in particolar modo alla sua altezza h.

Una energia di posizione che prende il nome di energia potenziale, ossia un’energia che esiste in potenza nei corpi e che può dare origine a un lavoro. Dato che essa è sempre e comunque relativa alla forza peso, ossia alla forza di gravitazione, la possiamo chiamare energia potenziale gravitazionale e la indichiamo con U.

Riassumendo: l’energia cinetica esiste solo quando un corpo è in moto, mentre l’energia potenziale anche quando il corpo è fermo.

Facciamo attenzione che nel caso della mela che sale e scende, l’unica forza che agisce dopo il lancio è la forza di gravità (forza peso nel caso di movimenti molto piccoli vicino alla Terra, dove l’accelerazione di gravità può essere considerata costante e uguale a g). Entrambe le energie sono dovute a lei, sia quella che la fa cadere (energia potenziale), sia quella che possiede quando tocca il suolo (energia cinetica).

Quanto vale questa nuova energia in termini di gravità? Basta considerare il lavoro svolto per portare la mela da un altezza h₀ (livello del suolo) a un’altezza h . Esso è dato dal prodotto tra la forza (gm) e lo spostamento (h – h₀). Il lavoro deve essere anche uguale alla differenza di energia potenziale U tra l’istante finale e iniziale.

L =  gmh  - gmh₀ = U – U₀

Se poniamo uguale a zero l’altezza al livello del suolo, l’energia relativa vale zero e si trova:

U = gmh

Attenzione! Notate che abbiamo considerato il suolo come livello per cui h₀ = 0. Una scelta che abbiamo potuto compiere in quanto abbiamo sempre a che fare con differenze di energia potenziale (h e il suolo, oppure tra due diverse altezze). Ma anche perché g è considerata costante per le altezze dei fenomeni che stiamo trattando (mele e poco più). Dato che un corpo arrivato a terra non riesce a cadere più in basso, possiamo considerarlo come livello zero. Tuttavia, se vogliamo  allontanarci di molto dalla Terra, ossia tener conto che g è variabile con l’altezza, le cose cambiano un po’ e lo ZERO è meglio prenderlo molto, molto lontano.

Per adesso, torniamo con i piedi per… terra, dove possiamo dire che l’energia potenziale di un corpo che sta al suolo vale 0, mentre cresce andando ad altezze h.

Facciamo due conti. All’inizio della caduta la mela ha solo energia potenziale e vale U = gmh. Quando arriva in fondo la sua energia è solo cinetica e vale E_C = ½ mv². Se la portassimo in alto, invece, l’energia cinetica sparirebbe quando si ferma, ma acquisterebbe energia potenziale. Durante la caduta decresce il valore dell’energia potenziale (h decresce), mentre sale quello dell’energia cinetica (v cresce). A una certa altezza intermedia un corpo possiede sia energia cinetica che energia potenziale gravitazionale.

Tutte queste parole portano a una conclusione estremamente semplice: la somma dell’energia cinetica e di quella potenziale deve rimanere costante. Abbiamo quasi automaticamente stabilito che l’energia meccanica rimane costante, cambia solo il modo con cui si manifesta.

Liberi per sempre

Ormai sappiamo che una massa nello spazio ha una sua energia potenziale dovuta soltanto alla gravitazione della Terra o di qualsiasi corpo celeste. Attenzione, però: non confondiamo energia potenziale gravitazionale con accelerazione gravitazionale. A mano a mano che ci si allontana dalla Terra l’accelerazione di gravità diminuisce, mentre invece aumenta l’energia potenziale. Essa aumenta sempre di meno, ma aumenta, dato che trasportando un corpo sempre più in alto aumenta l’energia immagazzinata. Senza quasi volerlo ritorniamo alla definizione della velocità di fuga… che avevamo già descritto QUI (addirittura per costruirci un buco nero), ma che preferiamo scrivere di nuovo per non farvi saltellare troppo.

Cosa bisogna fare per abbandonare indefinitamente la Terra e non subirne più la forza gravitazionale? Basta imprimere alla massa una velocità che la trascini nello spazio fino a distanza infinita. Momento per momento, la velocità della massa diretta verso lo spazio diminuisce di intensità (per effetto della gravità), ma ugualmente diminuisce il rallentamento che subisce, dato che diminuisce la forza gravitazionale (e anche l’accelerazione di gravità) che cerca di opporsi al moto. L’energia cinetica diminuisce un po’ alla volta, mentre aumenta un po’ alla volta l’energia potenziale. La massa continua ad allontanarsi indefinitamente fino a raggiungere velocità zero all’infinito. Se l’energia cinetica diventa zero, tutta l’energia è energia potenziale. Essa è la massima possibile.

Ma qual è la massima energia potenziale possibile? Non dobbiamo farci ingannare dagli esperimenti fatti con la mela. In quel caso abbiamo considerato l’accelerazione di gravità costante e abbiamo scelto il livello del suolo come altezza zero, dove considerare nulla l’energia potenziale.

Queste scelte non hanno creato problemi dato che si lavorava sempre con differenze di energie e ad altezze ridicole rispetto al suolo terrestre. La scelta del livello zero per quella potenziale era quindi del tutto arbitraria. In altre parole, abbiamo studiato il moto in un ambito estremamente ristretto, ma più che sensato per qualche mela o qualche pallina.

Adesso, però, vogliamo andare ad altezze estremamente più grandi del raggio terrestre. Non possiamo più considerare l’accelerazione di gravità g come una costante. Dobbiamo tenere conto che essa varia seguendo la legge di gravitazione universale e non con la forza peso che è solo una sua approssimazione nei pressi della superficie terrestre. Per far ciò dobbiamo considerare la massa della Terra concentrata in un punto e pensare che quando un corpo si trova al suolo esso è comunque soggetto alla gravità della massa terrestre che gli sta “sotto”. In altre parole, la sua energia potenziale al suolo non può essere considerata zero come prima, ma ha un valore ben definito che dipende dal raggio della Terra.

L’accelerazione di gravità è:

g = GM/r²

come si vede essa non è assolutamente costante, ma diminuisce velocemente al crescere della distanza r dal centro della Terra di massa M (dove, come già detto, si può immaginare di concentrare tutta la massa).

Quanto vale allora l’energia potenziale al suolo, ossia a una distanza R dal centro della Terra? Facile a scriversi:

U = mgR = m GM/R

Tuttavia, qual è il segno di questa energia? Noi l’avevamo considerata zero e avevamo considerate positive quelle ad altezze maggiori. Nessun problema in quanto g era costante e potevamo scegliere a piacere il livello zero. Ora non possiamo più farlo, dato che sappiamo che g dipende dalla distanza dal centro della Terra.

Il valore minimo dell’energia deve essere quello raggiunto al centro della Terra. E’ lì che la distanza è uguale a zero. Ma se r = 0, l’energia tende a essere infinita, dato che il raggio compare al denominatore. Dividendo per un numero sempre più piccolo, sappiamo benissimo che la grandezza deve tendere a infinito. L’infinito sembra un numero molto grande e non piccolo. Accidenti, come possiamo avere un numero infinito, ma piccolissimo? Banale. Lo otteniamo solo se il suo valore è sempre negativo.

Deve essere allora:

U =  - GmM/r    …. (1)

Non era difficile capirlo fin dall’inizio. Quando si porta un corpo dal centro della Terra fino a un’altezza R (uguale al raggio, ossia fino alla superficie terrestre) il lavoro è negativo, in quanto è contrario al verso della forza di attrazione gravitazionale. Ma se il lavoro è negativo vuol dire che la differenza di energia deve essere negativa.

Possiamo perciò concludere che se la distanza di un corpo di massa m dalla superficie terrestre (o di qualunque altro corpo celeste) è tale da non poter trascurare le variazioni della forza gravitazionale con la distanza, allora l'energia potenziale ad una distanza r dal centro del corpo celeste è definita da una quantità sempre negativa, il cui “valore assoluto” (la parte positiva) decresce all’allontanarsi dal centro, in modo che cresca il valore dell’energia. Una quantità negativa che diventa più piccola aumenta il suo valore.

Qual è il valore massimo dell’energia potenziale? Essendo sempre negativa raggiunge il suo valore massimo quando arriva a zero. Come fa a diventare zero? Basta che la distanza r dal centro della Terra diventi infinita. Più è grande il denominatore della (1) è più piccola, in valore assoluto, è l’energia e quindi più grande il suo valore negativo.

Cosa ne consegue? Che la massa m deve essere lanciata a una velocità tale da raggiungere un valore di energia potenziale massima (uguale a zero) proprio all’infinito. Come arriverà in quel punto la nostra massa? La sua velocità è diventata zero, ossia è diventata zero anche la sua energia cinetica. L’energia meccanica totale della pietra in queste condizioni deve perciò essere uguale a zero (0 + 0 = 0).

Per la conservazione dell’energia deve perciò sempre valere:

E_C + U = 0

Questa relazione deve essere valida anche al momento del lancio. L’energia cinetica deve quindi essere uguale e contraria a quella potenziale posseduta dalla massa e che dipende solo dalla distanza r dal centro della Terra. Solo così si ottengono sia la condizione all’infinito (annullamento dell’energia meccanica totale) che la conservazione dell’energia meccanica totale.

½ mv₀² = GmM/r       ….  (2)

Dalla (2) si ottiene subito la velocità necessaria per allontanarsi indefinitamente dalla gravitazione terrestre e raggiungere velocità zero all’infinito. Se r = R (raggio della Terra), ossia se la massa m viene lanciata dalla superficie terrestre, la velocità viene chiamata velocità di fuga e indicata con v_f. Essa si ricava subito dalla(2), dove tutte le grandezze sono note tranne proprio la velocità.

v_f² = (2GM/R)

e infine:

v_f = (2GM/R)^½  …. (3)

Nel caso della superficie terrestre essa vale 11.2 km/s.

Lo so, lo so, ho ripetuto cose già ben note, ma quando si entra nel mondo della meccanica i concetti diventano ciliegine e uno tira l’altro…  La parte precedente può quindi essere saltata da chi conosce bene la meccanica elementare, ma è pur sempre un richiamo che può essere utile avere sotto mano.

Quanto detto per la Terra vale per qualsiasi altro oggetto celeste: basta cambiare la massa M. La (3) ci dice, però, anche un’altra cosa molto importante (che già dovremmo sapere): la velocità di fuga non dipende dalla massa dell’oggetto. Per mandare nello spazio infinito una pietra o un’astronave mostruosamente grande la velocità necessaria è la stessa (cambia solo la forza necessaria). D’altra parte, anche la velocità di caduta sulla Terra dall’infinito (in assenza di altre masse attrattive) è indipendente dalla massa del corpo, come già Galileo si era sforzato di dimostrare.

Abbiamo capito che a parità di distanza dal ragno centrale, l’energia potenziale gravitazionale ha un certo valore. Se ci allontaniamo cambia in relazione all’altezza. In parole povere esistono superfici (in questo caso più o meno simili a superfici sferiche, in quanto la Terra è quasi una sfera) che hanno la stessa energia potenziale. Ed ecco che abbiamo creato una nuova ragnatela… una ragnatela energetica.

Una nuova ragnatela

E se invece di avere solo la Terra, avessimo due corpi molto massicci? Le curve di energia potenziale costante non sarebbero più sfere, ma superfici più complesse.  In altre parole, arriviamo, finalmente, al caso delle superfici equipotenziali attorno a sistemi stellari doppi e alla definizione di lobi di Roche e di punti lagrangiani in sistemi rotanti.

Dobbiamo, prima, introdurre (abbiate pazienza) alcuni concetti, che non ci sono del tutto nuovi, ma che meritano di essere trattati con maggiore attenzione.

Torniamo alla stella singola e riprendiamo in mano l’energia potenziale. Essa non è altro che il lavoro compiuto da una massa m (la nostra mosca caduta nella ragnatela) per passare da una certa distanza A a una distanza B rispetto alla massa della stella-ragno M (Fig. 16).

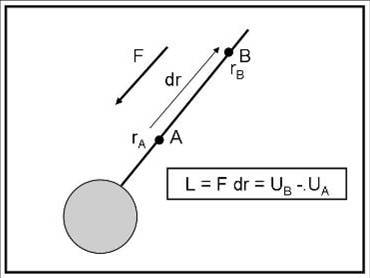
Il lavoro per passare da A a B può essere scritto:

L =  F dr = U_B – U_A = ∫_B^A GmM/r =  GMm (1/r_A – 1/r_B)

Ripetiamoci, dato che non fa mai male: si definisce come energia potenziale di un punto P, a distanza r dal centro della stella (il suo baricentro), la grandezza:

Ur = - GmM/r

Il segno meno sta a indicare che questa energia è sempre negativa (il lavoro per andare verso lo spazio è negativo, dato che ci si muove in verso opposto alla forza di gravità).

L’energia potenziale gravitazionale raggiunge il suo valore massimo, ossia zero, proprio all’infinito. Solo in quel punto ipotetico è massima l’energia immagazzinata. Ripeto ancora: non confondiamola con l’accelerazione di gravità che tende a zero in quanto raggiunge il suo valore minimo. L’equazione è quella di un ramo di iperbole e quindi può essere facilmente tracciata nella Fig. 17.

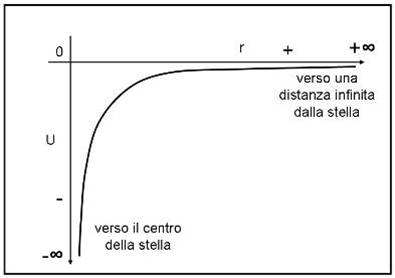
Ricordiamoci bene, ancora una volta, questi concetti: l’energia potenziale in un campo gravitazionale è sempre negativa e cresce al crescere della distanza dal baricentro della massa della stella. Mentre l’accelerazione gravitazionale diventa sempre meno intensa, l’energia potenziale aumenta. D’altra parte è ovvio: per arrivare a una distanza infinita si deve fare più lavoro che per giungere a poche migliaia di chilometri!

La formula:

U = - GMm/r

ci regala una grandezza importantissima, ma, ancora una volta, contiene la massa m dell’astronave o del corpo che abbiamo usato per definirla nell’intorno della stella. Agiamo come fatto per il campo gravitazionale e dividiamo entrambi i membri per la massa m. Otteniamo:

Q = U/m = - GM/r

Questa grandezza prende il nome di potenziale ed è indipendente dalla massa dell’oggetto caduto nella rete. Essa dipende solo dalla massa della stella-ragno e dalla distanza rispetto al suo baricentro.

Fissiamoci bene in testa la differenza tra energia potenziale e potenziale. La prima è il lavoro che si deve fornire alla massa m per portarla fino all’infinito, la seconda è invece il lavoro che è necessario fornire alla massa m unitaria per portarla fuori dal campo (cioè a distanza infinita). La differenza è enorme anche se non sembra! Nel primo caso in un certo punto P dello spazio potremmo avere tanti valori di energia, dato che dipende dalla massa; nel secondo caso vi è invece un valore unico, indipendente dalla massa del corpo che va a occuparlo.

Nel campo gravitazionale (anch’esso indipendente dalla massa) è allora possibile disegnare delle curve molto speciali che rappresentano il luogo dei punti aventi lo stesso potenziale, ossia le curve equipotenziali. La nostra mappa si arricchisce.

Nel caso di una stella singola il campo gravitazionale è definito dalle linee di forza che convergono verso il centro. Le curve equipotenziali devono allora essere delle circonferenze che si allargano sempre più andando verso l’esterno. Il potenziale, infatti, dipende solo dalla distanza dal centro della stella (la massa è sempre la stessa).

E’ ovvio che le curve equipotenziali sono proprio quelle in cui la distanza dal centro della stella è costante. La curva che ha queste caratteristiche è proprio la circonferenza che ha per centro il baricentro della stella. Ne consegue anche che la tangente in un punto P della circonferenza (linea equipotenziale) è sempre perpendicolare alla retta passante per il centro e per quel punto. In altre parole la tangente punto per punto di una linea equipotenziale è perpendicolare alle linee di forza che definiscono il campo gravitazionale. La Fig.18 spiega la situazione molto meglio di tante parole.

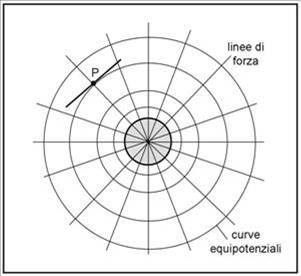
Ovviamente, noi abbiamo parlato di linee equipotenziali, perché disegniamo tutto su un piano. In realtà esse sono superfici sferiche di raggio crescente. Anche il campo gravitazionale si estende a tutto lo spazio a tre dimensioni attorno alla stella. La Fig. 18 è quindi una sezione piana di una mappa a tre dimensioni.

Raddoppiamo la nuova ragnatela

Vediamo come si trasformano le curve equipotenziali in un sistema doppio di stelle? Non è difficile immaginarselo, dato che esse devono sempre essere perpendicolari alle linee di forza. E le linee di forza di un sistema doppio le avevamo già viste nel campo gravitazionale.

La Fig. 19 schematizza molto qualitativamente la situazione.

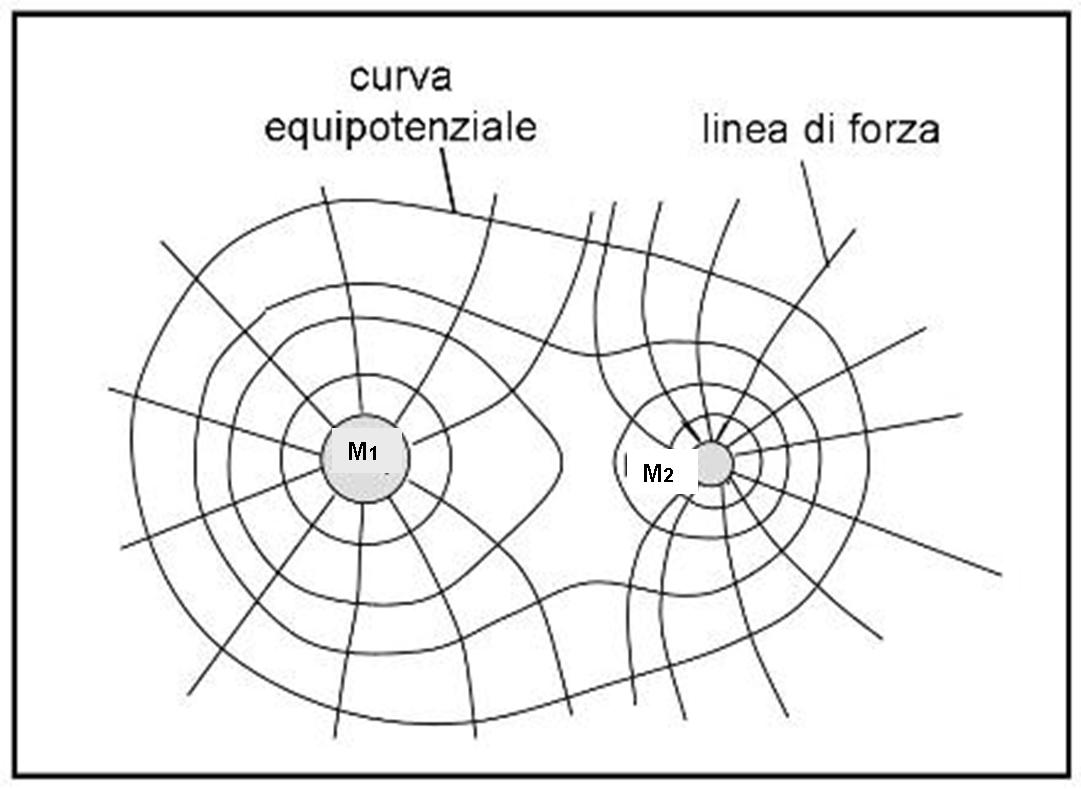
E’ proprio attraverso lo studio delle superfici equipotenziali che si possono stabilire i limiti di crescita delle singole stelle, il momento in cui inizia il trasferimento di massa e molte altre cose. Cerchiamo di descrivere la situazione limitandoci, ovviamente, ai concetti essenziali e tralasciando le formule più complicate.

Il potenziale totale

Consideriamo un sistema formato da due stelle che rivolvano entrambe attorno al proprio baricentro, come quello rappresentato in Fig. 20.

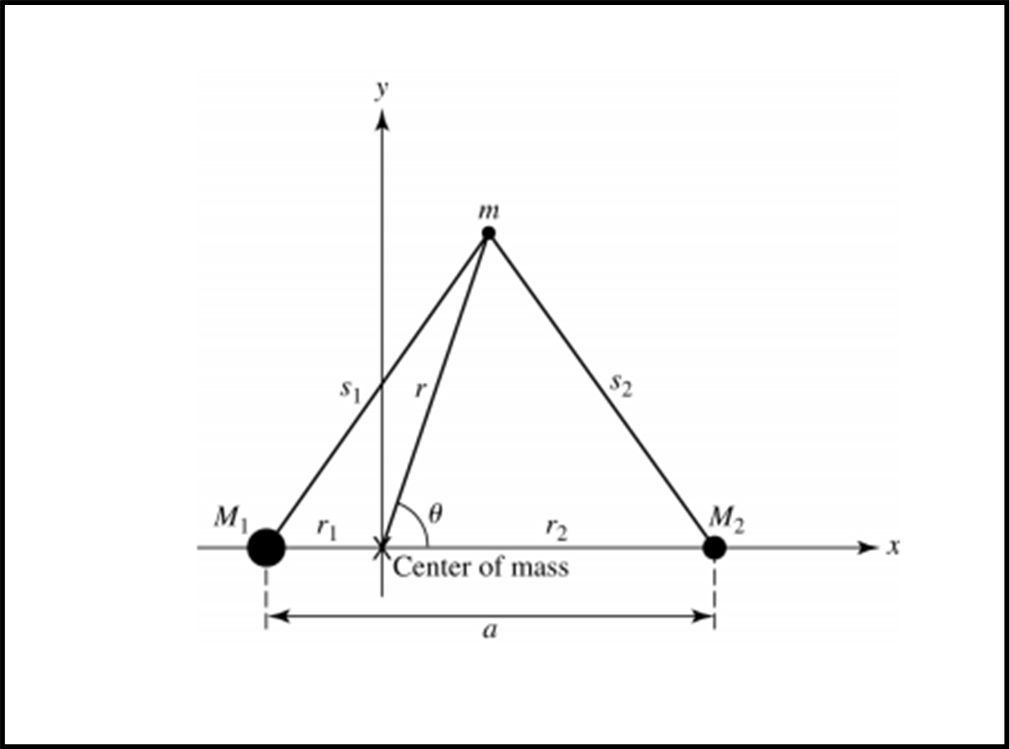
Il potenziale di un punto immerso nel campo gravitazionale del sistema è dato, come ormai sappiamo, dalla somma dei potenziali delle singole stelle

Q = - GM₁/s₁ - GM₂/s₂

A questo punto, immaginiamo di entrare nel sistema rotante e di mantenere fisso l’asse che congiunge le stelle (cosa che abbiamo già fatto spesso), prendendo come origine il baricentro del sistema (ma non è obbligatorio, l’importante è che si sia solidale con la rotazione).

Le condizioni di equilibrio di un punto devono, allora, anche tener conto della forza centrifuga. Al potenziale gravitazionale bisogna allora aggiungere anche il potenziale della forza centrifuga.

La forza centrifuga agente sulla massa m è data da:

F_C = m ω²r

Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana (chissà... un giorno), ma possiamo lavorare in termini di energia potenziale, sapendo che la forza (in questo caso centrifuga) può essere espressa come:

F_C = - dU_C/dr         (la variazione dell’energia è proprio la forza moltiplicata per la variazione di r)

La differenza di energia potenziale, ossia il lavoro, relativa a questa forza è data da:

ΔUc = - ∫₀^r m ω²r dr = - [1/2 m ω²r²]₀^r =  - 1/2m ω²r² + 0

Avendo posto l’energia uguale a zero per r uguale a zero.

Dividiamo per m e otteniamo il potenziale centrifugo:

Qc =  -1/2 ω²r²

In conclusione, il potenziale totale risulta:

Φ = - GM₁/s₁ - GM₂/s₂ - 1/2 ω²r²

L’intersezione delle superfici di uguale potenziale con il piano orbitale è dato dalla Fig. 21, che conosciamo molto bene. In essa sono anche segnati i punti lagrangiani, che sono i punti in cui  la forza gravitazionale è esattamente uguale alla forza centripeta necessaria a farli ruotare con la velocità angolare ω, ossia a restare fissi nel sistema rotante. Ma ci torneremo ancora sopra, alla fine.

L’analisi della Fig. 20 porta alle seguenti relazioni (ricordando il teorema di Carnot):

s₁² = r₁² + r² + 2r₁r cos(ϑ)

s₂² = r₂² + r² - 2r₂r cos(ϑ)

mentre la legge di Newton permette di scrivere:

ω² = (2π/P)² = G (M₁ + M₂)/a³

Le ultime quattro relazioni permettono, fatti i dovuti passaggi, di calcolare il potenziale totale in ogni punto del piano orbitale delle due stelle di massa M₁ e M₂.

Come esempio più che significativo, consideriamo soltanto la componente della forza che agisce sulla nostra particella di massa m lungo l’asse x. La forza non è altro che la derivata del potenziale rispetto a uno spostamento dx, per cui è sufficiente trovare gli zeri di dΦ/dx. Normalizzando adeguatamente la funzione Φ, in relazione alle masse in gioco e alla loro distanza, si ottiene il grafico di Fig. 22.

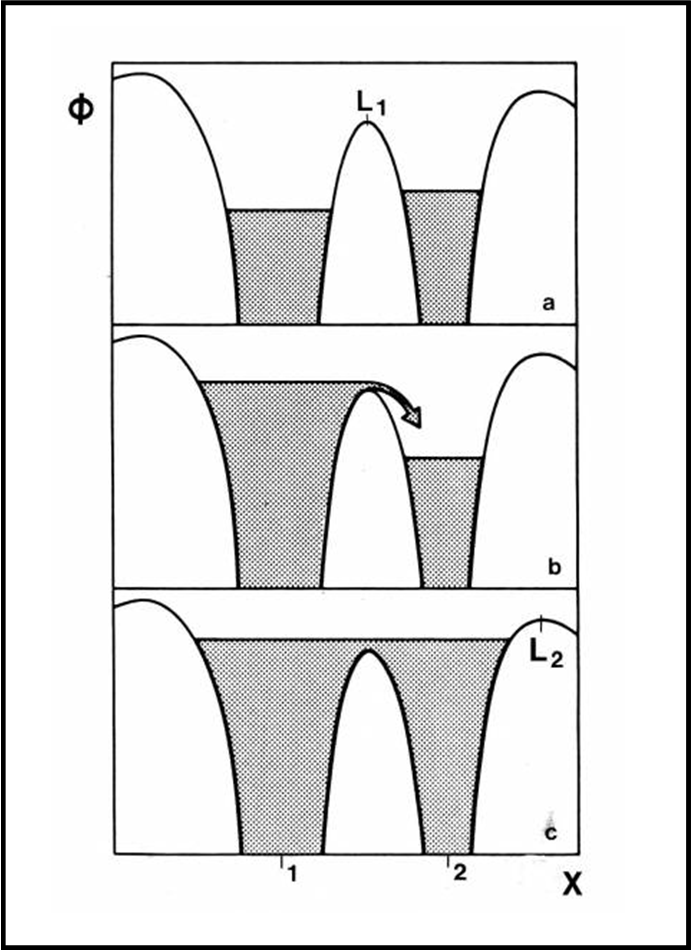
I massimi della funzione sono i punti lagrangiani L1, L2 e L3, proprio quelli dove la tangente alla curva potenziale è orizzontale (derivata nulla: le derivate sono spiegate nell’articolo 23 e seguenti delle lezioni di matematica). In corrispondenza delle due stelle abbiamo invece i punti di minimo potenziale. I punti in cui si annulla la derivata sono i punti in cui si annulla la forza agente su di loro e quindi punti fermi nel sistema rotante con le due stelle. Possiamo proprio chiamarli buchi di potenziale.

Le stelle doppie strette: Ragni e prede nello stesso tempo

La Fig. 22 vale per qualsiasi particella, anche per quelle che appartengono alle due stelle “fisiche”, che nella trattazione precedente abbiamo considerato puntiformi. In altre parole le stelle reali si sistemano all’interno dei due minimi di potenziale, riempiendo un po’ alla volta tutto “il buco” compreso tra i vari massimi. Immaginiamo quindi, di vedere il profilo di Fig. 22, come una serie di colline in cui continua a cadere pioggia che riempie sempre di più i buchi. Ovviamente, la “pioggia” è la materia stessa delle due stelle. La materia stellare aumenta il proprio volume (non la massa, per adesso) fino a colmare il buco più basso (relativo alla collina L1) e può passare da uno all’altro dei buchi stellari originali. Attraverso quel solo punto, L1, le stelle possono svolgere i loro giochi di travaso di materia.

L2 e L3 vengono usati quando entrambe le stelle (diventate praticamente una sola utilizzando il punto L1) arrivano al limite delle colline esterne. La materia può uscire nello spazio circostante (binarie a inviluppo unico).

Ovviamente, è ormai chiaro a tutti che i buchi di potenziale rappresentano i lobi di Roche.

Ricapitolando: Una stella, durante la sua evoluzione, aumenta il diametro fino a riempire completamente il suo lobo di Roche. La materia stellare deve trovare una via d’uscita e questa è proprio offerta da L₁. Basta una piccola spintarella data dal vento stellare e la materia oltrepassa quel punto di equilibrio instabile e inizia a cadere verso la compagna. L₂ e L₃ ci dicono, invece, che quando le stelle riempiono entrambi i lobi di Roche, la materia può sfuggire verso l’esterno, attraverso di loro.

Torniamo alla Fig. 21, con maggiore conoscenza della situazione e ripetiamo ancora una volta certi concetti in modo leggermente diverso, ma altrettanto esplicativo. Se siete arrivati alla “noia”, benissimo! Vuol dire che avete capito perfettamente una configurazione fondamentale per l’evoluzione stellare delle stelle doppie strette (ricordiamo che sono proprio loro che portano alle supernove di tipo Ia).

Le linee equipotenziali ci dicono, in generale, che se stiamo vicini alle stelle, il campo che domina è quello gravitazionale, mentre se si va verso l’esterno prende il sopravvento quello centrifugo.  Nei dintorni delle due masse stellari le superfici dipendono solo dalla massa più vicina e sono molto simili a circonferenze (leggermente deformate per effetto della seconda massa). A un certa distanza dalle stelle, la superficie equipotenziale diventa una specie di otto. Il punto L₁ è quindi estremamente “imbarazzato”. Si trova proprio in mezzo ai due giganti. Un oggetto posto in quella posizione rimane in equilibrio, ossia rimane immobile rispetto alle due stelle che nel sistema rotante sono fisse per definizione (QUI abbiamo descritto cosa vede un satellite artificiale in orbita in L1). In altre parole, ruota solidalmente con loro. Non confondiamo il punto lagrangiano L₁ con il baricentro! Sono due cose completamente diverse.

In parole veramente povere, potremmo dire che in quella posizione l’attrazione gravitazionale di M₂ cancella parzialmente quella di M₁. Tuttavia, per i più smaliziati questa considerazione può non bastare. Infatti, qualcuno potrebbe dire: “Se M₂ sta ferma, come può stare fermo un punto che è più vicino di lei a M₁? Il suo periodo di rotazione attorno a M₁ dovrebbe essere più breve. In altre parole, il punto dovrebbe muoversi rispetto al sistema che mantiene fissa la direzione M1- M2.”

Ciò sarebbe vero se non ci fosse M₂. Questa, nel suo piccolo, sottrae un po’ di forza centripeta all’oggetto “imbarazzato” e gli rallenta il periodo di rivoluzione facendolo diventare uguale al suo. E quindi NON lo fa ruotare nel sistema rotante della figura.

Gli altri punti di equilibrio sono meno intuitivi. L₂ si trova dalla parte opposta di M₂ rispetto a L₁. Ciò che capita in quel punto è che la forza centrifuga eguaglia perfettamente quella gravitazionale dovuta a M₁ e M₂. Anch’esso allora ruota solidalmente con il sistema rotante, ossia rimane fermo rispetto alle due masse. L₃ è l’analogo di L₂, dalla parte opposta del sistema.

I punti L₄ e L₅ sono, invece,  più interessanti da un punto di vista dinamico. Essi si trovano nel terzo vertice dei due triangoli equilateri che hanno come altri due vertici le masse M₁ e M₂. Il loro equlibrio è già stato trattato ampiamente.

Ribadiamo il concetto in modo sintetico: avendo distanza uguale rispetto alle due masse, essi subiscono attrazioni gravitazionali che dipendono soltanto dalle masse delle due stelle. In altre parole, il rapporto tra le forze gravitazionali che subiscono è uguale al rapporto delle masse. Queste condizioni fanno sì che la risultante delle due forze passi esattamente per il baricentro del sistema rotante. Di conseguenza non causa alcuna rotazione supplementare ed essi rimangono fissi nel sistema solidale con le due masse.

 

QUI una trattazione della Lagrangiana e dell'equazione di Eulero-Lagrange