Categorie: Matematica
Tags: derivate successive serie di Taylor teorema di Lagrange
Scritto da: Vincenzo Zappalà
Commenti:16
38. Costruzione “rigorosa” della formula di Taylor (seconda parte) ***/****
Concludiamo la costruzione della serie di Taylor, introducendo il suo termine generale. L'ho letta e riletta, ma non garantisco che non vi sia ancora qualche refuso. Picchiate duro e non abbiate pietà di me!!
Definiamo:
f ”(x2) = f "(x0) + φ
La (7) diventa:
f(x) = f(x0) + (x – x0) f ’(x0) + f ”(x2)(x – x0)2/2 = f(x0) + (x – x0) f ’(x0) + (f ”(x0) + φ)(x – x0)2/2
f(x) = f(x0) + (x – x0) f ’(x0) + f”(x0)(x – x0)2/2 + φ(x – x0)2/2 …. (9)
Derivando due volte
f ’(x) = f ’(x0) + f ”(x0)(x – x0) + φ(x – x0)
f ”(x) = f ”(x0) + φ
segue ancora una volta che φ deve essere uguale a zero per x = x0
Abbiamo ripetuto questa parte, ma si poteva concludere subito che:
φ = C3(x - x0)
Andiamo a sostituire nella (9) e si ha:
f(x) = f(x0) + (x – x0) f ’(x0) + f ”(x0) (x – x0)2/2 + C3(x - x0)(x – x0)2/2
f(x) = f(x0) + (x – x0) f ’(x0) + f ”(x0) (x – x0)2/2 + C3(x – x0)3/2 …. (10)
Deriviamo due volte per trovare il valore di C3
f ’(x) = f ’(x0) + f ”(x0) (x – x0) + 3C3(x – x0)2/2
f ”(x) = f ”(x0) + 3C3(x - x0)
E applicando ancora il teorema di Lagrange
3C3 = (f ”(x) – f ”(x0))/(x – x0) = f III(x3)
Con x0 < x3 < x
Da cui C3 = f III(x3)/3
E, infine, sostituendo nella (10)
f(x) = f(x0) + (x – x0) f ’(x0) + f ”(x0) (x – x0)2/2 + f III(x3) (x – x0)3/6 …. (11)
Questa è una serie che approssima ancora meglio la funzione di partenza nell’intorno del punto x0, tenendo conto anche del termine di secondo grado (ossia rappresenta la parabola osculatrice). L’errore che si commette è sempre dato da:
R3 = f III(x3)(x – x0)3/6
Che ovviamente tende a zero più velocemente di R2, contenendo il termine al cubo.
Non fatemi proseguire più di tanto… Basta ripetere lo stesso procedimento un’altra volta e si ottiene (provare per credere):
f(x) = f(x0) + (x – x0) f ’(x0) + f ”(x0)(x – x0)2/2 + f III(x0)(x – x0)3/6 + f IV(x4)(x – x0)4/24
Che rappresenta la cosiddetta cubica osculatrice… e via dicendo!
Continuando ad applicare Lagrange e inserendo sempre nuove costanti si otterrà, alla fine:
f(x) = f(x0) + (x – x0) f ’(x0) + f ”(x0) (x – x0)2/2 + f III(x0)(x – x0)3/6 + f IV(x0)(x – x0)4/24 + …. + f n(x0) (x – x0)n /n! + Rn+1 …. (12)
Con
Rn+1 = f n+1(xn+1)(x – x0)n+1 /(n + 1)!
Riassumendo: lo sviluppo in serie di una funzione f(x) continua e derivabile indefinitamente in un certo intervallo, può essere approssimata attraverso una serie di potenze di x fino al grado n desiderato. n è anche l’ordine di derivazione raggiunto. L’errore che si commette è rappresentato dal termine di grado superiore che contiene la derivata di ordine superiore, calcolata in un punto dell’intervallo (x, x0) che soddisfa il teorema di Lagrange.
Per non portarci dietro un sacco di termini, conviene scrivere la serie di Taylor utilizzando il simbolo di sommatoria (Σ ) che riunisce tutti termini in uno solo ricorrente. In parole matematiche:
f(x) = Σ∞n = 0 f n(x0)(x - x0)n/n! …. (13)
Che si legge proprio come la somma da n uguale zero a n = infinito del prodotto tra la derivata ennesima calcolata nel punto in cui si vuole approssimare la funzione, moltiplicata per la potenza ennesima di (x – x0) e divisa per il fattoriale di n. La funzione in x0 è stata approssimata da un polinomio con termini di grado crescente, ossia da curve che si avvicinano sempre di più a quella di partenza.
Ovviamente andando fino a infinito non esiste resto. Tuttavia, nessuno può andare a infinito per cui n si ferma a un certo valore e ne deriva un resto dato dalla solita formula di grado subito superiore a n.
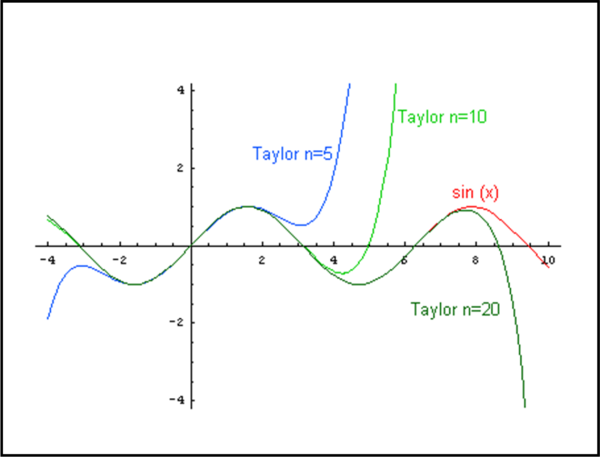
A titolo di esempio, ma ci torneremo sopra, potete vedere nella Fig. 3 come la funzione sen(x) venga approssimata dalla serie di Taylor, fermata a vari valori di n, nel punto x0 = 0 (e, quindi, diventata di Maclaurin). Niente male…
Vi sono anche altri metodi per ricavare la formula di Taylor, più o meno empirici e/o intuitivi. Non vorrei esagerare e mi limiterei a quelli presentati negli ultimi articoli. Uno è veramente semplificato, l’altro segue una regola precisa e si basa su un teorema. A voi la scelta… l’importante è ricordare la formula di Taylor e la sua sorellina semplificata di Maclaurin.
La prossima volta cercheremo di applicarla per evidenziare ancora meglio la sua importanza matematica e non solo.
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica
16 commenti
posto qui anche se andrebbe nella prima parte;
volevo solo aggiungere un cosa
sulla scelta del valore della funzione ε che sembra arbitrario, ε=C(x-x0)
in realtà potrebbero esserci altri polinomi o funzioni
che soddisfano la condizione ε(x0)=0
se parto da:
f'(x1)=f'(x0)+ ε(x)=f(x)-f(x0)/(x-x0)
f(x)=f'(x0) +(x-x0)f'(x0)+ (x-x0)ε(x)
se lascio l'espressione ε(x) ed eseguo i calcoli
con le regole della derivata del prodotto ottengo:
f'(x)=f'(x0) +ε(x) +(x-x0)ε'(x)
f'(x0)=f'(x0) + ε(x0); implica ε(x0)=0
f'(x)-f(x0)/(x-x0)=ε(x)/(x-x0) + ε'(x)=f''(x2)=costante
ma allora necessariamente ε(x) deve essere un polinomio di grado 1
e valere zero in x0, quindi deve essere del tipo C2(x-x0)
non so se era necessario..
ottimo Umberto. Il ragionamento non fa una piega...
Ricordo il titolo (ma solo il titolo) del capitolo sul libro di analisi: "La formula di Taylor e il resto di Peano". Si tratta genericamente del resto di cui parli tu, o di un particolare caso per qualche valore n che abbia un significato particolare?
Caro Enzo, innanzitutto volevo complimentarmi con Umberto, che ha esposto un interessante ragionamento....
il bello è che pur usando metodi o ragionamenti leggermente diversi si arriva alla medesima conclusione.
Sono rimasto molto incuriosito dalla figura 3.... inizialmente non riuscivo a capire come tracciare le curve delle funzioni di approssimazioni (Taylor n=5; n=10; n=20), poi ragionandoci....
Il ragionamento si basa su due proprietà di seno e coseno:
Il seno assume valore 0, quando l'angolo è uguale a 0°; 180°; 360° e multipli;
Il coseno assume valore 1, quando l'angolo è uguale a 0°; 180°; 360° e multipli;
La derivata di sin(x) = cos (x) e la derivata di cos (x) = -sin (x):
La derivata di -sin(x) = -cos (x) e la derivata di -cos (x) = sin (x):
Nella figura ho solo indicato sull'asse x i radianti invece degli angoli:
http://www.astrobin.com/full/187783/P/
Dato che la funzione sin (x) passa per l'origine degli assi, questa si può usare come punto x0 per approssimare la funzione per cui è possibile usare la serie di Maclaurin (Taylor applicata all'origine degli assi).
f (x) = f (0) + f’(0) x/1! + f ”(0) x²/2! + f III(0) x³/3! + …. f n (0) xn/n!
f (x) = f sin(0) + f’ sin(0) x/1! + f ”sin(0) x²/2! + f III sin(0) x³/3! + …f ^n sin(0)x^n/n!
Ora basta applicare le due proprietà di seno e coseno e calcolare le loro derivate successive:
f sin (0) = 0 =0
f' sin (0) = cos (0) =+1
f'' sin (0) = -sin (0) = 0
fIII sin (0) = -cos (0) = -1
fIV sin (0) = sin (0) = 0
fV sin (0) = cos (0) = +1
fVI sin (0) = -sin (0) = 0
fVII sin (0) = -cos (0) = -1
fVIII sin (0) = sin (0) = 0
fIX sin (0) = cos (0) = +1
fX sin (0) = -sin (0) = 0
A questo punto sostituisco le derivate appena trovate nella serie di Maclaurin
f (x) = sin(0) + cos(0) x/1! - sin(0) x²/2! - cos(0) x³/3! + sin(0) x^4/4! + cos(0) x^5/5! -sin(0) x^6/6! - cos (0) x^7/7! + sin(0) x^8/8! + cos(0) x^9/9! - sin(0) x^10/10!
Sostituisco a seno e coseno i valori calcolati a 0° o 0 radianti che siano:
f (x) = 0 + (1) x/1! - (0) x²/2! - (1) x³/3! + (0) x^4/4! + (1) x^5/5! -(0) x^6/6! - (1) x^7/7! + (0) x^8/8! + (1) x^9/9! - (0) x^10/10!
f (x) = x/1! - x³/3! +x^5/5! - x^7/7! + x^9/9!
Infine, sostituendo ai fattoriali il valore numerico si ottiene:
f (x) = x - x³/6 + x^5/120 - x^7/5040 +x^9/362880
Non so se è corretto questo ragionamento
, ma ho provato ad applicare il risultato usando diversi valori di x e coincide con le curve Taylor n=5 e n=10.
Dalla figura 3 risulta evidente che aumentando il numero che compone la serie, ossia il grado di approssimazione, la curva ottenuta è più fedele a quella originale, anche a maggiori distanza dall'origine degli assi.
La domanda che mi facevo è vuoi vedere che la serie di Taylor può aiutare a determinare il valore di π, la cui approssimazione dipende solo dal grado n della serie ?
Paolo
caro Paolo... hai già risolto gli esercizi che sto per dare... Fermati un attimo
caro Massimo, sì... è un altro modo per esprimere il resto, ossia la parte che "manca" alla soluzione esatta. Ma, per i nostri scopi, direi che possiamo trascurarlo... Mi preme partire con gli integrali al più presto
Grazie Paolo, ho solo cercato di partecipare attivamente a questo argomento (come fai bene tu sempre), anche perché è stato oggetto di troppe controversie...
caro Paolo,
ho dimenticato di rispondere a una parte interessante che hai proposto... Uno dei tanti metodi per approssimare pi greco si basa proprio sullo sviluppo in serie di Taylor di funzioni trigonometriche. Ponendo poi come x0 certi valori si ottiene al primo membro una funzione di pigreco e al secondo un polinomio convergente, Da cui un valore di pigreco. Sono tutte funzioni abbastanza complesse che tengono in conto l'arcoseno e l'arcoseno. Preferirei evitarle... Spesso non convergono molto bene e si utilizzano maggiormente successioni per poi passare al limite... (come fatto a suo tempo per e^x). Magari ne diremo qualcosa, ma preferisco trattare il pigreco attraverso le aree che introducano, nel contempo, - e meglio- il concetto di integrale.
ma si può usare anche l'arcotangente di x e poi porre x = 1, da cui arctan(1) = pigreco/4 e infine pigreco come sviluppo in serie dell'arcotangente. Chi vuol provare può farlo, ma "di nascosto"... (necessita già la conoscenza dell'integrale...). Se no il nostro Diego ci... picchia duro
ovviamente ricordando che la derivata di arctan(x) vale 1/(1 + x^2)... si può fare abbastanza bene... Boccaccia mia statti zitta!!!!
E un caro saluto a Leibniz... 
Buona domenica!!!!!
caro Umberto,
le polemiche suscitate si basavano su un errore di interpretazione del lavoro divulgativo che cerco di svolgere.
Da un lato io non faccio altro che cercare di spiegare (nel modo più semplice possibile) i concetti matematici fondamentali. Essi ovviamente DEVONO fare uso di formule matematiche, per definizione... A volte possono essere un po' pesanti, ma rimangono sempre a livello elementare. Se, per qualcuno o per molti, sono troppo complesse e non istigano ad avvicinarsi, bensì ad allontanarsi da questo argomento, non c'è nessun problema! Non tutto deve essere letto da tutti. Io, però ci provo, dato che -ripeto ancora- la matematica è il linguaggio della fisica ed è difficile interagire con qualcuno parlando solo a segni e non con parole.
Sono d'accordo nel non esagerare, facendo diventare la matematica un circolo chiuso per pochi... e mi sembra di averlo fatto. Chi ha avuto tempo e voglia è passato tranquillamente attraverso i limiti, le derivate e -in modo che definirei quasi infantile- tra poco entrerà nel mondo degli integrali. Le serie possono sembrare un po' esagerate, ma se ci pensate bene non sono altro che l'applicazione delle derivate, niente di più e un buon trampolino per iniziare a sommare tanti termini che tendono a infinito... Non per niente, all'inizio degli integrali mi rifarò nuovamente e nientemeno che ad Archimede e ai suoi metodi matematici. Non possiamo certo considerare la matematica di Archimede un trattazione per pochi intellettuali che si ergono sopra tutti gli altri...
Massima semplicità, quindi, per chi vuole imparare la matematica. Problemi per chi rifiuta anche il quadrato di un binomio? Assolutamente no, dato che penso che nel nostro "circolo" ci sia materiale per tutti e per tutti i gusti.
Ne consegue che sono sempre benvenuti i dubbi e le riflessioni di chi segue la matematica trattata negli articoli. Essi fanno parte integrante dell'argomento e non posso fare altro che rispondere. Le cose prenderebbero una cattiva piega se i commenti tentassero di spostarsi su complicazioni superiori che ho preferito escludere al nostro livello. In questi casi è giusto rimandare ad altri link o risolvere le questioni per via personale. Così ho fatto per pigreco: quando ne parlerò per Archimede OK, quando invece si cerca di andare a formule più complesse, escludo l'utilizzo della sezione commenti... L'arctan, le sua derivate e la serie corrispondente non trova posto nei commenti, anche se posso invitare, chi ne ha la volontà, a provarci!
Mi sembra una strategia corretta, che tenga conto dei vari livelli di interesse. Dovrebbe soddisfare anche il nostro caro Diego che si preoccupava di una deriva verso complicazioni molto elitarie...
. Ho detto deriva...non derivata!!! 
Che ne dite?
Caro Enzo io condivido completamente il modo di procedere che hai esposto.
La risposta alla mia supposizione sull'approssimazione del pi greco è più che sufficiente, entrare nel merito ci svierebbe dal cammino intrapreso verso gli integrali... (tra l'altro la mia trigonometria è debole per affrontare funzioni con arcotangenti... ).
Ciò che a me sembra emergere dal ragionamento sviluppato sulla figura 3, sono le “potenzialità” insite in alcune funzioni particolari, per il comportamento delle loro derivate, mi riferisco funzioni come seno, coseno, o il famoso ex la cui derivata è ex.
Paolo
ho provato ad esprimere la formula di Taylor di arctg(x) nel punto x0=0, passando poi al valore in x=1 della 13) (serie di Taylor), ma non vedo il bisogno di integrali, si intendeva la somma della serie?
(non so se sono andato fuori direttiva)
caro Umberto,
hai perfettamente ragione. Lavorando con arctan si può farne a meno, ma si potrebbero anche usare gli integrali per passare alla primitiva direttamente. I metodi per pigreco sono numerosissimi...
Perfetto Paolo, hai capito lo spirito...
a volte mi sfugge il senso dei tuoi commenti... sei d'accordo oppure no? Io cerco di accontentare tutti... ma una maggiore chiarezza anche da parte tua non sarebbe male... Tu la chiedi, ma poi non la usi
OK... avanti così, allora e tra poco gli integrali e Archimede...