Non bastava l'accelerazione a complicare la vita! Adesso arriva anche il jerk e si tira dietro tutti i suoi parenti.
E va bene, via, riprendiamo il discorso e vediamo che altro ci aspetta!
Concludiamo la costruzione della serie di Taylor, introducendo il suo termine generale. L'ho letta e riletta, ma non garantisco che non vi sia ancora qualche refuso. Picchiate duro e non abbiate pietà di me!!
Questo non è un articolo facile, non tanto per i concetti che esprime, ma piuttosto per il numero di passaggi che siamo obbligati a fare. Si basa su un teorema classico delle funzioni e presenta perciò un metodo rigoroso, che abbisogna, però, di iterazioni successive (mai facili da digerire e da tenere sottocchio). Mi sembrava, però, doveroso proporlo.
Il gioco è quasi terminato e possiamo tornare, lentamente, verso una visione più seria e precisa. Ciò che abbiamo ottenuto, divertendoci, non è altro che una formula di importanza fondamentale.
L’approccio che cerchiamo di usare, per introdurre lo sviluppo in serie di funzioni, vuole arrivare ad approssimare una data funzione attraverso un semplice polinomio di grado n. E’ un approccio, però, che non troverete nei libri, ma che reputo oltremodo intuitivo e utile per arrivare al nocciolo del problema ed essere poi pronti a una trattazione ben più rigorosa e generale. Nel contempo, le derivate successive incominciano ad assumere un ruolo di primo piano. Divertiamoci un po’ a fare un tentativo che appare campato in aria solo a prima vista…
Anche se abbiamo concluso (almeno momentaneamente) lo studio delle funzioni, queste ultime rimangono un punto fondamentale della matematica e continuano a essere nel nostro mirino. Vogliamo arrivare al calcolo dei loro integrali e quindi cominciamo con il loro sviluppo in serie, un argomento poco divulgato che è però di importanza fondamentale.
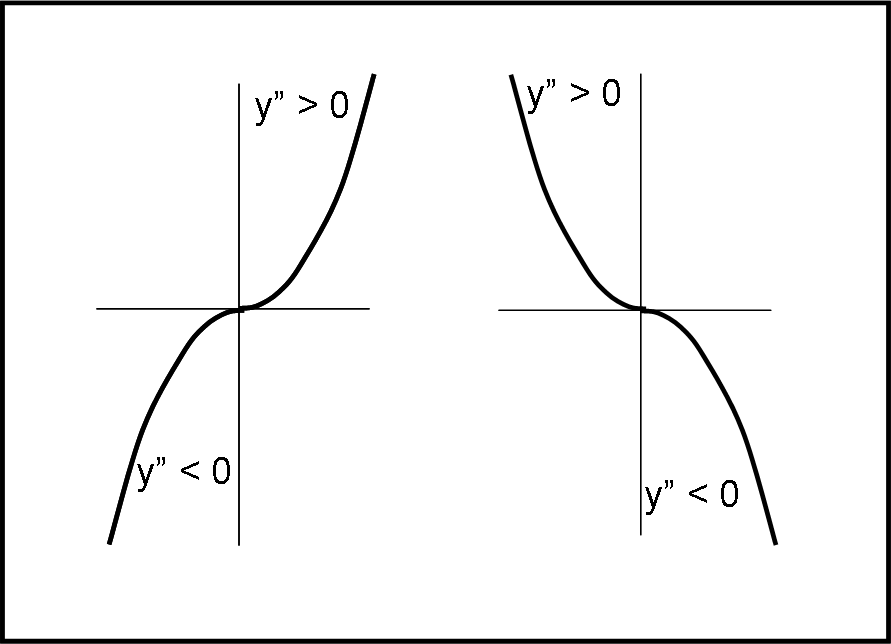
Dopo aver introdotto i massimi, i minimi e i flessi orizzontali in modo molto preliminare, è giunta l’ora di affrontarli più accuratamente attraverso le derivate successive di una funzione. Ci arriveremo lentamente in modo da comprenderne appieno il significato sia matematico che geometrico.