Categorie: Matematica
Tags: derivate successive serie di Taylor teorema di Lagrange teorema di Rolle
Scritto da: Vincenzo Zappalà
Commenti:16
37. Costruzione “rigorosa” della formula di Taylor (prima parte) ***/****
Questo non è un articolo facile, non tanto per i concetti che esprime, ma piuttosto per il numero di passaggi che siamo obbligati a fare. Si basa su un teorema classico delle funzioni e presenta perciò un metodo rigoroso, che abbisogna, però, di iterazioni successive (mai facili da digerire e da tenere sottocchio). Mi sembrava, però, doveroso proporlo.
Prima di partire, dobbiamo ricordare un teorema fondamentale dell’analisi matematica: il teorema di Rolle. Esso sembra del tutto ovvio e, come sempre capita in queste situazioni, la dimostrazione rigorosa è tutt’altro che banale e possiamo tranquillamente evitarla.
Esso può essere enunciato come segue:
Se una funzione f(x) è continua nell’intervallo (a,b), è derivabile e vale inoltre f(a) = f(b), allora esiste sicuramente una x0 nell’intervallo (a,b) in cui f ’(x0 ) = 0.
Abbiamo scritto qualcosa di veramente semplice e intuitivo, che viene descritto perfettamente nella Fig. 1.
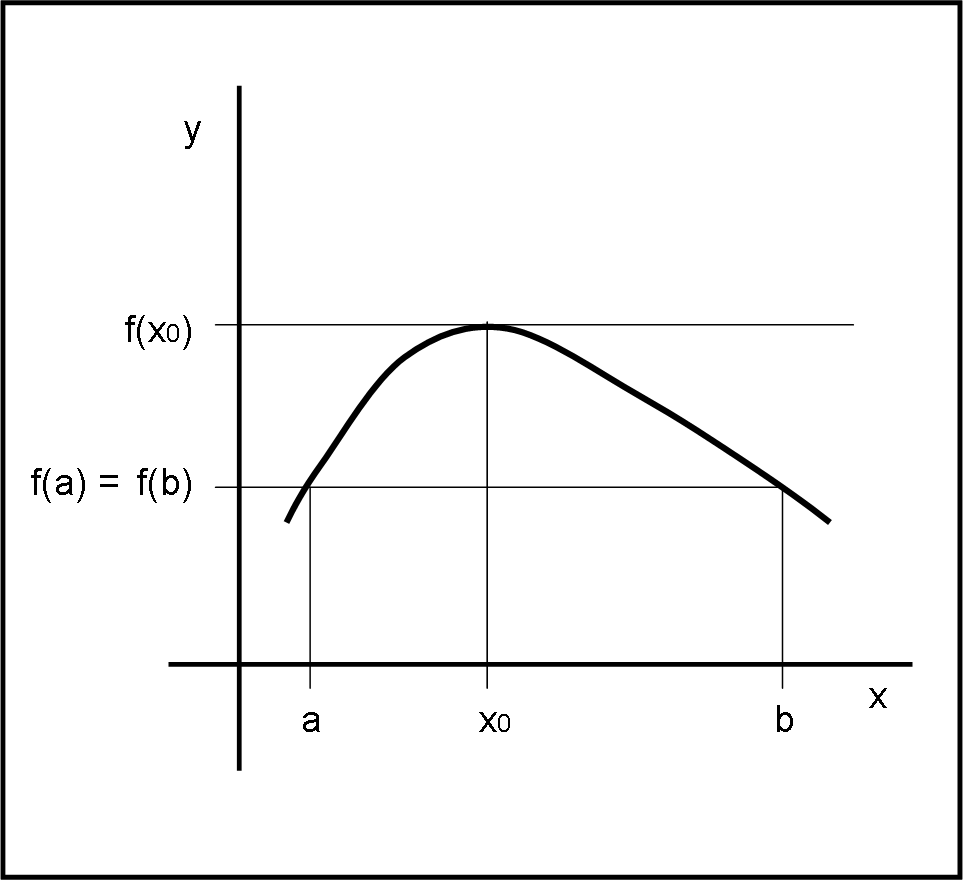
Come appena detto, la funzione deve essere continua (senza punti peculiari o salti improvvisi) e derivabile. La seconda assunzione evita il caso della retta congiungete a con b, dato che la derivata sarebbe sempre nulla.
Ne segue che qualsiasi cosa faccia la funzione nell’intervallo (a,b), essa, partendo da f(a), deve tornare a f(b) = f(a). Non è difficile concludere che, se deve essere “curva”, deve esistere almeno un punto di massimo e/o minimo all’interno dell’intervallo (a,b). Ma un punto di massimo e/o di minimo deve anche avere una x0 tale che f '(x0) = 0.
Sembra una vera sciocchezza (ma sapeste quanti teoremi fondamentali dell’analisi matematica hanno questa apparenza…) e non possiamo certo complicare ciò che è semplice. Tuttavia, da questo teorema ne segue uno leggermente più complicato che prende il nome di teorema di Lagrange. Esso può essere considerato una generalizzazione di quello di Rolle. Il suo enunciato è il seguente:
Se una funzione f(x) è continua e derivabile nell’intervallo (a,b) ed è inoltre f(a) ≠ f(b), allora esiste sicuramente un punto di ascissa x0 nell’intervallo (a,b) tale che la tangente alla funzione in quel punto sia parallela alla congiungente i punti P(a,f(a)) e Q(b,f(b)).
Lo vediamo rappresentato in fig. 2.
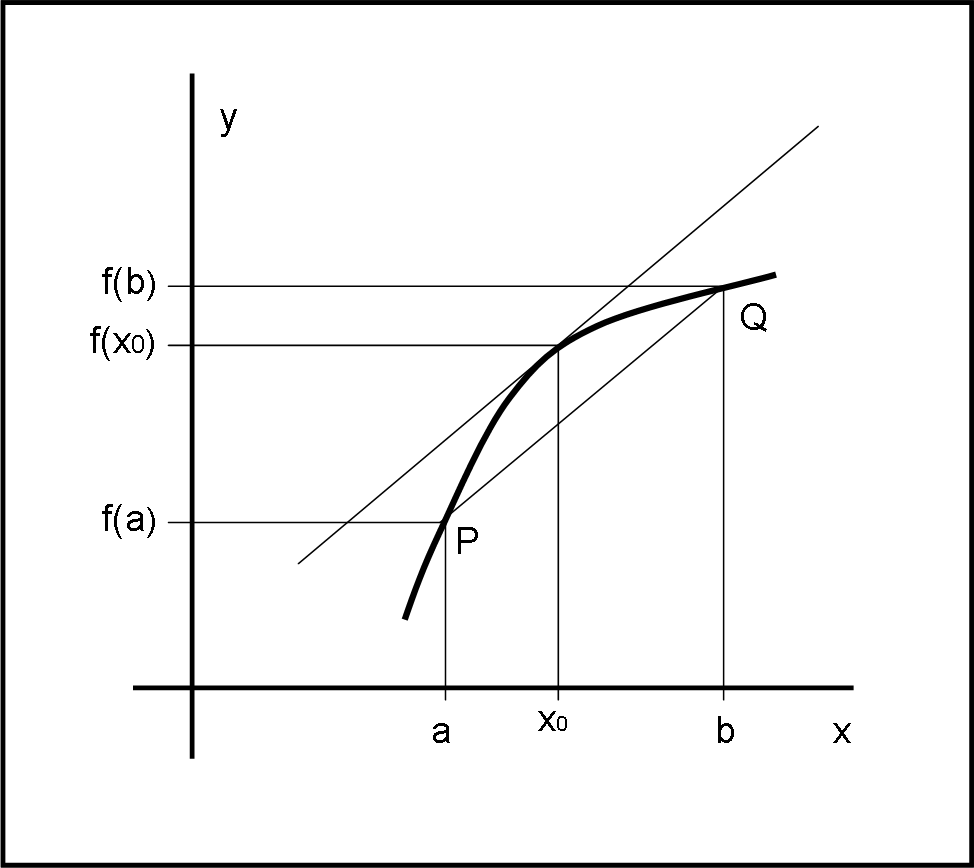
Beh… potremmo facilmente dire che non è altro che il teorema di Rolle “ruotato”. In realtà, è proprio così, ma la dimostrazione è abbastanza laboriosa. Accettiamola per buona, dato che il risultato è abbastanza intuibile. Più interessante è tradurlo in una semplice formula:
f ’(x0) = (f(b) – f(a))/(b – a) …. (1)
Che dice, praticamente, che la tangente in (x0, f(x0)) è parallela alla congiungente P(a, f(a)) con Q(b,f(b)). Infatti, la derivata prima non è altro che il coefficiente angolare della tangente in x0.
Questa formula è proprio quella che ci serve per introdurre la serie di Taylor…
La funzione sia definita e derivabile indefinitamente nell’intervallo (a,b), ossia esistano tutte le sue derivate successive. La (1) può essere applicata all’intervallo (x0, x), interno ad (a,b), diventando:
(f(x) – f(x0))/(x – x0) = f ’(x1) …. (2)
Dove x1 è compreso tra x0 e x, ossia x0 < x1 < x
Per le ipotesi di partenza, possiamo dire che f ’(x1) dipende solo e soltanto dall’intervallo (x, x0). Infatti, se cambiassi gli estremi, cambierebbe anche il punto in cui la tangente è parallela alla retta che collega i due estremi e di conseguenza anche il coefficiente angolare della stessa tangente.
f ’(x1) può essere considerata composta da due parti, una costante e una variabile. Come valore costante prendiamo proprio f ’(x0) e chiamiamo ε la parte variabile, ossia:
f ’(x1) = f ’(x0) + ε
La (2) diventa:
(f(x) – f(x0))/(x – x0) = f ’(x0) + ε
f(x) = f(x0) + (x – x0)(f ’(x0) + ε)
f(x) = f(x0) + (x – x0) f ’(x0) + (x – x0)ε …. (3)
Ma che tipo di funzione può essere questa ε ?
Di sicuro non può essere una costante dato che se derivassimo la (3) sotto questa ipotesi avremmo:
f ’(x) = 0 + f ’(x0) + ε = f ’(x0) + ε
Questa “banale” relazione ci dice che ε deve annullarsi nel momento in cui x = x0. E’ l’unico modo perché si ottenga f '(x0) = f ’(x0)!
Perché questo possa succedere, la via più ovvia è che ε sia funzione di x – x0, ossia:
ε = C2(x – x0) …. (4)
con C2 costante (vi state accorgendo che cerchiamo di inserire fin da subito i coefficienti della serie…). Il pedice 2 ha una sua ragione d’essere, come vedremo tra poco.
Sostituiamo la (4) nella (3) e otteniamo:
f(x) = f(x0) + (x – x0) f ’(x0) + C2(x – x0) (x – x0)
f(x) = f(x0) + (x – x0) f ’(x0) + C2(x – x0)2 …. (5)
Non ci resta adesso che derivare di nuovo la (5), per cercare di determinare il valore di C2.
f ’(x) = f ’(x0) + 2C2(x – x0)
(f ’(x) – f ’(x0))/(x – x0) = 2C2
Ma, applicando di nuovo il teorema di Lagrange alla funzione f ’(x) (continua e derivabile per definizione) si ha:
(f ’(x) – f ’(x0))/(x – x0) = f ”(x2)
da cui:
C2 = f ”(x2)/2 …. (6) (il pedice 2 corrisponde al grado della derivata)
Ovviamente, con x0 < x2 < x
Sostituiamo la (6) nella (5)
f(x) = f(x0) + (x – x0) f ’(x0) + f ”(x2)(x – x0)2/2 …. (7)
f(x) - f(x0) - (x – x0) f ’(x0) = f ”(x2)(x – x0)2/2 …. (8)
Il secondo membro della (8) non è altro che ciò che manca al primo membro per arrivare fino alla funzione originaria. In altre parole l’errore che si commette approssimando la curva con la tangente in x0.
Chiamiamo questo “errore”, resto di Lagrange e lo indichiamo con R2:
R2 = f ”(x2) (x – x0)2/2
Speravate di essere alla fine? Purtroppo no… siamo solo all’inizio o quasi (ecco perché i tre-quattro asterischi dell’articolo, anche se le operazioni e i concetti non sono difficili).
Per adesso possiamo solo dire che l’errore commesso è di ordine superiore alla funzione che abbiamo usato come approssimazione. In particolare abbiamo anche trovato che dipende dalla derivata seconda…
Non ci resta che ripetere quanto fatto finora. Prima, però, digerite bene questa prima parte...
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






16 commenti
Leggendo questo articolo mi sembra di essere ritornato il giovane capellone entusiasta del primo anno di università. Potresti anche farmi rispuntare i capelli, già che ci sei?
facilissimo Massimo... basta volerlo, fortissimamente volerlo!!!
Grazie Vincenzo, fin qui ben spiegato!
Caro Enzo, ho ragionato parecchio su questo articolo....
Innanzitutto sul teorema di Lagrange, per cercare di comprenderne meglio il significato ho realizzato due figure...
L'intento è quello di dimostrare che se prendo due punti (A e B) di un tratto di curva continuo e derivabile e traccio una retta che li congiunge, questa traslata diventa la tangente alla curva in un certo punto (C)
Nella prima curva si ha il caso più semplice, quello in cui C rappresenta un punto massimo e f(xa) = f(xb)..... la tangente della curva nel punto di massimo si annulla, ossia il suo coefficiente angolare è uguale a zero (m=0), ossia lo stesso coefficiente angolare della retta che “unisce” A e B ed in questo particolare caso (f(xa) = f(xb)) è parallela anche all'asse x (due rette sono parallele se hanno il medesimo coefficiente angolare m).
Ho anche indicato un segmento h max che unisce il punto C alla perpendicolare della retta che congiunge A e B, che rappresenta la massima distanza tra le due rette.
Nella seconda curva ho disegnato due assi d fittizi (x' e y') al fine di dimostrare che il ragionamento è lo stesso di prima, solo che la tangente ha un coefficiente angolare m diverso da zero, ma sempre identico alla retta che congiunge A e B.
Anche in questo caso il punto C si trova alla massima distanza h max tra le due rette parallele.
http://www.astrobin.com/full/215950/R/
Ovviamente, anche usando le stesse due curve, variando i punti A e B, varia anche il coefficiente angolare m della retta tangente alla curva e la posizione del punto C.
http://www.astrobin.com/full/215950/S/
C'è una frase nel tuo articolo che non mi è molto chiara:
“ f ’(x) = 0 + f ’(x0) + ε = f ’(x0) + ε
Questa “banale” relazione ci dice che ε deve annullarsi nel momento in cui x = x0. E’ l’unico modo perché si ottenga f(x0) = f ’(x0)!”
La prima parte è chiara, ossia che ε deve annullarsi nel momento in cui x = x0, ma non capisco in che senso si ottiene f(x0) = f ’(x0)
Partendo dalla penultima formula (7) ho provato a ragionare su come approssimare meglio la curva, ossia come diminuire ulteriormente l'errore ε (ma non so se il ragionamento è corretto):
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f”(x2)/2 (7)
dove il secondo membro rappresenta l'errore stimato (il resto di Lagrange R2)
R2 = (x – x0)² f”(x2)/2
Ora, prima di proseguire provo ad applicare lo stesso ragionamento fatto con f '(x1) = f' (x0) + ε alla derivata seconda, ossia, fissando come costante la derivata seconda calcolata nel punto f''(x0) (x0 < x2 < x), quindi dovrebbe valere la relazione:
f'' (x2) = f''(x0) + ε
Ovviamente il Teorema di Lagrange, ci dice che:
f'' (x2) = (f '( x) - f '( x0))/(x-x0)
Ossia indica come varia la derivata prima, nell'intervallo tra x ed x0.
A questo punto sostituisco il valore di f'' (x2) = (f''(x0) + ε) nella formula (7):
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f”(x2)/2
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² (f''(x0) + ε)/2
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f''(x0) /2 + (x – x0)² ε 1/2
La nuova funzione ε, non può essere costante, quindi deve dipendere da (x – x0), ed il suo coefficiente deve valere anch'esso qualcosa tipo C3(x – x0), solo che la ε compare come metà ½ ε, quindi:
½ ε = C3(x – x0)
ε = 2C3(x – x0)
Ora non resta che provare a sostituire il valore di ε nell'ultima equazione trovata:
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f''(x0) /2 + (x – x0)² ε ½
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f''(x0) /2 + (x – x0)² 2C3 (x – x0) 1/2
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f''(x0) /2 + C3 (x – x0)³
Per trovare il valore di C3, eseguo la derivata prima:
f'(x) = f’(x0) + 2(x – x0) f''(x0) /2 + 3 C3 (x – x0)²
f'(x) = f’(x0) + (x – x0) f''(x0) + 3 C3(x – x0)²
Eseguo la derivata seconda:
f''(x) = f''(x0) + 6 C3(x – x0)
f''(x) – f''(x0)/(x – x0) = 6 C3
ma per il Teorema di Lagrange
f''(x) – f''(x0)/(x – x0) = f'''(x3)
f'''(x3) = 6C3
C3 = f'''(x3)/6
Infine:
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f''(x0) /2 + C3 (x – x0)³
f(x) = f (x0) + f’(x0) (x – x0) + (x – x0)² f''(x0) /2 + (x – x0)³ f'''(x3)/6
Sembra funzionare, ma è corretto?
Paolo
caro Paolo, tu dici:
"La prima parte è chiara, ossia che ε deve annullarsi nel momento in cui x = x0, ma non capisco in che senso si ottiene f(x0) = f ’(x0)".
Tu hai una relazione del tipo:
f ’(x) = f ’(x0) + ε
E' ovvio che deve ottenersi f '(x0) = f '(x0), ossia la funzione a primo membro calcolata in x0 deve essere uguale a se stessa (al secondo membro). Rimane allora il fastidio di epsilon, che deve annullarsi perché ci sia l'uguaglianza. Tuttavia, abbiamo imposto che epsilon sia non costante e quindi anche diversa da zero, il modo più semplice perché essa diventi zero per x = xo è che lei sia formata da una costante C e da un termine variabile che vada a zero per x = x0, ossia (x - x0).
Per il resto sei sulla strada giusta, ma la funzione non può più essere epsilon, ma un'altra... Il concetto però è abbastanza corretto.
Scusa Enzo,
che f ’(x) = f ’(x0) + ε e che quindi se x= x(0) con ε che si annulla, si ha
f '(x0) = f' (x0) è chiaro (o anche che f(x) = f (x0).... f(x0) = f (x0) ), ma non capisco come la funzione in x0 possa essere uguale alla derivata prima della funzione calcolata in x0, ossia come si ottiene:
f (x0) = f' (x0)
Grazie per la pazienza.
Paolo
Non mi picchiare Paolo
Tutto dipendeva dall'aver perso un apice per strada... adesso è tutto a posto. Poverino... avevi voglia di trovare che f(x0) = f '(x0). Volevo solo scrivere l'ovvietà f '(xo) = f '(xo)!!!
E pensare che questa volta avevo letto e riletto l'articolo molte volte, ma l'apice è scappato lo stesso...
Caro Paolo,
continuo, come ti avevo già detto qualche tempo fa, a provare nei tuoi confronti una "sana invidia"... mi piacerebbe tanto avere il tempo di fare quello che fai te!!
Ma, piano piano, sto facendo più di quanto pensavo fosse possibile e sono moderatamente soddisfatta
Salve,ho trovato questa "costruzione rigorosa" della formula di taylor cercando su google,mi sembra molto chiara.Non ho capito però come mai ε = C2(x – x0),in questo modo è vero che ε si annulla ,ma non si annulla anche quando ε = C2(x2 – x02),magari qualcuno di buon cuore potrebbe spiegarmi il motivo per cui si sceglie proprio (x – x0)?
Beh... Gianfranco, si prende sempre la funzione più semplice che soddisfi i bisogni
Un'altra cosa,non ho ben capito Perchè C2,C3 e via dicendo,sono costanti.Quindi essi sono valori che non dipendono da x.Se sono costanti quindi anche f''(x2) ,f'''(x3) ecc. Dovrebbero essere costanti ?
Grazie in anticipo
ovviamente sì... sono le derivate calcolate in un punto... f"(x) è variabile , ma diventa costante se la calcolo in x2 e via dicendo...
Mi scusi,ma f''(x2) è costituito da una parte variabile che dipende da x e una parte costante(f''(x0)), questo non significa che al variare della x anche f''(x2) varia?
Mi scuso se disturbo
sì, ma è una costante che varia al variare di x2...
y(x) è una funzione, ma y(x0) è un ordinata ben definita, diversa, però, per ogni x0
"... con C2 costante (vi state accorgendo che cerchiamo di inserire fin da subito i coefficienti della serie…). Il pedice 2 ha una sua ragione d’essere, come vedremo tra poco..."
Grazie,quindi f''(x2) ecc. sono costanti poichè a differenza di f''(x)(che è la funzione derivata seconda ) , hanno un punto definito sull'asse delle ordinate,giusto?
esattamente, è una costante che però varia al variare di x2