Dopo aver introdotto i massimi, i minimi e i flessi orizzontali in modo molto preliminare, è giunta l’ora di affrontarli più accuratamente attraverso le derivate successive di una funzione. Ci arriveremo lentamente in modo da comprenderne appieno il significato sia matematico che geometrico.

Riprendiamo brevemente quanto discusso nella Lezione 24.

Ricordiamo che i minimi, i massimi e i punti di flesso orizzontale di una funzione sono quei punti in cui la tangente alla funzione è orizzontale, ossia dove la derivata è zero. In particolare, un minimo è un punto in cui la funzione raggiunge il valore più basso in un certo intervallo di x. Un massimo è un punto in cui la funzione raggiunge il valore più alto in un certo intervallo di x. Un flesso orizzontale è un punto in cui la funzione attraversa la tangente. Si possono anche collegare facilmente alla concavità della curva. Nei minimi la curva sta sopra la tangente e la concavità è positiva. Nei massimi sta sotto e la concavità è negativa. Nei flessi orizzontali la concavità cambia di segno.

Come si agisce praticamente? Ripetiamo ancora tutta la procedura, dato che è meglio ribadire gli stessi concetti più volte (fidatevi…).

Consideriamo una funzione y = f(x). Sappiamo che potrebbero esistere  punti particolari che annullano la sua derivata prima. Immaginiamo che x₀ sia l’ascissa di uno di questi punti P. Per lei vale:

f ’(x₀) = 0

L’ordinata del punto si ricava dalla funzione di partenza inserendo al posto di x il valore di x₀

y₀ = f(x₀)

Cosa vuol dire che la derivata si annulla nel punto (x₀,y₀)? Che la tangente alla funzione nel punto P è orizzontale, ossia ha il coefficiente angolare m uguale a zero (scusate l’ennesima ripetizione).

Ricapitoliamo meglio cosa capita alla curva prima e dopo il punto particolare.

Se la funzione prima decresce e poi cresce vuole anche dire che siamo in presenza di un minimo.

Se la funzione prima cresce e poi decresce vuol dire che siamo di fronte a un massimo.

Se la funzione cresce sia prima che dopo si ha un flesso orizzontale ascendente.

Se la funzione decresce sia prima che dopo si ha un flesso orizzontale discendente.

Potremmo, teoricamente, fermarci qui. Tuttavia, la matematica vuole tenere conto di tutti i casi possibili e quindi preferisce trovare un  metodo alternativo che possa darci maggiori informazioni sui punti trovati. Accettiamo quindi con pazienza e fiducia la possibilità di metodi alternativi.

Il metodo descritto precedentemente corre, per esempio, dei rischi

Noi, infatti, non sappiamo ancora con che curva abbiamo a che fare e… siamo proprio sicuri di aver scelto, in modo corretto, il punto prima e il punto dopo il minimo? Vi faccio un esempio molto indicativo. Ammettiamo che la nostra curva sia molto complicata e che abbia tanti massimi, minimi e flessi. Può capitare quanto riportato in Fig. 1.

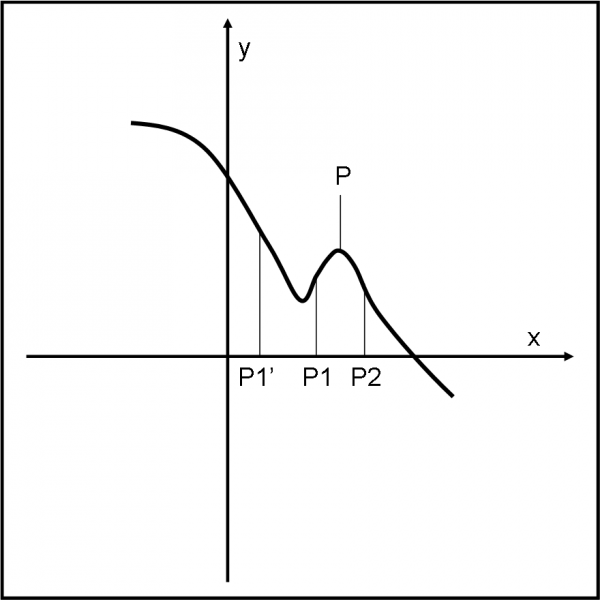
Stiamo studiano il punto P, dato che in esso si annulla la derivata. Prendiamo un punto prima e uno dopo e calcoliamo la funzione. Se scegliamo P₁ e P₂, tutto bene. Sono entrambi con ordinata minore di quella di P e concludiamo giustamente che P è un punto di massimo. Tuttavia, se scegliessimo P₁’ e P2, cosa concluderemmo? Il primo ci direbbe che la sua ordinata è maggiore di quella di P e il secondo che l’ordinata è minore di P. Conclusione: è un punto di flesso discendente. E sbaglieremmo completamente!

Perché abbiamo sbagliato? Perché non possiamo sapere a priori che tra P₁’ e P₁ c’è o non c’è un altro punto particolare (di massimo) che ribalta tutti i risultati. Normalmente, questa situazione non capita, dato che avremmo già trovato anche questo punto particolare annullando la derivata, ma non si sa mai ed è meglio evitare possibili confusioni e fraintendimenti…

Molto meglio trovare qualche sistema un po’ più sicuro e meno rischioso.

Torniamo a parlare di tangente e vediamo se ci dà qualche buona idea. Nei punti particolari essa deve essere zero. Cosa succede prima e dopo di quel punto?

Consideriamo la Fig. 2.

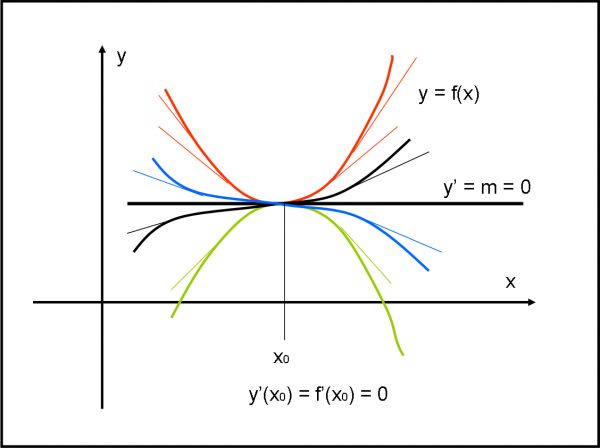
Nel caso di un minimo (curva rossa), prima del punto critico la tangente deve essere diretta verso il basso, ossia deve avere un coefficiente angolare m negativo. Tuttavia, a mano a mano che ci avviciniamo al minimo, il valore di m diventa sempre meno negativo e quindi possiamo dire che m sta crescendo. Poi arriva al minimo e m si annulla (tangente orizzontale). Dopo il minimo il coefficiente angolare riprende a salire e diventa, ovviamente, positivo. La variazione di m non è altro che la variazione di y’ in funzione di x.

Nel caso di un massimo (curva verde), la tangente inizia con un coefficiente angolare maggiore di zero, poi si annulla e quindi inizia a decrescere diventando negativo.

Nel caso di un flesso orizzontale ascendente (curva nera) la tangente inizia con un coefficiente positivo, poi si annulla e dopo ricomincia a crescere con coefficiente sempre positivo.

Infine, nel caso di un flesso orizzontale discendente (curva blu) succede il contrario. Il coefficiente angolare della tangente (la derivata) è negativo, poi si annulla e poi riprende a essere negativo.

Potremmo limitarci a queste considerazioni e studiare il segno della derivata, prima e dopo il punto particolare. Tuttavia, ci sono un paio di problemi. Innanzitutto è un metodo abbastanza laborioso che necessita di eseguire delle disequazioni. Inoltre, porterebbe a un risultato apparentemente decisivo, cosa che in realtà non è così ovvio, come vedremo con funzioni un po’ complesse.

Conviene cercare un’ulteriore alternativa. Rimaniamo comunque nella Fig. 2. Come abbiamo già detto, la tangente alle varie curve ha come coefficiente angolare  (variabile) la derivata della funzione nei vari punti considerati. Possiamo, quindi, dire che la derivata (ossia m) è una funzione di x. Possiamo, perciò disegnarla tranquillamente in un sistema cartesiano che abbia sempre la x come ascissa, ma che abbia, questa volta, il coefficiente m come ordinata. In altre parole, l’ordinata è la funzione y’ = f ’(x). Disegniamo le varie curve relative alle derivate delle varie situazioni precedenti, mantenendo il colore, nella Fig. 3. Ovviamente, abbiamo preso curve generiche non sapendo con che funzione stiamo lavorando.

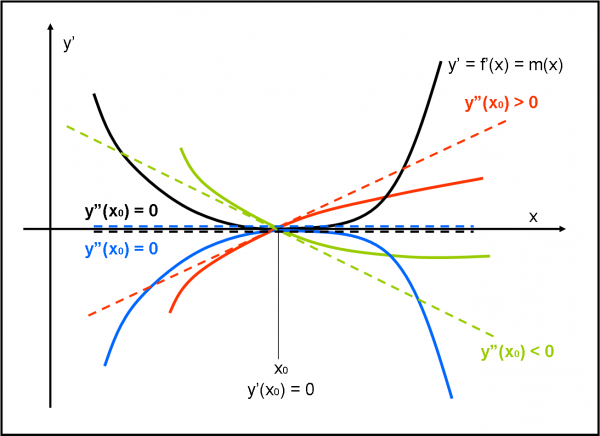
Cosa succede alla derivata della curva rossa. Lo sappiamo già: la derivata continua a crescere passando per y’ = 0 nel punto di ascissa x₀. Nel punto (P x₀,y₀), infatti, la derivata deve annullarsi. Cosa succede alla tangente alla nuova curva f’(x) nel punto P(x₀,y₀)? Beh, la risposta è facile: deve avere un coefficiente angolare positivo, dato che la funzione y’ = f ’(x) è crescente (i coefficienti angolari della tangente in tutti i punti della funzione crescente f ’(x) devono essere tutti positivi).

Diciamo le cose in modo leggermente diverso che ci permette di introdurre un’operazione innovativa. La y’ = f ’(x) = m(x) non è altro che una funzione. Come si può determinare la sua tangente nel punto P(x₀,y₀)? In particolare, come si fa a trovare il coefficiente angolare di questa retta? Basta eseguire la derivata della funzione f ’(x), calcolata nel punto P(x₀,y₀). Ma… fermi tutti! La funzione f ’(x) non è altro che la derivata della funzione f(x) di partenza. Fare la sua derivata  è come fare la derivata della derivata della funzione di partenza. Questa “doppia” derivata ci regala il coefficiente angolare della tangente alla  f ’(x) e quindi  ci dice che se è maggiore di zero il punto deve essere di minimo.

La derivata di una derivata di una funzione prende il nome di derivata seconda della funzione e si può scrivere con diversi simboli. Per adesso chiamiamola y” = f ”(x). Come si calcola? In modo molto semplice: si prende la derivata prima della funzione di partenza e poi si deriva ancora una volta. Si avrà una certa funzione f ”(x). Basta calcolarla nel punto P(x₀,y₀) e vedere che segno ha. Se è maggiore di zero il punto è di minimo. Un sistema, magari faticoso da descrivere a parole, ma veramente immediato e semplice nella pratica, come vedremo nei vari esempi che faremo tra non molto.

Cosa succede alla curva verde? La sua derivata è decrescente e quindi la sua y’(x) avrà una tangente nel punto P(x₀,y₀) con coefficiente minore di zero. Il che vuole dire (per quanto detto poco fa) che la derivata seconda, calcolata nel punto P(x₀,y₀), è negativa.

Le cose si complicano un pochino con i flessi orizzontali. Si complicano a parole, ma permettono una velocissima azione pratica. Prendiamo la curva nera della Fig.2. Abbiamo visto che la sua derivata continua a essere positiva sia prima che dopo il punto P(x₀,y₀). Portata in Fig. 3 la derivata (prima) descrive, allora, una curva che ha ancora una tangente orizzontale nel punto P(x₀, y₀). In altre parole la derivata seconda, calcolata in P(x₀,y₀) è ancora uguale a zero. Quel punto annulla sia la derivata prima che la seconda.

Come facciamo a risolvere la situazione? Ovviamente, basterebbe studiare il segno della derivata seconda a sinistra e a destra.  Ma, se vogliamo fare i “fini”, potremmo descrivere la funzione derivata seconda nella Fig. 4 e calcolare la derivata terza nel punto P(x₀,y₀). In altre parole, facciamo la derivata della derivata della derivata della funzione di partenza. Se questa è maggiore di zero, vuol dire che finalmente la tangente alla derivata seconda non si annulla in  P(x₀,y₀) e ha un coefficiente angolare positivo. In questo caso è ovvio che siamo di fronte a un flesso ascendente. Basta, perciò, calcolare la derivata terza per decidere che tipo di flesso orizzontale è.

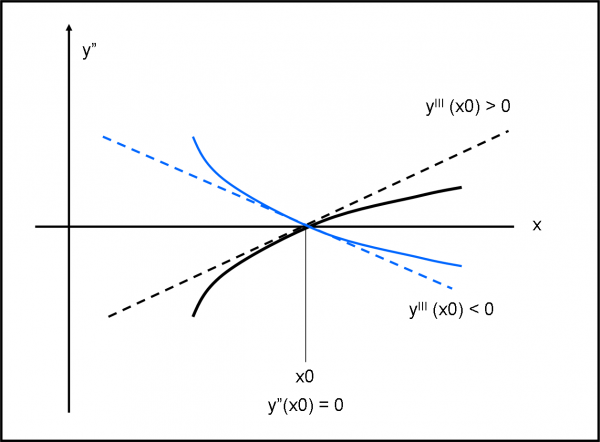
Ovviamente non dobbiamo calcolare la derivata terza in  punti che si sono già dimostrati massimi o minimi, ossia in punti che hanno già la derivata seconda (calcolata in P) diversa da zero!

Vale, ovviamente, un discorso analogo, con i segni cambiati, nel caso del flesso orizzontale discendente.

L’uso della derivata terza è, però, poco usato e si preferisce guardare la concavità della curva prima e dopo il punto che annulla anche la derivata seconda.

Per come è stata ricavata la derivata seconda, essa ci dice com’è la concavità della curva. Se essa è positiva la concavità è diretta verso l’alto, se essa è negativa la concavità è diretta verso il basso. Questo risultato l’abbiamo ottenuto trattando i minimi e i massimi. Nel primo caso le tangenti vanno prima verso il basso e poi verso l’alto: la curva che “inviluppano” ha la forma di una conca. Nel secondo caso vale il contrario e la curva inviluppata forma un monte, ossia una conca al contrario. Mostriamo queste semplici constatazione in Fig. 5, dato che ci verranno molto utili per i flessi obliqui.

Se abbiamo un punto di flesso orizzontale, basta, perciò, vedere che segno ha la derivata seconda per valori minori e maggiori di x₀. Se prima è minore e poi maggiore di zero, abbiamo un flesso orizzontale ascendente. Se è prima maggiore e poi minore di zero abbiamo un flesso orizzontale ascendente (Fig. 6).

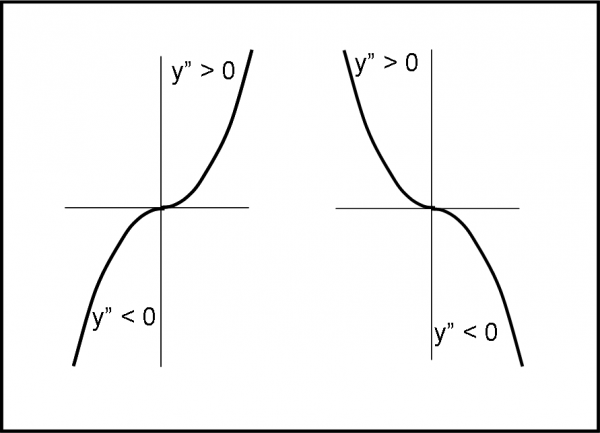
Nei nostri esempi vedremo di usare entrambi i metodi, a seconda dei casi. In generale, non spaventatevi di tutte queste parole che rischiano di creare confusione. Esse ci danno un primo quadro generale concettuale. Passando agli esempi le cose si semplificheranno di molto e si potrà capire molto meglio la parte descrittiva precedente.

Ridendo e scherzando, abbiamo introdotto le derivate successive di una funzione.

Potevamo farlo in modo ben più semplice, ma -secondo me- troppo “meccanico” e sterile… In questo modo l’abbiamo costruita passo dopo passo, sia matematicamente che geometricamente.

In realtà, cosa basta fare? Prendere la derivata prima e derivarla nuovamente come se fosse una nuova funzione.

Ad esempio:

y = x³ + 9x² + 2x - 2

La derivata prima è

y’ = 3x² +  18x + 2

La derivata seconda è la derivata di y’, ossia:

y” = 6 x + 18

e così via …

y^III = 6

y^IV = 0

Ragioniamo ancora un po’ sulla derivata seconda. Non possiamo concederle così poco tempo, dato il suo interesse enorme in fisica…

Possiamo scriverla in vari modi…

y”, y^II, f ”(x), e anche d²y/dx²

Nella descrizione dei problemi fisici, io preferisco, generalmente, l’ultima scrittura perché spiega abbastanza bene l’operazione che è stata svolta. Seguitemi:

d(dy/dx)/dx = (d/dx)/(dy/dx)  = (d/dx)² y = d²y/dx²

Ricordiamo che questa resta, comunque, una notazione e non una vera operazione. Si potrebbe anche ricavare eseguendo il limite del rapporto incrementale della derivata prima… ma direi che possiamo anche farne a meno.

Prima di andare avanti e studiare i punti di flesso obliquo, vorrei non perdere il filo con i suoi risvolti pratici e applicativi nella fisica. La più famosa derivata seconda è molto importante, dato che è nientemeno che l’accelerazione!

Ragioniamoci un po’ sopra…  sappiamo che la variazione rispetto al tempo della posizione di un punto non è altro che la velocità. Ossia la velocità è la derivata dello spostamento del punto rispetto al tempo. Essa ci dice quanto il punto di sposta nell’unità di tempo. Si scrive normalmente in modo vettoriale:

v = ds/dt

Tuttavia, la velocità, ossia la tangente, può variare da punto a punto e siamo, perciò, interessati a studiare come varia questa … variabile. La variazione della velocità rispetto al tempo è ciò che chiamiamo accelerazione a. Vale quindi la relazione:

a = dv/dt

Ma

v =ds/dt

Sostituendo:

a = d(ds/dt)/dt = d²s/dt²

L’accelerazione non è altro che la derivata seconda della posizione rispetto al tempo

Concludiamo questa lezione riassumendo le operazioni da fare per determinare i massimi, i minimi e i flessi orizzontali di una funzione.

Si annulla le derivata prima e si cercano i valori di x che l’annullano. Si calcola la derivata seconda nel punto che annulla la derivata prima. Se essa è positiva si ha un minimo, se è negativa si ha un massimo. Se è uguale a zero si calcola la derivata terza. Se essa è maggiore di zero nel punto che annulla la derivata prima si ha un flesso orizzontale ascendente. Se essa è minore di zero si ha un flesso orizzontale discendente.

Questa regola non parla ancora di flessi obliqui ed è solo un’approssimazione per funzioni abbastanza semplici. Vedremo che le derivate possono anche andare più avanti e la regola generalizzarsi. Useremo molti esempi per aiutare meglio a capire le varie soluzioni possibili. Le funzioni stanno per dare spettacolo!

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica