Categorie: Matematica
Tags: flessi obliqui studio di polinomi
Scritto da: Vincenzo Zappalà
Commenti:8
27. Flessi obliqui e primi polinomi **
Siamo pronti a introdurre i flessi obliqui. Dopo quanto fatto finora, le regole che permettono di determinarli risultano ovvie, anche se bisogna porre attenzione al tipo di concavità che li precede e li segue: non sempre ciò che sale è ascendente! Iniziamo poi con lo studio dei polinomi più semplici…
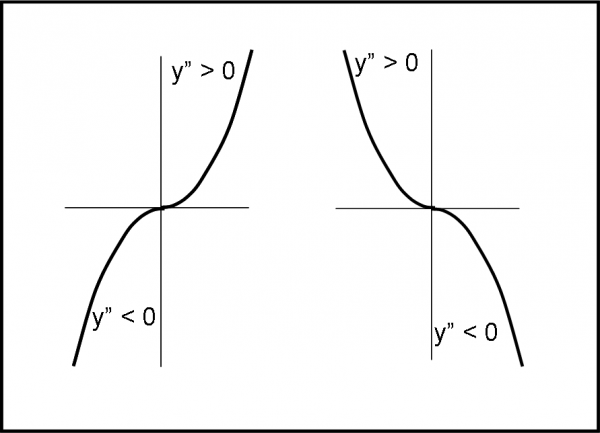
A questo punto, diventa abbastanza semplice introdurre i flessi obliqui. Per meglio definirli riprendiamo un’altra caratteristica dei flessi in genere. A parte il fatto che sono capaci di annullare la derivata prima (quando sono orizzontali) essi sono ancora più caratterizzati dal fatto di annullare la seconda. Ora sappiamo bene cosa vuol dire annullare la derivata seconda: passare da curva con concavità positiva o negativa a concavità opposta. In altre parole, la tangente alla funzione nel punto di flesso deve attraversare la curva descritta dalla funzione. Quest’ultima è sicuramente la definizione più completa e generale.
Possiamo anche dire che in un flesso orizzontale ascendente la curva attraversa la tangente partendo dal di sotto, mentre in un flesso orizzontale discendente la curva parta dal di sopra. Non vi sono alternative. L’uguaglianza tra derivata prima e seconda (entrambe uguali a zero), fa, però, sì che nel caso di flesso orizzontale, il cambiamento di concavità comporti anche una aumento del valore della funzione e viceversa, come si vede bene nella solita Fig. 1. Non facciamoci, però, ingannare da questa analogia che capita solo nel flesso orizzontale!
Flessi obliqui
Prendiamo un flesso obliquo qualsiasi (Fig. 2). Qual è la differenza fondamentale rispetto a un flesso orizzontale? In entrambi i casi la tangente alla curva nel punto di flesso attraversa la funzione e divide la concavità positiva da quella negativa. Tuttavia, nel caso del flesso obliquo la tangente non è una retta orizzontale, ma una retta qualsiasi! La derivata prima nel punto di flesso obliquo NON deve essere uguale a zero, se no diventerebbe un flesso orizzontale.
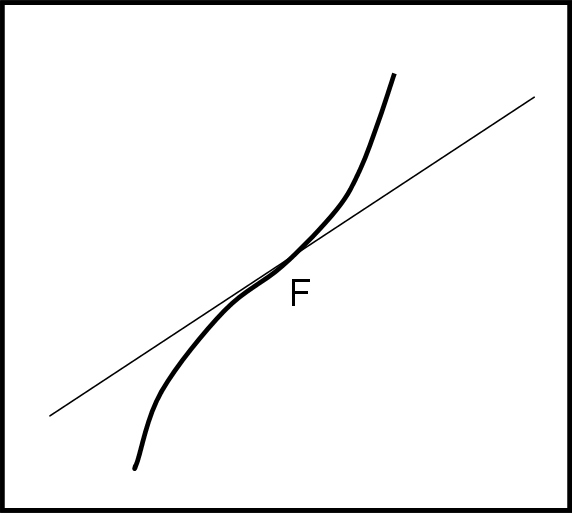
E’ invece obbligatorio che la derivata seconda sia uguale a zero, dato che solo questa caratteristica impone l’attraversamento della curva da parte della tangente nel punto di flesso. Infatti, cosa vuol dire derivata seconda uguale a zero? Che la concavità cambia di segno, ossia passa da negativa a positiva o viceversa.
Non facciamoci però ingannare dall’andamento della funzione prima e dopo un flesso obliquo (o dall'inclinazione della tangente). Anche se la funzione cresce sempre, il flesso può benissimo essere discendente! Lo vediamo molto bene nella Fig.3.
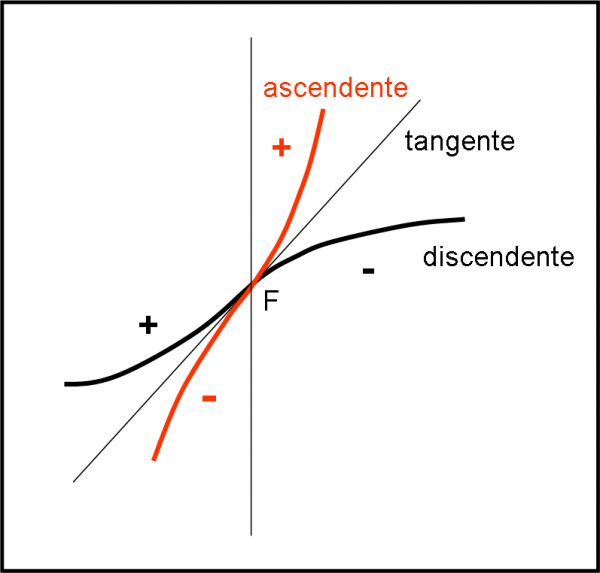
Quello che conta è stabilire la concavità prima e dopo, ossia il segno della derivata seconda o, ancora, vedere se la curva arriva da sopra o da sotto prima dell’attraversamento della tangente. Per essere ascendente un flesso deve vedere la curva arrivarle dal basso e proseguire verso l’alto. E’ discendente se avviene il contrario. La stessa cosa succedeva anche nel caso del flesso orizzontale. Il crescere della curva prima e dopo il flesso, però, adesso non funziona più e va trascurato. Valeva per il flesso orizzontale, ma era solo un caso fortuito dovuto a una tangente orizzontale!
Per definire che un flesso obliquo è ascendente o discendente non bisogna guardare l’apparenza della curva in sé, ma bisogna guardare la concavità prima e dopo o, al limite, se la curva proviene dall’alto o dal basso.
La curva nera ha quindi un flesso discendente, mentre quella rossa ha un flesso ascendente. In entrambi i casi, però, la funzione cresce.
La Fig. 4 è del tutto analoga, ma la tangente ha coefficiente angolare negativo.
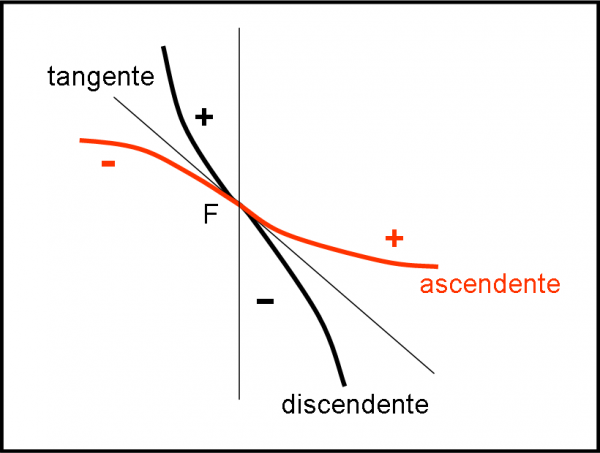
State molto attenti a questo piccolo inganno visivo… quanti studenti ci sono cascati!
In pratica conviene, perciò, fare a meno della derivata terza e decidere il tipo di flesso obliquo studiando il segno della derivata seconda e/o della concavità (è la stessa cosa…).
Siamo proprio giunti al momento di applicare le regole che abbiamo ricavato molto lentamente, ma riflettendoci sopra. Aggiungiamo solo quella relativa ai flessi obliqui.
Si annulla le derivata prima e si cercano i valori di x che l’annullano. Si calcola la derivata seconda nel punto che annulla la derivata prima. Se essa è positiva si ha un minimo, se è negativa si ha un massimo. Se è uguale a zero si calcola la derivata terza. Se essa è maggiore di zero nel punto che annulla la derivata prima si ha un flesso orizzontale ascendente. Se essa è minore di zero si ha un flesso orizzontale discendente. Alternativamente, basta studiare il segno della derivata seconda prima e dopo il flesso. Se prima è negativa e dopo positiva si ha un flesso orizzontale ascendente. Se cambiano i segni si ha un flesso orizzontale discendente.
Si annulla la derivata seconda. Le soluzioni danno i flessi della funzione. Quelli obliqui sono punti in cui la derivata prima è diversa da zero. Per vedere se sono ascendenti o discendenti ci si deve affidare, come si poteva fare anche per i flessi orizzontali, allo studio del segno della derivata seconda o della concavità. Non fidarsi del segno della funzione o dell’inclinazione della tangente nel punto di flesso.
Quanto detto è riassunto nella Fig. 5.
Via con gli esempi
Bene… adesso possiamo incominciare a divertirci con tanti esempi di funzioni che hanno vari tipi di punti particolari. Li eseguiremo insieme e vedremo che alcune soluzioni possono essere interpretare in modo più generale. Alla fine, ci renderemo conto che la regola, prima descritta, è ancora insufficiente per funzioni più complicate, ma che la sua estensione è facilissima.
Occupiamoci dei polinomi, che abbiamo già vivisezionati in un lungo articolo a loro dedicato.
Polinomi di primo grado
Il polinomio più semplice è ovviamente quello di primo grado, ossia quello in cui compare solo la x. beh… lo conosciamo molto bene, dato che non è altro che la retta:
y = ax + b …. (1)
Facciamo finta di essere veramente alle prime armi e cerchiamo se la retta ha punti critici. Ovviamente la nostra regola si blocca subito! Calcoliamo la derivata prima:
y’ = a
La derivata non solo non si annulla mai, m è già una costante, ossia la tangente alla “curva” retta è sempre la stessa. Anzi, è proprio la retta stessa. E’ inutile andare avanti nello studio di questa funzione un po’ troppo elementare e un po’ troppo conosciuta!
Polinomi di secondo grado
y= ax2 + bx + c …. (2)
Deriviamo la funzione e poniamo uguale a zero la derivata:
y’ = 2ax + b = 0
vi è una e una sola soluzione, dato che l’equazione è di primo grado. In particolare:
2ax1 + b = 0
x1 = -b/2a …. (3)
Sostituendo x1 nella funzione di partenza, abbiamo la y1 corrispondente al punto particolare P
y1 = a(-b/2a)2 + b (-b/2a) + c = ab2/4a2 – b2/2a + c = b2/4a – b2/2a + c = (b2 - 2b2)/4a + c
y1 = -b2/4a + c …. (4)
E’ un minimo, un massimo o un flesso orizzontale?
Basta fare la derivata seconda e poi calcolarla nel punto P(x1,y1)
y” = d/dx(y’) = d/dx(2ax + b) = 2a + 0 = 2a
Possiamo fare alcune considerazioni risolutive
1) La derivata seconda NON si annulla mai (se non per a = 0 che vuol dire tornare alla funzione retta)
2) La derivata seconda, indipendentemente dal punto in cui vogliamo calcolarla, ha sempre lo stesso valore
3) Il suo segno è quello del coefficiente a (del termine di secondo grado).
Possiamo concludere:
Non esistono né flessi orizzontali né flessi obliqui (per averli doveva annullarsi la derivata seconda).
Si ha un solo massimo o minimo e chi decide è il segno del primo coefficiente (a), che è proprio la derivata seconda, indipendentemente dal punto in cui si calcola (è una costante!).
Se a è positivo il punto P è un punto di minimo (derivata seconda positiva, concavità verso l’alto)
Se a è negativo il punto P è un punto di massimo (derivata seconda negativa, concavità verso il basso)
Come avete visto, per questo caso molto semplice, abbiamo potuto facilmente studiare la funzione in modo generale, senza mettere numeri al posto dei vari coefficienti. In realtà lo potremmo fare anche per funzioni più complesse, ma faremmo un po’ di confusione con tutte quelle lettere che si moltiplicano, si dividono, ecc., ecc. Useremo , quindi, esempi numerici, senza dimenticare, però, di generalizzare i risultati, caso per caso.
Torniamo alla nostra funzione, rappresentata da un polinomio di secondo grado completa, (ossia con tutti i termini). Essa non è altro che una parabola (una conica che ben conosciamo) che si muove a destra e a sinistra, sopra e sotto, nel piano cartesiano a seconda del valore dei coefficienti a, b e c.
Continuiamo a ragionare sulle lettere (qui lo possiamo fare con facilità).
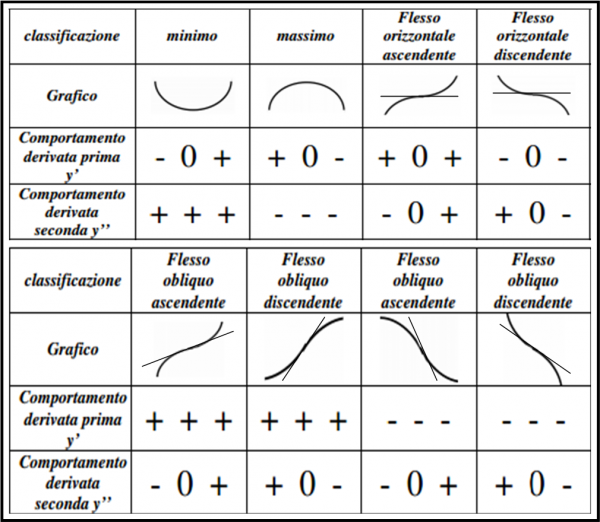
Se manca il termine con coefficiente b (ossia b = 0). La funzione diventa soltanto:
y = ax2 + c
Possiamo subito scrivere il punto particolare, usando la (3) e la (4)
x1 = -b/2a = 0
y1 = -b2/4a + c = c
Il punto di massimo o di minimo si trova sull’asse delle x e la sua ordinata non è altri che il valore del coefficiente c. Ovviamente se a è positivo è un minimo, altrimenti un massimo. Riassumiamo questa soluzione particolare nella Fig. 6. Il minimo o massimo coincide con il vertice se c = 0.
Se b fosse diverso da zero, il vertice inizia a viaggiare in qualsiasi punto del piano cartesiano. Potete fare qualche prova da soli, sia utilizzando le lettere sia creandovi degli esempi numerici.
Limitiamoci a un uno caso numerico, completo, risolvendolo passo dopo passo e vediamo come si inserisce perfettamente nel caso generale.
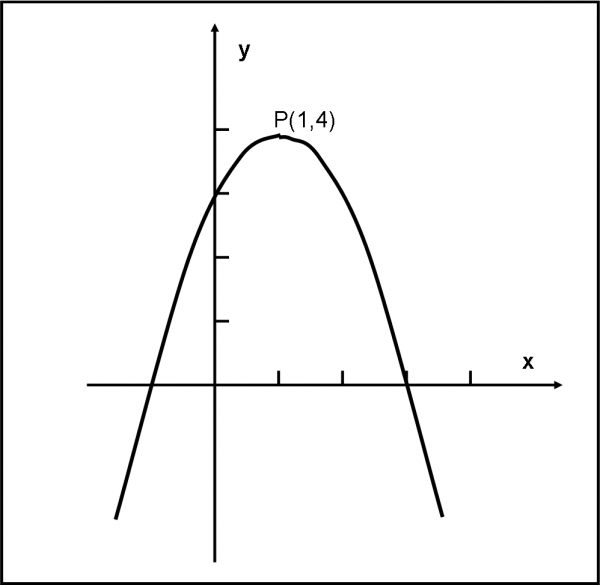
y = - x2 + 2x + 3
y’ = - 2x + 2
- 2x + 2 = 0
2x1 = 2
x1 = 2/2 = 1
y1 = y(x1) = -1 + 2 + 3 = 4
y” = - 2 sempre negativa
Il punto P(1,4) è un punto di massimo
Lo stesso risultato lo otteniamo, ovviamente, utilizzando direttamente la (3) e la (4) con
a = - 1, b = 2, c = 3
Vediamo in Fig. 7 il risultato di questo esempio numerico.
Ovviamente, potete trovare altri punti della parabola (per disegnarla meglio) inserendo diversi valori di x dentro la funzione di partenza…
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






8 commenti
Caro Enzo, diciamo che mi piace complicarmi la vita, ma la curiosità di studiare una funzione che contiene almeno un flesso obliquo ha preso il sopravvento.
Quindi ho provato a realizzare una funzione non troppo complicata la cui derivata seconda si annulla con un certo valore di x, ma in tale punto non si annulla la derivata prima (ossia la condizione che caratterizza un flesso obliquo).
Giocando un po' con i numeri, alla fine ho deciso di usare questa funzione, che soddisfa le condizioni cercate:
y = 2x^3 - 6 x^2
Dato che è mia intenzione disegnare la curva descritta da questa funzione usando ciò che ho appreso nelle ultime lezioni sullo studio delle funzioni, prima di tutto voglio vedere cosa succede con i punti all'infinito:
lim x→ +∞y = lim x→ +∞ 2x^3 – 6x^2 = ∞^3 – ∞^2= +∞
lim x→ -∞y = lim x→ - ∞ 2x^3 – 6x^2 = -∞^3 – ∞^2= -∞
Quindi la curva tende a -∞, con x che tende a -∞ e va verso +∞ con x che tende a +∞.
Guardando i due risultati ed il grado del polinomio risultante, sembra anche che la curva vada più rapidamente verso -∞, rispetto a + ∞.
Dopodiché calcolo i punti di intersezione con gli assi.
Punti in cui la curva taglia l'asse y:
se x=0 y = 2 (0)^3 – 6(0)^2 = 0
Quindi la curva taglia l'asse y una sola volta e proprio all'origine degli assi, punto A(0;0).
Non è poi così strano dato che alla funzione non ho aggiunto un altro numero, tipo y = 2x^3 - 6 x^2 + 3 (in tal caso la curva avrebbe tagliato l'asse y a y=+3).
Punti in cui la curva taglia l'asse x:
se y=0
0= 2x^3 – 6x^2
x^2 (2x - 6) = 0
Ci sono due soluzioni affinché il risultato del prodotto sia uguale a zero:
a) x^2 = 0 x=0
b) 2x - 6 = 0
x= 6/2=3
Quindi la curva taglia l'asse x all'origine degli assi B1(0;0), come già determinato prima, dato che B1 è lo stesso punto A ricavato prima.
La curva, però taglia nuovamente l'asse x in B2 (3;0)
A questo punto voglio vedere se ci sono punti in cui la derivata prima si annulla (Minimi, Massimi e flessi orizzontali):
y = 2x^3 - 6 x^2
y' = 6x^2 – 12x
0 = 6x^2 – 12x
x (6x -12) = 0
di nuovo ci sono due soluzioni che annullano l'equazione di secondo grado:
a) x = 0
b) 6x -12 = 0
x= 12/6 = 2
A questo punto per trovare le coordinate di questi due punti, basta sostituire i valori di x trovati nella funzione iniziale e ricavare il corrispondente valore di y.
a) Se x = 0
y = 2 (0)^3 – 6(0)^2 = 0
b) Se x=2
y = 2 (2)^3 – 6(2)^2 = 16 – 24 = -8
Quindi i due punti cercati sono P1(0;0), ossia l'intersezione della curva con l'origine degli assi e P2(2;-8).
A questo punto per vedere di quali punti si tratta, calcolo la derivata seconda per ognuno dei due punti:
y' = 6x^2 – 12x
y'' = 12x -12
Comincio dal punto P1 (0;0)
y'' = 12 (0) -12
y'' = -12
Dato che la derivata seconda non si annulla non si tratta di un flesso, ma di un minimo o un massimo.
La derivata seconda, però, è negativa, per cui il punto P1 (0;0) è un massimo, ossia il vertice di una concavità negativa della curva coincide con l'origine degli assi.
Passo al punto P2 (2;-8)
y'' = 12 (2) -12
y'' = 24 -12 = +12
La derivata seconda è positiva, per cui il punto P2 (2;-8) è un minimo.
Nessuno dei due punti annulla la derivata seconda, per cui non ci sono flessi orizzontali.
Sono sicuro, però, che esiste almeno un flesso obliquo, dato che ho costruito la funzione di iniziale partendo da questa condizione.
Per cui provo a vedere quale valore di x annulla la derivata seconda:
y'' = 12x -12
0 = 12x -12
x= 12/12 = 1
Quando x è uguale ad 1 la derivata seconda si annulla.
Vediamo cosa succede alla derivata prima sostituendo il valore di x che annulla la derivata seconda, ossia 1:
y' = 6x^2 – 12x
y' = 6 (1)^2 – 12 (1) = 6 -12 = -6
La derivata prima è diversa da zero (la tangente alla curva nel punto di flesso obliquo, ossia dove la curva cambia di concavità, non è parallela all'asse x come nei flessi orizzontali), per cui siamo in presenza di un flesso obliquo.
Inoltre il suo valore ed il suo segno indicano sia il coefficiente angolare della retta tangente al flesso, sia che questo è negativo, ossia m = -6 (dati molto utili per disegnarla).
Si tratta perciò di un flesso obliquo “simile” a quello raffigurato in fig.4 con tangente negativa .
Per capire se il flesso obliquo è ascendente o discendete basta vedere come si comporta la derivata seconda nei pressi del punto di flesso.
Prendo perciò come riferimento due valori di x vicini ad 1 (valore che annulla la derivata seconda), come X1= 0,5 e X2= 1,5 e calcolo la derivata seconda.
Y1'' = 12x -12 = 12 (0,5) – 12 = -6
Y2” = 12 (1,5) -12 = 18 – 12 = 6
Dato che la concavità è negativa prima del flesso e positiva dopo, si tratta di un flesso obliquo ascendente (come quello indicato nella tabella riepilogativa, parte sotto, penultima colonna).
Ora innanzitutto ricavo le coordinate del punto di flesso F, sostituendo nella funzione iniziale il valore di x che annulla la derivata seconda, ossia 1:
y = 2x^3 - 6 x^2
y = 2 (1)^3 - 6 (1)^2
y = 2 - 6 = -4
Il punto di Flesso ha coordinate F (1;-4)
I punti trovati forniscono un'idea di massima sull'andamento della curva, ma per disegnarla preferisco usare anche qualche altro punto.
Innanzitutto aggiungo qualche valore negativo di x, tipo x= -1; x= -0,8; x=-0,6; ed
x = -0,2, anche per vedere come la curva si avvicina al massimo P1 (0;0)(origine degli assi):
y = 2 (-1)^3 - 6 (-1)^2 = -2 - 6(+1) = -8 Q1 (-1;-8)
y = 2 (-0,8)^3 - 6 (-0,8)^2 = -1,024 – 3,84 = -4,86 Q2 (-0,8;-4,86)
y = 2 (-0,6)^3 - 6 (-0,6)^2 = - 0,432 – 2,16 = -2,59 Q3 (-0,6;-2,59)
y = 2 (-0,2)^3 - 6 (-0,2)^2 = -0,016 – 0,24 = -0,256 Q4 (-0,2;-0,256)
qualche punto da massimo a punto di flesso F(1;-4), come x=0,2; x = 0,6, x=0,8.
y = 2 (0,2)^3 - 6 (0,2)^2 = 0,016 - 0,24 = -0224 R1 (0,2;-0,22)
y = 2 (0,6)^3 - 6 (0,6)^2 = 0,432 – 2,16 = -1,728 R2 (0,6;-1,728)
y = 2 (0,8)^3 - 6 (0,8)^2 = 1,024 – 3,84 = -2,816 R3 (0,8;-2,8)
qualche punto da flesso a Minimo P2(2;-8), come x=1,2; x = 1,5, x=1,8.
y= 2 (1,2)^3 - 6 (1,2)^2 = 3,456 – 8,64 = -5,184 S1 (1,2;-5,18)
y = 2 (1,5)^3 - 6 (1,5)^2 = 6,75 – 13,5 = -6,75 S2 (1,5;-6,75)
y = 2 (1,8)^3 - 6 (1,8)^2 = 11,664 - 19,44 = -7,776 S3 (1,8;-7,77)
Infine qualche punto dal Minimo verso l'alto anche oltre il punto B2(03; 0) di intersezione con l'asse x, come x=2.2; x = 2,6, x=2,8; x=3,2; x=3,3.
y = 2 (2,2)^3 - 6 (2,2)^2 = 21,296 - 29,04 = -7,744 T1 (2,2; -7,74)
y = 2 (2,6)^3 - 6 (2,6)^2 = 35,152 – 40,56= -5,408 T2 (2,6;-5,4)
y = 2 (2,8)^3 - 6 (2,8)^2 = 43,904 - 47,04 =-3,136 T3 (2,8;-3,13)
y = 2 (3,2)^3 - 6 (3,2)^2 = 65,536 – 61,44 = +4,096 T4 (3,2; 4,09)
y = 2 (3,3)^3 - 6 (3,3)^2 = 71,874 - 65,34 = + 6,534 T5 (3,3; 6,534)
Ora non resta che tradurre questa sequenza di numeri in una curva, come quella nella figura che rappresenta la funzione y = 2x^3 - 6 x^2
http://www.astrobin.com/full/38903/G/
Spero di non aver commesso errori, ma a giudicare dalla figura sembrerebbe tutto a posto.
Paolo
PS: prima della figura 6 nella frase; “Il punto di massimo o di minimo si trova sull’asse delle x e la sua ordinata non è altri che il valore del coefficiente c. Ovviamente se a è positivo è un minimo, altrimenti un massimo.”
Se non ho frainteso in questo caso il segno della derivata dipende dal coefficiente c e non da a.
caro Paolo,
bravissimo... hai perfettamente compreso la descrizione e con la tua logica sei riuscito a scrivere da solo il capitolo successivo! Quasi, quasi, potresti continuare tu fino agli integrali...
Per quanto riguarda il commento finale: la funzione è di secondo grado senza termine in x. La derivata prima sarà allora una funzione di x, senza più termine noto (la derivata di c va a zero), che quindi si annulla sicuramente per x= 0. la y di questo punto singolare, sarà quindi uguale a c, che determina la posizione. La derivata seconda sarà funzione solo di a (c è sparito e b è già zero di partenza) e quindi è solo il suo segno che decide se è massimo o minimo. Il valore di c decide solo l'ordinata del punto, ma è solo a che decide se è un massimo o un minimo. Ti torna?
Hai ragione sono io che ho frainteso , pensavo ti riferissi all'equazione:
, pensavo ti riferissi all'equazione:
y1 = -b2/4a + c = c con b = 0
Per cui y1 = 0 + c
Se c è negativa il vertice della curva avrà ordinata negativa, se è positivo avrà ordinata positiva, se è uguale a zero, coincide con l'origine degli assi come con la funzione che ho costruito.
Tu invece ti riferivi alla derivata seconda il cui segno dipende solo da a (ossia dal coefficiente angolare), per cui se è negativo (concavità negativa) si ha un massimo, in caso contrario si tratta di un minimo.
Sonio io che ho equivocato.
Paolo
OK!
Ciao. Oggi mi sono imbattuto nella funzione f(x)= x/sqrt(4-x^2) . Svolgendo lo studio di funzione e disegnando la curva sembrerebbe avere un flesso nell'origine degli assi a causa del cambio di concavità ma ricontrollando, la derivata prima e la derivata seconda non si annullano mai. Come spiegarlo allora?
così a occhio posso subito dirti che la funzione ha un asintoto verticale, dato che la y va a infinito per x = 2....
Si questo è subito identificabile ad occhio. Ciò che mi incuriosisce è il fatto di questo cambio di concavità nell'origine degli assi, anche se nonostante ciò la derivata prima e la derivata seconda al numeratore presentano un numero (ciò implica che non si annullano )
caro Francesco,
perché non mi mandi lo svolgimento dei tuoi calcoli e un diagramma grossolano della funzione che trovi? Sarebbe più facile trovare l'inghippo. Come vedi, adesso, puoi anche scrivere in latex o inserire un file...