Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

 

Attraverso tanti calcoli analitici (di media difficoltà, anche se un po' noiosi) si possono ricavare le tre leggi di Keplero partendo dalla legge di gravitazione universale di Newton. Vi è un solo punto critico relativo alla derivazione della traiettoria del corpo orbitante: un'equazione differenziale che comporta il calcolo di un integrale non banale (per noi almeno). Solo in questo caso accettiamo di prendere un risultato per buono... Per dirla in altre parole, risolviamo un problema fondamentale di Meccanica Celeste: il problema dei due corpi.

Ellissi ed equazioni differenziali

Iniziamo un discorso estremamente importante: partendo dalla legge di Newton vogliamo arrivare alle leggi di Keplero. Può sembrare strano, ma è un argomento trattato raramente, anche se è veramente fondamentale, riferendosi al moto di due corpi. In questo primo articolo ricordiamo le coordinate polari, descriviamo un’ellisse e introduciamo un nuovo tipo di equazione, in modo estremamente semplificato.

Conosciamo tutti le tre leggi di Keplero. E se non fosse vero, le richiameremo, comunque, tra non molto. Tuttavia, sappiamo che esse sono state ricavate attraverso le osservazioni dirette, senza preoccuparsi di quale fosse la legge fisica che le originava.

D’altra parte, però, sappiamo anche che la legge di gravitazione universale descritta da Newton ha come ricaduta proprio il moto di un corpo attorno a un altro (o -se preferite- attorno al comune baricentro).

E’, quindi, più che ovvio che uno sia convinto che le leggi di Keplero debbano poter essere ricavate dalla legge di Newton. A prima vista, sembrerebbe una derivazione semplice e, invece, non lo è affatto! Ad esempio, assumendo un moto circolare uniforme, è possibile ricavare quasi immediatamente la terza legge di Keplero, ma ben diversa è la situazione, se ammettiamo orbite ellittiche.

Abbiamo ormai le conoscenze, sia matematiche che fisiche, sufficienti per affrontare analiticamente il moto di due corpi. Ricordiamoci che, se già passassimo ai tre corpi, non avremmo più una soluzione analitica (se non per casi molto particolari). Il problema di due corpi è quindi tutt’altro che una semplice ovvietà.

Conosciamo anche gli integrali e quindi non dovremmo avere alcun intoppo. In realtà, la faccenda è un po’ più complicata, nel senso che per riuscire a svolgere completamente il nostro esercizio è necessario introdurre un’equazione differenziale e risolverla.

Senza spaventarsi troppo, questo vuole anche dire calcolare integrali ben più complessi di quanto visto nei capitoli a loro dedicati nella matematica. Continuare nel calcolo integrale, per riuscire a risolvere quello di cui avremmo bisogno, sarebbe, però, una fatica enorme e necessiterebbe di nozioni sui numeri complessi e altro ancora. Non penso sia il caso di spingersi così avanti con la matematica. Ho deciso, perciò, di accettare come dato di fatto la soluzione di un integrale non certo banale. E’ solo un passaggio, perché tutto il resto è alla nostra portata, ve lo assicuro!

In ogni modo, per i più esperti e/o volenterosi, cercherò un sito dove sia descritta completamente la descrizione della soluzione.

Comunque, per adesso, non pensiamoci, e cominciamo ad affrontare il problema che ci deve portare da Newton a Keplero.

Per fare ciò è necessario richiamare due concetti, uno già conosciuto e uno del tutto nuovo, ma che si collega facilmente a quanto abbiamo appena discusso sul moto uniformemente accelerato. Il primo è l’utilizzo delle coordinate polari, estremamente più utili per il nostro scopo; il secondo è la definizione di un’equazione differenziale (non la sua soluzione…) e una sua immediata applicazione al moto con accelerazione costante.

Iniziamo, quindi, con questi due preliminari, limitati a quanto ci sarà veramente utile.

Vorrei aggiungere che non è facile trovare questa trattazione a livello divulgativo, anche se sembrerebbe di un’importanza enorme. Noi cercheremo di fare delle piccole approssimazioni, del tutto trascurabili, che ci aiuteranno a tenerci sempre su un livello comprensibile a tutti coloro che hanno seguito le lezioni di matematica e un po’ di fisica classica, a livello velocità, accelerazione e momento angolare o poco più.

Coordinate polari: un richiamo e qualche esercizio

Anche se le abbiamo usate spesso, non sono mai state introdotte in modo specifico. Lo facciamo adesso, anche se risultano del tutto ovvie, conoscendo le funzioni trigonometriche più semplici (QUI).

Consideriamo un punto P in un sistema di assi cartesiani. Esso viene individuato dalle due coordinate x e y, come rappresentato in Fig. 1.

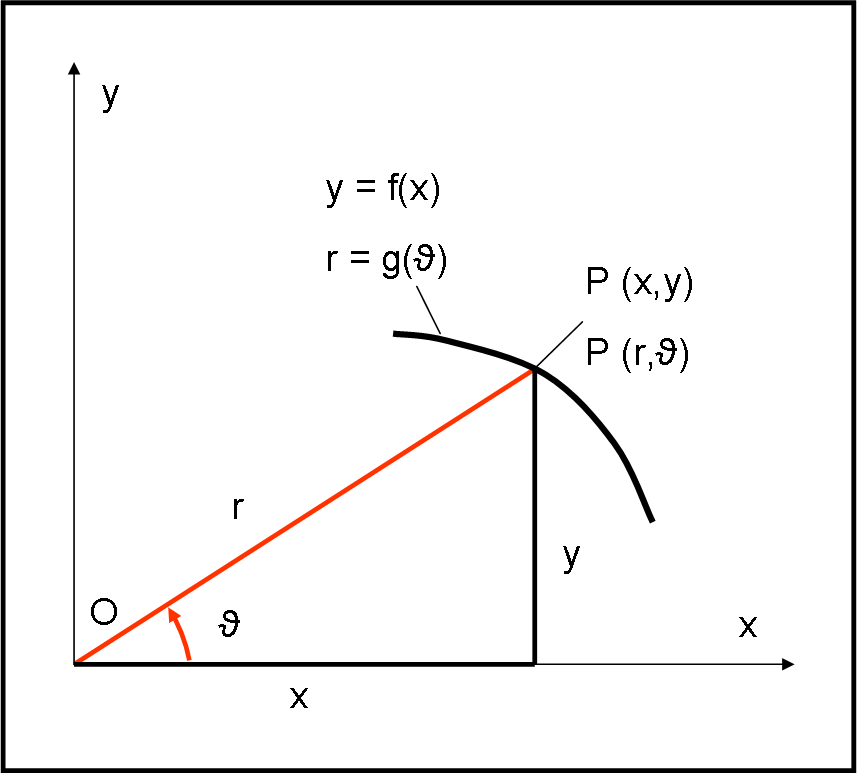
Lo stesso punto, però, può anche essere individuato con altre due coordinate: la distanza dall’origine r e l’angolo ϑ tra asse x e segmento r. Il passaggio da un sistema all’altro è banale, ricordando le funzioni trigonometriche di base.

x = r cos ϑ

y = r sin ϑ

Ne deriva che una funzione in coordinate cartesiane y = f(x) diventa in coordinate polari r = g(ϑ).

Facciamo qualche semplice esempio.

Consideriamo la retta passante per l’origine:

y = mx

In coordinate polari diventa semplicemente:

ϑ = c                      (c costante)

Ovviamente l’angolo costante c non è altro che l’angolo la cui tangente vale m (coefficiente angolare)

La circonferenza con centro nell’origine e raggio R, in coordinate cartesiane, è:

x² + y² = R

In coordinate polari non è altro che:

r = R

Infatti, per qualsiasi valore di ϑ, la distanza r rimane sempre la stessa ed è uguale al raggio.

Consideriamo una generica retta non passante per l’origine (y = mx + n). Utilizziamo la Fig. 2.

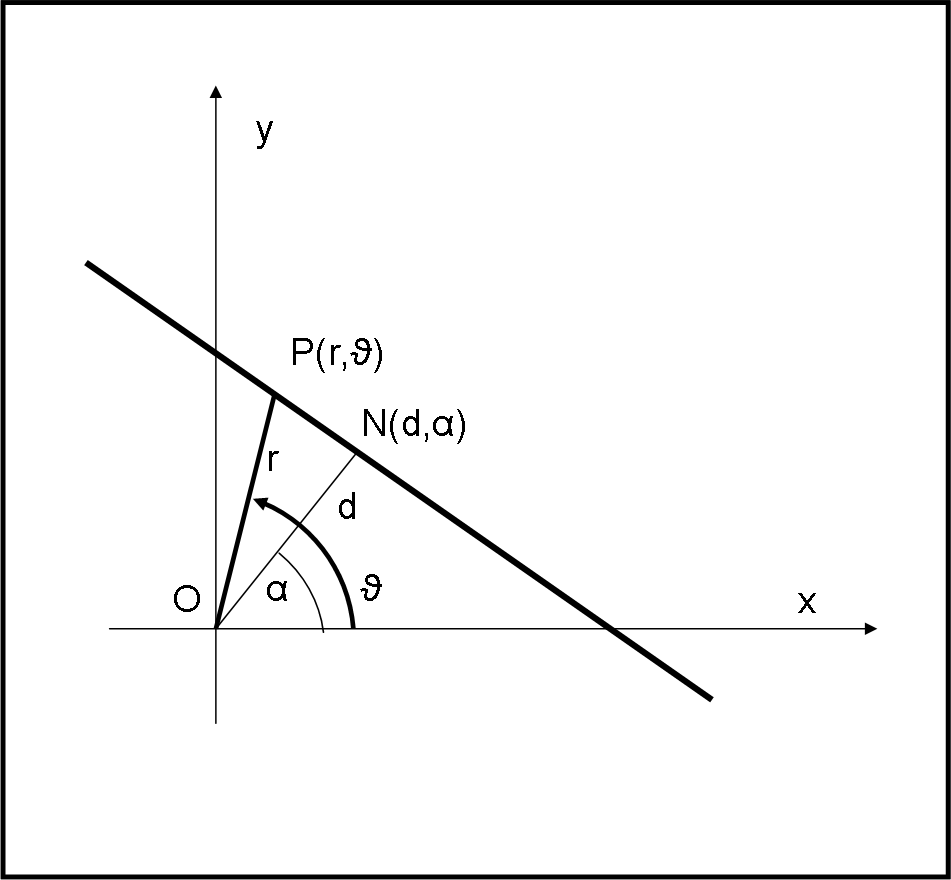
Tracciamo dall’origine la perpendicolare alla retta e sia N il punto d’intersezione. Le coordinate polari di N sono d e α. Consideriamo un punto P qualsiasi della retta che ha coordinate r e ϑ. Dal triangolo rettangolo ONP si ha subito:

d = r cos (ϑ – α)

e, quindi:

r = d/cos (ϑ – α)        dove d e α sono, ovviamente, costanti.

Insomma, è facile capire che in alcuni casi è più semplice usare le coordinate cartesiane e in altri le coordinate polari.

A noi interessa scrivere l’equazione di un ellisse considerando come origine uno dei fuochi. In questo caso sono decisamente più utili le coordinate polari, anche se dobbiamo fare qualche “noioso” passaggio per determinarle. Poi, però, tutto sarà più semplice.

Coordinate polari: l’equazione dell’ellisse

Partiamo dall’equazione in coordinate cartesiane riferite al centro dell’ellisse (Fig. 3):

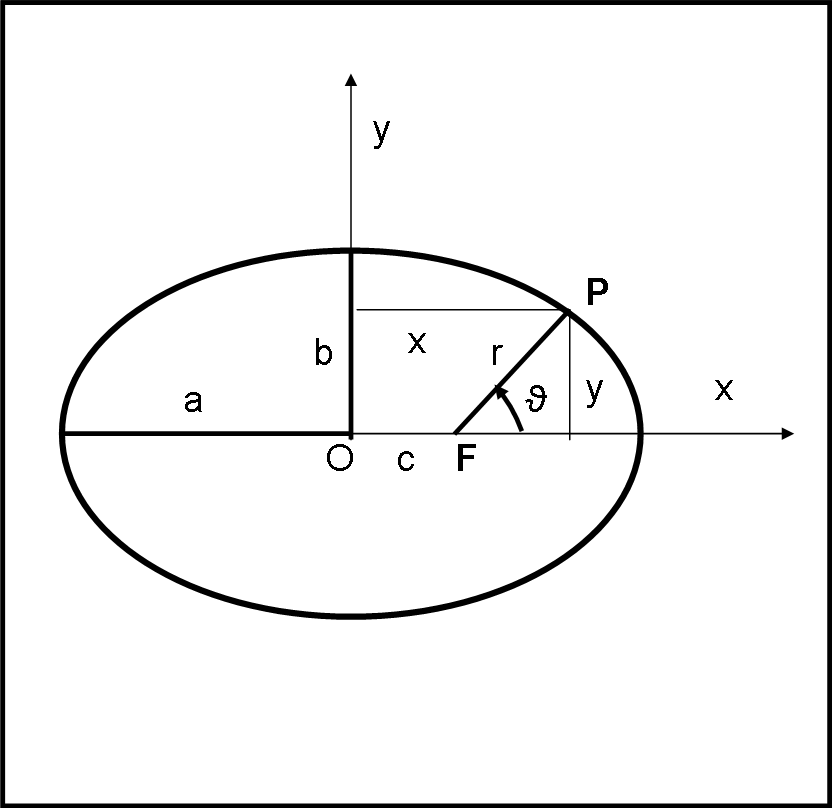
x²/a² + y²/b² = 1        …. (1)

Per questa formula e per la definizione di altri parametri potete andare QUI.

Spostando l’origine delle coordinate polari nel fuoco F, si ha:

x = c + r cos(ϑ)

y = r sin(ϑ)

Per cui, la (1) diventa:

(c² + r² cos²(ϑ) + 2rc cos(ϑ))/a² + r²sin²(ϑ)/b² = 1

b²c² + b²r²cos²(ϑ) + 2rcb²cos(ϑ) + a²r²sin²(ϑ) = a²b²

sappiamo, però, che sin²(ϑ) = 1 - cos²(ϑ), dato che:

sin²(ϑ) + cos²(ϑ) = 1

e, quindi:

b²c² + b²r²cos²(ϑ) + 2rcb²cos(ϑ) + a²r² - a²r²cos²(ϑ) = a²b²

Scriviamo c e b in funzione dell’eccentricità “e” e del semiasse maggiore a:

b = a(1 - e²)^1/2

c = ae

(1- e²)a⁴e² + a²(1- e²) r²cos²(ϑ) + 2rea³(1- e²) cos(ϑ) + a²r² - a²r²cos²(ϑ) = a⁴(1-e²)

dividiamo per a²

(1- e²)a²e² + (1- e²)r²cos²(ϑ) + 2rae(1- e²)cos(ϑ) + r² - r²cos²(ϑ) = a²(1- e²)

a²e² - a²e⁴ + r²cos²(ϑ) - e²r²cos²(ϑ) + 2raecos(ϑ) - 2rae³cos(ϑ) + r² - r²cos²(ϑ) = a² – a²e²

semplifichiamo i termini uguali e di segno opposto e raccogliamo quelli uguali:

2a²e² - a²e⁴ - e² r²cos²(ϑ) + 2raecos(ϑ) - 2rae³cos(ϑ) + r² - a² = 0

Cambiamo di segno e spostiamo qualche termine:

- 2a²e² + a²e⁴ + a² + e²r²cos²(ϑ)  - 2raecos(ϑ) + 2rae³cos(ϑ) = r²

Lavoriamo sui primi tre termini, mettendo in evidenza a²

a²(- 2e² + e⁴ +1) + e²r²cos²(ϑ)  - 2raecos(ϑ) + 2rae³cos(ϑ) = r²

a² moltiplica un trinomio che non è altro che il quadrato di (1 - e²)

a²(1 - e²)² + e²r²cos²(ϑ)  - 2raecos(ϑ) + 2rae³cos(ϑ) = r²

Mettiamo in evidenza 2raecos(ϑ) negli ultimi due termini del primo membro:

a²(1 - e²)² + e²r²cos²(ϑ) - 2rae(1 - e²)cos(ϑ) = r²

 Attenzione al primo membro! Non è altro che un quadrato.

Sostituendo, abbiamo:

(ercos(ϑ) - a(1-e²))² = r²

r = +/- (ercos(ϑ) - a(1-e²))          …. (2)

Quale segno dobbiamo prendere?

Sappiamo che r deve essere positivo. Consideriamo il caso particolare in cui e = 0. La (2) diventa:

r = +/- (-a)

a è, ovviamente, una quantità positiva, per cui, per ottenere una r positiva, dobbiamo prendere il segno meno. E questo deve valere anche nel caso generale, perciò:

r = - (ercos(ϑ) - a(1-e²))

r =  a(1- e²) - ercos(ϑ)

r(1 + ecos(ϑ)) = a(1- e²)

r = a(1- e²)/(1 + e cos(ϑ))    …. (3)

La (3) descrive un’ellisse in coordinate polari, riferita a un fuoco, al variare dell’angolo ϑ.

Il che vuole anche dire che un pianeta che orbita attorno al Sole deve descrivere l’ellisse (3), in cui a è il semiasse orbitale, “e” l’eccentricità, r la distanza del pianeta dal Sole e ϑ l’anomalia vera.

Questa non è altro che la prima legge di Keplero e quindi si dovrà arrivare a questo risultato partendo dalla legge di Newton.

Equazioni differenziali

Si fa in fretta a definire cos’è un’equazione differenziale: un’equazione che contiene le derivate di una variabile.

Qualcosa del tipo:

k d²y/dx² + h dy/dx + m y = n

L’equazione precedente descrive un’equazione differenziale del secondo ordine, lineare a coefficienti costanti. Ovviamente, si possono avere equazioni molto più complicate. Quella che abbiamo considerato, però, ci introduce al nostro problema di fondo.

Immaginiamo che y sia la posizione s di un punto e x sia il tempo t. L’equazione diventa:

k d²s/dt² + h ds/dt + m s = n

In questo caso, sappiamo molto bene cosa rappresentano le derivate: quella seconda è l’accelerazione e la prima è la velocità. Essa è un’equazione differenziale che descrive il moto di un oggetto. La soluzione, che necessita di integrali dovendo passare dalle derivate alla s, in funzione di t, descrive la legge oraria.

Facciamo due casi ancora più semplici per meglio inquadrare il concetto:

Poniamo che a (accelerazione) sia costante, si ha subito una prima equazione differenziale:

a  = dv/dt

dv = adt

Integrando ambo i membri, il primo tra v₀ e v e il secondo tra t₀ e t, si ha (vedi QUI):

∫_v0^v(dv) = ∫_t0^t (adt) = a ∫_t0^t dt

v  - v₀ = at - at₀

Ponendo t₀ = 0 si ha:

v  = v₀ + at

Che esprime la legge oraria della velocità in un moto uniformemente accelerato

La seconda equazione differenziale che prendiamo in considerazione è la seguente:

v = ds/dt

da cui:

ds = vdt

Ma conosciamo già il valore di v, dato da:

v = v₀ + at

Sostituiamo e otteniamo:

ds = (v₀ + at)dt

Possiamo integrare entrambi i membri

∫_s0^s(ds) = v₀∫_t0^t dt + a ∫_t0^t t dt

s – s₀ = v₀(t – t₀) + ½ a (t²-t₀²)

Ponendo t₀ = 0, si ha, infine:

s = s₀ + v₀t + ½ at²

che è la ben nota legge oraria del moto uniformemente accelerato.

Come già detto, però, le equazioni differenziali del moto possono essere ben più complicate e la prima legge di Keplero è proprio uno di quei casi… Noi, comunque cercheremo di arrivarci il più vicino possibile.

L'orbita è descritta su un piano

Dedichiamoci al problema più “difficile”, ossia a quello di ricavare il moto ellittico partendo dalla leggi di Newton. Ci accorgeremo che prima di arrivare alla fine, incontreremo già la seconda legge di Keplero, oltre che fare amicizia con un piano. In questa prima parte ci fermeremo proprio su questo piano. Procediamo con molta lentezza e chiarezza. Alla fine il moto orbitale avrà ben pochi segreti...

I vari passaggi che troveremo non sono assolutamente complicati, ma sono un ottimo esercizio di meccanica e di matematica. Non spaventatevi delle formule (in fondo sono solo frasi dette in una lingua meno conosciuta dell’italiano) e cerchiamo di andare avanti con molta calma, spiegando debitamente tutti i passaggi .

Si potrebbero scrivere libri interi su questo argomento (ed è anche stato fatto), ma noi cercheremo di estrarre i risultati fondamentali, quelli che meglio caratterizzano il moto di un pianeta.

Già partiremo con un qualcosa che ben raramente si tiene in conto e che si dà sempre per buono: la traiettoria di un pianeta (ellisse o cerchio o quello che sia) giace su un piano. L’istinto farebbe dire: “E’ ovvio!”, ma, prima dell’istinto, la matematica preferisce delle prove più decisive.

Il problema, che parte con la legge di gravitazione universale, è gioco forza un problema nelle tre dimensioni x, y e z. Sarebbe una bella scocciatura dover sempre lavorare nello spazio, sia per le figure relative che per i calcoli decisamente pesanti. Sarebbe molto bello togliersi subito il peso dello stomaco e dimostrare che il moto, qualsiasi esso sia, avviene su un piano. In tal modo, potremmo prendere questo piano come quello di riferimento e limitarci a due sole coordinate x e y.

Un bel vantaggio, ve lo assicuro, oltre al fatto che avremmo già un primo risultato che è nascosto nelle leggi di Keplero: l’orbita di un pianeta attorno al Sole avviene su un piano!

Cominciamo a disegnare la Fig. 4 che ci mostra un vettore nello spazio a tre dimensioni.

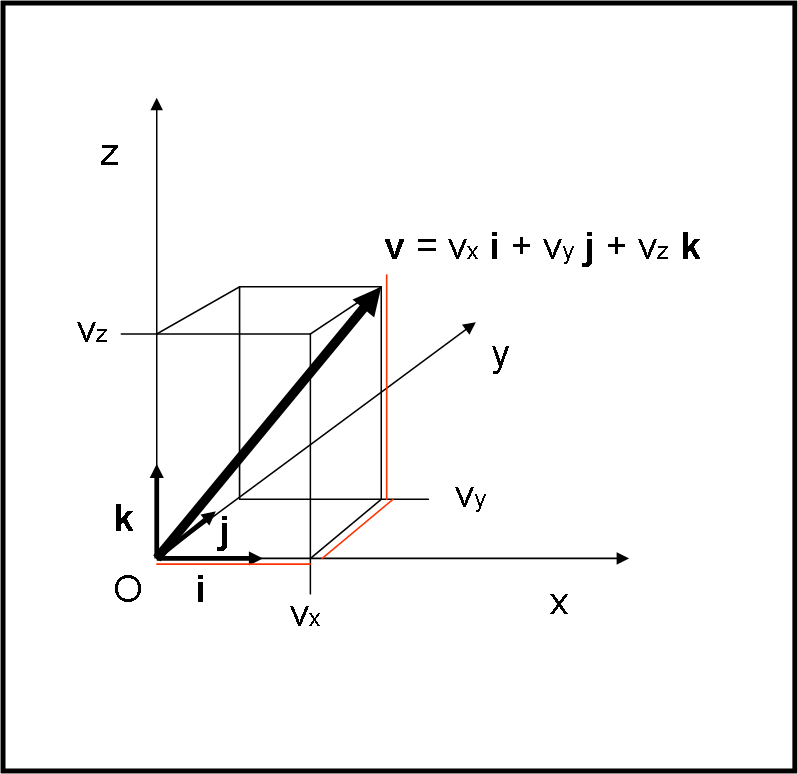
Come ben sappiamo (QUI) esso può essere descritto attraverso i versori i, j, k (relativi a x,y e z) e alle relative componenti. In parole matematiche:

v = v_xi + v_yj + v_z k

Questa è ovviamente una somma vettoriale e si nota facilmente che possiamo sommare prima i primi due vettori e poi, al loro vettore somma, sommare l’ultimo vettore.

Dobbiamo introdurre un primo dato di fatto che non possiamo dimostrare adesso, in quanto vorrebbe dire affrontare la geometria analitica a tre dimensioni. Argomento questo che sta trattando Arturo (QUI e seguenti). Tuttavia, ciò che stiamo per dire è abbastanza intuitivo.

Ricordiamo qual è l’equazione di una retta nel piano. Noi solitamente l’abbiamo scritta nella forma:

y = mx + n, ossia nella forma y = f(x).

Niente ci vieta, però, di scriverla in modo ancora più generico come:

ax + by + c = 0             …. (4)

Essa corrisponde a F(x,y) = 0 , ma dice esattamente la stessa cosa. Infatti, partendo da (1) si ha:

by = - ax – c

y = - ax/b - c/b = mx + n

Le due espressioni coincidono ponendo m = -a/b  e  n = - c/b.

Avevamo già fatto qualcosa di simile per l’ellisse e per il  cerchio (QUI), scrivendo l’equazione :

x²/a² + y²/b² = 1

Che non è altri che:

b²x² + a²y² = a²b²

ossia

Ax² + By² + F = 0

Essa è un caso particolare di una conica completa:

Ax² + By² + Cxy + Dx + Ey  + F = 0

Torniamo, comunque, alla nostra retta nel piano che ha equazione generale:

ax + by + c = 0

Una retta che passa per l’origine deve essere:

ax + by = 0

ossia y = (-a/b)x = mx

Quale sarà l’equazione di un piano nello spazio? Credetemi sulla parola:

ax + by + cz + d = 0

Questa funzione F(x,y,z) = 0 contiene tutti i punti che stanno su un piano comunque orientato nello spazio.

Se il piano passa per l’origine deve essere:

ax + by + cz = 0   (per O(0,0,0) si ha proprio 0)

in modo analogo alla retta.

E si apre un nuovo mondo. Sapete qual è l’equazione di una retta nello spazio? Estremamente complicata, ma anche ovvia: l’intersezione tra due piani non paralleli tra loro, ossia, il sistema:

ax + by + cz + d = 0

a’x + b’y + c’z + d’ = 0

Infatti, due piani non paralleli si tagliano secondo una retta e quindi i punti della retta intersezione devono soddisfare entrambe le equazioni dei due piani. Fermiamoci qui, se no cominceremmo a volare nelle tre dimensioni…

Prendiamo per buono perciò che l’equazione di un piano che passa per l’origine deve essere del tipo:

ax + by + cz = 0         …. (5)

Teniamola da parte, ricordandocela molto bene…

A questo punto, poniamo l’origine degli assi cartesiani in un punto qualsiasi O. Il Sole avrà coordinate x₀, y₀, z₀ e il pianeta P coordinate x, y, z. L’importante è che il baricentro del sistema Sole-Pianeta si muova rispetto a questi assi di moto rettilineo uniforme, in modo che non vi siano accelerazioni tra i due sistemi: l'importante e che il sistema Sole-Terra subisca solo le accelerazioni reciproche, ma non dipendenti dal moto del baricentro rispetto a un sistema esterno.... Stiamo facendo i raffinati, evitando di metterci direttamente nel Sole, ma c’è una ragione di generalità, che non può essere trascurata.  Il succo è che alla fine, facendo le differenze delle coordinate della posizione del pianeta e di quella del Sole, otterremo comunque le loro posizioni relative. Consideriamo la Fig. 5, in cui, per non complicare troppo la situazione, abbiamo solo disegnato il piano (x,y).

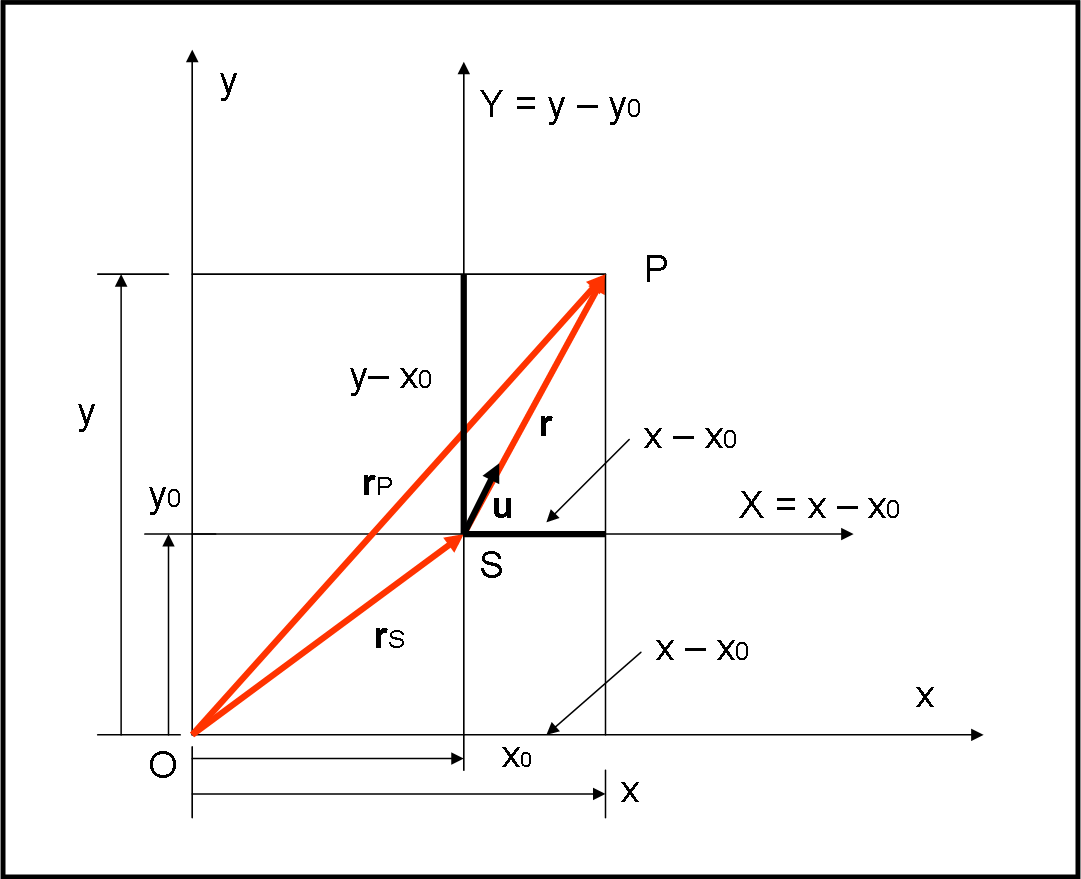
La stessa cosa vale, comunque, estendendo la figura alle tre dimensioni, ossia a ciò che abbiamo visto nella Fig. 4. Potremmo anche disegnare tre figure, ognuna per uno dei tre piani (x,y), (x,z) e (y,z), ma basta e avanza vedere come si opera in un solo piano. Le formule dovranno ripetere pari pari ciò che troviamo nel piano (x,y), cambiando le coordinate in modo corrispondente.

Cosa ci dice Newton? Abbiamo una massa M (Sole) e una massa più piccola m (pianeta) che vengono attratte reciprocamente dalla legge di gravitazione universale che vale, in valore assoluto:

F = G Mm/r²

Dove r è la distanza SP. Una formula che è bene trasformare in forma vettoriale, per poi calcolarne le componenti secondo gli assi.

A noi, infatti, interessa affrontare il problema nelle tre dimensioni e dobbiamo fare intervenire  le componenti dei vettori. Facciamo in fretta a mettere le cose a posto. r è ovviamente la congiungente S con P, ossia indica la posizione di P rispetto a S. In altre parole, possiamo esprimere r come vettore, utilizzando il suo modulo r e il versore unitario u lungo la direzione SP:

r = ru

 Moltiplicando il numeratore e il denominatore per r si ottiene la formula di Newton vettoriale:

F = GMmru/r³ = GMmr/r³

Non arrabbiatevi per questo passaggio che sembrerebbe inutile… ma per correttezza dobbiamo trovare le componenti del vettore e non lavorare solo con il modulo della forza.  Sono apparenti piccolezze, ma la Meccanica Celeste è severissima!

Tuttavia, vale anche, per il secondo principio della dinamica, F = ma. Il pianeta è attratto dal Sole con un’accelerazione a_P, mentre il Sole è attratto dal pianeta con accelerazione a_S

Otteniamo:

ma_P = - GMmr/r³

ma anche

Ma_S = GMmr/r³

a_P e a_S sono anche le derivate seconde della posizione di S e di P rispetto al tempo, nel sistema di origine O. Esse non sono certo uguali dato che una è quella che agisce su un corpo di massa m e l’altra su un corpo di massa M; è uguale invece il loro prodotto per la relativa massa, dato che non è altro che la legge di gravitazione.

Si ha, per il pianeta:

m d²r_P/dt² = - GMmr/r³

Il segno meno deriva dal fatto che r va dal Sole verso il pianeta, mentre r_P va in verso opposto.

Notate come abbiamo già introdotto un’equazione differenziale vettoriale? Prima o poi dovremo affrontarle di punta.

Per adesso consideriamo le tre componenti rispetto agli assi x, y e z.

md²x/dt² = - GMm(x - x₀)/r³

md²y/dt² = - GMm(y - y₀)/r³                …. (6)

md₂z/dt² = - GMm(z - z₀)/r³

Mentre per il Sole, abbiamo =

M d²r_S/dt² = GMmr/r³

ossia:

M d²x₀/dt² =  GMm(x - x₀)/r³

M d²y₀/dt² =  GMm(y - y₀)/r³                 …. (7)

M d²z₀/dt² =  GMm(z - z₀)/r³

Il segno vale adesso “più” dato che i vettori sono concordi

Per non riempire di formule l’articolo, svolgiamo il calcolo solo per la x. Una cosa del tutto analoga si ottiene anche per la y e la z.

Consideriamo la prima delle (6) e dividiamola per m. Abbiamo:

d²x/dt² = - GMm(x - x₀)/mr³ = - GM(x - x₀)/r³            …. (8)

Prendiamo la prima delle (7) e dividiamola per M. Otteniamo:

d²x₀/dt² =  Gm(x - x₀)/r³            …. (9)

Sottraiamo la (9) dalla (8) e abbiamo:

d²x/dt² - d²x₀/dt² = - GM(x - x₀)/r³ - Gm(x - x₀)/r³

d²x/dt² - d²x₀/dt² = - G(M + m)(x - x₀)/r³          …. (10)

Facciamo qualche semplificazione.

Chiamiamo x – x₀ = X    (vedi Fig. 5)

Ricordando che la somma delle derivate è uguale alla derivata della somma, si ha anche:

d²x/dt² - d²x₀/dt² = d²(x – x₀)/dt² = d²X/dt²

Poniamo, inoltre, per semplicità e dato che è una costante per il sistema:

μ = G(M + m)

La (7) diventa:

d²X/dt² = - μX/r³              …. (11)

Agendo in modo analogo per la y e la z, otteniamo:

d²X/dt² = - μX/r³

d²Y/dt² = - μY/r³             …. (12)

d²Z/dt² = - μZ/r³

O, ancora:

d²X/dt² + μX/r³ = 0

d²Y/dt² + μY/r³ = 0          …. (13)

d²Z/dt² + μZ/r³ = 0

Le (13) sono le equazioni (differenziali) del moto del pianeta rispetto al Sole. Pasticciamole ancora un po’…

Moltiplichiamo la seconda per Z e l’ultima per Y e poi sottraiamo membro a membro:

Z d²Y/dt² + ZμY/r³ - Yd²Z/dt² - YμZ/r³ = 0

Z d²Y/dt²  - Yd²Z/dt² = 0              …. (14)

Moltiplichiamo la terza per X e la prima per Z e poi sottraiamo:

Xd²Z/dt² + XμZ/r³ - Zd²X/dt² - ZμX/r³  = 0

Xd²Z/dt² - Zd²X/dt² = 0               …. (15)

Moltiplichiamo la prima per Y e la seconda per X e poi sottraiamo:

Yd²X/dt² + YμX/r³ - Xd²Y/dt² - XμY/r³ = 0

Yd²X/dt² - Xd²Y/dt²= 0                …. (16)

Consideriamo la (14). Possiamo scriverla:

d(ZdY/dt – YdZ/dt)/dt = 0        …. (17)

Non ci credete? Proviamo a calcolare la derivata…

dZ/dt dY/dt + Zd²Y/dt² – dY/dt dZ/dt – Yd²Z/dt² = Zd²Y/dt² - Yd²Z/dt²

Come volevasi dimostrare…

Ma se vale la (17) vuol dire che

Z dY/dt -Y dZ/dt = L = costante       …. (18)

La stessa cosa capita per la (15) e la (16) che diventano:

XdZ/dt - ZdX/dt = N = costante        …. (19)

YdX/dt - XdY/dt = Q = costante        …. (20)

Ancora un piccolo sforzo… Moltiplichiamo la (18) per X, la (19) per Y e la (20) per Z e poi sommiamole:

XZ dY/dt - XY dZ/dt + YXdZ/dt - YZdX/dt + ZYdX/dt  - ZXdY/dt = LX + NY + QZ

0 = LX + NY + QZ

In conclusione:

LX + NY + QZ = 0

Ma questa è l’equazione di un piano che passa per l’origine degli assi, cioè per il Sole.  Il che vuol dire che il moto di un corpo (pianeta) soggetto all’attrazione gravitazionale di un altro corpo (Sole) avviene in un piano che passa per il corpo centrale (Sole).

Leggete questo articolo attentamente. Sembra dire delle cose ovvie e invece è di fondamentale importanza, dato che dimostra che le orbite planetarie giacciono su un piano che contiene il Sole. Pensate alla nostra eclittica.

E’ difficile trovare questa dimostrazione, di estrema eleganza stilistica, non solo sul web, ma anche in molti libri. La mia versione, leggermente modificata per essere alla portata di tutti coloro che non si spaventano di qualche passaggio algebrico,  è merito indiscusso del testo di Meccanica Celeste in cui ho studiato tanti anni fa, scritto nel 1953, da quel grande astronomo che è stato Williams M. Smart.

Calma e sangue freddo…

Con uno sforzo non molto maggiore, possiamo arrivare alla descrizione della traiettoria di un pianeta, con il vantaggio non certo trascurabile di potere, finalmente, lavorare su un piano!

Verso la prima legge passando per la seconda

Affrontiamo in modo analitico la prima legge di Keplero. Ci accorgeremo che per arrivarci dobbiamo passare attraverso la seconda che acquista non solo un significato fisico ben preciso, ma che ci dimostra che il fatto che l’orbita giace su un piano poteva ricavarsi in modo immediato. C'è tanta matematica, quindi forza e coraggio... ma ne vale la pena!

Possiamo continuare nel nostro esercizio riferendo tutto a un piano dato che abbiamo dimostrato che il moto avviene su un piano passante per il Sole. Consideriamo, perciò, la Fig. 6, dove nell’origine vi è il baricentro del Sole S e P rappresenta il baricentro del pianeta che descrive una certa traiettoria da determinare. Siano x e y le coordinate cartesiane di questo punto P.

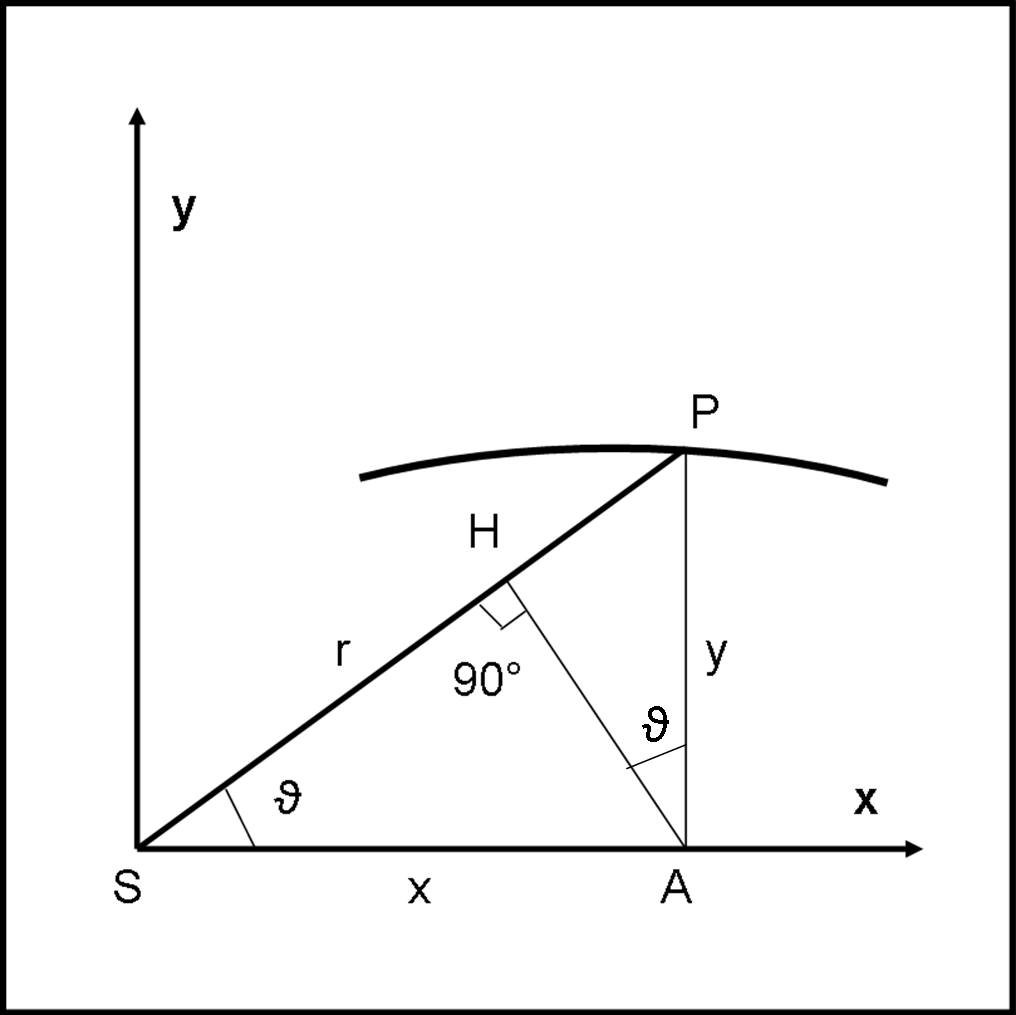
Possiamo immediatamente utilizzare le coordinate polari, dove SP = r:

r cos(ϑ) = x

r sin(ϑ) = y

E, una volta tracciata AH perpendicolare a SP,  dai triangoli rettangoli simili SHA e PHA (secondo teorema di Euclide) si ha che l'angolo HAP è uguale a ϑ, da cui:

r = SH + HP = x cos(ϑ) + y sin(ϑ)     …. (21)

Le equazioni del moto sono esattamente quelle definite nell’articolo precedente e date dalle (10), in cui consideriamo solo i due assi x e y.

d²x/dt² + μx/r³ = 0

d²y/dt² + μy/r³ = 0                …. (22)

Chiamiamo α e β le accelerazioni di P lungo la congiungente SP e lungo la sua perpendicolare.

α  è composto dalla somma di due termini che sono le due componenti dell’accelerazione d²x/dt²  e d²y/dt² lungo la congiungente SP. Deve, allora, essere:

α = d²x/dt² cos(ϑ) + d²y/dt² sin(ϑ)       …. (23)

Ripetiamo, per non confonderci, non abbiamo fatto altro che calcolare le componenti delle accelerazioni secondo x e y  lungo la congiungente SP.

Ricordando le (22) e sostituendo i valori di  d²x/dt²  e d²y/dt², abbiamo anche:

α = d²x/dt²  cos(ϑ) + d²y/dt² sin(ϑ) = - μx cos(ϑ)/r³ - μy sin(ϑ)/r³ = - μ/r³(x cos(ϑ) + y sin(ϑ))

la parentesi, però, non è altro che la (21) e, quindi:

α = - μr/r³ = - μ/r²

Possiamo scrivere:

α  = d²x/dt²  cos(ϑ) + d²y/dt² sin(ϑ) = - μ/r²           …. (24)

Calcoliamo, adesso β, somma delle componenti delle due derivate secondo la normale a SP.

Se l’angolo tra x e SP è uguale a ϑ, l’angolo tra x e la normale a SP deve essere (90 + ϑ) e quindi le componenti dell’accelerazione secondo la normale saranno date da (vedi QUI):

d²x/dt² cos(90 + ϑ) = - d²x/dt² sin(ϑ)

d²y/dt² sin(90 + ϑ) = d²y/dt² cos(ϑ)

Per cui β vale:

β = - d²x/dt² sin(ϑ) + d²y/dt² cos(ϑ) = μx/r³ sin(ϑ) - μy/r³ cos(ϑ) = (μ/r³)(x sin(ϑ) – y cos(ϑ))

Tuttavia, guardando la Fig. 6 si ha subito che

x sin (ϑ) = AH =  y cos(ϑ))

Ossia:

x sin(ϑ) – y cos(ϑ) = 0

E, di conseguenza:

β = - d²x/dt² sin(ϑ) + d²y/dt² cos(ϑ) = 0           …. (25)

Non dobbiamo certo stupirci di questo risultato, dato che l’accelerazione è solo radiale…

Non ci resta, adesso, che calcolare i valori di α e β, in coordinate polari, partendo dai valori di x e y. Finora abbiamo preso “per buone” le derivate seconde rispetto al tempo e abbiamo solo visto quanto valgono le componenti lungo SP e lungo la normale a SP.

Partiamo, direttamente, dalle:

x = r cos(ϑ)

y = r sin(ϑ)                …. (26)

Dobbiamo stare molto attenti a derivare, dato che sia r che θ sono funzioni del tempo.

Cominciamo con la prima delle (26), derivandola due volte rispetto al tempo:

dx/dt = cos(ϑ) dr/dt - r sin(ϑ) dϑ/dt

d²x/dt² = - sinϑ (dϑ/dt) (dr/dt) + cosϑ d²r/dt² - (dr/dt) sinϑ dϑ/dt - r cosϑ(dϑ/dt)²  - r sinϑ dϑ²/dt²

d²x/dt² = (d²r/dt²) cosϑ - 2 (dr/dt)(dϑ/dt) sinϑ– r (dϑ/dt)² cosϑ - r (d²ϑ/dt²) sin ϑ    …. (27)

Continuiamo con la seconda delle (26):

dy/dt = sinϑ dr/dt + r cosϑdϑ/dt

d²y/dt² = cosϑ (dϑ/dt) (dr/dt) + sinϑ d²r/dt² + (dr/dt) cosϑ dθ/dt – r sinϑ (dϑ/dt)²  + r cosϑ dϑ²/dt²

d²y/dt² = (d²r/dt²) sinϑ+ 2 (dr/dt)(dϑ/dt) cosϑ – r (dϑ/dt)² sinϑ+ r (dϑ²/dt²) cos ϑ    …. (28)

Dopo questa piccola fatica, andiamo a riprendere la (24):

α  = d²x/dt²  cos(ϑ) + d²y/dt² sin(ϑ) = - μ/r²

e inseriamo la (27) e (28)

α  = (d²r/dt²) cos²ϑ - 2 (dr/dt)(dϑ/dt) sinϑ cosϑ- r (dϑ/dt)² cos²ϑ  - r (dϑ ²/dt²) sinϑ  cos(ϑ) + (d²r/dt²) sin²ϑ + 2 (dr/dt)(dϑ/dt) sinϑ cosϑ - r (dϑ/dt)² sin²ϑ + r (dθ²/dt²) sinϑ cosϑ

Semplificando:

α  = (d²r/dt²) cos²ϑ- r (dθ/dt)² cos²ϑ + (d²r/dt²) sin²ϑ - r (dϑ/dt)² sin²ϑ

Raccogliendo:

α  = (d²r/dt²)(cos²ϑ + sin²ϑ ) - r (dθ/dt)² (cos²ϑ + sin²ϑ)

Ricordando che:

(cos²ϑ + sin²ϑ) = 1

Abbiamo, infine:

α  = (d²r/dt²) - r (dϑ/dt)² = - μ/r²          …. (29)

Analogamente, possiamo prendere la (25) e inserire al suo interno le (27) e (28)

β = - d²x/dt² sin(ϑ) + d²y/dt² cos(ϑ) = 0

β = - (d²r/dt²) sinϑ cosϑ + 2 (dr/dt)(dϑ/dt)sin²ϑ  + r (dϑ/dt)² sinϑ cosϑ+ r (dϑ²/dt²)sin²ϑ

+ (d²r/dt²)sinϑ cosϑ + 2 (dr/dt)(dϑ/dt) cos²ϑ – r (dϑ/dt)² sinϑ cosϑ  + r (dϑ²/dt²) cos²ϑ

E, infine:

β = + 2(dr/dt)(dϑ/dt) + r (dϑ²/dt²) = 0      …. (30)

Moltiplichiamo e dividiamo quest’ultima equazione per r:

(1/r) (2r(dr/dt)(dϑ/dt) + r²(dϑ²/dt²)) = 0     …. (31)

Ciò che moltiplica 1/r non è altro che la derivata rispetto al tempo di r²(dϑ/dt). Proviamolo…

d(r²(dϑ/dt))/dt = 2r (dr/dt) (dϑ/dt) + r²(dϑ²/dt²)

Ma, allora, la (31) può essere scritta:

(1/r) d(r²(dϑ/dt))/dt = 0

Per r diverso da infinito (altrimenti l’equazione darebbe zero qualsiasi sia il valore della derivata), si ha:

r²(dϑ/dt) = costante  = h            …. (32)

La seconda legge di Keplero

Quasi senza accorgercene abbiamo ricavato la seconda legge di Keplero. Soffermiamoci un poco su di lei e sul suo significato fisico. Poi proseguiremo verso la prima legge.

Quello che abbiamo scritto è qualcosa di estremamente importante. Dimostriamolo in modo un po’ approssimato, ma essenzialmente corretto. Consideriamo la Fig. 7.

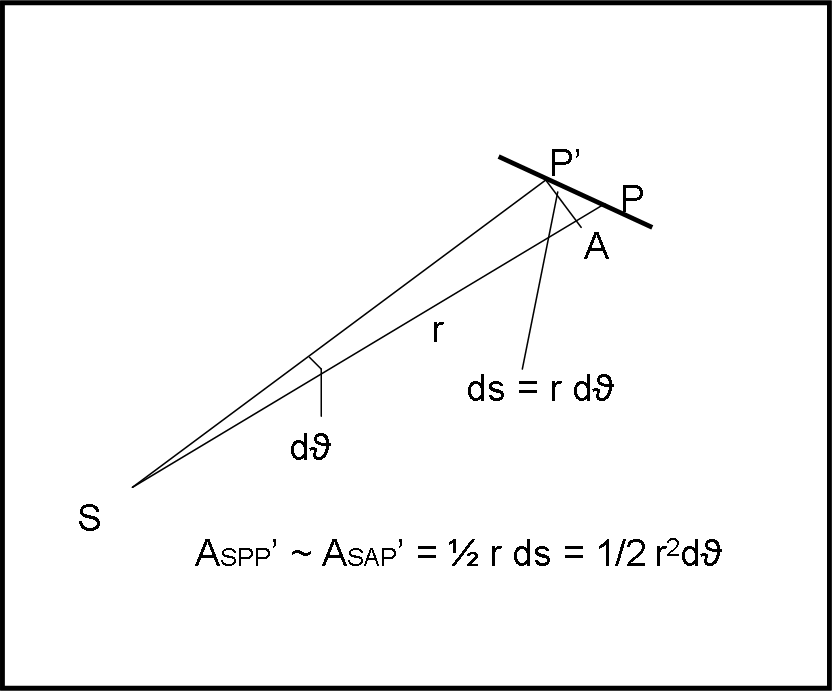
In un tempo dt molto piccolo il raggio vettore si sposta formando un angolo dϑ con il precedente. Se il tempo è infinitesimo possiamo considerare PP’ uguale ad AP’. L’area del triangolo SP’P può assumersi uguale a SAP’. Facendo tendere dt a zero, la faccenda si sistema anche matematicamente.

Quanto vale la sua area? Base per altezza diviso due. La base non è altro che r e l’altezza è ds = r dϑ (penso che non ci sia bisogno di spiegare questa formuletta, basta una proporzione…).

L’area è perciò ½ r ∙ r dϑ = ½ r²ϑ. Quest’area è funzione del tempo e possiamo calcolare come varia in funzione di questo, ossia possiamo calcolare la sua derivata che indica la velocità areolare descritta dal vettore r in un tempo dt. Essa è valida per qualsiasi  traiettoria e vale:

Velocità areolare = ½ r² dϑ/dt  = h/2  …. (33)

La (32) ci dice proprio che la (33) è una costante del moto, ossia descrive la seconda legge di Keplero.

Avrete sicuramente notato che l’espressione di β (da cui si ricava la seconda legge) indica praticamente che l’accelerazione normale al raggio vettore è uguale a zero. La costanza della velocità areolare è quindi una caratteristica dei moti in cui agisce una forza diretta verso il centro. Nel nostro caso questa forza è proprio quella di gravità.

Dimostriamo velocemente che il significato fisico di quanto detto è estremamente importante.

Il punto P viaggia con una velocità sempre tangente alla traiettoria. Calcoliamo il momento angolare, ossia il momento della quantità di moto.  Scomponiamo la velocità nelle sue due componenti: normale e radiale. Quella normale non è altro che r dϑ/dt. La velocità radiale v_r ci interessa poco e lasciamola pure nel vago. Infatti, eseguendo il prodotto vettoriale tra raggio vettore e componenti della velocità si ha che il modulo relativo alla componente radiale vale (α è l’angolo tra raggio vettore e componente della velocità):

L_R = m r v_r sinα = m r v_r sin(0) = 0

Il modulo del momento angolare è quindi solo quello dato dalla componente normale, ossia:

L = m r dϑ/dt r sin (90°) = mr²dϑ/dt     …. (34)

La (33), però, ci dice che:

½ r² dϑ/dt  = h/2

r² dϑ/dt  = h

Per cui la (34) diventa:

L = mr²dϑ/dt  = mh = costante

Per ricordare il momento angolare e il prodotto vettoriale potete andare  QUI (vi servirà anche dopo).

Ne consegue che la seconda legge di Keplero equivale a dire che il momento angolare di un corpo orbitante attorno al Sole è costante. Tanta fatica per così poco? In realtà ci si poteva arrivare subito… In altre parole, partendo dalla costanza del momento angolare si può arrivare velocemente alla seconda legge. Vale la pena dimostrarlo attraverso i vettori, in modo da richiamare il prodotto vettoriale ed eseguire un calcolo più … raffinato.

Potremmo partire con una semplice frase: dato che la forza è centrale, il suo momento deve essere ZERO e quindi deve essere costante il momento angolare. Ricordiamo ancora quanto si era detto e dimostrato QUI:  il momento angolare di un punto di massa m si conserva se è nullo il momento delle forze che agiscono su di lui. In questo caso l’unica forza agente è quella di gravità.

Vale la pena richiamare anche questa dimostrazione …

Sia L il momento angolare, F la forza e M il suo momento. Possiamo scrivere:

L =  r Λ mv

dL/dt = d(rΛ mv)/dt = (dr/dt) Λ mv + r Λ d(mv)/dt

Tuttavia, (dr/dt ) Λ mv = 0 (vettori paralleli). Se non ricordate perché, basta andare a vedere la Fig. 21 dell’articolo sul momento angolare (sempre quello di prima)...

dL/dt =  r Λ d(mv)/dt

Tuttavia, sappiamo molto bene che la derivata rispetto al tempo della quantità di moto non è altro che la forza F, per cui:

dL/dt = r Λ F = M

Ma, per definizione, r e F sono paralleli e quindi:

M = 0

In altre parole la derivata di L è uguale a ZERO e quindi L deve essere costante.

Procediamo, ricordando che cosa ci permette di calcolare il modulo del prodotto vettoriale: il modulo del prodotto vettoriale di due vettori v e u è uguale all'area del parallelogramma costruito sui due vettori.

(base per altezza, vedi Fig. 14 dell’articolo sul Momento Angolare). Ne segue che la metà di questa area è proprio quella del triangolo che vediamo nella Fig. 8

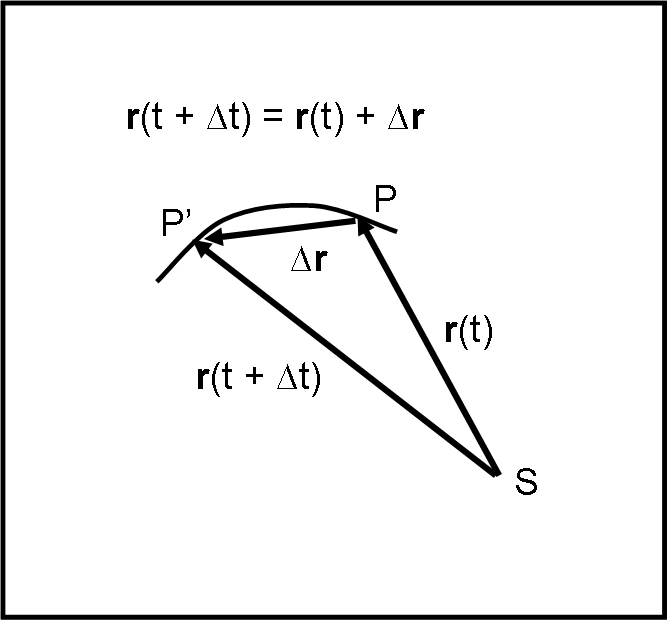
Questo triangolo ha come lati il vettore r = r(t) e il vettore r(t + ∆t) = r + ∆r . Possiamo considerare il vettore che unisce i loro vertici uguale alla curva PP'. L’approssimazione è più che valida, dato che facendo tendere ∆t a zero la curva coincide con il segmento.

Per quanto detto poco fa, la sua area vale, perciò:

∆A = ½ r Λ (r + ∆r)      …. (35)

r Λ r = 0

∆A = ½ r Λ ∆r

E la sua variazione con il tempo (la velocità areolare):

dA/dt = ½ lim _{∆t →0} ∆A/∆t = ½ lim _{∆t →0} (r Λ ∆r)/∆t = ½ r Λ lim _{∆t →0}(∆r/∆t) = ½ r Λ v

dA/dt = (r Λ v)/2

Ma sappiamo che:

L =  r Λ mv

r Λ v = L/m

Abbiamo appena dimostrato che L è costante e, quindi:

dA/dt = L/2m = costante

Nuovamente la seconda legge di Keplero

Come avete visto abbiamo agito con i vettori. Il fatto di aver trovato che il vettore momento angolare è costante vuole anche dire che la superficie in cui si svolge il moto deve essere un piano, dato che è l’unico modo per avere un vettore costante come modulo, direzione e verso.

In questo modo tutto si semplifica come calcoli, ma necessita di un’ottima conoscenza dei vettori e del momento angolare. Scegliete voi…

Tuttavia, per proseguire verso la prima legge di Keplero è meglio rifarsi ai calcoli analitici.

L'equazione differenziale fondamentale

Il nostro compito, adesso, è definire al meglio l’equazione differenziale da risolvere e non è cosa da poco.

Capisco che quanto svolto in questi ultimi articoli sembri molto impegnativo. In realtà non lo è, dato che abbiamo usato regole di cui dovremmo avere una discreta conoscenza. L’importante è affrontarle con la dovuta calma e attenzione. Le difficoltà sono state minime, ma, in compenso, siamo riusciti a dedurre la seconda legge di Keplero nel modo più generale possibile. E, credetemi, non è cosa da poco! Soprattutto abbiamo visto che essa non è altro che la conseguenza di una forza centrale che quindi non può far variare il momento angolare del sistema. Ed esso è dato, ovviamente, dal prodotto vettoriale tra velocità e distanza dal fuoco. Se cresce una deve decrescere l’altro e viceversa, ossia deve mantenersi costante l’area descritta dal raggio vettore nell’unità di tempo.

Bando alle ciance e andiamo dritti fino alla prima legge di Keplero, la parte più difficile, che ci obbliga a prendere per buona la soluzione di un’equazione differenziale. Per noi è, al momento, troppo impegnativa, ma chi vuole saperne di più trova un link adeguato.

Ripartiamo dalla (32)...

r²(dϑ/dt) = costante  = h            …. (36)

Affrontiamo il problema di determinare la traiettoria del corpo P attorno al fuoco S. In poche parole, cerchiamo di scrivere la legge oraria in coordinate polari. Per far ciò dobbiamo cercare di eliminare il tempo dalla nostra relazione e far comparire solo il raggio vettore e la sua variazione con l’angolo ϑ.

Cominciamo col porre, solo per convenienza nella futura integrazione:

u = 1/r

La (36) diventa:

(dϑ/dt) = hu²         …. (37)

L’equazione fondamentale è la (29) dove compaiono le derivate di  r e di ϑ rispetto al tempo.

α  = (d²r/dt²) - r (dθ/dt)² = - μ/r²

Dobbiamo trasformarla in un’equazione differenziale in cui le derivate del raggio siano solo funzione dell’angolo. Il succo di tutto è trasformare la (29) in un’equazione in cui compaiano solo le derivate di r (o di u) rispetto a ϑ. Per far questo dobbiamo mischiare un po’ le carte, ma in modo estremamente semplice.

Partendo dalla definizione di u = 1/r, ossia r = 1/u, deriviamo la r rispetto al tempo e vediamo se si riesce a far intervenire al suo posto la variabile ϑ.

Ricordiamo quanto vale la derivata di un quoziente e in particolare di 1/y (dy/dx = - (1/y2)dy/dt)

dr/dt = d(1/u)/dt = - (1/u²)du/dt

Ma:

du/dt = (du/dϑ)(dϑ/dt)

e, quindi:

dr/dt = - (1/u²) (du/dϑ)(dϑ/dt)

La (37), però, ci dice quanto vale dϑ/dt, ossia hu². Sostituendo nella relazione precedente, otteniamo:

dr/dt = - (1/u²) (du/dϑ) hu² = - h du/dϑ      …. (38)

Eseguendo una specie di semplice gioco di prestigio siamo riusciti a esprimere la derivata prima del raggio rispetto al tempo come una derivata del raggio (u non è altro che il suo inverso) rispetto all’angolo.

Eseguiamo adesso la derivata seconda di r rispetto al tempo:

d²r/dt² = d(dr/dt)/dt = (d(dr/dt)/dϑ)(dϑ/dt)

il solito trucchetto di moltiplicare sopra e sotto per dϑ

Ma la (38) ci permette di inserire il valore ottenuto per dr/dt e si ottiene:

d²r/dt² = (d/(dr/dt)/dϑ)(dϑ/dt) = (d(- h du/dϑ)/dϑ)(dϑ/dt) = - h (d²u/dϑ²)(dϑ/dt)

Abbiamo ancora un dϑ/dt che ci dà fastidio… Nessuna paura, basta ricordare la (37):

d²r/dt² = - h (d²u/dϑ²)(dϑ/dt) = - h (d²u/dϑ²)(hu²) = - h²u²(d²u/dϑ²)      …. (39)

Riscriviamo, per metterle bene in evidenza, le (38) e (39) che esprimono le derivate di r rispetto al tempo come derivate di u rispetto all’angolo ϑ.

dr/dt = - h du/dϑ

d²r/dt² = - h²u²(d²u/dϑ²)

Riscriviamo anche la (29) e vediamo se abbiamo bisogno d’altro…

(d²r/dt²) - r (dϑ/dt)² = - μ/r²             …. (40)

In realtà, ci manca ancora la dϑ/dt. Ma no! Ce lo dice la (37):

(dθ/dt) = hu²

Sostituiamo e abbiamo, infine:

- h²u²(d²u/dϑ²) - (1/u) (hu²)² = - μu²

h²(d²u/dϑ²) + h²u =  μ

d²u/dϑ²  + u = μ/ h²      …. (41)

Qualcuno potrebbe dire: “Tanta fatica per ottenere ancora un’equazione differenziale… chi ce l’ha fatto fare?”

In realtà la (41) è una “classica” equazione del secondo ordine di cui è possibile trovare una soluzione (attraverso gli integrali). Non è cosa tanto semplice, ma la soluzione analitica c’è, mentre non ci sarebbe stata se avessimo aggiunto un terzo corpo (non per niente il problema dei tre corpi non ha una soluzione analitica).

Anche se sembra impossibile, l’integrazione della (41) fa comparire un coseno dell’angolo ϑ più qualche costante d’integrazione che possiamo ricavare a posteriori…

La soluzione generale della (41) è:

u = μ/h² (1 + (A h²/μ) cos(ϑ - ϑ₀))        …. (42)

Dove A e ϑ₀ sono le due costanti di integrazione (abbiamo una derivata seconda e quindi si deve integrare due volte…).

N.B.: chi si vuole togliere il gusto di vedere come si risolve un’equazione differenziale di questo tipo può andare QUI , al Cap.7, sapendo, però, che incontrerà i numeri immaginari…

Per tutti gli altri, elaboriamo leggermente la formula precedente, ricordando che r = 1/u. Otteniamo:

r = (h²/μ)/((1 + A h²/μ) cos(ϑ - ϑ₀))       …. (43)

Questa è esattamente la (3) del primo articolo:

r = a(1 - e²)/(1 + e cos(ϑ))   

Dove:

h²/μ = a(1- e²)

A h²/μ = e

ϑ₀ = 0     (solitamente esso rappresenta il perielio)

Insomma, accettando per buona la soluzione dell’equazione differenziale, abbiamo dimostrato la prima legge di Keplero.

In particolare, se e = 0, abbiamo:

r = a      (cinconferenza)

Se e < 1     si ottiene un’ellisse

Se e = 1     si ottiene una parabola (non spaventatevi se vi sembra che il numeratore vada a zero. In realtà e = 1, ma a tende a ∞ e quindi il numeratore è una forma indeterminata).

Se e > 1    si ottiene un’iperbole.

Non è immediato vedere la differenza tra queste curve, ma, magari, in seguito…

La terza legge di  Keplero

Non ci resta che dedurre la terza legge di Keplero, quella forse più importante e usata. La deduciamo per un’orbita qualsiasi, ma è già ben noto (e immediato) il procedimento da usare nel caso di un’orbita circolare, che richiamiamo per semplicità.

Cominciamo, quindi, con il caso più semplice, ossia quello relativo a un’orbita circolare di raggio r. In realtà, per ottenerla, basta eguagliare la forza gravitazionale con la forza centrifuga, in modo da ottenere l’equilibrio per il corpo orbitante. Siano M e m le masse del Sole e del pianeta.

La legge di gravità dice:

F_G = G m M/r²

La forza centrifuga (QUI) è data da:

F_C = m ω² r

Dove ω è la velocità angolare che vale, ovviamente:

ω = 2π/P               (P = Periodo orbitale)

Uguagliando le due forze si ha:

G m M/r² =  m (4π²/P²) r

G M/r³ = 4π²/P²        …. (44)

Riscriviamo la terza legge di Keplero: “I quadrati dei periodi di rivoluzione dei pianeti sono proporzionali ai cubi dei semiassi maggiori delle loro orbite”. Nel caso di orbite circolari si può sostituire semiasse con raggio e quindi la formulazione matematica della legge diventa:

r³/P² = costante

Ma la (44) può scriversi:

r³/P² = GM/4π² = costante

Che è proprio la terza legge di Keplero.

Passiamo adesso al caso di un’orbita ellittica. La faccenda non è certo molto complicata. Basta ricordarsi (che:

h²/μ = a(1- e²)          ….   (45)

Ma h è il doppio della velocità areolare (costante).

La velocità areolare è l’area descritta nell’unità di tempo, per cui possiamo facilmente estrapolarla a tutta l’ellisse:

h = 2 (Area ellisse/tempo impiegato a percorrerla) = 2 π ab/P

h = 2 π a a(1 – e²)^1/2/P = 2 π a² (1 – e²)^1/2)/P

Scriviamo il valore di h²/μ, sostituendo h trovato sopra

h²/μ = (2 π a² (1 – e²)^1/2)/P)²/μ = (4 π² a⁴ (1 – e²))/P²)/μ

Applicando la (45):

(4 π² a⁴ (1 – e²))/P²)/μ = a (1 – e²)

Semplificando:

4 π² a⁴/P² = μ a

4 π² a³/P² = μ

Ma:

μ = G(M + m)  = costante

E, infine:

a³/P² = G(M + m)/ 4 π² = costante

Questa è nuovamente la terza legge di Keplero. In particolare, essa è quella più esatta, in quanto tiene anche conto della massa del pianeta m, che per quanto piccola rispetto a quella del Sole M, non può essere trascurabile per la maggior parte dei calcoli di meccanica celeste, anche elementare.

Il moto dei due corpi non si esaurisce certo così, ma, almeno per il momento, abbiamo ottenuto quello che volevamo, ossia ricavare le tre leggi di Keplero partendo dalla legge di gravitazione universale di Newton.

 

QUI un'appendice dedicata alla velocità orbitale di un oggetto nel caso generale dell’ellisse

Se siete curiosi di sapere come è riuscito Richard Feynman ad ottenere lo stesso risultato solo giocando su triangoli uguali e su un diagramma geniale, potete leggere QUI

Cosa c'entra il grande genio greco Aristarco con la terza legge di Keplero? Scopritelo QUI

Mela o non mela… questo è il problema! QUI  una semplice e divertente spiegazione di Curiuss, coadiuvato dal fido assistente micio Gualtiero, sulla genialità dell’intuizione di Newton circa la Legge di Gravitazione Universale.