Obiettivo di questo articolo, di cui viene pubblicata ora la prima parte, è quello di entrare nell'affascinante mondo della geometria dello spazio. Dopo la seconda parte, facendo uso della geometria solida, verrà dimostrato che, come spiegato nei commenti al quiz che trovate QUI, la curva congiungente due punti situati su una superficie sferica e che misuri la minore distanza tra essi è un arco di circonferenza massima, ossia avente centro coincidente con quello della sfera. Per introdurci nella geometria dello spazio, vengono richiamati alcuni concetti di geometria piana, già trattati nella sezione "Viva la Matematica" degli Approfondimenti, ad esempio QUI.

 

Punti e rette nel piano

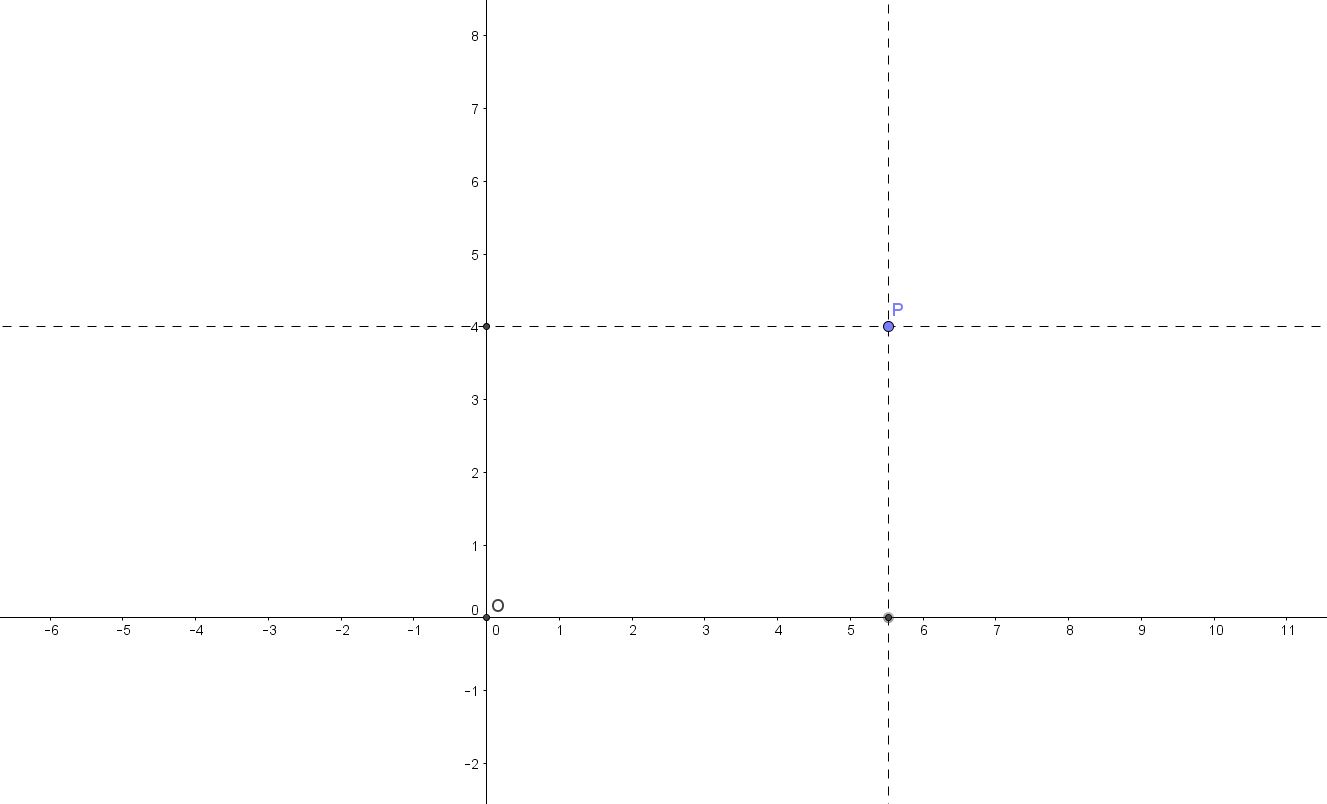
Tutti noi sappiamo disegnare su un foglio di carta un punto o una linea retta. Se consideriamo il foglio di carta come piano di riferimento, sul quale fissiamo un sistema di due assi (x ed y), per esempio tra loro ortogonali, chiamati assi cartesiani e che si intersecano in un punto che chiamiamo origine degli assi, allora possiamo attribuire ad un punto disegnato sul foglio una coppia di coordinate, chiamate ascissa (sull’asse x) ed ordinata (sull’asse y), che individua in modo univoco  la posizione del punto sul foglio. Stabiliamo in questo modo quella che si definisce “corrispondenza biunivoca” tra punti del  piano e loro coordinate cartesiane. La corrispondenza biunivoca garantisce che ad un punto nel piano corrisponde una ed una sola coppia di coordinate (x, y) , e viceversa. Nella figura 1, ad esempio, la coppia di coordinate (11/2 , 4) determina  la posizione del punto P nel sistema di riferimento xOy. Se, invece, partissimo disegnando prima il punto P, allora mediante il sistema di riferimento adottato, troveremmo in corrispondenza di P l’unica coppia di coordinate  (11/2 , 4) ad esso relativa.

Se ora sul suddetto foglio di carta disegniamo due punti , unendoli e proseguendo, aiutandoci con un righello, da entrambe le parti in linea retta, otteniamo la retta passante per i due punti dati (figura 2) . Un tratto di retta tra due punti, nel piano, è la linea più corta che unisce i due punti. Non esiste un’altra linea che unisca i due punti e sia più corta del tratto di retta che li congiunge. Anche la retta, nel piano, viene univocamente individuata dalla sua equazione cartesiana. Questa si può ottenere introducendo il concetto di luogo geometrico. Cosa è un luogo geometrico ? E’ semplicemente l’insieme dei punti, in questo caso del piano, che godono di una particolare proprietà geometrica. Chiediamoci, dunque: quale è la proprietà geometrica di cui godono tutti i punti di una retta nel piano ? Consideriamo tre punti su una retta, A di coordinate (xa, ya), P di coordinate (x, y),  B di coordinate (xb, yb).

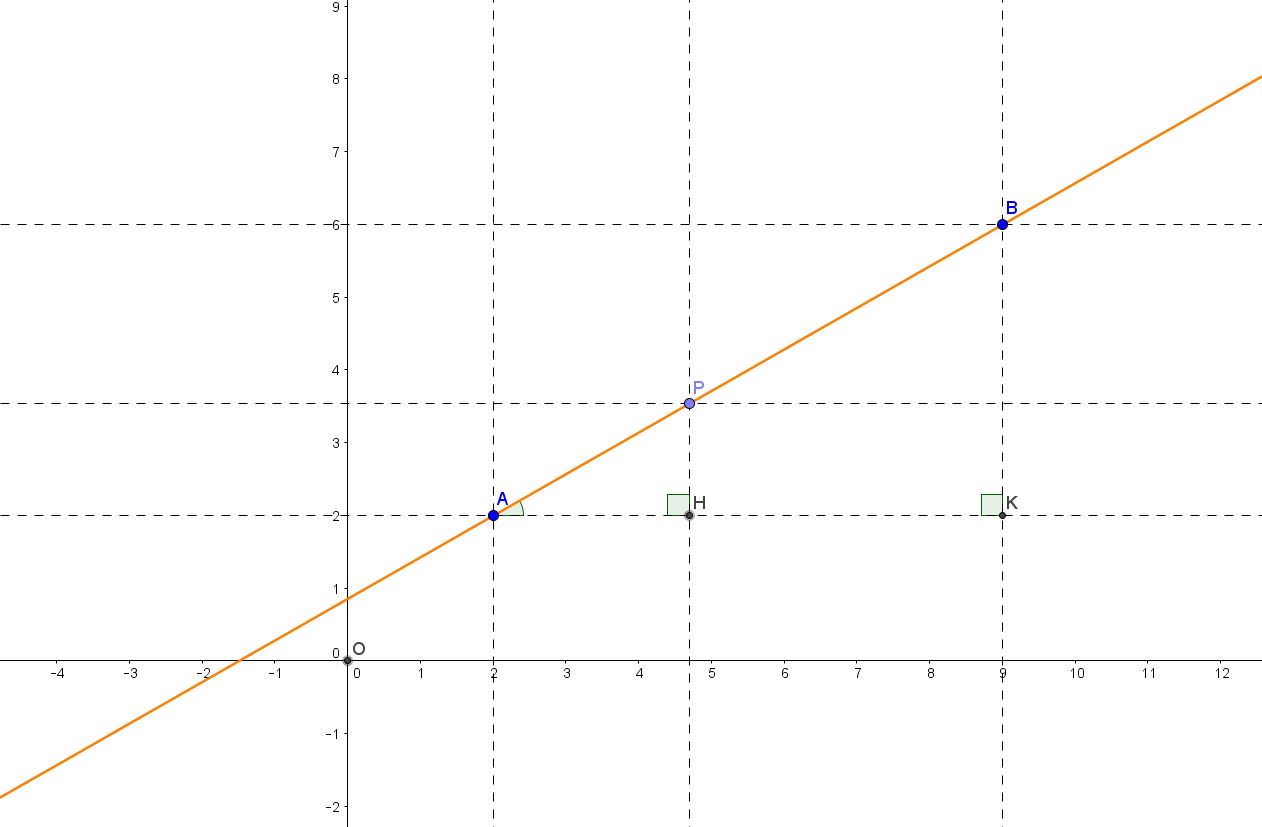
I triangoli AHP e AKB sono rettangoli, rispettivamente in H e K. Infatti, con riferimento al triangolo AHP, il lato PH è parallelo all’asse y , il lato AH è parallelo all’asse x e gli assi x e y sono tra loro perpendicolari per costruzione. Quindi i lati PH e AH devono essere tra loro perpendicolari. Così anche per il triangolo AKB. Inoltre, i due triangoli sono tra loro simili. Infatti , l’angolo KAB è uguale, anzi è proprio coincidente, con l’angolo HAP e l’angolo AKB è uguale all’angolo AHP perché entrambi di 90 gradi. Per il primo criterio di similitudine dei triangoli, quindi, i due triangoli in questione sono simili. Se sono simili , posso allora scrivere la relazione:

BK : PH = AK : AH

che posso anche scrivere come

BK : AK = PH : AH            (1)

Questa relazione ci dice che è costante, su una retta, il rapporto tra la differenza delle ordinate e la differenza delle ascisse di una qualsiasi coppia di suoi punti. Possiamo , dunque, dire che la retta è il luogo geometrico dei punti del piano che godono della suddetta proprietà. Ricaviamo da questa considerazione l’equazione della retta nel piano. Basta sostituire nella (1) le lunghezze dei lati che otteniamo dalla figura:

Quindi la (1) diventa:

cioè:

Svolgendo i calcoli, portando tutto a primo membro e ordinando, otteniamo:

              (2)

Se ora poniamo:

possiamo scrivere la (2) come:

ax+by+c=0                   (3)

Questa è dunque l’equazione, detta in forma implicita, della retta nel piano. E’ anche possibile scriverla in forma esplicita , cioè esplicitandola rispetto alla y:

e ponendo

otteniamo:

y=mx+q                       (4)

che è appunto l’equazione in forma esplicita della retta nel piano.

Se in tale equazione poniamo x=0, otteniamo y=q. Porre x=0 nell’equazione di una retta significa ricavare l’ordinata del punto appartenente alla retta e avente ascissa nulla. Ma un punto avente ascissa nulla appartiene necessariamente anche all’asse y (la cui equazione cartesiana è proprio x=0). Porre x=0 , quindi, significa in pratica, trovare il punto di intersezione tra la retta e l’asse y. Tale punto ha coordinate (0, q). Il termine q si definisce intercetta. Cosa rappresenta, invece, il termine m ? Lo avevamo definito come

ossia, rammentando la definizione di a e di b:

cioè, con riferimento sempre alla figura 2,

m, quindi, è il rapporto tra la differenza di ordinate e la differenza di ascisse di due qualsiasi punti della retta e, per come è stata definita la retta come luogo geometrico, è costante. Esso si definisce coefficiente angolare della retta.

 

Punti e rette nello spazio

Cosa succede ora se aggiungiamo la terza dimensione , cioè se ci spostiamo dal foglio di carta allo spazio tridimensionale ?

Per quanto riguarda i punti, il discorso è molto semplice. Ciascun punto dello spazio sarà univocamente individuato non più da una coppia ma da una terna di coordinate cartesiane, (x, y, z). Anche nello spazio possiamo stabilire una corrispondenza biunivoca tra punti e terne di coordinate cartesiane.

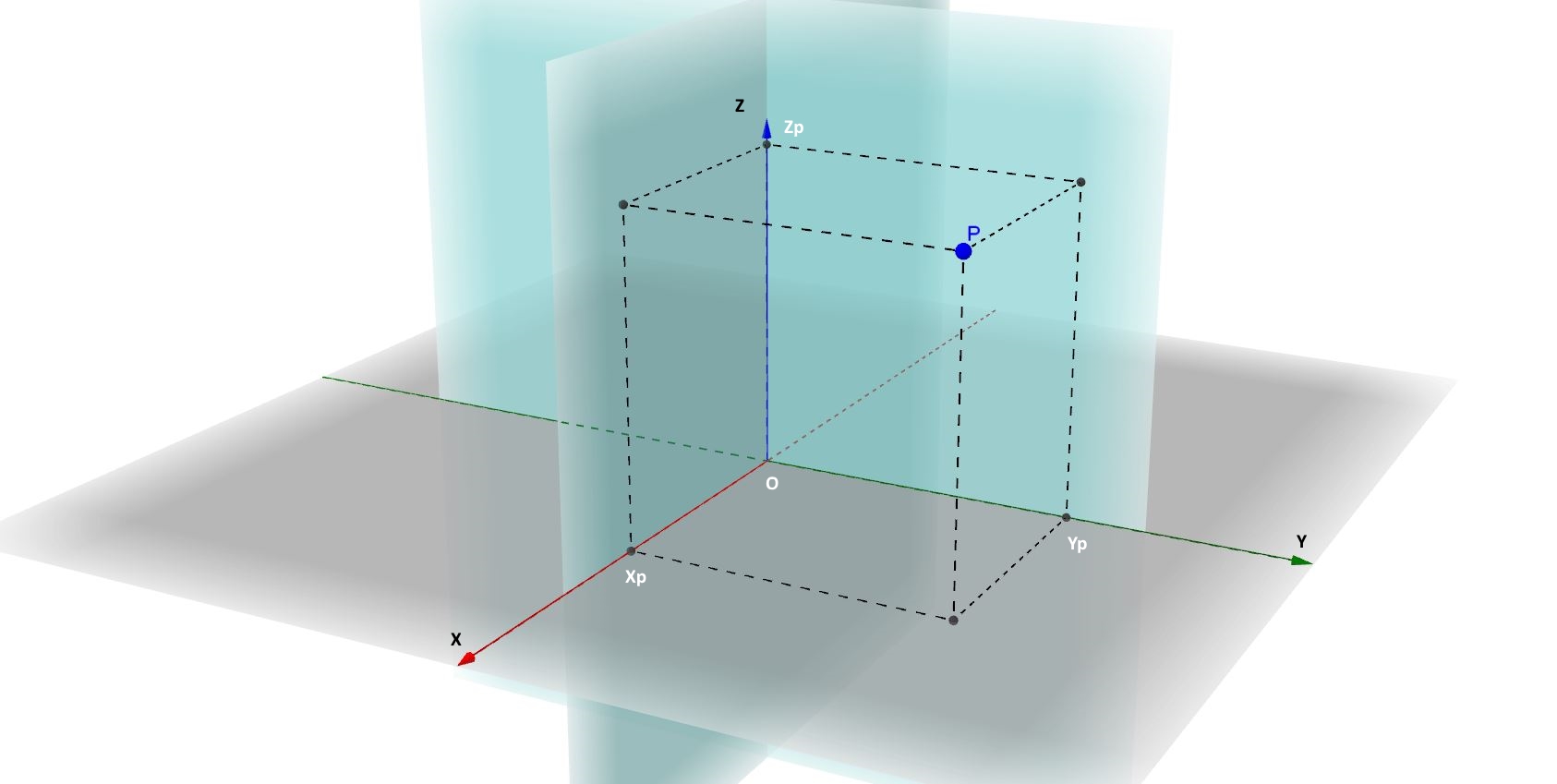
E per la retta ?

Nello spazio i punti di una retta continuano a godere della proprietà vista nel caso del piano, ma il discorso andrebbe fatto secondo due direzioni, perché ciascun punto di una retta nello spazio ha tre coordinate e non due. Con riferimento alla figura 4, il ragionamento fatto nel caso del piano, andrebbe ripetuto sul piano yOz e sul piano xOz. Alla fine otterremmo due equazioni nelle tre variabili x, y e z, il cui sistema individua in modo univoco la retta nello spazio.

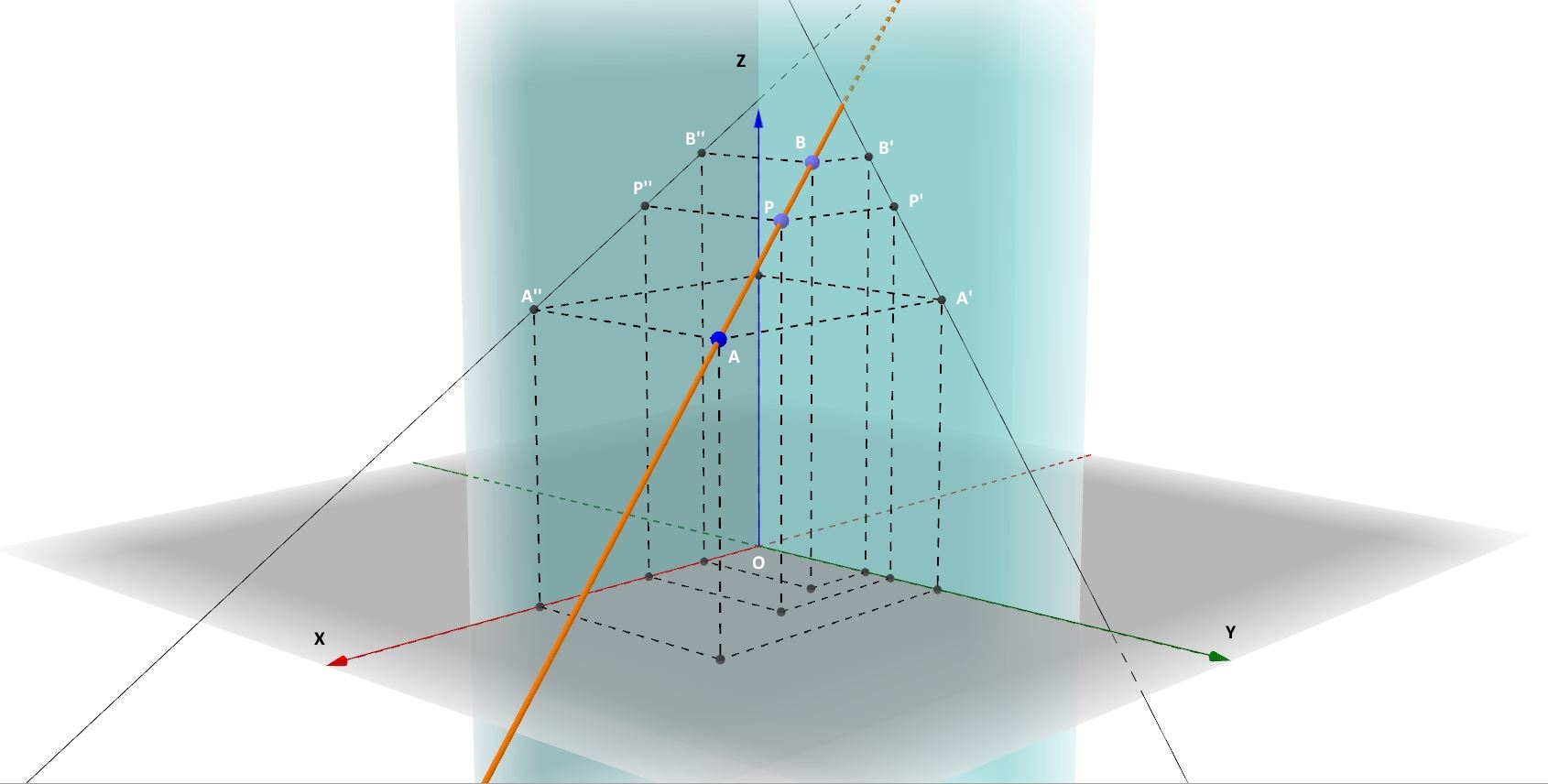
In altre parole, nello spazio la retta va vista come intersezione di due piani. Nella figura 5 è visibile la stessa retta delle figura 4, con evidenziati i piani dalla cui intersezione essa è generata:

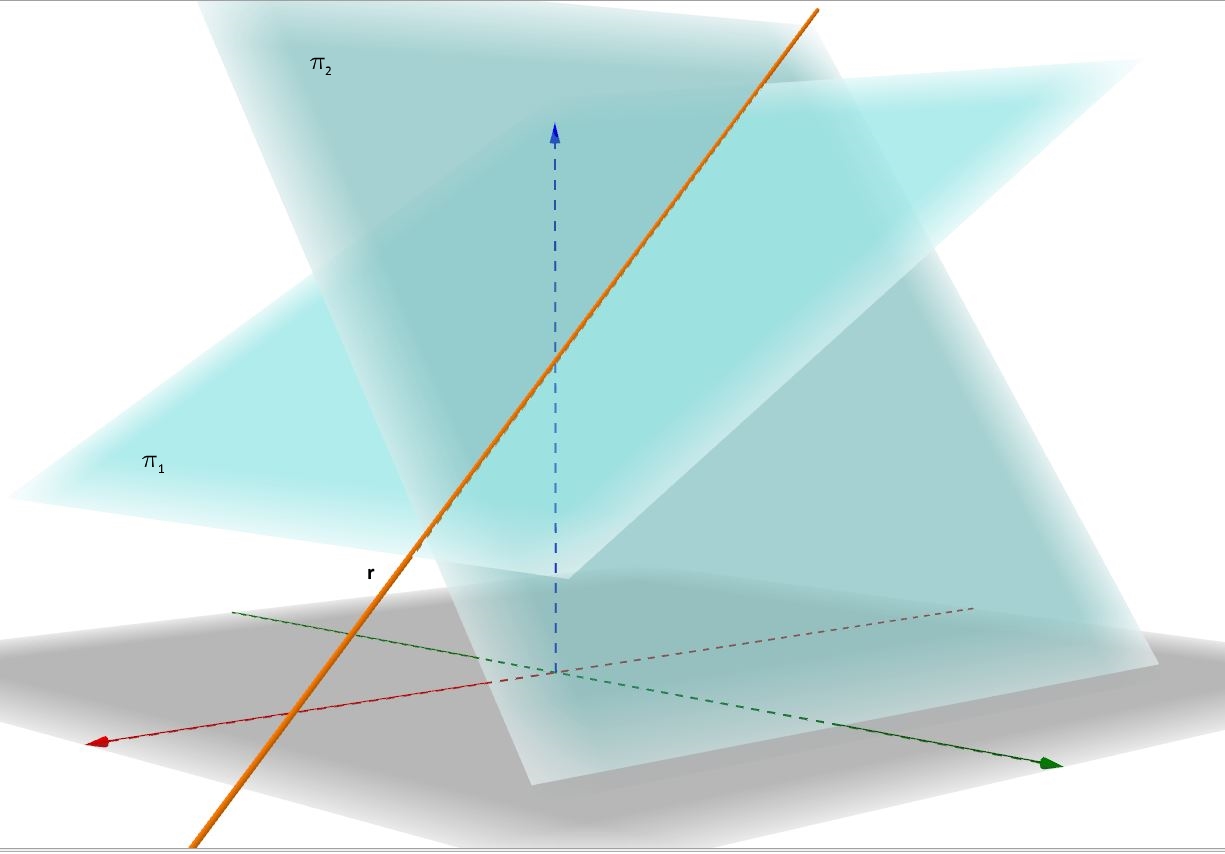
Per determinare l'equazione di una retta nello spazio, dobbiamo, pertanto, introdurre prima quella del piano.

Il piano e la retta come intersezione di piani

Restando nelle due dimensioni, cioè restando confinati sul piano cartesiano xOy, naturalmente non ci poniamo il problema di studiare il piano, proprio perché ci stiamo dentro, per cui ci è impossibile vederlo. Quando, invece, ci spostiamo nello spazio a tre dimensioni, possiamo visualizzarlo e determinarne l’equazione cartesiana. Anche in questo caso, torna utile il concetto di luogo geometrico. Di quale proprietà godono , allora, tutti i punti di uno stesso piano ?

Facciamo riferimento alla figura 6.

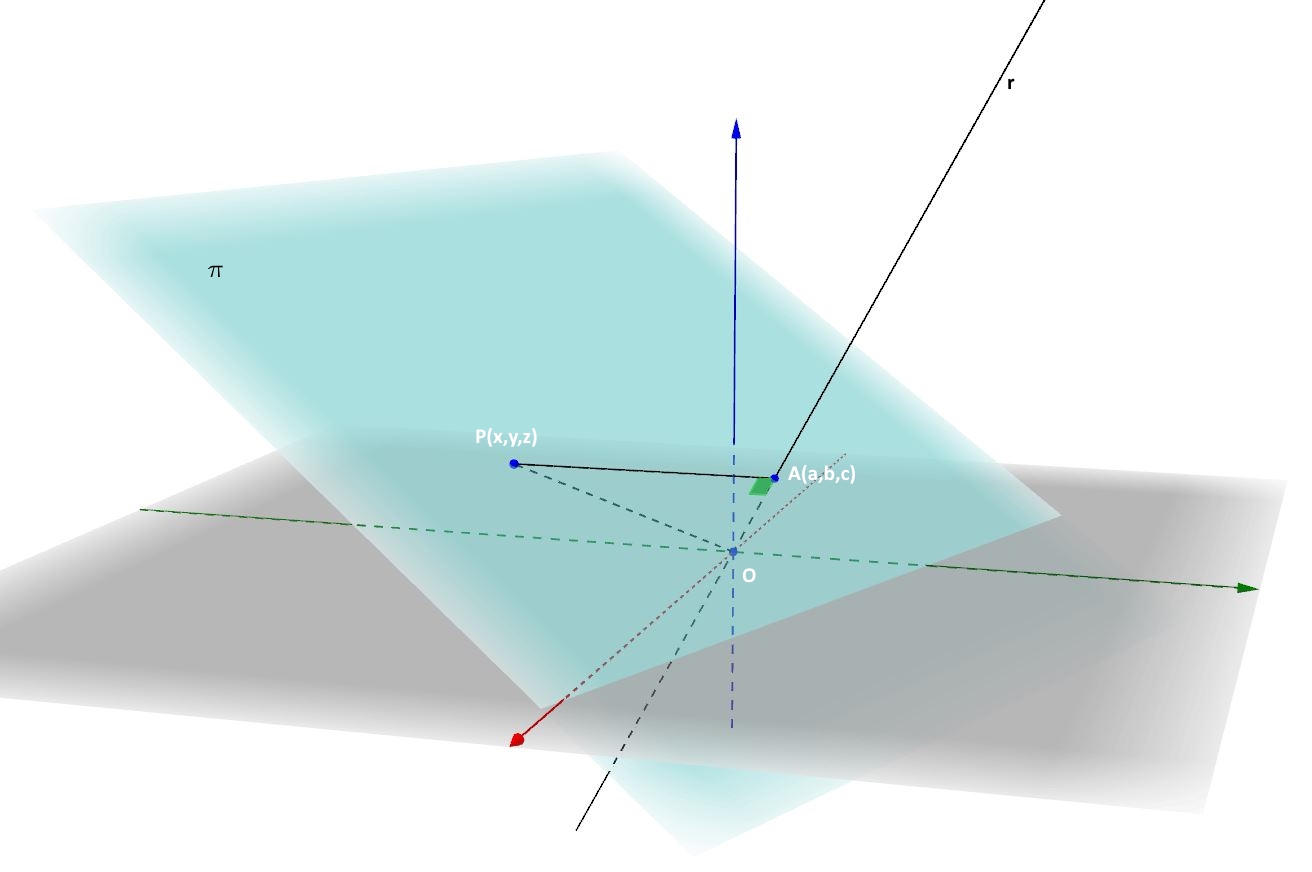
Consideriamo un generico piano π non passante per l’origine degli assi. Per l’origine degli assi facciamo passare invece la retta perpendicolare al piano π. Essa intersecherà il piano π nel punto A di coordinate spaziali che definiamo a, b, c. Prendiamo ora un qualsiasi punto P del piano π, le cui coordinate chiamiamo x, y, z.

Consideriamo il triangolo OAP. Esso è rettangolo in A perché la retta r è perpendicolare al piano, per costruzione, quindi qualsiasi retta appartenente al piano, tra cui quella passante per A e per P, sarà perpendicolare  alla retta r. Per il teorema di Pitagora, quindi, sarà:

                (5)

E’ proprio questa la proprietà di cui godono tutti i punti di uno stesso piano e che caratterizza, quindi, il piano come luogo geometrico.

A questo punto è necessario tornare per un attimo in due dimensioni e  ricordare che la distanza tra due punti A e B in geometria analitica del piano è data da:

              (6)

Questa formula si dimostra molto agevolmente considerando la figura 7

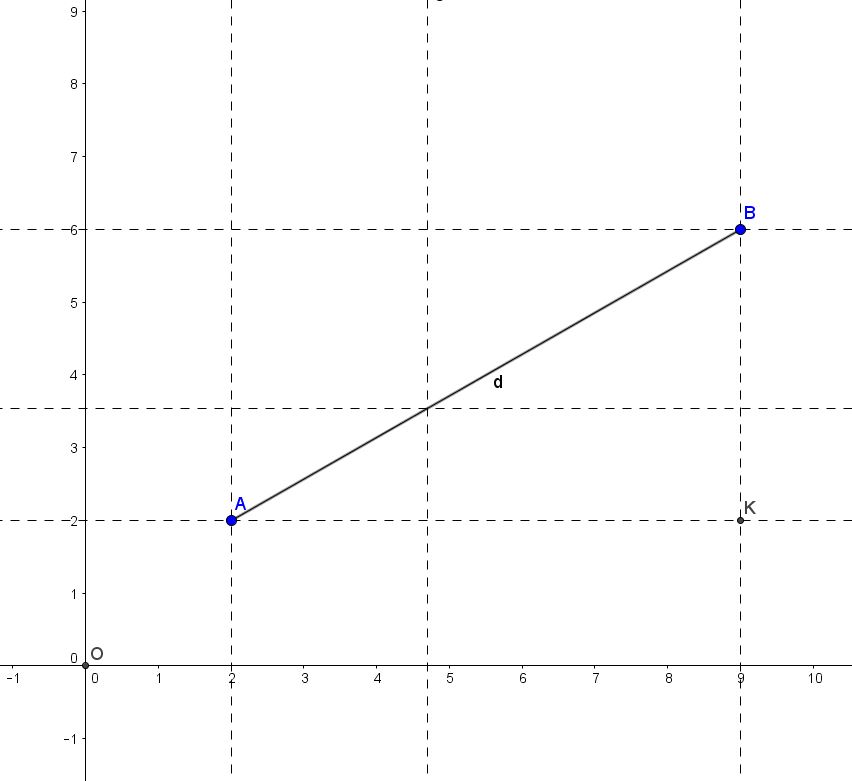
Applicando il teorema di Pitagora al triangolo rettangolo AKB, otteniamo:

Da cui, sostituendo ad    e     le espressioni      e    otteniamo subito la (6).

Nello spazio basta aggiungere sotto radice quadrata il termine relativo alla coordinata z, quindi:

Per rendersene conto basta considerare la figura 8:

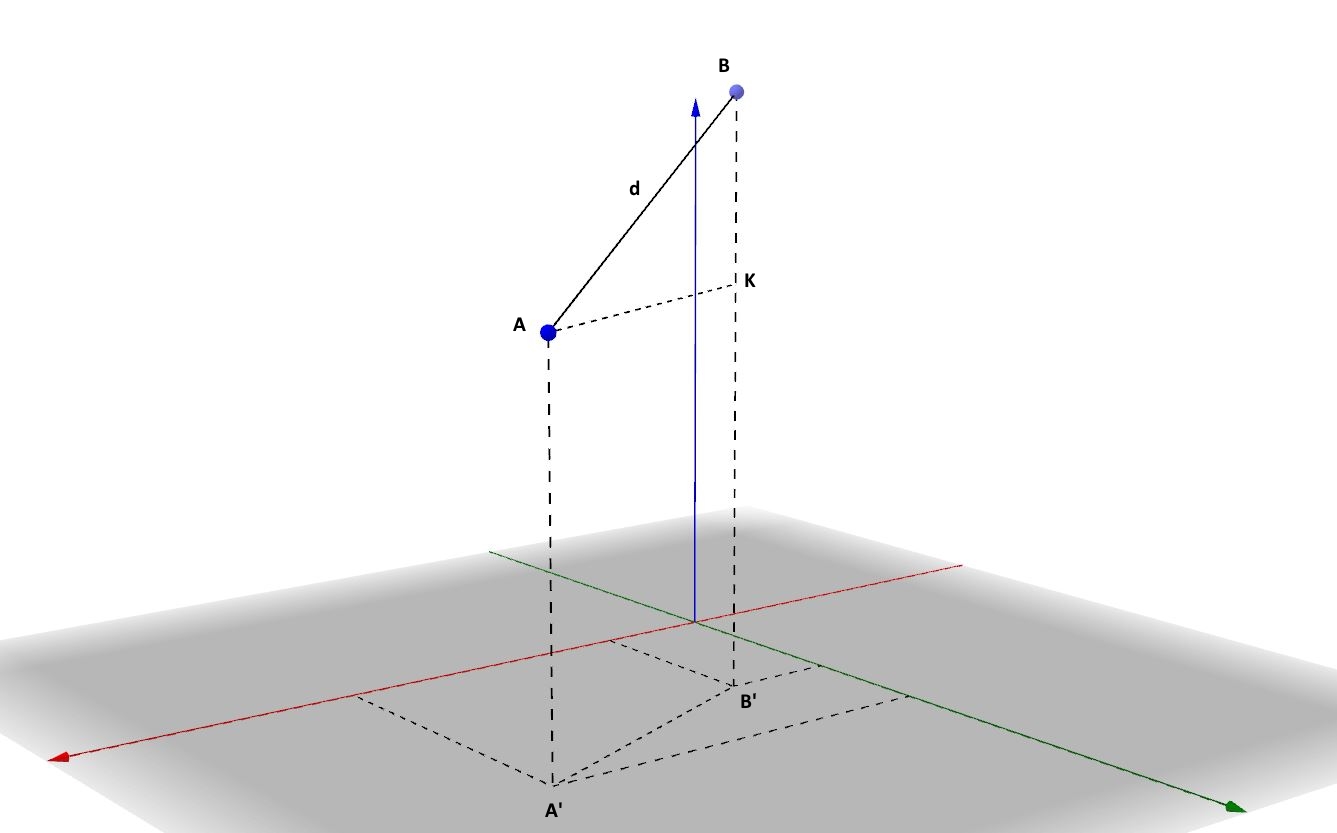
Applicando il teorema di Pitagora al triangolo rettangolo AKB, otteniamo anche in questo caso:

ma   ora è uguale alla distanza       (proiezione ortogonale di AB sul piano xOy) che a sua volta è data da:

mentre  è pari a . Quindi, in definitiva:

Applicando ora la suddetta formula alla (5) otteniamo:

Svolgendo i calcoli, portando tutto al primo membro e ordinando otteniamo:

                      (7)

Ponendo ora:

la (7) diventa:

ax+by+cz+d=0                        (8)

Questa è l’equazione del piano. Notiamo la somiglianza con quella della retta nel piano in forma implicita, con l’aggiunta del termine relativo alla coordinata z.

Considerando la retta nello spazio come generata dall’intersezione di due piani, per individuarla univocamente occorre , perciò, un sistema di due equazioni come la (8).

Facciamo un esempio.

Per semplicità, cerchiamo di individuare la retta r dello spazio parallela al piano xOz e al piano xOy, distante dal piano xOy una quantità pari a 5 e dal piano xOz una quantità pari a 3.

Facciamo riferimento alla figura 9.

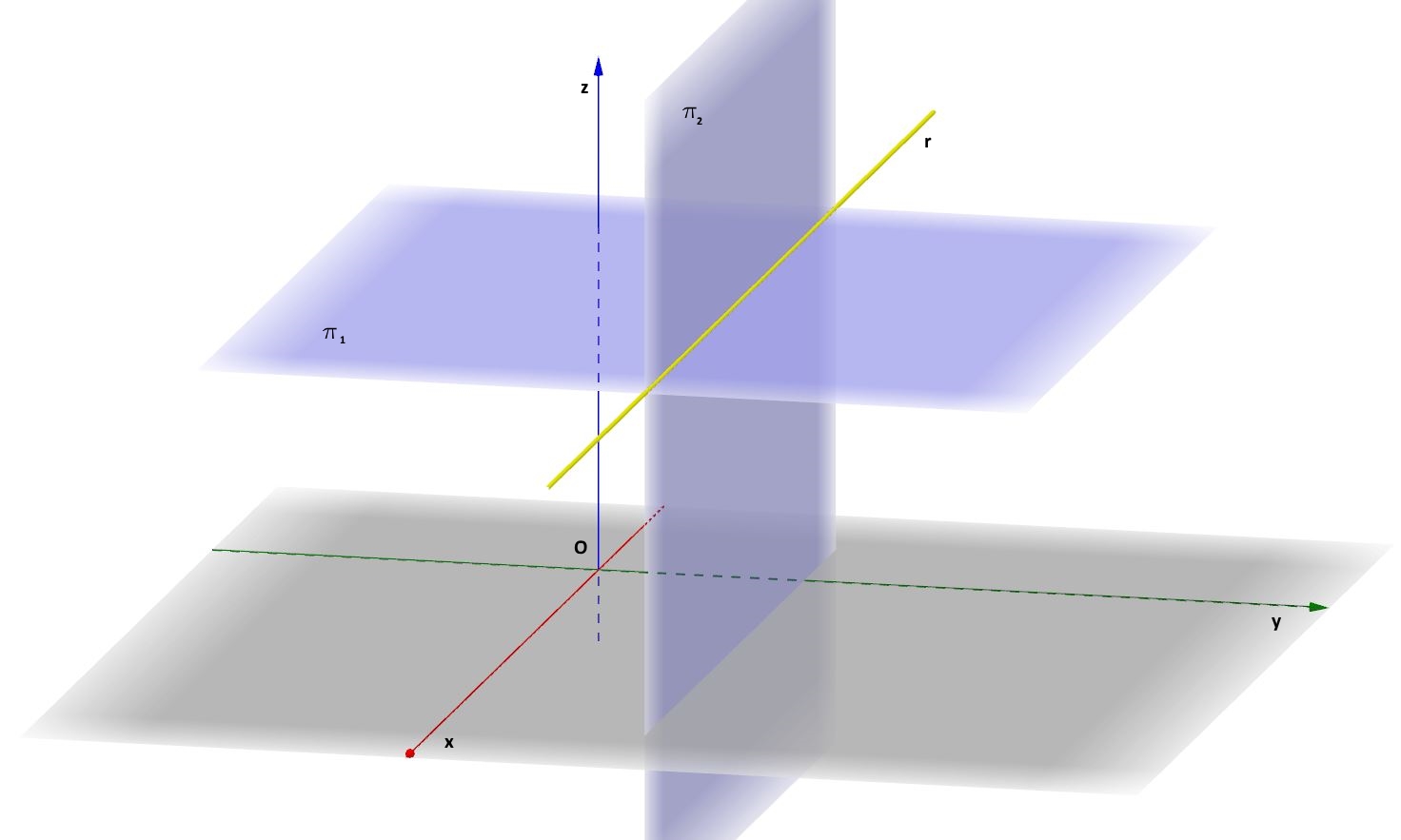
Tutti i punti di questa retta , dunque, avranno coordinata z=5 e coordinata y=3. Queste appena scritte possiamo interpretarle come le equazioni di due piani particolari. Rammentando la (8), infatti, si ottiene z=5 se poniamo a=0, b=0, c=1 e d=-5, mentre si ottiene y=3 se poniamo a=0, b=1, c=0 e d=-3.  “z=5” e “y=3”, quindi sono formalmente due casi particolari della (8). Di quali piani si tratta ? Cosa ci dice l’equazione z=5 ? Ci dice che qualsiasi punto di tale piano ha sempre la stessa coordinata z pari a 5. Ma questo quando accade ? Quando ci si muove su un piano parallelo a quello xOy.

L’equazione z=5, quindi, è l’equazione di un piano, che definiamo     , parallelo al piano xOy e distante 5 da quest’ultimo.

Analogamente, cosa ci dice l’equazione y=3 ? Ci dice che qualsiasi punto di tale piano ha sempre la stessa coordinata y pari a 3. Ma questo quando accade ? Quando ci si muove su un piano parallelo a quello xOz.

L’equazione y=3, quindi, è l’equazione di un piano, che definiamo  , parallelo al piano xOz e distante 3 da quest’ultimo.

In definitiva, la nostra retta r dello spazio è univocamente determinata dal sistema di equazioni:

z=5    (piano  )

y=3    (piano )

 

Nella seconda parte si parlerà di fasci di rette , fasci di piani e della sfera.