Troppa fatica per un quiz banalissimo, in cui i numeri hanno un valore decisivo! Come già detto nei commenti, provare per trovare...
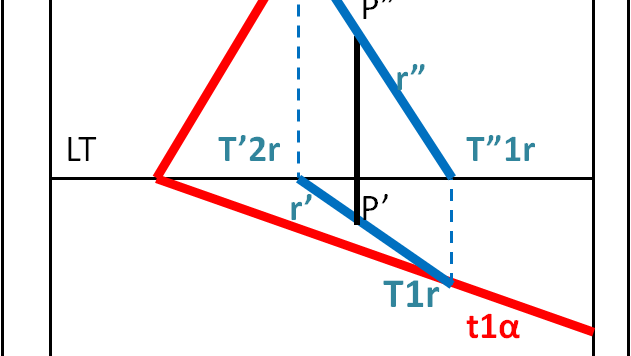
La geometria descrittiva di Monge continua, descrivendo il piano e le regole di appartenenza di un ente ad un altro.
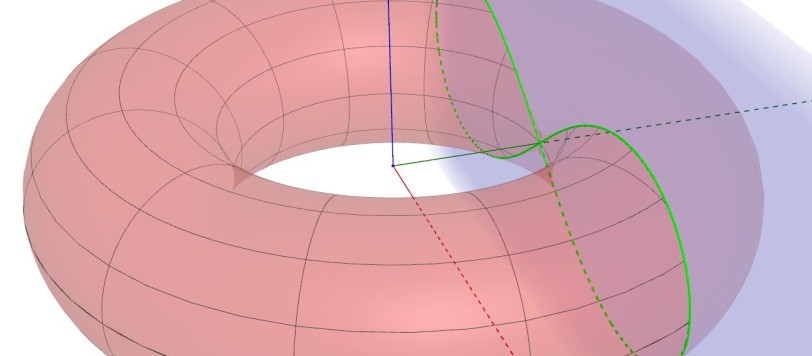
Rieccoci qui con l'ultima parte dell'appendice all'articolo 8° sulla geometria solida, dedicato al toro. Nella prima appendice abbiamo fatto la conoscenza delle circonferenze di Villarceau. In questa seconda appendice illustrerò altre interessanti curve ottenibili andando a sezionare il toro con un particolare piano. Ci serviremo, come sempre in geometria analitica dello spazio, del linguaggio della matematica. Ma niente paura, useremo strumenti semplici. E, in ogni caso, se avete dubbi, non avete che da chiedere nei commenti.
L'ultima volta avevo concluso l'articolo accennando alle sezioni spiriche, che sono proprio quelle di cui ci occupiamo questa volta. Intanto, perché si chiamano spiriche ?
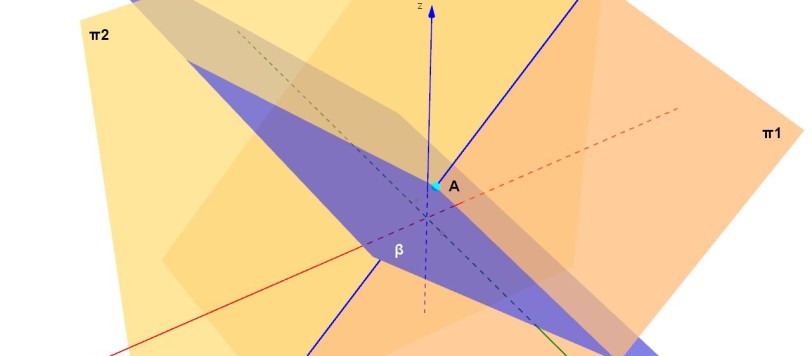
Nel precedente articolo, che potete rileggere QUI, ho introdotto il concetto di parametri direttori di una retta nel piano. In questo estendiamo il concetto alla retta nello spazio e al piano. Passiamo, quindi, nel riferimento cartesiano dello spazio.
Proseguiamo il nostro percorso nella geometria dello spazio con la seconda parte dell'articolo. La numerazione delle figure e delle formule segue quella della prima parte dell'articolo, che trovate QUI. Fasci di rette nel piano e fasci di piani nello spazio Nel piano le rette posso essere tra loro incidenti, quando hanno un punto in […]
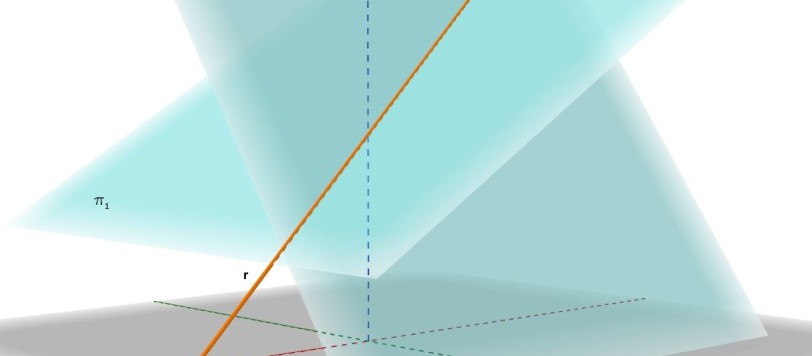
Obiettivo di questo articolo, di cui viene pubblicata ora la prima parte, è quello di entrare nell'affascinante mondo della geometria dello spazio e, dopo la seconda parte, dimostrare che la curva congiungente due punti situati su una superficie sferica e che misuri la minore distanza tra essi è un arco di circonferenza massima, ossia avente centro coincidente con quello della sfera.
Chi non ha mai visto una delle figure più usate in letteratura per rappresentare i buchi neri come deformazioni dello spazio-tempo? Mi riferisco ai celebri “imbuti”. Una geniale descrizione grafica che deve essere, però, capita con tutti i suoi enormi limiti. Cerchiamo di costruirla e di capire quanto sia “fittizia” e quanta confusione potrebbe creare se non interpretata correttamente.
Ho cercato il modo migliore per introdurre due numeri (o -meglio- concetti) fondamentali per la matematica, la geometria e la fisica. Ho trovato varie possibilità, anzi potrei dire che ne ho trovato infinite. E, allora, mi sono fermato se no rischiavo di mordermi la coda (che non ho… ve lo giuro!). Ho quindi deciso di agire a modo mio. L’importante è che alla fine si riesca a comprendere con chi abbiamo a che fare.