25/06/16

introduzione alla geometria dello spazio - seconda parte **

Categorie: Articoli Matematica Tags: fascio di piani fascio di rette geometria piano retta sfera Scritto da: Arturo Lorenzo Commenti:16

Proseguiamo il nostro percorso nella geometria dello spazio con la seconda parte dell'articolo. La numerazione delle figure e delle formule segue quella della prima parte dell'articolo, che trovate QUI.

Fasci di rette nel piano e fasci di piani nello spazio

Nel piano le rette posso essere tra loro incidenti, quando hanno un punto in comune, o parallele, quando non hanno alcun punto in comune oppure quando coincidono. Le infinite rette incidenti in un punto formano quello che si definisce un fascio proprio di rette.

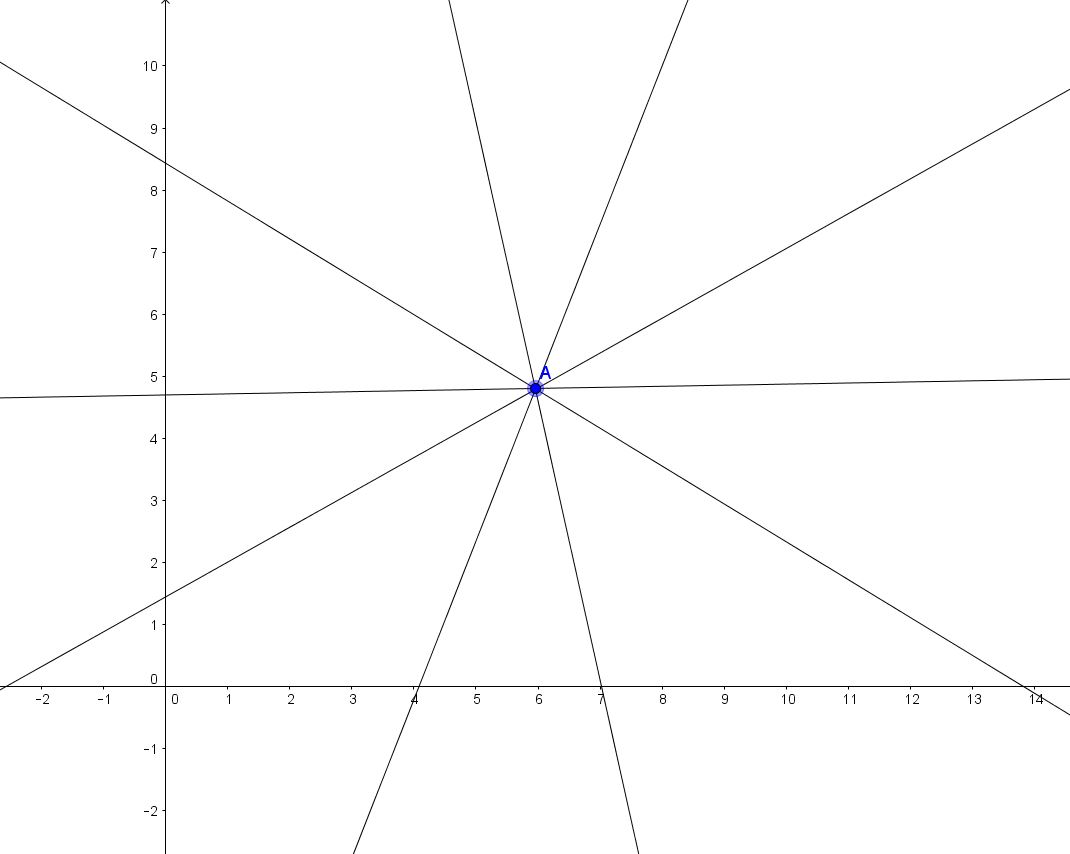
Le infinite rette tra loro parallele formano, invece, quello che si definisce fascio improprio di rette.

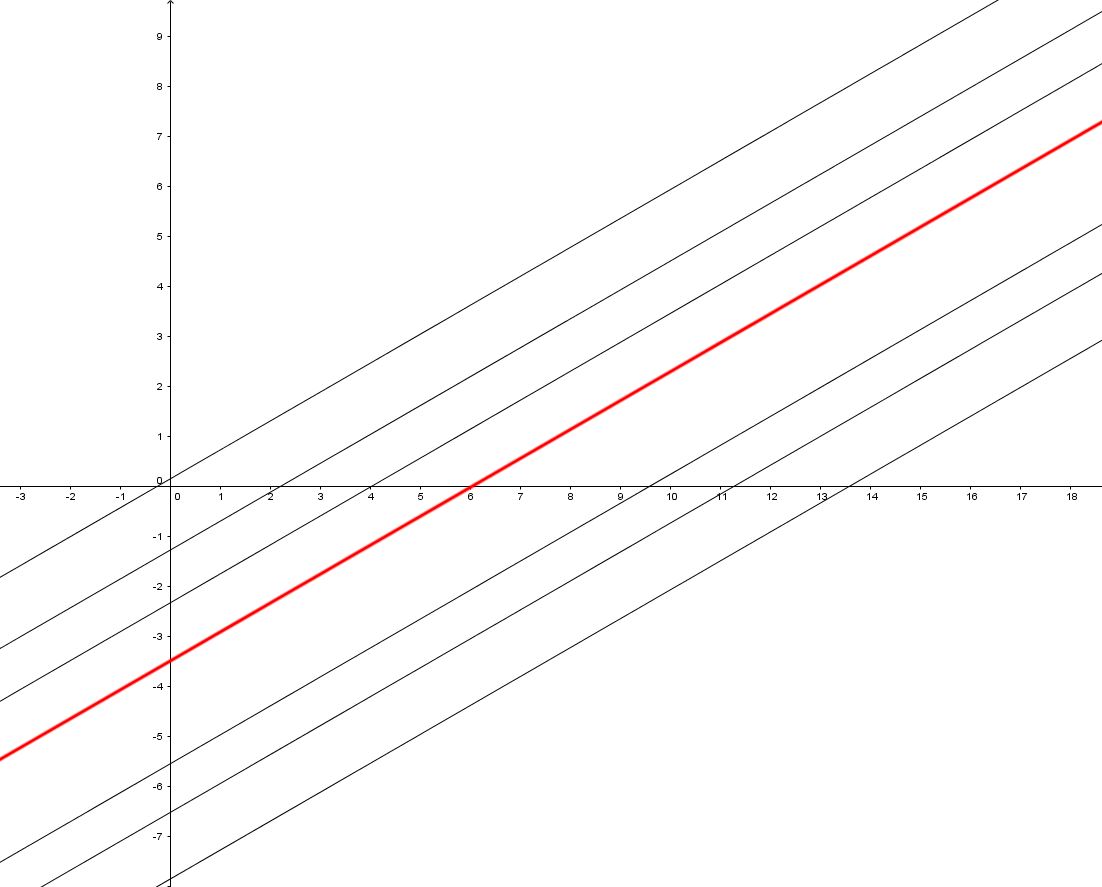
Come trovare l’espressione analitica di ciascun tipo di fascio ?

Consideriamo il fascio proprio. Tutte le rette del fascio proprio passano per lo stesso punto P, detto centro o sostegno del fascio. Le coordinate del punto P, quindi, devono soddisfare l’equazione della generica retta del fascio. Riprendiamo l’equazione della retta in forma esplicita nel piano:

y= mx + q (9)

e sostituiamo a x e y le coordinate, note, del punto P

$y_{p}=mx_{p}+q$

da cui

$q=y_{p}-mx_{p}$

sostituiamo questa espressione di q nella (9), ordiniamo e otteniamo:

$y-y_{p}=m(x-x_{p})$ con m variabile (10)

al variare del parametro m, otterremo tutte le infinite rette del fascio proprio con centro nel punto P, tranne la retta di equazione $x=x_{p}$ , che pure appartiene al fascio (anche essa, infatti, passa per il punto P). Ma possiamo ottenere anche questa dividendo tutto per m e riscrivendo, quindi, la suddetta equazione come:

$\frac{y-y_{p}}{m}=x-x_{p}$

Così si vede che per m tendente a infinito, si ottiene proprio $x=x_{p}$ .

L'equazione (10), in definitiva, è quella del fascio proprio di rette con centro nel punto P di coordinate $x_{p}$ e $y_{p}$ .

Consideriamo ora il fascio improprio di rette. In questo caso il coefficiente angolare m è lo stesso per tutte le rette del fascio e ciò che varia è invece il termine q. L’equazione del fascio improprio, quindi, si ottiene semplicemente da quella in forma esplicita di una retta, considerando m costante e q variabile:

$y=m_{o}x+k$ (con k variabile)

L’equazione del fascio proprio e di quello improprio di rette possono essere ottenute anche partendo da due rette qualsiasi appartenenti al fascio, a nostra scelta. Questo è un ragionamento che ci torna utile nello studio del fascio proprio di piani.

Consideriamo, allora, due rette di equazione implicita

retta r : $a{_{1}}x+b{_{1}}y+c{_{1}}=0$

retta s : $a{_{2}}x+b{_{2}}y+c{_{2}}=0$

Se sommo il primo membro della prima equazione con il primo membro della seconda, moltiplicandolo per un parametro variabile k, ottengo:

$a_{1}x+b_{1}y+c_{1}+k(a_{2}x+b_{2}y+c_{2})=0$ (11)

che è in pratica una combinazione lineare delle due equazioni. Vediamo cosa succede alla (11) al variare del parametro k. Per k=0, otteniamo l’equazione della retta r. Se poi scriviamo la (11) dividendo tutto per k, si ha:

$\frac{1}{k}(a_{1}x+b_{1}y+c_{1})+a_{2}x+b_{2}y+c_{2}=0$

Dalla suddetta si vede che per k tendente a infinito otteniamo l’equazione della retta s. Per tutti gli altri valori di k otteniamo tutte le altre rette del fascio.

In definitiva, l’equazione di un fascio di rette può scriversi partendo da quelle di due qualsiasi rette del fascio, mediante una loro combinazione lineare.

Spostiamoci ora nuovamente nello spazio tridimensionale. Qui interessano i fasci di piani. Anche i piani formano fasci propri e fasci impropri. Il fascio proprio di piani è quello composto dagli infiniti piani aventi come sostegno una data retta. Si può immaginare di ruotare un piano attorno ad una retta, generando in tal modo tutti i piani del fascio avente come sostegno quella retta.

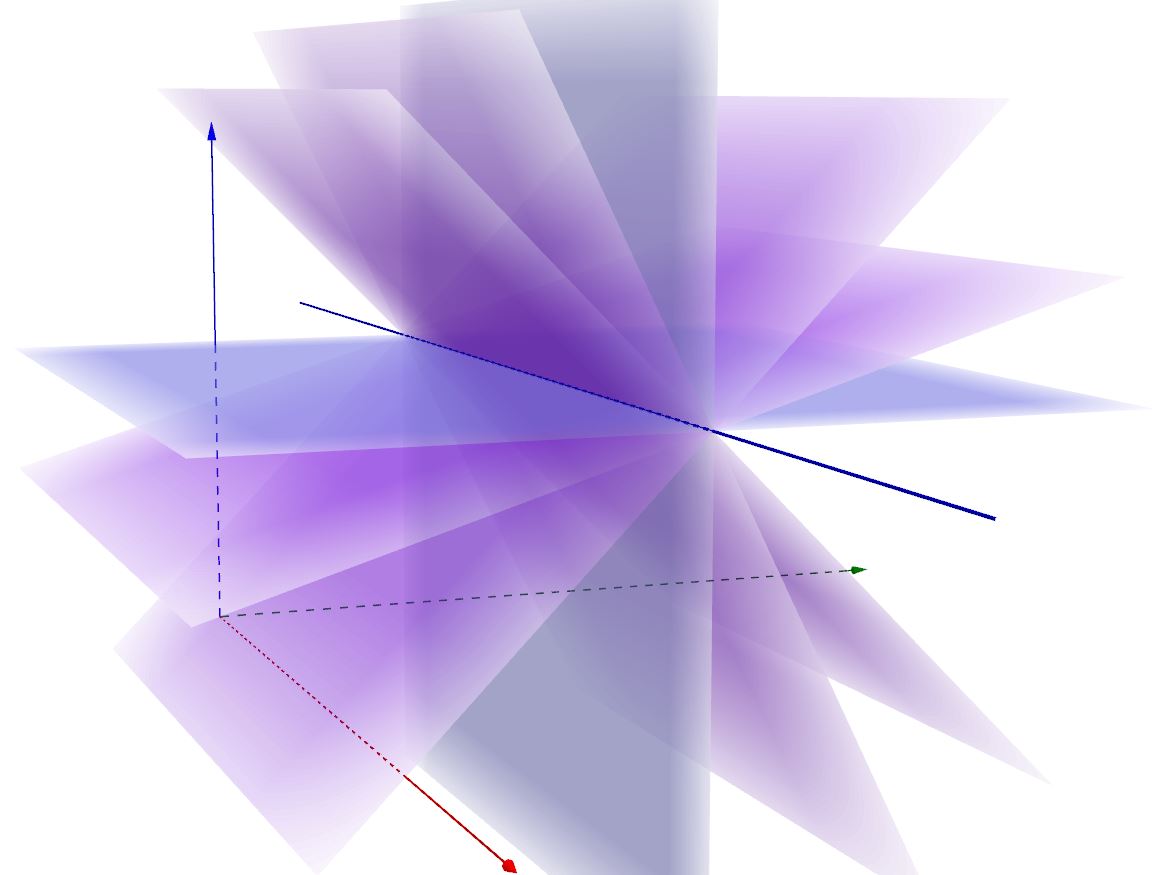
Il fascio improprio di piani, invece, è composto dagli infiniti piani paralleli ad un dato piano.

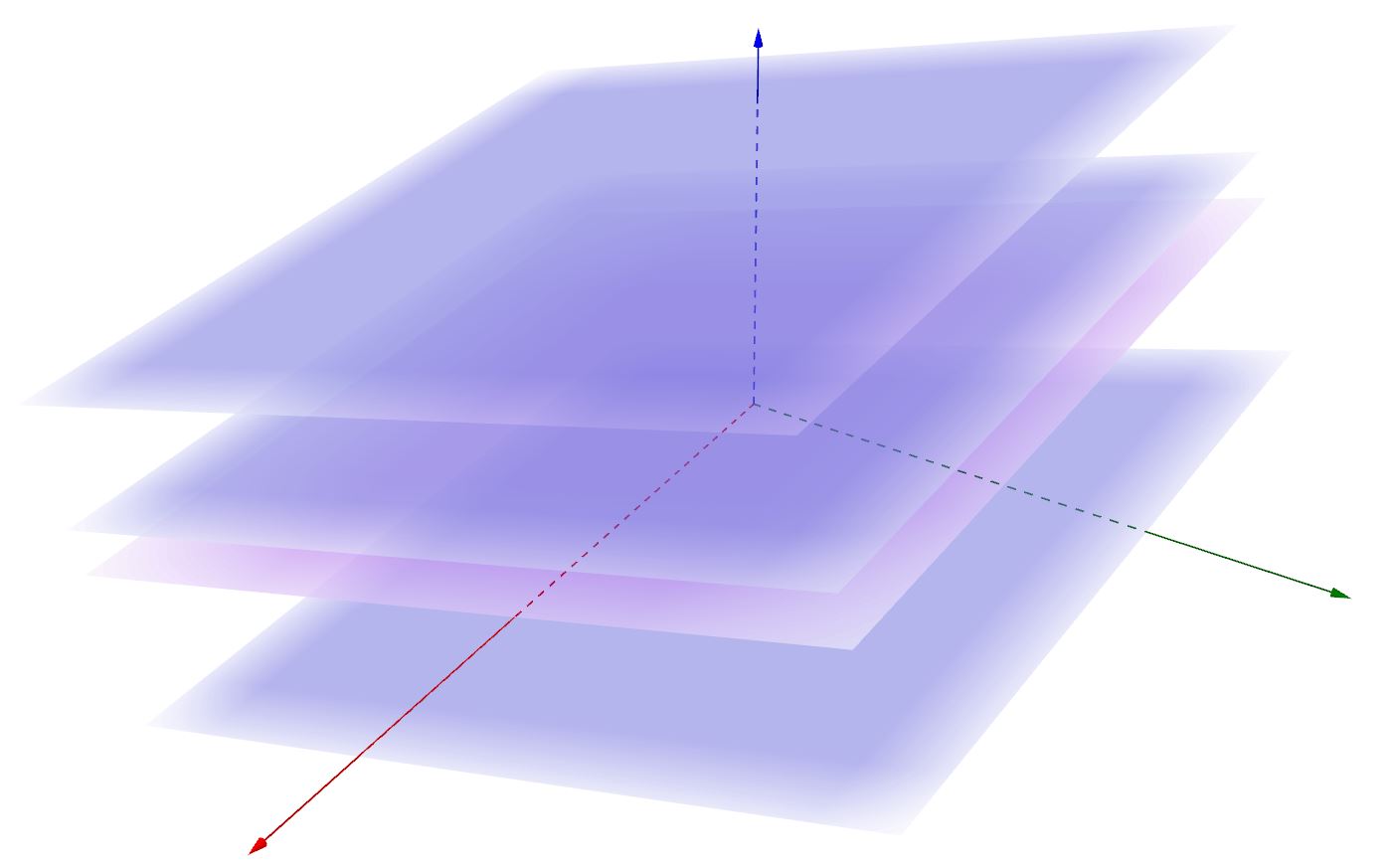
Analogamente a quanto detto per i fasci di rette nel piano, si arriva all’equazione di un fascio di piani mediante una combinazione lineare delle equazioni di due qualsiasi piani del fascio, scelti a piacimento. Siano date, quindi, le equazioni di due piani del fascio:

piano $\pi_{1}=a_{1}x+b_{1}y+c_{1}z+d_{1}=0$

piano $\pi_{2}=a_{2}x+b_{2}y+c_{2}z+d_{2}=0$

Se sommo il primo membro della prima equazione con il primo membro della seconda, moltiplicandolo per un parametro variabile k, ottengo:

$a_{1}x+b_{1}y+c_{1}z+d_{1}+k(a_{2}x+b_{2}y+c_{2}z+d_{2})=0$ (12)

In analogia a quanto visto per i fasci di rette nel piano, anche in questo caso per k=0 otteniamo l’equazione del piano $\pi_{1}$ , mentre dividendo tutti i termini della (12) per k si ha che per k tendente ad infinito otteniamo l’equazione del piano $\pi_{2}$ . Per tutti gli altri valori di k otteniamo tutti gli altri piani del fascio.

Facciamo un esempio.

Vogliamo determinare l’equazione del fascio proprio di piani aventi come sostegno la retta dello spazio individuata dal sistema di equazioni:

z=5

y=3

Per quanto abbiamo visto nell’esempio fatto a proposito della retta come intersezione di due piani, questa retta è generata dall’intersezione dei piani di equazione z=5 e y=3 rispettivamente. Equazioni che possiamo scrivere come z-5=0 e y-3=0. Possiamo, quindi, determinare l’equazione del fascio cercato facendone la combinazione lineare:

z-5+k(y-3)=0 (13)

svolgendo i calcoli:

ky+z-(5+3k)=0

Questa è l’equazione del fascio. Al variare del parametro k otterremo tutti gli infiniti piani del fascio. In particolare, per k=0 otteniamo z=5 e, se dividiamo tutto per k e scriviamo la (13) come

$\frac{z-5}{k}+y-3=0$

per k tendente ad infinito otteniamo y=3.

La sfera e la superficie sferica

La sfera è un solido particolare che incontriamo molto spesso non solo in geometria dello spazio ma anche in Natura. La superficie sferica, invece, è l"involucro" della sfera. La sfera gode di una perfetta simmetria spaziale, per cui, per esempio, con qualunque piano la sezioniamo, otteniamo sempre, come intersezione tra piano e superficie della sfera, una circonferenza. Non avviene la stessa cosa, invece, con coni e cilindri retti, che pure hanno una simmetria ma solo assiale.

Anche la sfera e la superficie sferica sono luoghi geometrici. In particolare, tutti i punti della la superficie sferica godono della proprietà per cui è costante, e pari al raggio, la distanza dal centro. Vediamo di tradurre in forma analitica questa proprietà, dunque di trovare l'equazione della superficie sferica.

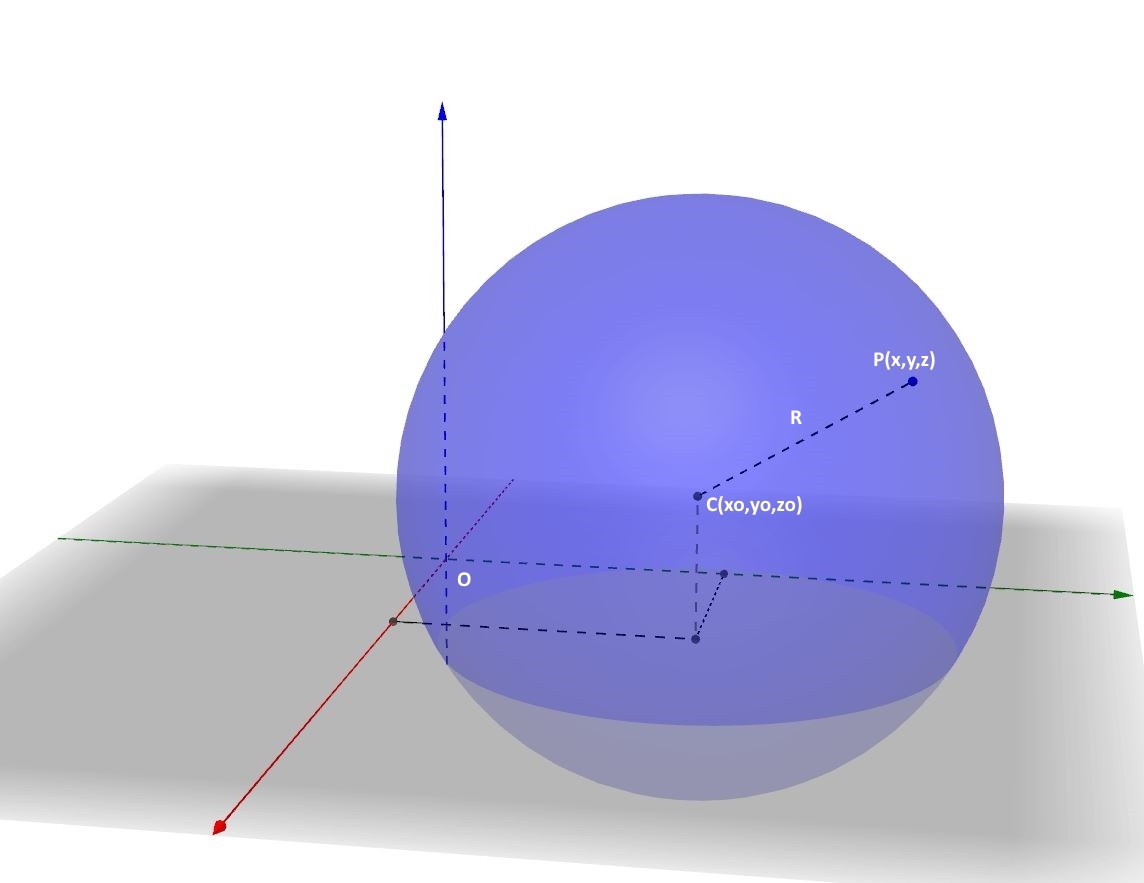
Se chiamiamo con x, y, z le coordinate di un generico punto della superficie della sfera e con xo, yo, zo le coordinate del suo centro, rammentando la formula della distanza tra due punti in geometria analitica dello spazio, ricaviamo subito l’equazione che caratterizza questo luogo geometrico:

$\overline{CP}^2=R^2=(x-x_{o})^2+(y-y_{o})^2+(z-z_{o})^2$

Svolgendo i calcoli, portando tutto a primo membro e ordinando, otteniamo:

$x^2+y^2+z^2-2x_{o}x-2y_{o}y-2z_{o}z-R^2+x_{0}^{2}+y_{0}^{2}+z_{0}^{2}=0$ (14)

Ponendo ora:

$a=-2x_{o}$

$b=-2y_{o}$

$c=-2z_{o}$

$d=-R^2+x_{o}^{2}+y_{o}^{2}+z_{o}^{2}$

possiamo scrivere la (14) come:

$\mathbf{x^2+y^2+z^2+ax+by+cz+d=0}$ (15)

Questa è, dunque, l’equazione della superficie della sfera. Per come abbiamo definito i coefficienti a, b, c, d, è immediato che, partendo dalla equazione (15), le coordinate del centro saranno date da:

$x_{o}=-\frac{a}{2}$

$y_{o}=-\frac{b}{2}$

$z_{o}=-\frac{c}{2}$

mentre il raggio sarà dato da:

$R=\sqrt{x_{o}^{2}+y_{o}^{2}+z_{o}^{2}-d}=\sqrt{(-\frac{a}{2})^2+(-\frac{b}{2})^2+(-\frac{c}{2})^2-d}$

Una superficie sferica particolare è quella con centro nell’origine degli assi. In questo caso è:

$x_{o}=0$

$y_{o}=0$

$z_{o}=0$

quindi:

$a=0$

$b=0$

$c=0$

$d=-R^2$

Per cui la (15) diventa più semplicemente:

$\mathbf{x^2+y^2+z^2=R^2}$

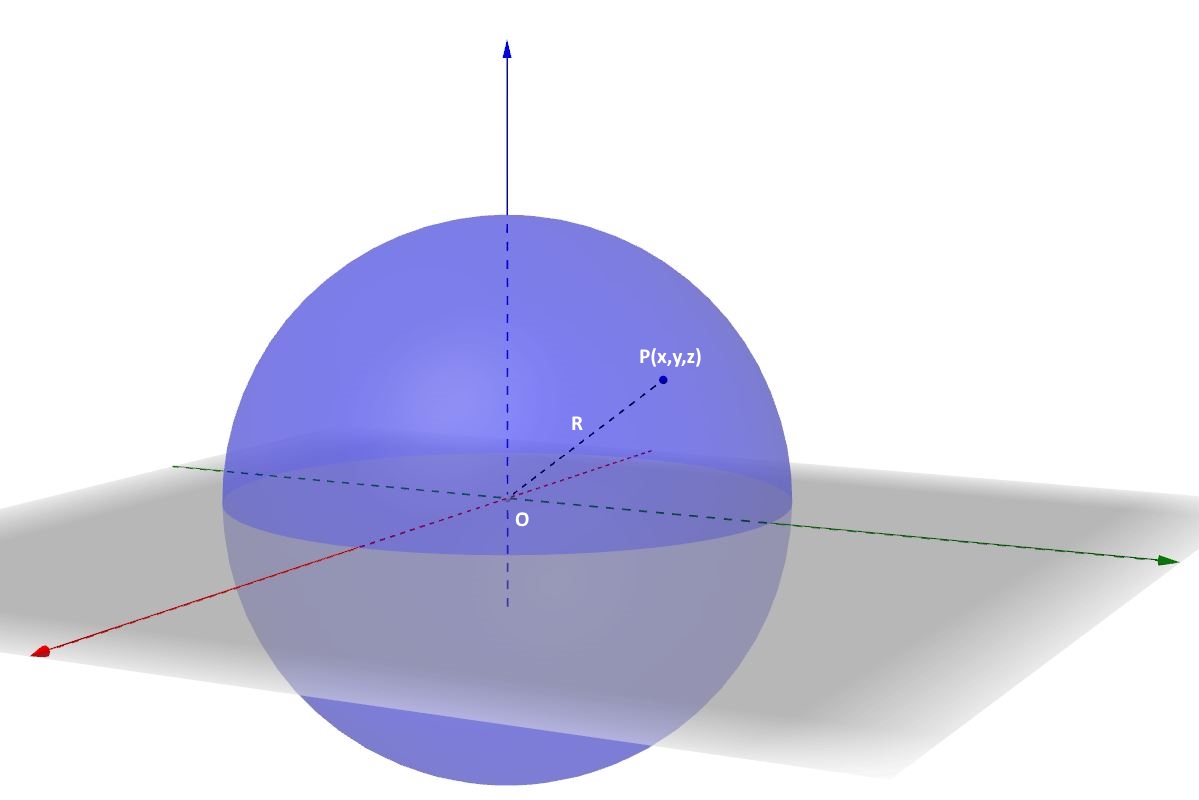
E' appena il caso di constatare che l'equazione della superficie sferica (15) è molto simile a quella della circonferenza nel piano

$\mathbf{x^2+y^2+ax+by+c=0}$ (equazione della circonferenza nel piano)

differenziandosi da quest'ultima solo per i termini relativi alla terza dimensione z. Tutte le formule relative alla superficie sferica (coordinate del centro e raggio) sono molto simili alle formule omologhe della circonferenza, con l'aggiunta dei termini relativi alla terza dimensione z.

Se, infine, dovessimo definire la sfera in termini di luogo geometrico, così come abbiamo fatto per la superficie sferica, dovremmo dire che essa è il luogo dei punti dello spazio la cui distanza dal centro è minore o al più uguale al raggio. Per la sfera con centro nell'origine, cioè, ciò che traduce in forma analitica la proprietà dei suoi punti è la disequazione:

$\mathbf{x^2+y^2+z^2\leq R^2}$

Nel prossimo articolo dimostreremo che, dati due punti su una superficie sferica, la curva che li congiunge e che misura la minore distanza tra i due punti è un arco di circonferenza massima, avente centro coincidente con quello della superficie sferica.

16 commenti

Arturo Lorenzo

28/06/2016 at 14:49

Aggiungo un quiz facile facile, per assicurarmi di avere scritto in modo comprensibile l'argomento fasci di piani e rette nello spazio e anche per creare un po' di discussione sull'argomento.

Quale è l'equazione del fascio proprio di piani avente come sostegno l'asse z ?
Pippo

28/06/2016 at 22:23

$x + ky = 0$ ……..(1)

$k \epsilon R$

ovvero, in maniera migliore ( forma implicita ) :

$ax + by = 0$ ……(2)

scritta in modo da evitare , nella (1) , di dividere per k e farlo tendere a infinito per ottenere il piano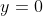 $y = 0$ . Non si otterrebbe comunque tale piano così , perché " tendere all'infinito" non è " diventare infinito" . Nessun numero, nessuna variabile, "diventa" infinita . La retta numerica è illimitata .

Comunque, sia la (1) che la (2) rappresentano , nel piano xy , l'equazione di una retta che passa per l'origine (con la precisazione detta per la (1) , che esclude l'asse x , di equazione y = 0 )

LA (1) o la (2) , nello spazio rappresentano piani del fascio avente per sostegno l'asse z .
Pippo

28/06/2016 at 23:01

Chiedo scusa , mi è partito l'invio prima di completare.

Quei piani del fascio anzidetti, intersecano il piano xy nelle rette che , in tale piano, hanno la stessa equazione .
Arturo Lorenzo

28/06/2016 at 23:05

Grazie Pippo per avere dato il tuo contributo alla discussione. Aspettiamo altre risposte.
Umberto

29/06/2016 at 17:08

Forse non è stato ancora detto esplicitamente che l'asse z è l'intersezione dei piani xz (di equazione y=0) e yz (di equazione x=0) Il sistema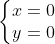 $\left\{\begin{matrix} x=0\\ y=0 \end{matrix}\right.$ ha come soluzioni l'asse z, pertanto l'equazione del fascio è la combinazione lineare dei due piani y=0, x=0, ovvero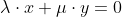 $\lambda \cdot x +\mu \cdot y=0$
Arturo Lorenzo

29/06/2016 at 23:55

Bene, ringrazio anche Umberto per il suo contributo alla discussione.

All'equazione del fascio di piani richiesto, secondo quanto illustrato in questa seconda parte dell'articolo, si giunge considerando due qualsiasi piani del fascio, individuando le rispettive equazioni e facendone una combinazione lineare. Naturalmente andremo a considerare due piani semplici, ossia il piano xOz e il piano yOz. Il piano xOz è il luogo geometrico dei punti dello spazio aventi la coordinata y=0. Quest'ultima è proprio l'equazione di tale piano. Tutti i suoi punti, infatti, potranno avere coordinate x e z qualsiasi, ma avranno la coordinata y=0. Analogamente, il piano yOz è il luogo geometrico dei punti dello spazio aventi la coordinata x=0 e questa è proprio l'equazione di tale piano. Tutti i suoi punti, infatti, potranno avere coordinate y e z qualsiasi, ma avranno la coordinata x=0. Note, dunque, le equazioni di due piani del fascio, ne facciamo una combinazione lineare, ossia sommiamo la prima alla seconda, moltiplicando la seconda per un parametro o moltiplicando ciascuna per un proprio parametro. Possiamo cioè avere:

x=0 e y=0 ---> x+ky=0 (con k reale)

oppure

x=0 e y=0 ---> ax+by=0 (con a e b reali)

dalla prima si passa immediatamente alla seconda ponendo k=b/a.

Con la prima, tuttavia, così come è scritta, resterebbe esclusa dal fascio l'equazione y=0 nel senso che per qualsiasi valore di k non potremmo mai ottenere y=0. A meno di non ricorrere all'artificio esposto nell'articolo, ossia quello di dividere tutto per k e far tendere quest'ultimo a infinito. In tal caso possiamo dire che, al limite, per k tendente ad infinito, includiamo nel fascio anche il piano di equazione y=0.

In definitiva, entrambe le risposte, quella di Pippo e quella di Umberto, sono corrette ed esaurienti.

Il concetto che ritengo importante evidenziare è quello dell'equazione di un fascio proprio di piani determinata partendo da due qualsiasi piani del fascio. Chiaro che, potendo essere due piani qualsiasi, andrò a scegliere quelli più "comodi"
Pippo

30/06/2016 at 04:29

Salve Arturo e Umberto.

Questo è un OT , chiedo scusa .

Vorrei sapere come si fa a produrre ed inserire disegni , del tipo di quelli che vedo in giro qui. Il penultimo tasto posto qui sopra nella barra degli strumenti non aiuta molto.

Grazie .
Umberto

30/06/2016 at 06:39

Pippo, il tasto è quello prima di fx in alto a destra; il fatto è che lì devi inserire un url web, ovvero un link ad una immagine che prima devi aver messo su qualche sito web; io uso questo sito: http://imgur.com/

io poi per produrre semplici disegni uso questo: https://svg-edit.github.io/svgedit/releases/svg-edit-2.8.1/svg-editor.html
Pippo

30/06/2016 at 11:04

Grazie Umberto, ci proverò .

Ma trovo che in questo blog c'è qualche handicap : non si riesce a "salvare una bozza " di un messaggio , che non è concluso ma si deve interrompere per qualche ragione . E non si può vedere una "anteprima" di ciò che si è scritto, prima dell'invio . Ho frequentato altri forum , dov'è queste funzioni sono previste, e sono utili. Va bene , ci accontentiamo !

Ma dimmi : se faccio un disegno con Geogebra, che conosco un po' , devo comunque salvarlo sul web come hai detto, per poi poterlo pubblicare ?
Vincenzo Zappalà

30/06/2016 at 11:48

caro Pippo,

questo blog mira più al contenuto che al contenitore. Oltretutto, è gestito da una bravissimo amico che lo fa non solo gratuitamente, ma anche nei pochi ritagli di tempo. Come vedi non abbiamo nessuna pubblicità e già questo ne fa una mosca bianca... Quindi, non posso che consigliarti di ... accontentarti e usare procedure magari antiquate, ma sicuramente efficaci. Pensa che io, per molti anni, ho collaborato con colleghi americani, pubblicando insieme, quando ancora non esisteva la email e si comunicava con le lettere (sai quei pezzi di carta che si mettono dentro le buste e si appiccica un francobollo almeno un mese tra andata e ritorno... per non parlare di Gauss che ha calcolato le sue orbite a mano...). A parte gli scherzi, si cerca di migliorare, ma con piccoli passi... Se hai proposte concrete e fattibili semplicemente contatta Marko e appena possibile ci proverà.

Ad esempio, se uno vuole scrivere un commento lungo, che può interrompere, basterebbe scriverlo in word e poi fare il copia e incolla... Siamo sempre troppo spinti verso la pappa pronta: un po' di difficoltà non può che aiutare la mente e la fantasia...
Umberto

30/06/2016 at 14:14

si Pippo devi comunque salvarlo e trasferirlo sul web in un formato immagine (gif, jpg, bmp..) non so bene come funzioni geogebra;

Non so poi cosa intendi sull'anteprima; il messaggio e anche le immagini le potrai vedere e anche le formule inserite con la funzione fx; di sicuro non puoi salvare per spedirlo in altra occasione, ma se lo lasci sul tuo browser puoi spedirlo quando vuoi. non penso (oppure non so) se altri blog permettano il salvataggio di un materiale misto come questo
Pippo

30/06/2016 at 15:26

Grazie Umberto.

Si, altri blog permettono il salvataggio di materiale misto . L' " anteprima " è una funzione che permette a chi scrive di dare un'ultima controllata a quello che ha scritto, leggendo proprio quello che poi verra pubblicato, prima dell'invio .
Pippo

08/07/2016 at 13:54

Umberto, questo è ancora un OT.

Scusami ma io per certe cose sono proprio una frana. Ho provato come mi hai detto per caricare una immagine qui. Ho fatto il disegno ( con Geogebra, che conosco un po') , l'ho "esportato" come immagine con estensione .png ; poi sono andato sul sito che mi hai indicato "Imgur" , lí ho caricato l'immagine , e il sito mi ha dato un indirizzo web. L'ho copiato, poi sono venuto qui, ho cliccato sulla icona della barra comandi che precede fx ; mi si è aperta una casella , con una finestrella dove ho incollato quell'indirizzo web , e ho dato l'invio.

A questo punto, mi aspettavo di vedere l'immagine nel messaggio che sto digitando. Invece, mi compare un rettangolino con un bel punto interrogativo in centro, il che vuol dire forse che non è tutto andato a buon fine.

Come faccio a controllare, prima di pubblicare?

Per esemplificare, ora provo con il disegno di un cerchio , ripetendo la procedura e mettendolo qui . Vediamo che succede .
Pippo

08/07/2016 at 13:56

Ecco, succede che rimane il punto interrogativo nel riquadro. Quindi ho sbagliato qualcosa .

Potresti aiutarmi a capire che cosa ? Grazie
Umberto

08/07/2016 at 15:54

è sbagliato il link; quello che hai scritto è http://i.imgur.com/Shbqxu6

manca .png; il link giusto è questo:http://i.imgur.com/Shbqxu6.png

se il link è giusto, vedi subito l'immagine in anteprima:
Pippo

08/07/2016 at 16:36

Ti ringrazio tanto ! Ma il link completo non dovrebbe essere dato dal sito imgur, che carica l'immagine ? E' pur vero che quando prendo il caffè al bar lo zucchero ce lo devo mettere io….

Ad ogni modo, ora starò attento a completare, se vedo che il link non è completo. Allora vediamo se riesco a caricare correttamente una immagine , stavolta disegno una ellisse …..

Perfetto ! Ma lo zucchero ho dovuto metterlo io nel caffè !

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

introduzione alla geometria dello spazio - seconda parte **

Articoli correlati

Soluzione del "banale" esponente **

(Q) Un semplice esponente ... **

Soluzioni dello scontro evitato **/***

Evitiamo uno scontro **/***

16 commenti

Lascia un commento Cancel Reply

Soluzioni dello scontro evitato /*

Evitiamo uno scontro /*