Categorie: Articoli Matematica
Tags: geometria geometria dello spazio geometria solida ippopede di Proclo lemniscata Lemniscata di Bernoulli lemniscata di Booth ovali ovali di Cassini piano sezioni spiriche toro
Scritto da: Arturo Lorenzo
Commenti:0
Spiriche - Appendice 2 alla parte 8° sul toro ***
Sezioni spiriche, ippopede di Proclo, lemniscate
Rieccoci qui con l'ultima parte dell'appendice all'articolo 8° sulla geometria solida, dedicato al toro. Nella prima appendice abbiamo fatto la conoscenza delle circonferenze di Villarceau. In questa seconda appendice illustrerò altre interessanti curve ottenibili andando a sezionare il toro con un particolare piano. Ci serviremo, come sempre in geometria analitica dello spazio, del linguaggio della matematica. Ma niente paura, useremo strumenti semplici. E, in ogni caso, se avete dubbi, non avete che da chiedere nei commenti.
L'ultima volta avevo concluso l'articolo accennando alle sezioni spiriche, che sono proprio quelle di cui ci occupiamo questa volta. Intanto, perché si chiamano spiriche ? Come spesso accade, il termine deriva dal greco, per la precisione dalla parola σπειρα che in greco antico significa toro . E pare sia stato proprio un matematico greco antico , Perseo, ad avere scoperto le sezioni spiriche nel 150 a.C.
Ciò che le caratterizza è di essere ottenute sezionando il toro con un piano parallelo al suo asse di rotazione.
Fig.1 - Sezione di un toro con un piano parallelo all'asse di rotazione
L'ippopede di Proclo
Ormai sappiamo che, in geometria analitica, sezionare un solido con un piano equivale a mettere a sistema l'equazione del solido con quella del piano. Così faremo anche questa volta. Rammentiamo, dunque, l'equazione del toro di raggio maggiore R, raggio minore r, con asse di rotazione coincidente con l'asse z e centro nell'origine:
(1)
(chi non avesse letto il primo articolo di questa serie, in cui veniva ricavata la suddetta equazione, lo trova a questo link)
Consideriamo, ora, l'equazione del piano parallelo all'asse z e posto a distanza k dall'origine degli assi. Per semplicità, orientiamo la terna di assi cartesiani in maniera tale che l'asse y risulti perpendicolare al piano con cui stiamo andando a sezionare il toro. In tale sistema di riferimento, ricordando il concetto di luogo geometrico, tutti i punti del piano secante avranno coordinata y pari a k. In pratica, l'equazione del piano secante sarà
y=k (2)
A questo punto, potremmo mettere a sistema la (1) e la (2), per determinare l'equazione della curva di intersezione tra toro e piano nel sistema xyz. Ma, come abbiamo fatto già con le circonferenze di Villarceau, anche stavolta riferiamo l'equazione della curva cercata direttamente al piano a cui essa appartiene, in questo caso il piano di equazione y=k. Per fare questo dobbiamo passare dal sistema di riferimento originario O,x,y,z a quello traslato in direzione dell'asse y della quantità k. In pratica, l'asse y' del nuovo sistema di riferimento risulterà coincidente con quello y del sistema originario, mentre origine, asse x' e asse z', risulteranno semplicemente traslati lungo y della quantità k. Le equazioni per il passaggio dal primo al nuovo sistema di riferimento, quindi, sono:
x'=x
y'=y-k
z'=z
da cui, esplicitando rispetto a x, y e z, otteniamo:
x=x'
y=y'+k
z=z'
Andiamo, a questo punto, a sostituire le suddette tre espressioni trovate per x, y e z nella (1) e nella (2):
(3)
(4)
Sostituendo la (4) nella (3) ottengo:
cioè:
A questo punto, poiché sappiamo che x'=x e z'=z, possiamo riscrivere la suddetta equazione utilizzando direttamente la x e la z al posto di x' e z', quindi otteniamo:
(5)
Questa è l'equazione della curva di intersezione cercata, che si definisce ippopede di Proclo. Ippopede perché ricorda la forma del piede di cavallo e di Proclo perchè fu Proclo, un filosofo e matematico bizantino, il primo a studiarla nel V secolo dopo Cristo. Essa è una delle sezioni spiriche.
Se la osserviamo nel piano a cui essa appartiene (y=k), essa assume una forma differente a seconda della distanza k del piano secante dall'asse di rotazione del toro. Vediamo, allora, come essa varia al variare del parametro k.
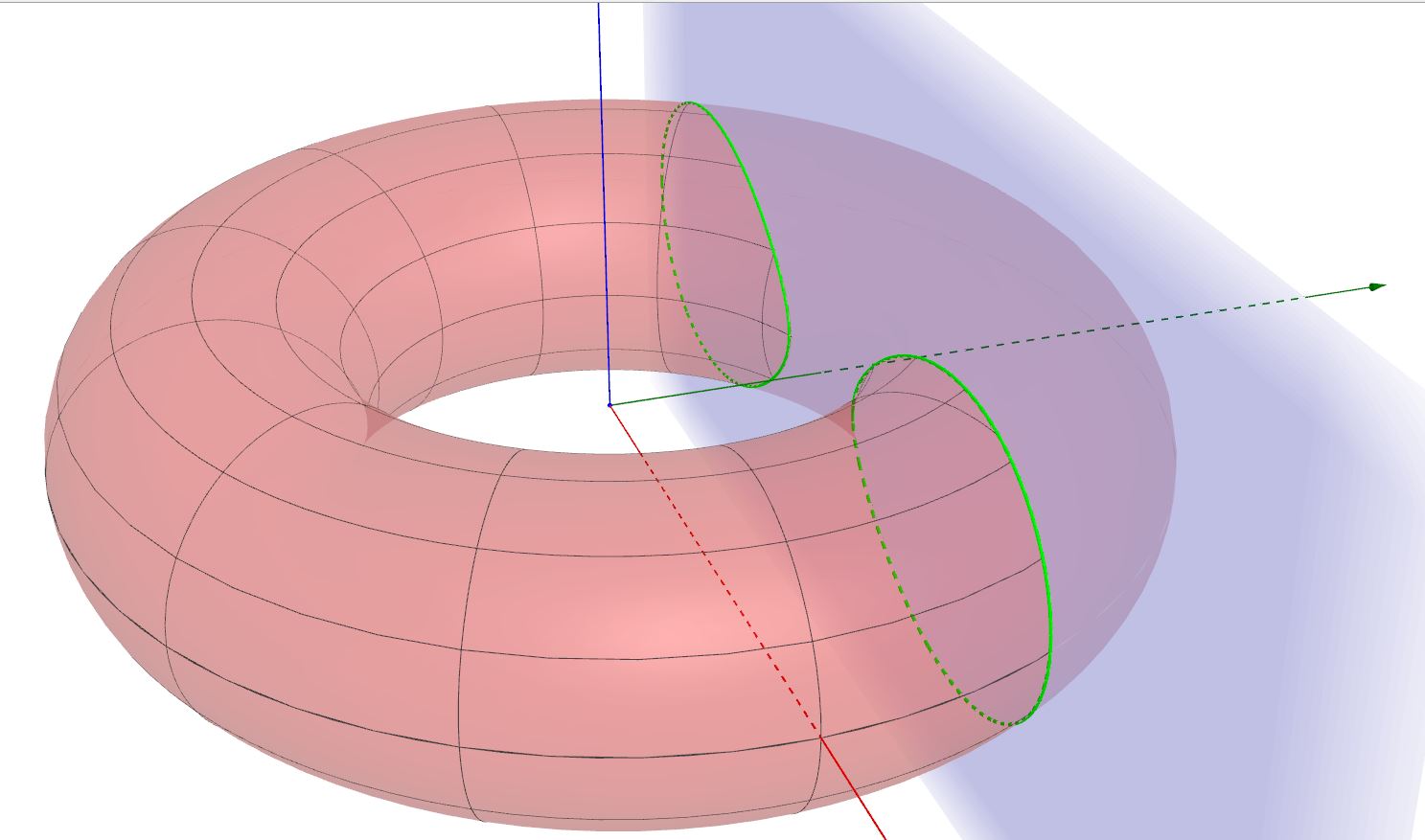
Cominciamo ad analizzare il caso in cui k=0, cioè il piano secante passa per l'origine:

In questo caso la (5) si semplifica in:
cioè:
E questa non è altro che l'equazione di due circonferenze in cui:
quindi con centro di coordinate
e raggio
Tali due circonferenze sono quelle colorate in verde nella figura n.2
Questo risultato era abbastanza intuitivo e prevedibile. Essendo, infatti, il toro generato dalla rotazione di una circonferenza di raggio r attorno ad un asse , se lo tagliamo con un piano passante per tale asse di rotazione non possiamo che ottenere due circonferenze di raggio r. Lo avevamo visto già nel primo articolo sul toro.
La lemniscata di Booth
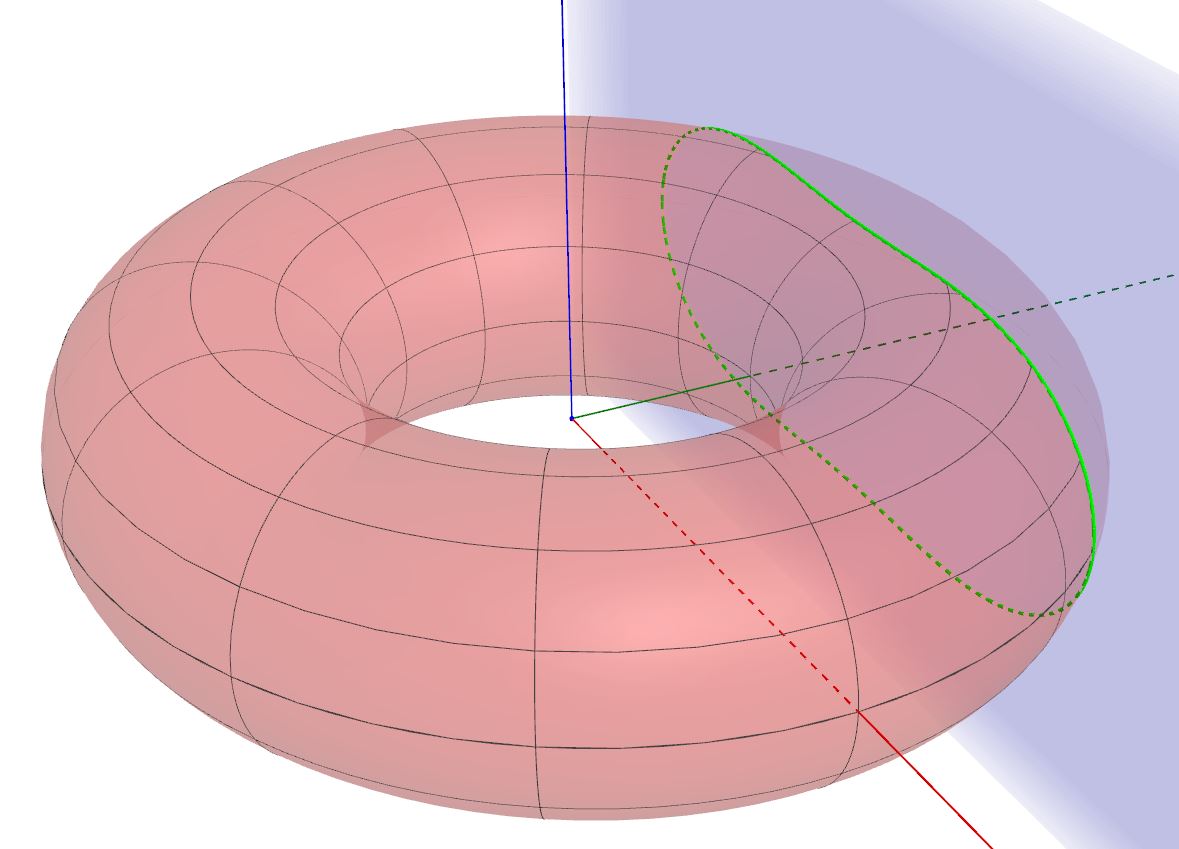
Cosa succede, invece, se poniamo k=R-r, cioè se rendiamo il piano secante anche tangente internamente al toro ? Consideriamo anche stavolta la seguente figura:

Come vedete, la curva di intersezione, sempre colorata di verde, diventa a forma di 8, è, quindi, una lemniscata, in particolare la si definisce lemniscata di Booth. Essa appartiene alla famiglia delle sezioni spiriche. Prende il suo nome dal matematico inglese James Booth che la studiò nel diciannovesimo secolo.
Determiniamone la rappresentazione analitica. Sostituiamo l'espressione k=R-r nella (5):
cioè, svolgendo i calcoli a primo membro:
(6)
Questa è l'equazione della lemniscata di Booth.
Per valori di k compresi tra 0 ed R-r , l'ippopede di Proclo assume una forma intermedia tra quella a due circonferenze e quella a lemniscata di Booth. Per valori di k maggiori di R-r e, naturalmente, minori di R+r (altrimenti il piano non interseca più il toro) , l'ippopede di Proclo assume una forma di ovale, come si vede dalla seguente figura:
Se k=R+r, cioè se il piano secante è tangente esternamente al toro, la curva di intersezione degenera in un punto.
La lemniscata di Bernoulli
Se, infine, il valore di R è pari al doppio di r (cioè R=2r) , e il piano secante è tangente internamente al toro, otteniamo proprio la lemniscata di Bernoulli.
Essa prende il nome dal matematico svizzero Jacques (o Jakob) Bernoulli, che la studiò nel diciassettesimo secolo.
Fu proprio Bernoulli a chiamarla lemniscata, dal termine latino lemniscus. Tale termine, presso gli antichi Romani, stava ad indicare il nastro che pendeva dalle corone.
A volere essere precisi, pare che 14 anni prima di Bernoulli, l'astronomo italiano Cassini avesse studiato una famiglia di curve chiamate, appunto, ovali di Cassini, di cui la lemnsicata è un caso particolare.
L'equazione della lemniscata di Bernoulli si ottiene sostituendo nella (6) ad R il valore 2r e svolgendo i calcoli :
(7)
che è proprio l'equazione cartesiana di una lemniscata di Bernoulli qualora si ponga:
(oppure a seconda dell'equazione che si vuole adottare per la lemniscata di Bernoulli. Alcuni testi riportano quella con il termine
, altri quella con il termine
).
Anche la lemniscata di Bernoulli appartiene alla famiglia delle sezioni spiriche.
Rammento che la lemniscata è una curva per i cui punti vale la condizione che il prodotto delle distanze dai due fuochi è costante. Se indico con F1 e F2 i fuochi della lemniscata di Bernoulli, essi hanno cordinate (-a,0) e (a,0), cioè, nel nostro caso
e
Effettivamente, se considero un qualsiasi punto della lemniscata di Bernoulli ottenuta sezionando il toro di raggio R=2r con un piano parallelo all'asse di rotazione e tangente internamente al toro, risulta che il prodotto della distanze di tale punto dai suddetti due fuochi è costante.
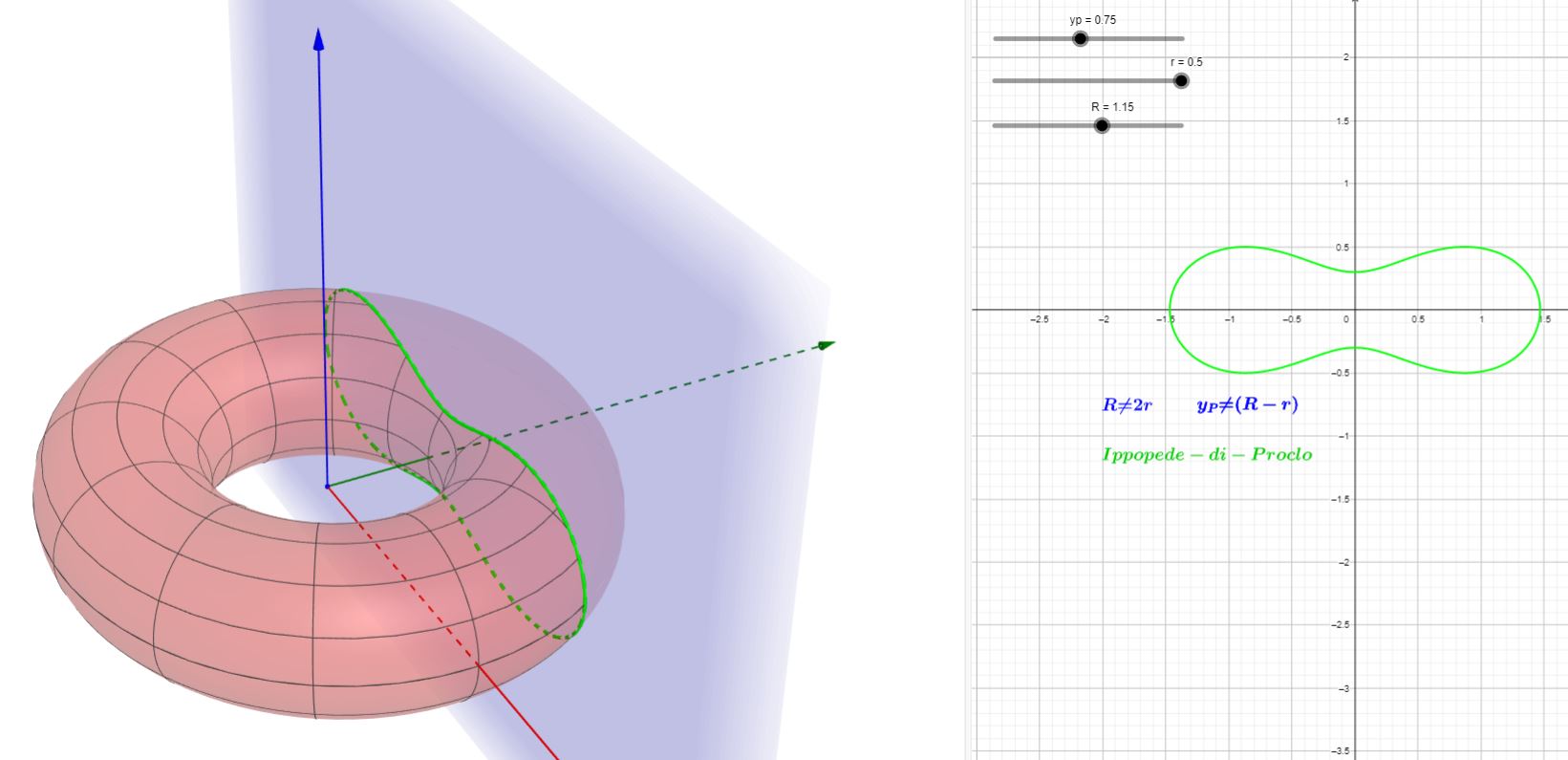
Evito il procedimento analitico e allego, invece, il modello interattivo da me realizzato con geogebra. Potete agire su esso in vari modi. Con l'apposito cursore per variazioni rapide o con i tasti freccia della tastiera per variazioni più fini, potete cambiare il valore di yp (che nel ragionamento sopra illustrato abbiamo "battezzato" con k), spostando così il piano secante nella direzione dell'asse y. In tal modo vedrete modificarsi, sia nella visualizzazione 3D che in quella piana a destra, la forma della curva di intersezione con il toro.
Se poi , agendo sui rispettivi cursori, variate i valori di R ed r in maniera che sia R=2r, quando tagliate il toro con il piano ad esso tangente internamente (yp=R-r) vedrete comparire in rosso la lemniscata di Bernoulli, con evidenziato un punto generico su di essa.
Spostando con il mouse tale punto, verificherete che il prodotto delle sue distanze dai due fuochi resta costante.
Sappiamo che la lemniscata è anche il simbolo a forma di 8 utilizzato in matematica per indicare un valore infinito. Bene, dal toro siamo andati a finire all'infinito. Sarà solo un caso ?... ![]()
---
Quelli che seguono sono i links a tutti gli articoli di geometria solida sinora pubblicati, prima di questo:
- Introduzione alla geometria dello spazio (parte prima)
- Introduzione alla geometria dello spazio (parte seconda)
- Introduzione alla geometria dello spazio (appendice)
- Geometria dello spazio (parte terza)
- Geometria dello spazio (parte quarta)
- Geometria dello spazio (parte quinta)
- Geometria dello spazio (parte sesta)
- Geometria dello spazio (parte settima - altri esempi di superfici di rotazione )
- Geometria dello spazio (parte ottava - il toro)
- Geometria dello spazio (parte nona - appendice 1 sul toro)
Li trovate anche nell'ARCHIVIO