Riprendiamo con questo  articolo il nostro viaggio nella geometria dello spazio. Nei precedenti articoli abbiamo discusso QUI di punti, rette e piani, nel riferimento cartesiano del piano e in quello dello spazio,  e QUI di fasci di rette e fasci di piani, oltre che di superficie sferica. Entità geometriche e concetti che ci sono serviti nell'appendice pubblicata QUI.

In questo articolo e in quello successivo intendo illustrare un elemento sinora da me mai citato ma che , come vedremo, si rivela molto utile nella trattazione di problemi di geometria, in particolare quella dello spazio. Tale elemento caratterizza una retta, indicandone la direzione, oppure un piano, consentendoci di individuarne subito tutte le infinite rette ad esso perpendicolari. Scopriremo che sia la retta sia il piano si "portano dietro" questo elemento come una targa identificativa, che a noi basta quasi leggere per conoscere subito, in termini analitici, la direzione della retta o la giacitura del piano.

Nell'articolo vengono citate entità vettoriali e operazioni tra vettori già bene illustrati nell'approfondimento che trovate QUI. Cercherò, comunque, ove lo riterrò opportuno, di facilitare il compito del lettore ripetendo in questa sede quanto già spiegato nell'approfondimento.

Intanto diamo un nome all'elemento oggetto di studio: "parametri direttori". A dire il vero, la denominazione non è universale. Su alcuni testi si parla di "numeri direttori", su altri di "coefficienti direttori". L'importante è , comunque, capirsi una volte per tutte e noi, a tale fine, in questo articolo e nei successivi useremo sempre e solo la denominazione di parametri direttori.

Cominciamo.

Parametri direttori di una retta nel piano

Sia data una retta r di equazione in forma implicita

ax+by+c=0

oppure in forma esplicita

y = mx + q.

Facciamo riferimento alla figura n.1

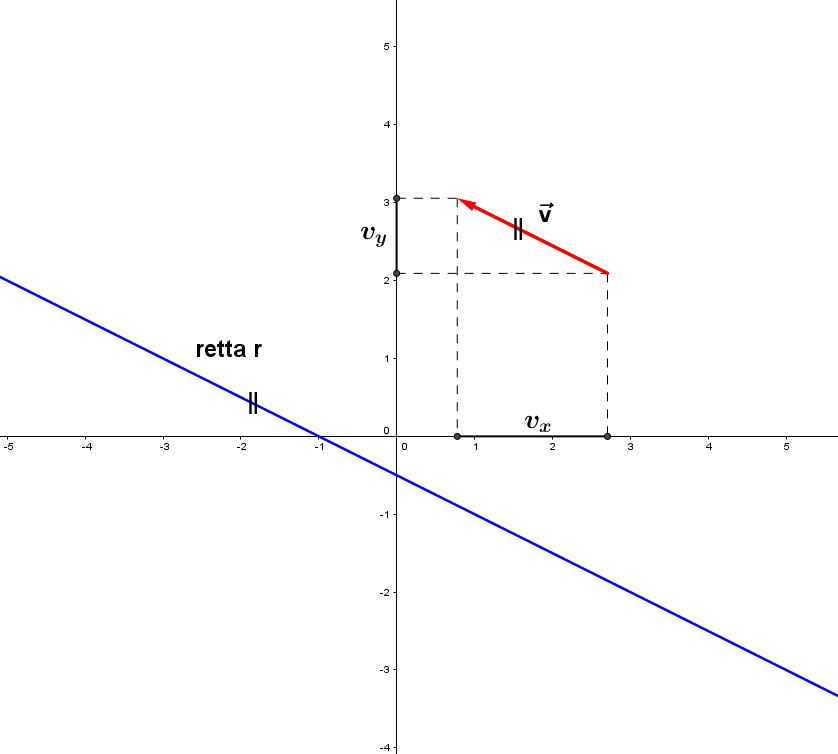
Si definiscono parametri direttori della retta le due componenti, secondo i due assi cartesiani, di un qualunque vettore parallelo alla retta. Sappiamo che le componenti di un vettore v , nel riferimento cartesiano del piano, sono i segmenti individuati dalla proiezione del vettore sui due assi cartesiani x e y. Chiamiamo con   e  tali due componenti, rispettivamente lungo l'asse x e lungo l'asse y. Se v è uno degli infiniti vettori paralleli alla retta r, allora   e  formano una delle infinite coppie di parametri direttori della retta. Ma come individuo, data la retta, una coppia di parametri direttori ? Nessuno impedisce di considerare , tra gli infiniti vettori paralleli alla retta r , quello che congiunge due qualsiasi punti A e B appartenenti alla retta r . In questo caso, infatti, il vettore v giace proprio sulla retta r, pertanto è banalmente ad essa parallelo. Facciamo riferimento alla figura n.2. Chiamiamo con  ,   e  ,  , rispettivamente, le coordinate cartesiane dei due punti.

 

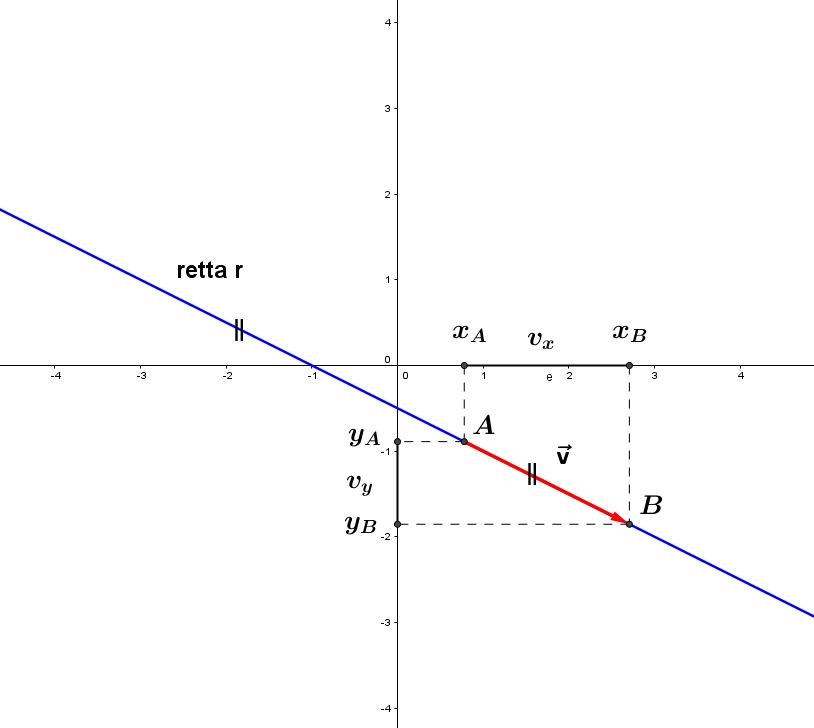
Le componenti di tale vettore sui due assi cartesiani sono (-) e (-) che, dunque possono essere prese come coppia di parametri direttori della retta. Ma intendo trovare tali parametri senza dover fare calcoli, semplicemente leggendo l'equazione della retta. A tale fine, continuiamo il ragionamento. Poiché i due punti A e B appartengono alla retta, le loro coordinate devono soddisfare l'equazione della retta. Ciò significa che se sostituisco tali coordinate alla x e alla y nell'equazione della retta ottengo una relazione vera. Cioè:

punto A:

punto B:

sottraendo membro a membro ottengo:

Questa relazione posso intenderla così: le differenze di coordinate (yb-ya) e (xb-xa) sono proporzionali ad a e (-b). Ma (yb-ya) e (xb-xa) abbiamo detto essere le componenti del vettore v (parallelo alla retta r) sui due assi cartesiani , quindi parametri direttori della retta. Pertanto, una coppia di parametri direttori della retta è data proprio da -b ed a, coefficienti che stanno lì a fare bella mostra di sé nell'equazione della retta stessa !

Facciamo un esempio per fissare bene i concetti.

Sia data la retta r di equazione 3x+2y+1=0 . In tale equazione , i coefficienti sono a=3 e b=2. Pertanto una coppia di parametri direttori di tale retta sarà (-2, 3) . Fatto ! Naturalmente, poiché moltiplicando un vettore per uno scalare, otteniamo un vettore parallelo a quello di partenza, possiamo ottenere infinite coppie di parametri direttori della stessa retta, moltiplicando la coppia prima trovata per uno stesso numero diverso da zero. Moltiplicando , per esempio, per (-1) otteniamo (2, -3). Anche questa è coppia di parametri direttori della retta r.

E se la retta fosse uno degli assi cartesiani ? Per esempio l'asse y, di equazione x=0. In tal caso a=1 e b=0. Quindi una coppia di parametri direttori dell'asse y è (0, 1). Analogamente, una coppia di parametri direttori dell'asse x è (1,0).

Sinora abbiamo ragionato riferendoci ad una retta di equazione in forma implicita.  Cambia qualcosa se, invece, la retta r ha equazione in forma esplicita y = mx+q ? Il ragionamento è identico, basta riscrivere l'equazione in forma implicita, partendo da quella data in forma esplicita:

mx-y+q=0

Ora i coefficienti sono a=m e b=-1. Pertanto una coppia di parametri direttori della retta sarà (1, m), anche questa immediatamente individuabile solo leggendo l'equazione della retta.

Vediamo ora casi di applicazione dei parametri direttori di una retta, più che altro per familiarizzare con essi.

 

Condizione di parallelismo tra due rette

Consideriamo due rette di equazione in forma implicita, rispettivamente

Trasformiamo le due suddette equazioni per renderle in forma esplicita:

r1:  

r2:

I coefficienti angolari delle due rette, sono dunque

Sappiamo dai precedenti articoli che due rette sono parallele se hanno lo stesso coefficiente angolare, cioè:

m1 = m2

Questa relazione, alla luce delle (***),  equivale a

-a1/b1 = -a2/b2

cioè

-b1/a1=-b2/a2

Questa è una relazione di proporzionalità tra i coefficienti delle equazioni delle due rette. Ma abbiamo visto prima che -b ed a sono i parametri direttori di una retta. Quindi si deduce che due rette sono tra loro parallele se i rispettivi parametri direttori sono tra loro proporzionali. Se le equazioni delle due rette sono scritte in forma esplicita è immediato confrontare i coefficienti angolari , quindi ci si sbriga prima per quella via. Se, invece, le equazioni sono scritte in forma implicita, allora basta confrontare i coefficienti omologhi delle due equazioni, senza fare alcun passaggio.

Esempio

Siano date le due rette di equazione, rispettivamente:

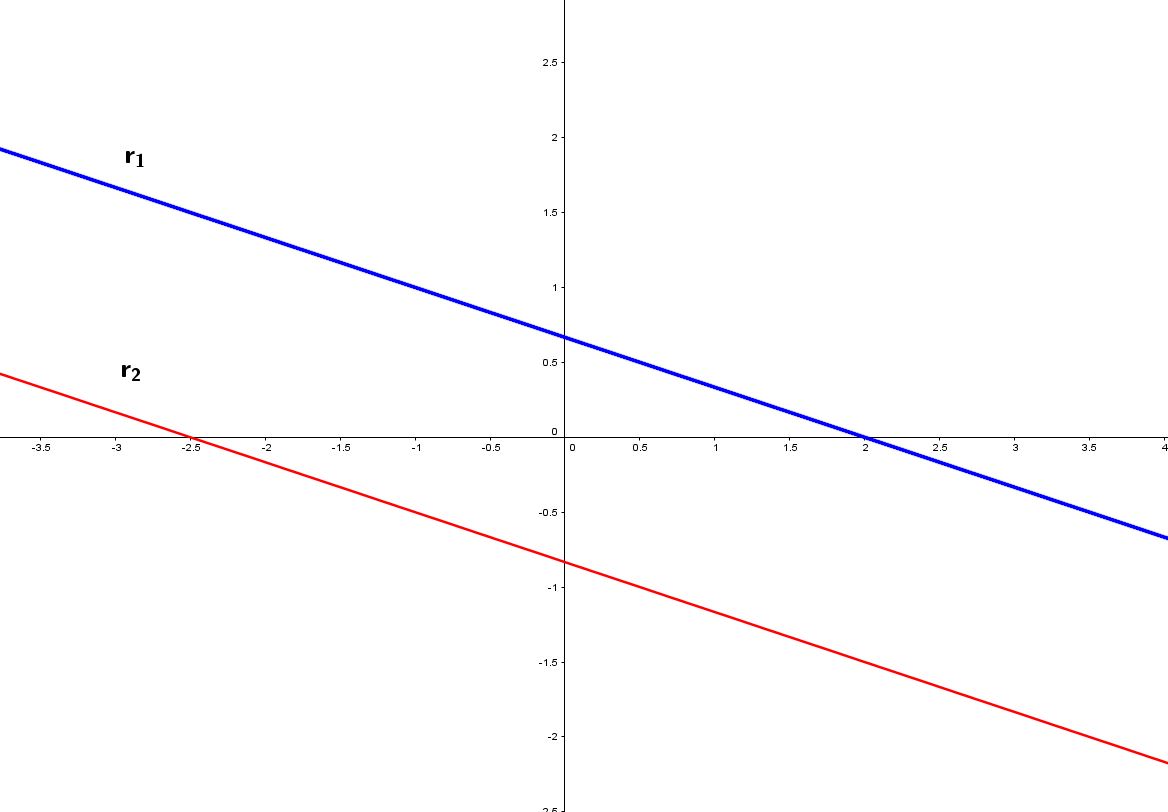
r1 : x+3y-2=0

r2 : -2x-6y-5=0

Confrontiamo i coefficienti a1= 1 e a2 = -2 , rapporto tra i due = -1/2. Confrontiamo i coefficienti b1=3 e b2=-6, rapporto tra i due = -1/2. I coefficienti della prima sono quindi proporzionali a quelli della seconda. Le due rette sono parallele. Fatto !

 

Condizione di perpendicolarità tra due rette

Consideriamo anche qui due rette di equazione in forma implicita, rispettivamente

Trasformiamo, come fatto prima, le due suddette equazioni per renderle in forma esplicita:

r1:  

r2:

I coefficienti angolari delle due rette, sono, al solito

Sappiamo dai precedenti articoli che due rette sono tra loro perpendicolari se tra i rispettivi coefficienti angolari vale la relazione:

m1 = -1/ m2

cioè, in base alle (***) :

-a1/b1 = b2/a2

che, portando tutto a primo membro, moltiplicando per -1 e facendo il minimo comune multiplo diventa:

      (*)

Questa relazione possiamo interpretarla come il prodotto scalare tra i vettori v(-b1, a1) e w(-b2, a2). Infatti, dal calcolo vettoriale sappiamo che il prodotto scalare tra due vettori è dato analiticamente dalla somma dei prodotti delle rispettive componenti. Ma allora, se , in base alla (*), tale prodotto scalare è nullo, significa che i due vettori (entrambi non nulli), sono tra loro perpendicolari. Infatti, in base alla definizione di prodotto scalare, se esso è nullo e i vettori sono non nulli, deve essere nullo il coseno dell'angolo compreso. E ciò si verifica , appunto, quando l'angolo compreso è di 90 gradi, cioè quando i due vettori sono tra loro perpendicolari.

In definitiva, se abbiamo le equazioni in forma implicita di due rette, per verificare che esse sono perpendicolari tra loro, basta verificare che valga la (*).

Anche in questo caso, se le equazioni delle due rette sono scritte in forma esplicita è immediato confrontare i coefficienti angolari , quindi ci si sbriga prima per quella via. Se, invece, le equazioni sono scritte in forma implicita, allora basta verificare la (*).

Esempio

Siano date le due rette di equazione, rispettivamente:

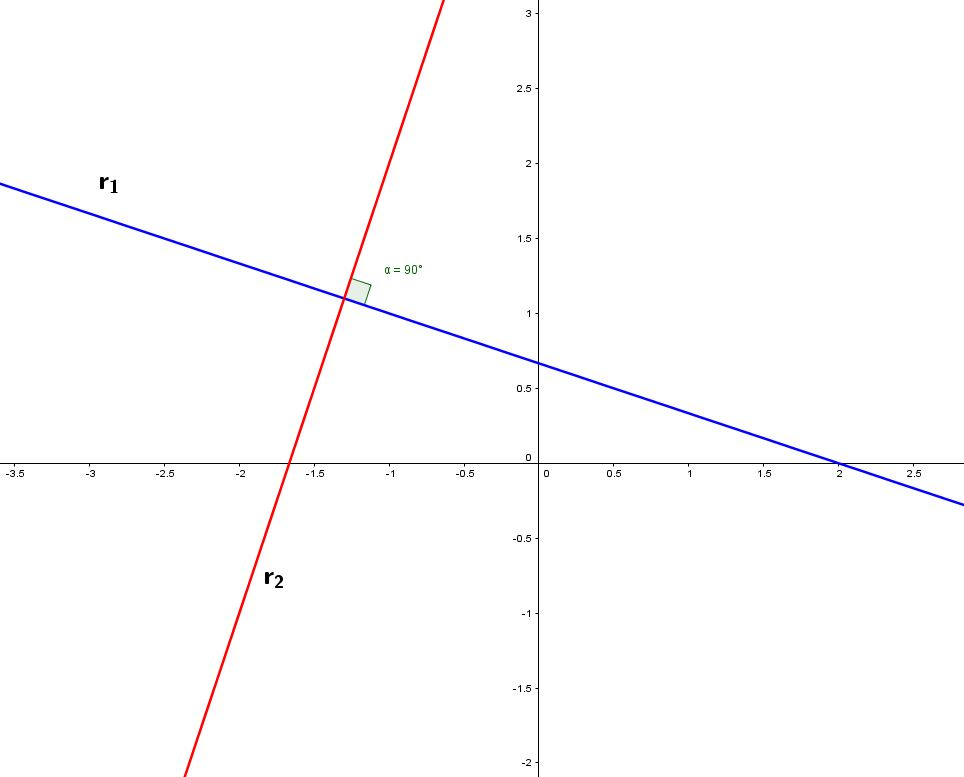
r1 : x+3y-2=0

r2 : -3x+y-5=0

Confrontiamo i coefficienti a1= 1 e a2 = -3,  b1=3 e b2=1. La quantità

a1a2+b1b2 = 1*(-3)+3*1=-3+3=0

Le due rette sono perpendicolari.

Nel prossimo articolo introdurrò i parametri direttori della retta nello spazio e del piano, per poi passare, nell'articolo ancora successivo, ad una loro applicazione entusiasmante, per i risvolti anche visivi e grafici : la costruzione di superfici di rotazione , ossia generate dalla rotazione di una data curva attorno ad un asse comunque inclinato nello spazio.