Categorie: Articoli Matematica
Tags: circonferenza fascio di piani geometria retta sfera
Scritto da: Arturo Lorenzo
Commenti:7
INTRODUZIONE ALLA GEOMETRIA DELLO SPAZIO - appendice
Dopo il primo articolo sulla geometria solida, pubblicato in due parti QUI e QUI nelle scorse settimane, eccoci ora giunti a questa appendice. In essa, mettendo in pratica i concetti di geometria solida sinora esposti, con particolare riferimento al piano, al fascio proprio di piani e alla sfera, dimostreremo che, dati due punti su una superficie sferica, la loro minima distanza, misurata sulla superficie sferica, è quella dell’arco di circonferenza massima passante per tali due punti.
Preciso che quella che espongo ora è "una" dimostrazione. Nel campo della matematica e della geometria esistono quasi sempre vie diverse per arrivare ad una stessa conclusione. Non escludo, quindi, che vi siano dimostrazioni alternative a questa. Essa va intesa più che altro come un esempio di applicazione di quanto visto nelle due parti del primo articolo sulla geometria solida.
Cominciamo, facendo riferimento alla figura n.1
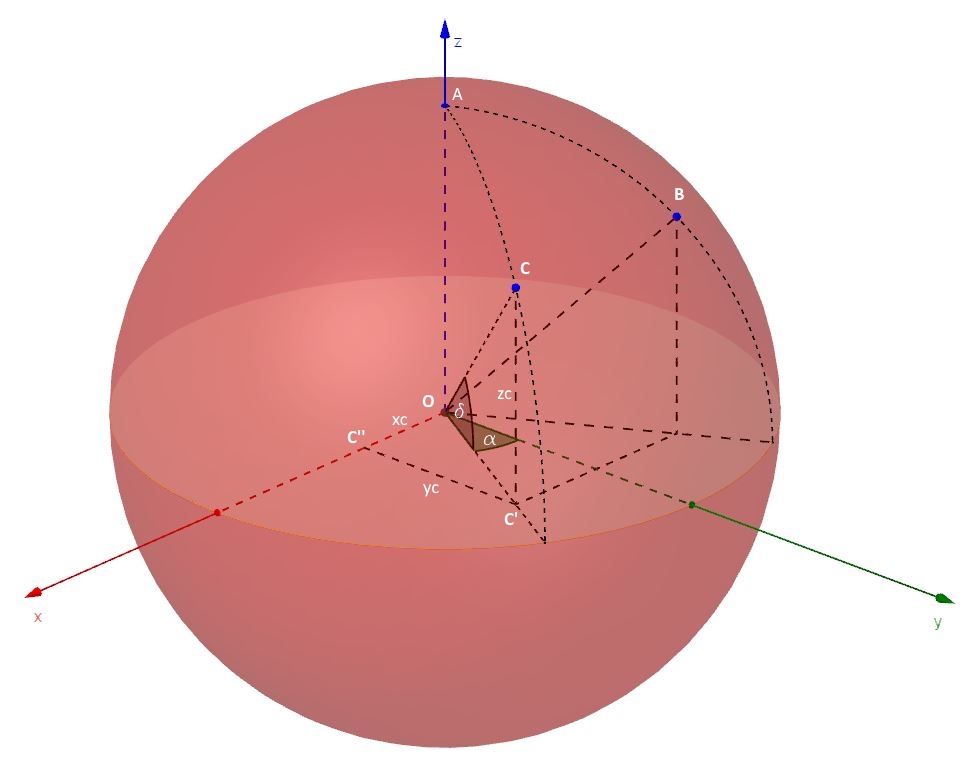
Per semplicità, ipotizziamo che i due punti B e C abbiano la stessa latitudine δ. Qualora avessero latitudine diversa, infatti, con una opportuna rotazione della sfera, si potrebbe sempre fare in modo di riportarci al caso, più semplice, di punti aventi uguale latitudine. I punti B e C siano, inoltre, separati longitudinalmente di un angolo pari a 2α. La superficie sferica a cui appartengono i due punti abbia raggio R e il centro sia coincidente con l’origine degli assi cartesiani x, y e z. In tale sistema di riferimento, dunque, l’equazione cartesiana della superficie sferica è :
Tra le coordinate cartesiane del punto C e gli angoli δ e α sopra definiti, si ricavano agevolmente le seguenti relazioni, considerando i triangoli rettangoli OCC’, rettangolo in C’, e OC’C’’, rettangolo in C’’:
Analogamente per il punto B, considerando il verso positivo dell’asse x, si ottiene:
Individuiamo ora la retta s dello spazio passante per i punti B e C. Nello spazio, una retta generica è individuata dalla intersezione di due piani. Nel caso che interessa, due piani “facili” la cui intersezione individua la retta s sono quelli indicati con e
nella figura n.2, il primo passante per i punti B e C e parallelo al piano cartesiano xOz, il secondo passante per i punti B e C e parallelo al piano cartesiano xOy.
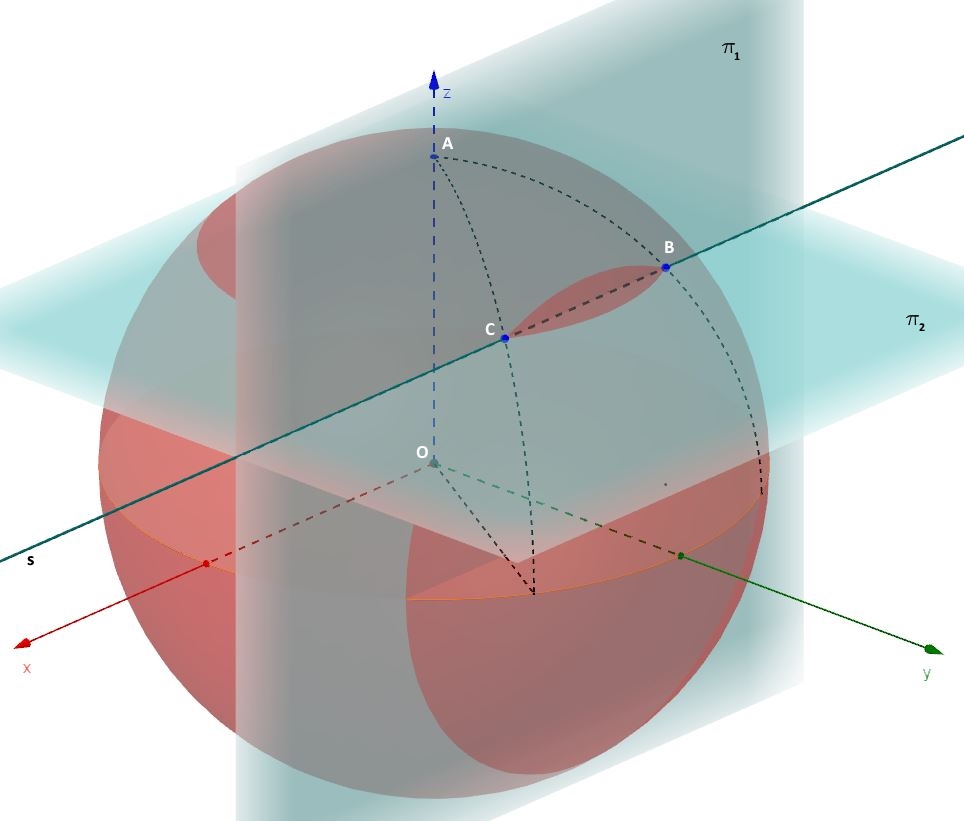
Il piano può essere visto come il luogo geometrico dei punti dello spazio aventi tutti la stessa coordinata y dei punti dati B e C, quindi la sua equazione cartesiana è immediatamente ricavabile:
cioè, sostituendo a l'espressione trovata prima:
(equazione del piano
)
Analogamente, il piano può essere visto come il luogo geometrico dei punti dello spazio aventi tutti la stessa coordinata z dei punti dati B e C, quindi la sua equazione sarà:
cioè, sostituendo a l'espressione trovata prima:
(equazione del piano
)
La retta s , in definitiva, è individuata nello spazio dal sistema di equazioni:
(sistema di equazioni della retta s)
Tutti i piani passanti per i punti B e C avranno la suddetta retta come sostegno. In pratica, apparterranno al fascio proprio di piani avente come sostegno la retta s. In altre parole, la retta s è quella attorno alla quale possiamo immaginare di ruotare un generico piano passante per i punti B e C, così da ottenere gli infiniti piani del fascio. Ciascuno di tali piani sezionerà la sfera e l’intersezione tra generico piano del fascio e la superficie sferica sarà una circonferenza di raggio r. Ricaviamo equazione del suddetto fascio proprio di piani. Essa si ricava considerando due degli infiniti piani appartenenti al fascio e facendone la combinazione lineare. Naturalmente, due piani li abbiamo già e sono proprio il piano e il piano
. Riscriviamo le rispettive equazioni come segue:
L’equazione del fascio proprio di piani avente per sostegno la retta s è dunque:
dove k è il parametro al variare del quale otteniamo tutti gli infiniti piani del fascio (con le precisazioni viste nei commenti alla seconda parte dell'articolo).
Possiamo riscrivere la suddetta equazione come segue:
(1)
Uno di tali piani del fascio è, per esempio, quello illustrato nella figura n.3 e indicato con il simbolo , con il pedice k proprio per indicare che esso dipende dal valore del parametro k. In tale figura è indicata anche la circonferenza
risultante dalla sezione della superficie sferica con il piano generico
.
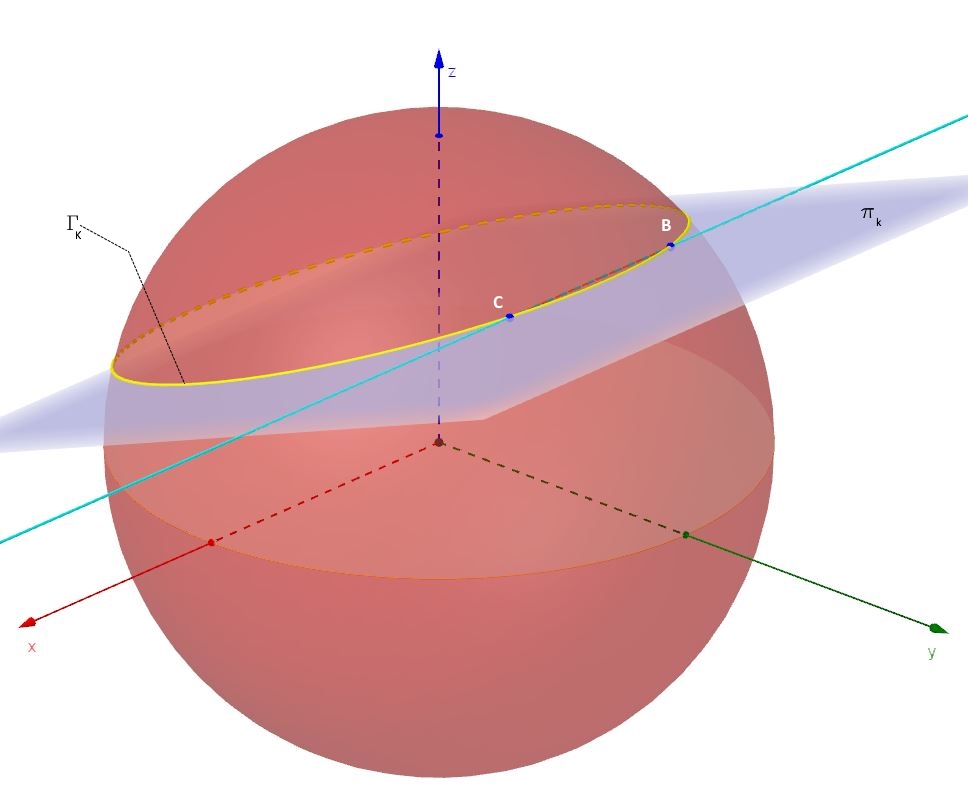
A questo punto si potrebbe pensare di mettere a sistema l’equazione del fascio di piani prima ottenuta con quella della superficie sferica, anche essa nota, per ricavare l’equazione della circonferenza generica. In tal modo, però, poiché le circonferenze ottenute sezionando la sfera con i piani del fascio giacciono su piani inclinati rispetto a quelli cartesiani, si incontrano notevoli complicazioni analitiche, a meno di non operare trasformazioni del sistema di riferimento per passare dai piani cartesiani al generico piano con cui si seziona la sfera.
Una alternativa sicuramente più agevole è quella di constatare che , qualunque piano del fascio si consideri per sezionare la superficie sferica, grazie alla simmetria spaziale di quest’ultima, si ottiene che la congiungente il centro della superficie sferica con il centro della generica circonferenza di sezione è perpendicolare al piano con cui si è sezionata la sfera. Ho illustrato tale circostanza nella figura n.4. Come spero si capisca dalla figura, il segmento ODk è perpendicolare al piano , per qualunque valore di k.
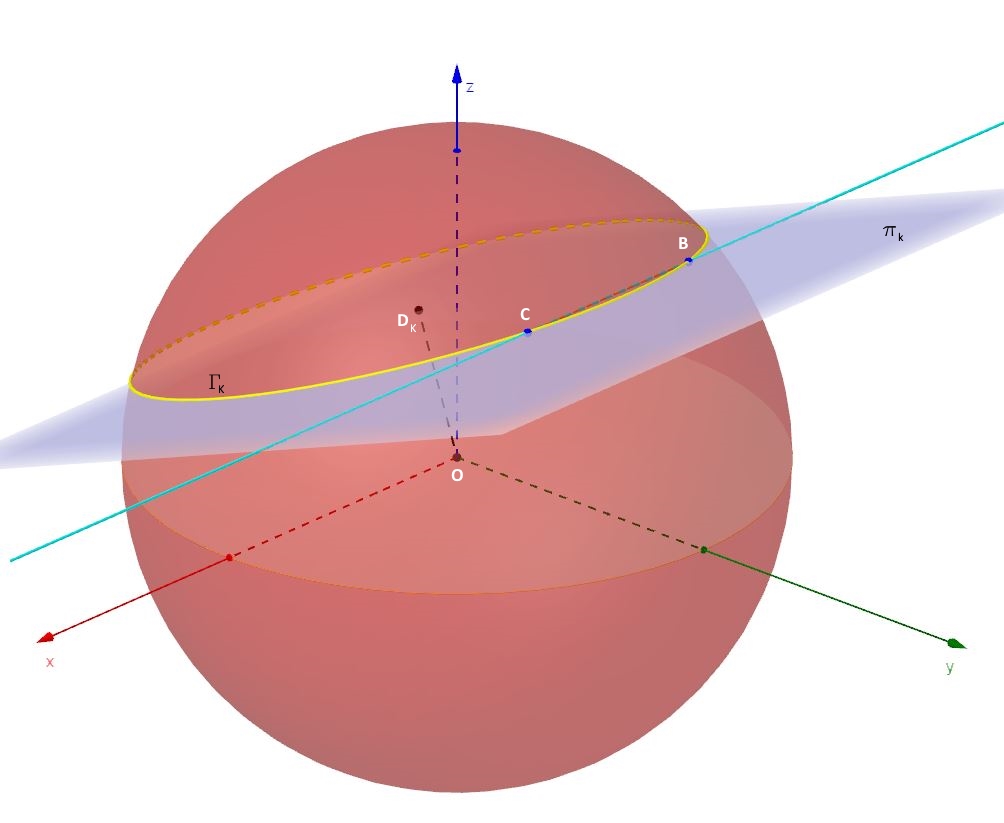
Ciò significa, per definizione di distanza in geometria, che il segmento ODk è proprio la distanza tra il centro O della superficie sferica e il piano su cui giace la generica circonferenza di sezione . Tale distanza ci è fornita dalla formula di geometria analitica dello spazio:
(2)
Dove a, b, c , d sono i coefficienti che compaiono nella equazione (1) del piano e
,
,
sono le coordinate del punto di cui si vuole calcolare la distanza dal piano. Nel nostro caso, considerando che il punto è l’origine degli assi cartesiani e facendo riferimento alla equazione del generico piano del fascio:
dalla (2) otteniamo:
Considero ora il triangolo OCDk, visibile nella figura n. 5, rettangolo in Dk. A noi serve conoscere r, cioè il raggio della circonferenza generica .
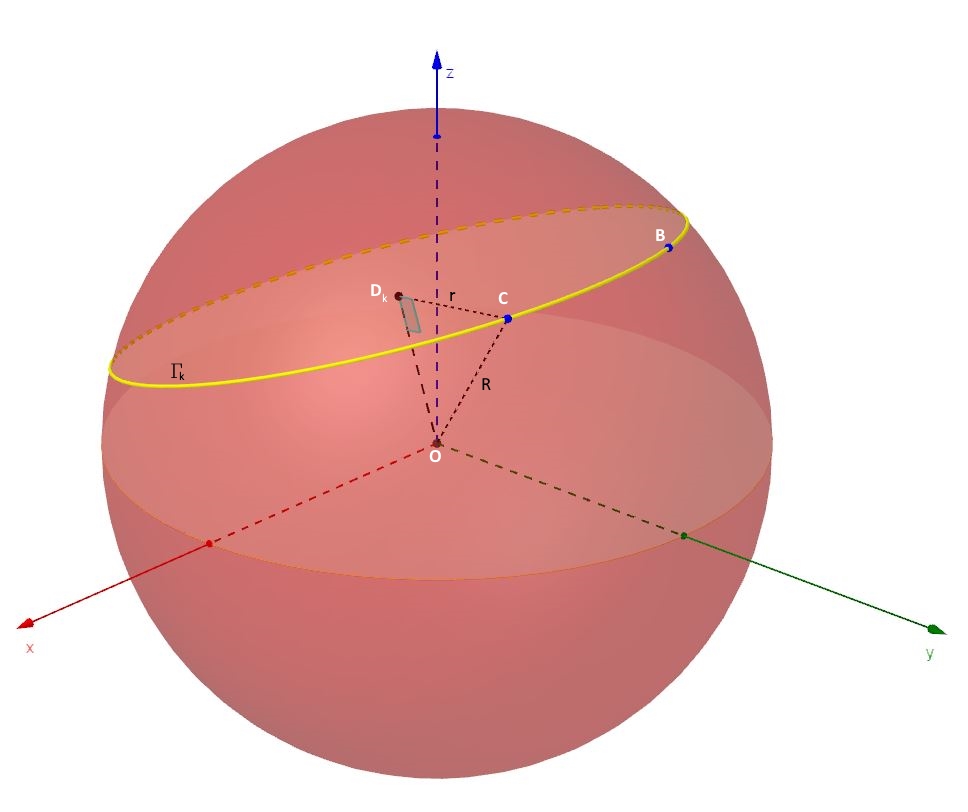
Applicando il teorema di Pitagora al suddetto triangolo rettangolo ricavo:
Ho in pratica ottenuto l’espressione del raggio r della circonferenza di sezione della superficie sferica con il generico piano
del fascio in funzione del parametro k.
Mi porto ora sul piano su cui giace la circonferenza di sezione e considero la figura n. 6
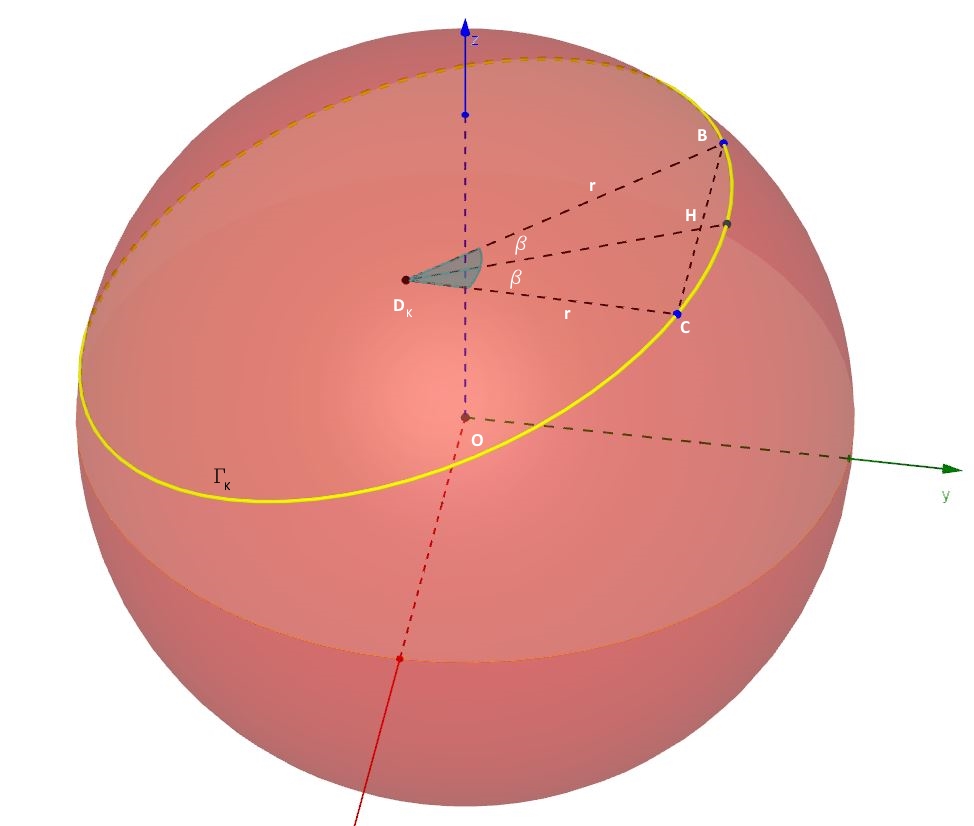
Considero il triangolo BCDk. Esso è isoscele, perché ha i due lati BDk e CDk uguali al raggio r della circonferenza di sezione . La base BC di tale triangolo isoscele è, quindi, data da:
da cui:
La lunghezza del segmento BC è nota essendo note le coordinate cartesiane dei punti B e C:
quindi:
A questo punto, posso finalmente ricavarmi la lunghezza dell’arco BC. Se in corrispondenza di 360 gradi ho la lunghezza di una circonferenza di raggio r pari a , in corrispondenza di un angolo 2β la lunghezza dell’arco di circonferenza sarà:
Non ci resta che sostituire nella precedente formula le espressioni precedentemente trovate per r e per β e ottenere:
(3)
Abbiamo così ottenuto l’espressione della lunghezza dell’arco BC al variare del parametro k. Tale parametro, in pratica, è da considerare come variabile indipendente, mentre le altre grandezze coinvolte (δ, α, R) vanno viste come coefficienti. In definitiva, il secondo membro della suddetta formula va interpretato come una funzione della variabile k. A questo punto, dovremmo andare a cercare eventuali punti di massimo e/o di minimo di tale funzione, imponendo che in tali punti si annulli la derivata prima. E’ evidente la complessità del calcolo della derivata prima di una siffatta funzione, in cui la variabile k compare al denominatore, sotto radice quadrate e in un arcoseno.
Ho, quindi, fatto ricorso ad una applicazione online (desmos) con cui ho ricavato direttamente il grafico di tale funzione, visibile nella figura n.7.

Con i seguenti valori dei coefficienti:
la funzione attinge il valore minimo per
Se ora andiamo a sostituire tale valore di k nella equazione (1) del fascio proprio di piani avente retta di sostegno la retta s , otteniamo:
Ma questa è l’equazione di un piano passante per i punti B e C e per l’origine. Basta infatti sostituire le coordinate dell’origine nella suddetta equazione per ottenere un’identità, il che significa che le coordinate dell’origine soddisfano l’equazione del piano, cioè che il piano passa per l’origine. Tale circostanza si verifica qualunque valore si attribuisca ai coefficienti e
. Cioè, in corrispondenza del minimo della funzione, a prescindere dai valori di
e
, si ottiene sempre un piano passante per l'origine degli assi, ossia per il centro della sfera. La circonferenza per cui è minima la distanza tra i punti B e C, misurata sulla superficie sferica, non può che avere, pertanto, il centro nell’origine, quindi è una circonferenza massima.






7 commenti
Scusa Arturo se ti chiedo un chiarimento sul grafico della funzione 3) che esprime la lunghezza dell'arco in funzione di k; a me non viene fuori così ma una funzione con asintoto orizzontale ( per k che tende a +/- infinito il limite è finito), anche se ammette lo stesso minimo ( anzi anche massimo). Ho provato anche con desmos (ho usato anche io gradi per gli angoli), ma non mi viene fuori il tuo grafico, che assomiglia più ad una parabola. (alla fine non cambia niente, anche nella mia il minimo è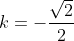 per alfa=45°,delta=45°).
per alfa=45°,delta=45°).
Caro Umberto, figurati, siamo qui tutti per chiedere chiarimenti ;-)
Con ogni probabilità hai ottenuto lo stesso grafico che ho ricavato con desmos, solo che io mi sono concentrato sul punto di minimo, facendo lo zoom del grafico intorno al valore di k per cui la funzione attinge appunto il valore minimo.
Se allargo la visualizzazione, in effetti viene fuori anche l'asintoto orizzontale. Questo è il link allo studio del grafico effettuato con desmos:
https://www.desmos.com/calculator/b8nlzia2ob
capisco; é lo zoom che mi ha tratto in inganno
Un ultima domanda sulla funzione (la parte geometrica è molto chiara)
Non riuscendo a studiare in nessun modo i minimi, a causa della complessità della derivata, ti sei appoggiato a desmos per calcolare il minimo della funzione graficamente nel caso alfa=45°, delta=45° e ottenendo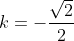 che sostituito nell'equazione del fascio, genera un piano passante per B, C e per il centro della sfera, che genera in tal modo come intersezione un cerchio massimo. Questo si vede sostituendo i valori. Ma mi sfugge il significato dell'ultima affermazione:
che sostituito nell'equazione del fascio, genera un piano passante per B, C e per il centro della sfera, che genera in tal modo come intersezione un cerchio massimo. Questo si vede sostituendo i valori. Ma mi sfugge il significato dell'ultima affermazione:
Tale circostanza si verifica qualunque valore si attribuisca ai coefficienti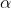 e
e 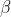 .
.
come possiamo dirlo in generale? Cioè che qualsiasi siano alfa,delta la funzione abbia sempre un minimo, e che tale minimo valore di k generi un piano che intersecato con la sfera dia un cerchio massimo?
Intanto grazie, Umberto, perché mi hai fatto accorgere di una svista che mi era sfuggita nella rilettura dell'articolo. Nella frase da te citata, infatti, i due angoli in questione sono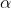 e
e 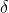 , non
, non 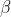 . Provvedo a correggere subito dopo avere scritto questo commento.
. Provvedo a correggere subito dopo avere scritto questo commento.
In merito alla tua domanda, è sicuramente legittima. Per avere certezza della generalità della conclusione, dovremmo dimostrare che il valore di k per cui si annulla la derivata prima della (3) è lo stesso per cui si ha un piano passante per i punti B, C e l'origine degli assi, a prescindere dai valori degli angoli suddetti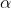 e
e 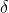 .
.
Ora, se considero l'equazione (1) del fascio di piani con sostegno la retta passante per i punti B e C, per avere il piano che passa anche per l'origine devo imporre che sia nullo il termine noto dell'equazione del fascio (come facciamo nella geometria piana a proposito di rette, circonferenze, parabole.. passanti per l'origine). Cioè deve essere:
da cui:
Se ora mi diverto a variare a piacimento i valori degli angoli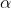 e
e 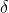 , mi accorgo che il valore di k risultante dalla suddetta equazione è esattamente lo stesso per cui si annulla la derivata della (3) (studiata tramite desmos) in corrispondenza degli stessi valori degli angoli. Non può essere un caso..
, mi accorgo che il valore di k risultante dalla suddetta equazione è esattamente lo stesso per cui si annulla la derivata della (3) (studiata tramite desmos) in corrispondenza degli stessi valori degli angoli. Non può essere un caso.. 
Sicuramente c'è un modo rigoroso per dimostrarlo formalmente, ma la complessità della espressione della derivata della (3) mi ha frenato dall'intraprendere quel cammino.
avevo notato che per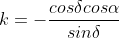 sostituendo nella formula del raggio si ottiene r=R; Purtroppo come dici tu nessuno è in grado di studiare quella funzione dal punto di vista dei minimi senza usare procedimenti grafici; scusa la mia pignoleria, si intuisce che quel valore dà un minimo, io però sono quasi convinto che è impossibile dimostrarlo formalmente per qualsiasi valore dei due parametri. L'unica cosa per me che si può dimostrare è l'esistenza del minimo (la funzione è continua,non è costante,ha due asintoti orizzontali,assume valori sopra e sotto l'asintoto) e anche del massimo.
sostituendo nella formula del raggio si ottiene r=R; Purtroppo come dici tu nessuno è in grado di studiare quella funzione dal punto di vista dei minimi senza usare procedimenti grafici; scusa la mia pignoleria, si intuisce che quel valore dà un minimo, io però sono quasi convinto che è impossibile dimostrarlo formalmente per qualsiasi valore dei due parametri. L'unica cosa per me che si può dimostrare è l'esistenza del minimo (la funzione è continua,non è costante,ha due asintoti orizzontali,assume valori sopra e sotto l'asintoto) e anche del massimo.
Vorrei precisare che , con riferimento alla derivata della (3), la sua espressione puo' essere determinata applicando le usuali regole di derivazione. Ma la (3) è talmente complicata che il calcolo della derivata induce molto facilmente ad errori. Chi volesse vedere l'espressione della derivata , che per i suddetti motivi evito di riportare direttamente qui, senza impelagarsi nel calcolo, può utilizzare ad esempio il sito www.wolframalpha.com/ (altamente sconsigliato agli studenti... )
)
Una volta determinata l'espressione della derivata della (3), imponendo che essa si annulli avremmo una equazione da cui tirare fuori i valori della variabile k che la soddisfano. Per via grafica possiamo dire che tali valori sono proprio quelli che vengono fuori dall'equazione
Infatti, se osserviamo il grafico della derivata della (3) (colore marrone) e la retta di equazione (**) (colore blu), visibili qui:
https://www.desmos.com/calculator/imgimmaiui (nei grafici leggere x come k)
notiamo che entrambi grafici intersecano l'asse delle k per lo stesso valore di k. Questo a prescindere dal valore dei due angoli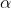 e
e 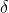 . Infatti, variando tale valore con gli appositi cursori visibili a sinistra del grafico, il grafico della derivata varia ma resta comune con la suddetta retta il punto in cui entrambi i grafici intersecano l'asse delle k.
. Infatti, variando tale valore con gli appositi cursori visibili a sinistra del grafico, il grafico della derivata varia ma resta comune con la suddetta retta il punto in cui entrambi i grafici intersecano l'asse delle k.