Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.

Grandezze fisiche

Per parlare di grandezze fisiche, proprio come il nostro amico Momento Angolare, è necessario dividerle, innanzitutto, in due grandi categorie, sulla base delle loro caratteristiche intrinseche, esprimibili con particolari notazioni matematiche.

Non spaventatevi di questa frase un po’ contorta, mi spiegherò velocemente. Prendiamo due grandezze tipiche della fisica, come la massa e la velocità. La prima è esprimibile con un numero, uno scalare, in una certo sistema di misura, ed è completamente individuata. Essa prende il nome di grandezza scalare. La seconda invece, ha bisogno di almeno tre caratteristiche per essere definita in modo univoco. Innanzitutto, un numero (che chiamiamo modulo) che ne indichi la grandezza (analogamente alle grandezze scalari), poi di una direzione e infine di un verso. La chiamiamo grandezza vettoriale.

In realtà, quando diciamo che una macchina viaggia a 100 km/h (grandezza di tipo scalare o modulo), dobbiamo anche indicare in quale direzione sta andando (sull’autostrada, sulla tangenziale, sul Corso principale, sul lungomare,…). La stessa velocità (come numero) può essere ottenuta su qualsiasi percorso e quindi va definito il percorso. Non basta ancora, però. Dobbiamo anche sapere se la macchina va dal centro verso il mare o in senso contrario. Si deve, quindi, aggiungere anche il verso di percorrenza. Spesso e volentieri, vi è anche bisogno di una quarta caratteristica: il punto di applicazione.  In altre parole, sappiamo che la velocità è di “tot” km/sec, che si sta ottenendo sulla strada che porta alla spiaggia e che va dal centro al mare, ma vogliamo anche sapere a che macchina si riferisce! Ci sono moltissime macchine che possono avere le stesse caratteristiche definite precedentemente.

Vi siete accorti che ho usato molte parole per descrivere questo tipo di grandezza fisica ed è sicuramente preferibile farci dare in prestito dalla matematica e dalla geometria una rappresentazione simbolica che unisca tutte e quattro le caratteristiche della velocità.

Questa rappresentazione simbolica si chiama vettore e le grandezze fisiche che ne fanno uso si chiamano grandezze vettoriali.  Lo possiamo applicare a un punto P che potrebbe essere un’entità fisica come ad esempio un corpo di massa m. Tuttavia, ripeto ancora, la grandezza scalare massa è del tutto estranea al vettore, al verso e alla intensità del movimento da lui indicato. Essa dipende solo dalla macchina, ossia -ancora meglio- definisce solo una caratteristica della macchina, qualcosa strettamente legata al suo peso.  Al limite, sarà trascinata, in modo “inerte”, dalla grandezza vettoriale. Riflettendo un attimo abbiamo già introdotto la quantità di moto… Ma, ci torneremo sopra a tempo debito.

Numeri e grandezze scalari

Prima di farci prendere per mano dai vettori, capiamo subito bene la differenza tra numero e grandezza scalare. Sembrano la stessa cosa, ma non lo sono… Una grandezza scalare è esprimibile con un numero, ma ha delle dimensioni in un certo sistema di misura. E’ una caratteristica fisica, esprimibile matematicamente con un semplice numero, ma non è un numero fine a se stesso. Se dico che una “pera” pesa 1 kg o che ha un volume di 100 cm³, conferisco all’oggetto "pera" una certa caratteristica (scalare). Se invece dicessi 5 pere, assocerei all’oggetto "pera" l’informazione relativa soltanto al numero di pere, senza stabilirne alcuna caratteristica intrinseca: potrebbero essere di massa diversa, di forma diversa, di volume diverso, ma non interesserebbe assolutamente. Rimarrei nel puro mondo della matematica: contare, sommare, moltiplicare numeri e nulla più. Invece della pera, ovviamente, potrei usare mele, scatole, stelle, elettroni, poco importa. Ogni grandezza scalare dona, invece, un’informazione in più su una certa entità fisica.

Sono grandezze scalari: la temperatura, la massa, la carica elettrica, la pressione, la densità, il volume, la lunghezza d’onda, la frequenza, il lavoro, ecc., ecc.

Sono, invece, grandezze vettoriali: la velocità, l’accelerazione, la forza, la quantità di moto, il momento angolare, il momento di una forza, il campo gravitazionale, ecc., ecc.

Disegniamo un vettore

Prima di applicare il vettore alle grandezze fisiche che ne hanno bisogno, descriviamolo molto accuratamente come entità puramente matematica. In Fig. 1 la retta indica la direzione, la freccia il verso, la lunghezza del segmento PR il modulo del vettore. Questa definizione è indipendente dalla grandezza fisica che andrà a rappresentare. Il punto P è il suo punto di applicazione. Attenzione al modo di scrivere un vettore. Esso lo indicheremo sempre con una lettera in grassetto (v). La stessa lettera, in corsivo, starà a indicare il modulo del vettore (v), ossia la sua parte numerica o -se preferite- la sua parte scalare. E’ una nostra scelta, seguita normalmente, molto utile per non confondere scalari con vettori.

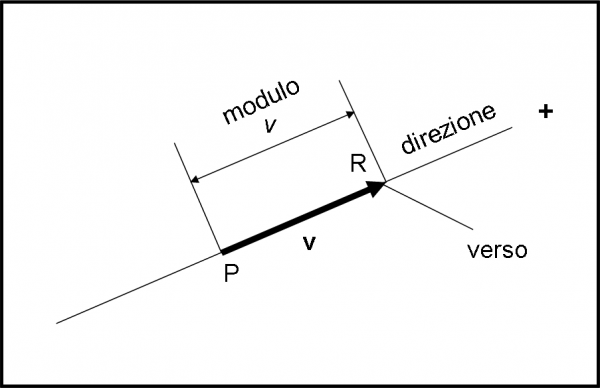
Operazioni tra grandezze 

Le grandezze scalari e vettoriali applicate agli oggetti dell’Universo permettono di descrivere le sue leggi e di capire come i vari attori stanno recitando. In poche parole, le grandezze fisiche, unite ai corpi materiali (ma non solo) a cui sono applicate, rappresentano la Fisica o, se preferite, l’Astrofisica.

Le grandezze vanno definite e capite molto bene, dato che ognuna di esse dice qualcosa di più sul corpo celeste. Senza conoscerle tutte (o quasi) diventerebbe impossibile stabilire che cosa è quel corpo e che cosa è in grado di fare o sta già facendo.

Le grandezze fisiche possono eseguire operazioni tra di loro ed è bene impararle perfettamente per poterle utilizzare normalmente quando ne avremo bisogno, così come abbiamo imparato le operazioni sui numeri in matematica.

Operazioni tra grandezze scalari

Ovviamente, anche le grandezze scalari sanno fare operazioni tra di loro e portare a drastici cambiamenti. Ma, essendo solo e soltanto dei numeri, le operazioni sono solo quelle che si applicano ai numeri, ossia ciò che noi abbiamo chiamato, molto semplicisticamente, matematica. Non c’è quindi bisogno di spiegare cosa permettono di fare. Ad esempio, se conosco la massa di un corpo e anche il suo volume, sono in grado di determinare una nuova grandezza (sempre scalare) che è la densità. Basta infatti dividere la massa per il volume e il gioco è fatto. Ribadisco ancora, in questo caso ho operato con grandezze fisiche scalari che sono rappresentate da numeri, ma che non sono numeri puri. Una massa di 5 (grammi) divisa per un volume di 2 (cm³) ci regala una densità di 2.5 (g/cm³), ma ogni grandezza ha la sua unità di misura, ossia identifica una ben definita caratteristica della materia. Se, invece divido una massa di 5 (grammi) per il numero 2 (fine a se stesso), non faccio altro che dividere a metà la massa : il risultato è solo e soltanto una massa dimezzata. So che sembrano sciocchezze, ma saper distinguere tra uno numero (matematica) e il numero che indica una grandezza scalare (fisica) è più che fondamentale nel mondo della fisica. E, prima o poi, ce ne accorgeremo…

In ogni modo, le operazioni svolte su grandezze scalari portano solo e soltanto a grandezze scalari.

Operazioni con le frecce: attenzione… possono pungere!

Le cose si complicano un poco, invece, quando si considerano le grandezze vettoriali. Esse possono agire insieme agli scalari oppure tra di loro.

Quando agiscono con uno scalare (che sia grandezza scalare oppure soltanto un  numero) hanno sempre il sopravvento. In parole semplicissime, se moltiplichiamo un vettore per un numero, il risultato è sempre un vettore. Il numero sarà solo in grado di aumentare la lunghezza o la grandezza del vettore (il suo modulo) o di incollargli un certa grandezza scalare, ma non di influenzare la direzione e il punto di applicazione. Il segno dello scalare (se lo consideriamo con segno) può indicare il verso del vettore. Se è positivo, il vettore non cambia verso, se è negativo, il verso è esattamente l’opposto di prima. Non tutti gli scalari hanno un segno (come la massa) e quindi non influenzano assolutamente né direzione né verso del vettore per cui sono moltiplicati.

Ripeto ancora: se, ad esempio, associo un grandezza scalare a un vettore, ottengo un nuovo vettore che ha un significato diverso. Ad esempio, la grandezza scalare massa moltiplicata per il vettore velocità da luogo nientedimeno che alla quantità di moto, uno dei capisaldi della meccanica classica (e non solo, come vedremo nell’atomo di Bohr). Se invece moltiplico il numero 3 per la velocità, ottengo un nuovo vettore velocità che rimane invariato tranne che per la sua lunghezza, pari a tre volte quella di partenza. Cambia il valore numerico della velocità, ma non cambia il tipo di grandezza vettoriale. Quest’ultimo caso lo vediamo in Fig. 2, per un numero positivo e uno negativo (3 e -3).

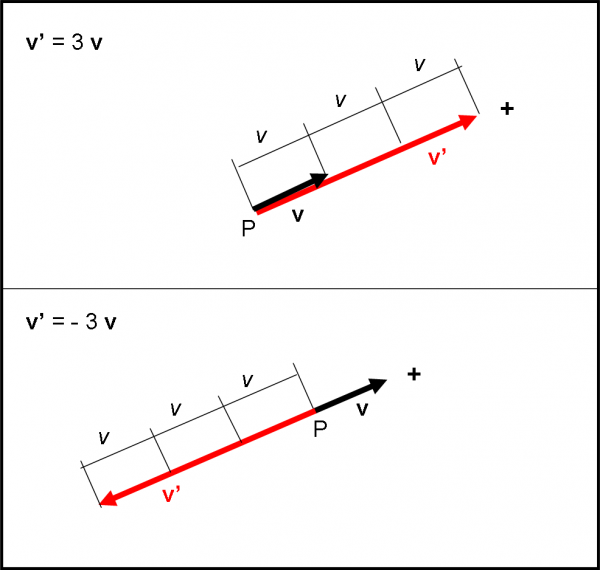
Riassumendo: se moltiplico (o divido) uno scalare per un vettore, lo scalare, che sia numero o grandezza scalare, entra tranquillamente all’interno del vettore e va a moltiplicare (o a dividere) solo il valore numerico del vettore (il modulo). Tra numeri si capiscono benissimo!

Il modulo del vettore prodotto tra scalare n e vettore v sarà dato da nv, mentre il vettore sarà indicato con nv. Se questo vettore fosse nuovamente moltiplicato per un’altra grandezza scalare m, otterremmo un vettore mnv, di modulo mnv.

Scomponiamo un vettore

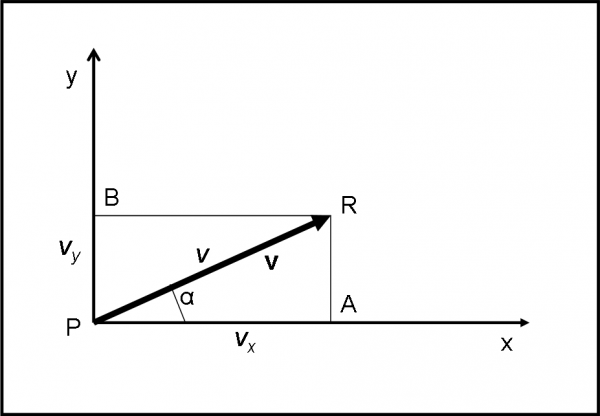
Prima di eseguire le operazioni tra vettori è bene imparare come un vettore possa essere scomposto su un piano cartesiano qualsiasi. Consideriamo, nella Fig. 3, un punto P e tracciamo gli assi x e y che hanno proprio origine in P (per comodità, dato che potrei usare qualsiasi tipo di assi cartesiani).

Se il punto P restasse fermo, potrei dire che non gli è associato nessun vettore. Sarebbe, però, molto meglio dire che gli è stato applicato un vettore nullo. Perché complicarci così la vita? presto detto: in Natura niente è mai veramente fermo e se un punto appare fermo (in un certo sistema di riferimento) vuol dire che agiscono più vettori su di lui, ma che, in qualche modo si abbracciano tra loro dando luogo a un vettore nullo. Pensateci bene sopra e vedrete che non ho detto assolutamente una cosa banale. Ho solo accennato all’equilibrio o -se preferite- alla statica…

Associamo a P (che potrebbe essere un corpo fisico  come una particella o una stella) il vettore v. Il suo modulo è v ed è proprio la lunghezza PR. La direzione è quella della retta PR e il verso è quello che va da P a R.

Occupiamoci, per un attimo, del vettore PR come se fosse un segmento del piano x,y. In altre parole, occupiamoci solo del suo modulo v. Come già detto, esso è dato dalla lunghezza del segmento PR. Sappiamo benissimo calcolare matematicamente le coordinate di un segmento rispetto a un sistema cartesiano (ripassate la matematica…). Tracciamo le perpendicolari dai punti estremi del segmento ai due assi. Otteniamo i due segmenti PA e PB.  Il primo, v_x, non è altro che la differenza tra le ascisse del segmento, ossia x_R-x_P, il secondo v_y è la differenza delle ordinate y_R-y_P. Quanto vale la lunghezza v del segmento PR? Conoscendo le due coordinate PA e PB è immediato ricavarla dal teorema di Pitagora:

v = (PA² + PB²)^1/2  = ((x_R-x_P)² + (y_R-y_P)²)^1/2 = (v_x² + v_y²)^1/2     …. (1)

Analogamente, potremmo anche legare le due coordinate PA e PB al modulo v, attraverso la trigonometria:

PA = v_x = v cos α

PB = v_y = v sen α     …..  (2)

Possiamo dire che conoscendo le coordinate del segmento, è immediato calcolare il modulo del vettore PR e viceversa.

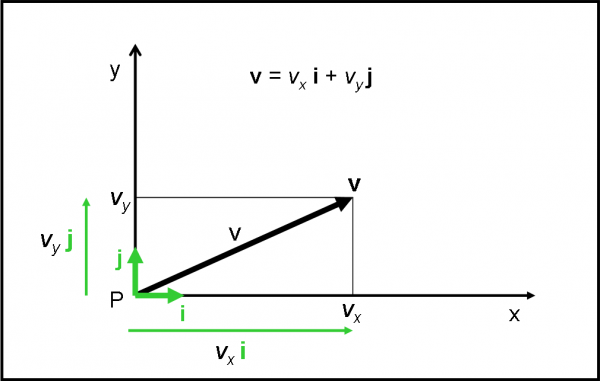
Aiutanti indispensabili: i versori

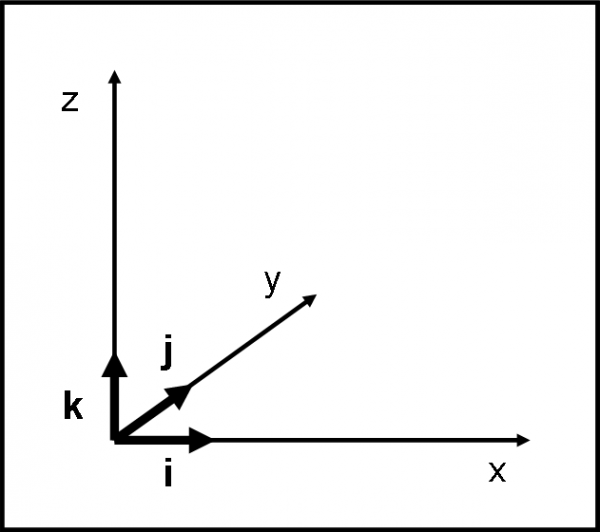
Potremmo anche ritenerci contenti. Però, è molto meglio introdurre due vettori  molto particolari che caratterizzino gli assi cartesiani x e y. Essi hanno come modulo il valore unitario (qualsiasi sia l’unità di misura che vogliamo assegnare alle coordinate), hanno la direzione degli assi e hanno il verso diretto verso destra (parte positiva dell’asse x ) e verso l’alto (parte positiva dell’asse y). Non hanno un punto di applicazione, dato che sono sempre disponibili, a seconda delle necessità del vettore che devono aiutare. Indichiamo con i quello relativo all’asse x e con j quello relativo all’asse y. Li chiamiamo versori degli assi coordinati. Per come sono stati definiti, i loro moduli saranno: i = 1, j = 1. Li vediamo nella Fig. 4.

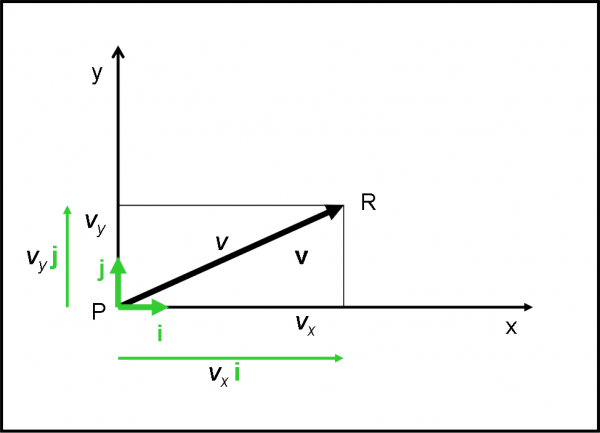
Da quanto abbiamo imparato nella moltiplicazione di un vettore per uno scalare, possiamo definire un vettore che sia il prodotto tra lo scalare v_x e il versore i. Scriviamo questo vettore come v_xi, di modulo v_x 1 = v_x. PB porta a un analogo vettore v_yj. Insomma, un vettore v può essere rappresentato molto bene da due vettori che utilizzino i versori i e j e le componenti lungo gli assi del modulo v.

Perché lo facciamo? Dato che ormai sappiamo come legare il modulo v di un vettore v con le coordinate v_x e v_y dei vettori v_xi e v_yj (attraverso le relazioni (1) e (2)), potremmo in ogni momento e per ogni vettore introdurre questi due vettori “ausiliari” scegliendo “ad hoc” gli assi cartesiani. L’importante è che i e j siano ortogonali tra loro. Abbiamo detto ben poco, ma il concetto è che esiste una relazione ben definita tra i moduli di questi tre vettori, che sfrutta il teorema di Pitagora e/o un minimo di trigonometria. Per il momento, abbandoniamo i versori e i vettori ausiliari. Li useremo tra poco…

Somma e differenza di vettori

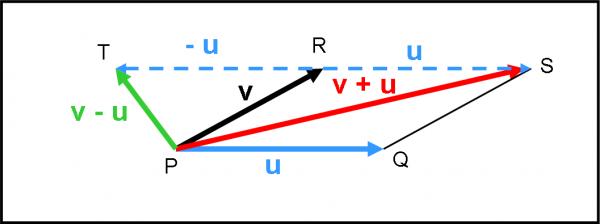
Occupiamoci, adesso, di definire la somma di due vettori, che per semplicità disegniamo entrambi con lo stesso punto di applicazione P. Il vettore PR (v) va sommato al vettore PQ (u).

Innanzitutto, dichiariamo apertamente che la somma di due vettori è ancora un vettore. Sappiamo già molto bene come si costruisce graficamente il vettore somma (perfino la QED ha usato questa operazione per sommare le ampiezze). In Fig. 5, basta traslare il vettore u fino alla “punta” del vettore v. Tracciamo poi il vettore che parte dal punto P e arriva al punto R, ossia che parte dalla “coda” di v e arriva alla “punta” di u. Non abbiamo fatto altro che usare la ben più celebre regola del parallelogramma. Il vettore somma lo chiamiamo w e vale la relazione:

w = v + u

Per ottenere la differenza dei vettori (v - u), basta ribaltare il vettore u e farlo diventare -u e poi eseguire la somma tra v e -u. Cosa già dette e ridetto varie volte.

Possiamo anche dedurre immediatamente che l'operazione "somma di vettori" è un'operazione commutativa, ossia:

u + v = v + u

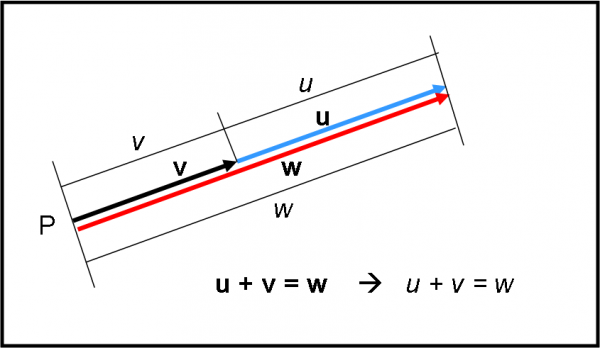
Graficamente, nessun problema, ma… quanto vale il modulo del nuovo vettore w = v + u?

Si potrebbe rispondere subito se i due vettori fossero  allineati (Fig. 6). La somma dei moduli dei due vettori sarebbe proprio uguale al modulo del vettore somma.  In altre parole, varrebbe anche:

w = v + u

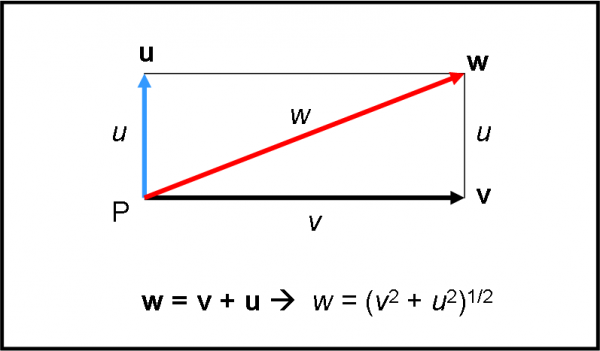
Attenzione, però. Questo è un caso estremamente particolare. In generale il modulo della somma NON è assolutamente uguale alla somma dei moduli. Si vede molto bene dalla regola del parallelogramma (Fig. 5). Il modulo della somma è la diagonale più lunga del parallelogramma. Sì, non sarebbe difficile determinare attraverso formule matematiche  la misura numerica della diagonale maggiore (o minore) di un rettangolo conoscendone i lati. Noi preferiamo farlo con quello che abbiamo appena introdotto, ossia attraverso i versori e i loro vettori ausiliari. Tornerà molto più utile e rapido (oltre che più … fisico). Per far ciò vediamo, prima, un altro caso particolare di somma di due vettori v e u.

Prendiamoli perpendicolari tra loro, come riportato in Fig. 7. Calcoliamone graficamente la somma, utilizzando le regole che abbiamo descritto precedentemente. Il vettore somma sarà w. Siamo di fronte a un rettangolo di lati u e v. La sua diagonale w si ricava immediatamente applicando il teorema di Pitagora. Ossia, otteniamo che:

w = (v² + u²)^1/2

Usiamo i versori

Abbiamo visto, però, che per ogni vettore v è possibile ottenere due vettori tra loro ortogonali che lo rappresentino lungo le direzioni degli assi cartesiani, facendo uso dei versori i e j. In altre parole, abbiamo la Fig. 8 (identica alla Fig. 4).

Per quanto abbiamo appena stabilito dalla Fig. 7, il vettore v è proprio la somma dei vettori v_xi e v_yj. Quindi possiamo scrivere:

v = v_xi + v_yj    …. (3)

la stessa cosa succederebbe se applicassimo in P il vettore u. Otterremmo nuovamente:

u = u_xi + u_yj   …. (4)

Ciò che abbiamo scritto è SICURAMENTE vero, dato che la somma di due vettori ortogonali come v_xi e v_yj è proprio v.

Utilizzando la (3) e la (4) possiamo, allora, scrivere, senza fare nessuna figura, la somma dei vettori u e v:

w = v + u = v_xi + v_yj + u_xi + u_yj = (v_x+u_x)i + (v_y + u_y)j = w_xi + w_yj

e, quindi:

w_x = v_x + u_x

w_y  =  v_y + u_y     …. (5)

Questa relazione ci dice una cosa importantissima:

Il vettore w, somma di due vettori u e v, può essere sempre rappresentato dalla somma di due vettori ortogonali (lungo due assi cartesiani scelti a piacere) che abbiano come modulo la somma dei moduli dei vettori v e u.

In breve: se conosciamo le componenti secondo due assi cartesiani qualsiasi dei vettori v e u, per ottenere le componenti del vettore somma basta sommare le componenti dei due vettori di partenza.

Abbiamo risolto il problema della somma di due (o più vettori) senza bisogno di fare una trattazione geometrica, ma utilizzando la scomposizione dei vettori lungo due assi cartesiani “comandati” dai versori i e j.

Potevamo farne a meno e risolvere il tutto con una bella figura. Tuttavia, questa descrizione ci permette di eseguire una scomposizione di un certo numero di vettori lungo due direzioni particolarmente interessanti (dal punto di vista fisico) e ottenere il modulo del vettore somma solo sommando i moduli dei vettori ottenuti dalla scomposizione. Chi volesse capire meglio questa motivazione, basta che pensi alla scomposizione dell’accelerazione di un corpo secondo due direzioni privilegiate, come quella tangenziale e normale alla traiettoria. In generale, quanto detto finora è già stato trattato (anche se un po’ diversamente) negli articoli sulla forza centrifuga. Questo (o quello) può essere un ripasso o una conferma…

Usiamo una semplice figura

Sapete, però, che, in fondo in fondo, sono una brava persona... Voglio, perciò, ottenere la stessa conclusione, utilizzando una rappresentazione grafica, sicuramente più intuitiva e immediata. Usiamo la Fig. 9, dove, nuovamente, vogliamo sommare i vettori v e u. Utilizziamo il metodo che trasla il secondo vettore e lo porta sulla “punta” del primo.

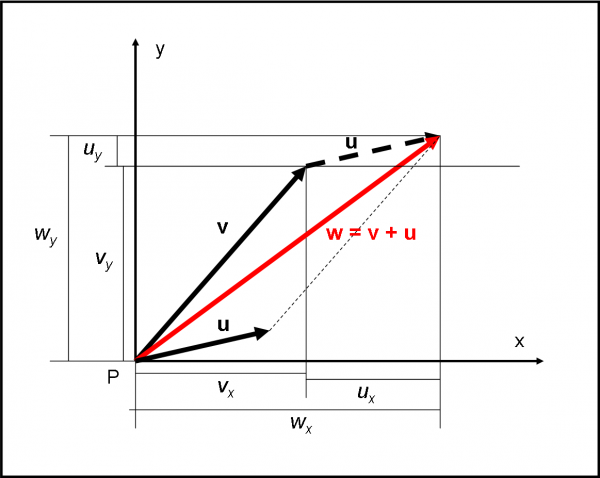
La figura mostra immediatamente che le due componenti w_x e w_y non sono altro che  (v_x + u_x) e (v_y + u_y).

Insomma, in un modo o nell’altro abbiamo risolto il problema di calcolare il modulo di un vettore che sia somma di due vettori. Usate quello che preferite, ma cercate di capirli bene tutti e due. Il primo è essenzialmente matematico e più generale; il secondo è essenzialmente geometrico e intuitivo.

Eseguiamo lo stesso calcolo nel caso di una differenza di vettori. Ovviamente le loro coordinate sono sempre le stesse, ossia:

v = v_xi + v_yj

e

u = u_xi + u_yj

Non ci resta che fare la differenza dei due vettori:

w = v - u = v_xi + v_yj - u_xi - u_yj = (v_x-u_x)i + (v_y - u_y)j = w_xi + w_yj

e, quindi:

w_x = v_x - u_x

w_y  =  v_y - u_y     …. (6)

Per trovare w, basta applicare, come sempre, il teorema di Pitagora:

w = (w_x² + w_y²)^1/2   …. (7)

I moduli sono ortogonali tra loro, proprio perché si riferiscono ai due versori ortogonali per costruzione. Posso tranquillamente applicare il teorema di Pitagora, come ho fatto sempre finora.

Ovviamente, si otteneva lo stesso risultato lavorando graficamente attraverso una Figura come la 9.

I versori, però, ci hanno permesso di usare solo semplici formule matematiche che possono applicarsi su un numero anche grande di vettori (magari sottraendone qualcuno e sommandone altri), senza dar luogo a una figura sempre più caotica e complicata…

In parole povere: se scomponiamo tutti i vettori che vogliamo sommare o sottrarre lungo degli assi cartesiani (uguali per tutti, ovviamente), ossia ricaviamo i moduli dei versori relativi a ciascun vettore, abbiamo ridotto tutto a una somma e/o differenza di moduli lungo il versore i e lungo il versore j. Il modulo finale di i e quello di j daranno le componenti del vettore finale.

Ad esempio:

v - u + t – s + z = w

si risolve trovando le coordinate di ogni singolo vettore e sommando quelle relative a i e quelle relative a j.

w = (v_xi + v_yj ) - (u_xi - u_yj) + (t_xi + t_yj) - (s_xi - s_yj) + (z_xi + z_yj)

Ho messo le parentesi per evidenziare i singoli vettori... scomposti (ma non ce n'era bisogno).

Raccogliendo i moduli di i e di j si ottengono subito le due componenti di w lungo i e j:

w = (v_x- u_x+ t_x - s_x+ z_x)i + (v_y - u_y+ t_y - s_y+ z_y)j

e, quindi:

w_x = v_x - u_x + t_x - s_x + z_x

w_y  =  v_y - u_y + t_y - s_y + z_y

Vi immaginate che caos sarebbe diventata la Fig. 9? E invece, in questo modo, abbiamo tutte le informazioni che vogliamo senza problemi. Una situazione del genere non è difficile da avere in fisica, quando su un certo oggetto agiscono molte forze o accelerazioni o velocità o qualsiasi tipo di grandezza vettoriale… e vogliamo trovare la grandezza vettoriale risultante. Ovviamente, non potrò sommare o sottrarre pere con mele, ma solo pere con pere e mele con mele…

Le operazioni tra scalari si riducono  una sola

Sembra quasi impossibile. Quando si parla di numeri, di “scalari”, le quattro operazioni fondamentali (che poi sono in realtà due dato che somma e differenza e prodotto e divisione sono praticamente la stessa cosa) si usano con pari frequenza e con difficoltà del tutto comparabili. Ed è abbastanza ovvio. Moltiplicare qualcosa vuol dire eseguire un certo numero di volte una somma, così come una divisione non è altro che eseguire un certo numero di volte una differenza. In altre parole, la somma (la differenza è una somma con segno invertito) ci permette di eseguire tutte e quattro le operazioni.

Ben diversa è invece la situazione per i vettori e, di conseguenza, per le grandezze vettoriali. Abbiamo già visto che la somma di vettori è qualcosa di banale, ma ha ben poco a che fare con la somma di due scalari. Coincide solo quando i vettori hanno la stessa direzione.

Se vi chiedessi: “Come si possono moltiplicare due vettori?”, qualcuno potrebbe pensare che è un po’ come per i scalari, ossia dovremmo sommare tante volte un vettore quanto ci dice l’altro… Che pasticcio… non avrebbe senso…. Insomma, non c’è niente da fare: scordatevi la relazione che c’è tra somma e prodotto nel mondo degli scalari e entrate senza rimpianti e senza idee preconcette nel mondo delle grandezze vettoriali. Lasciate anche alle spalle il prodotto di un vettore per uno scalare. Questa era ancora un’operazione legata al pensiero precedente: si prendeva il modulo del vettore (scalare), si moltiplicava per lo scalare (moltiplicazione “vecchio stampo”) e, solo dopo, il risultato veniva riconsegnato al vettore, che aveva solo guadagnato o perso qualcosa nella sua parte scalare.

L’abbiamo usata varie volte la volta scorsa, anche trafficando con i simpatici vettori unitari (i versori) e le componenti del vettore di partenza. Insomma, abbiamo solo scherzato… finora.

Il nuovo mondo, quello più usato nella meccanica classica, si mostra subito per quello che è: i prodotti tra vettori sono due, due operazioni completamente diverse tra loro. No, non siamo entrati nel Paese di Alice, siamo solo nel mondo delle grandezze vettoriali, quelle entità simboliche matematiche che hanno a loro disposizione tre armi diverse per combattere: modulo, direzione e verso, proprio come una spada!

Moltiplichiamo le spade

Non abbiate paura, vi capisco benissimo. Vi aspettereste che io scrivessi il prodotto di due vettori e vi dessi il risultato. Qualcosa del genere:

v u = ?

Mi spiace, non potrei proprio rispondere, perché quella scritta non ha alcun senso! Non ha assolutamente il significato di: “prendi il vettore v e sommalo a se stesso tante volte quanto dice il vettore u”. Anche perché cosa vorrebbe mai dire “tante volte quanto dice il vettore u” se u è un vettore che ha un modulo, una direzione e un verso? Lo potrei fare solo se u fosse uno scalare e allora ricadrei nel caso precedente: moltiplicherei il modulo di v per u e poi alla fine otterrei il vettore di modulo vu e di direzione e verso uguali a quelli di v.

Scusate se ripeto sempre le stesse cose e magari sembra che vi crei confusione. Normalmente, nessuno si cura di fare questi confronti e vi sbatte nel nuovo mondo senza nessuna preparazione mentale. Ne segue che i due mondi (scalare e vettoriale) sembrano due libri diversi e non due capitoli dello stesso libro. Sto solo dicendo cose ultra ovvie, che potrei cancellare tranquillamente, ma penso che il passaggio da operazioni tra scalari, tra scalari e vettori a quelle tra soli vettori abbiano bisogno di un certo intervallo di riflessione.

Adesso, però, può bastare e chiudiamoci la porta dietro, almeno per un po’.

La scrittura di sopra non ha senso, dato che non ha senso un’operazione indefinita tra due spade. Anche nella scherma esistono molti tipi di attacco e difesa. Nella simbologia delle grandezze vettoriali esistono solo due mosse: il prodotto scalare e il prodotto vettoriale. Li chiamiamo prodotti proprio perché hanno bisogno di un’azione reciproca delle due spade. Due attacchi o due difese o una parata e controparata, come preferite. Tuttavia, il concetto è sempre lo stesso: l’operazione prodotto indica un’azione da eseguire e comporta un certo tipo di risultato. Solo in questa definizione di massima si può vedere il ricordo delle operazioni tra scalari. Tuttavia, là si eseguivano solo degli “squallidi” conti, qui invece l’azione è variegata e complessa. Un po’ come una tenzone tra “villici” o tra “cavalieri”.

Fendente e tocco (prodotto scalare)

Devo ammettere che sono andato a documentarmi sulle azioni della scherma: il fendente è quel colpo che viene portato dall’alto in basso e che finisce col tocco. Direi che spiega abbastanza bene il primo prodotto vettoriale, quello scalare. Quel nome un po’ ambiguo (scalare) dà un po’ di fastidio, ma lo possiamo considerare come il risultato di un colpo vittorioso che annulla l’azione vettoriale e quindi conduce a una banale soluzione scalare. Basta! Vediamo di essere più seri.

Le due spade (forse per il fendente bisognerebbe dire sciabole, ma gli esperti mi scusino) sono il vettore v e il vettore u. Esse, in generale, fanno un angolo tra di loro, che chiamiamo ϑ, come mostrato in Fig. 10. Non stupitevi se le due spade vanno nello stesso verso… pensatelo come una fuga di chi subisce il colpo. La spada v cerca di colpire e cala il suo fendente verso la spada u. Quali sono i fendenti dei vettori? Presto detto: le sue coordinate, ossia le proiezioni lungo degli assi particolari. In questo caso l’asse scelto non può che essere l’altra spada (u). Cosa fa quindi il nostro vettore v? Costruisce la sua componente scalare, ossia la proiezione del suo modulo, proprio lungo la direzione del vettore u. La chiamiamo v_u, ed essa è, ovviamente, uno scalare. Usa il modulo, perché è il modulo che indica la “grandezza” (la violenza, in poche parole) per fare cadere brutalmente la componente sopra la direzione del vettore vittima.

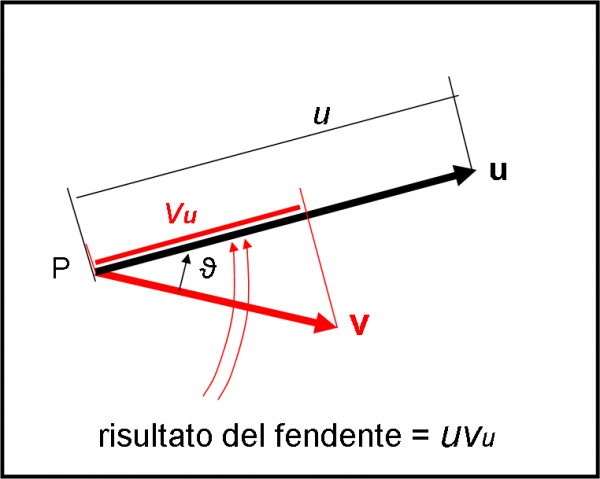
A questo punto v fa pesare la sua potenza d’azione, che viene quantificata dal prodotto (normale) tra la sua componente (il fendente) e il modulo u del vettore che ha subito il colpo. Insomma, in parole molto più serie: la sua componente moltiplicata per u. Per mantenere la nostra similitudine, potremmo dire che il fendente è quello che è, ma il risultato finale dipende da quanto è “grosso” l’avversario. Più è grosso e più il colpo è pesante e decisivo!

Forse qualcuno si sta stufando di questa trattazione puerile e fatta di ripetitive similitudini. Scusatemi, tra poco ripeterò le cose in modo più serioso. Il motivo è quello di cercare di offrivi un modo avventuroso e divertente per spiegare certi concetti ai più giovani, magari anche bambini. Non è mai troppo presto per capire cosa sono i vettori…

Possiamo definire l’azione che è stata svolta in un modo un po’ più fisico. Il vettore u ha una sua direzione e verso e quindi possiamo immaginarlo come un “trenino” che trasporta con sé il vettore v, attaccatogli in P. Tuttavia, siamo interessati solo alla parte del vettore v che si proietta sul treno u, ossia alla sua componente v_u. Più la componente è grande è più è grande il carico che mettiamo sul treno. Il risultato dell’azione svolta è il prodotto tra il modulo del … treno (u) e il carico parziale di v (la sua componente) inserito su di lui, v_u. Dato che uv_u è un prodotto normale tra scalari, potremmo anche dire che ci informa sulle condizioni finali del treno. Se  v_u fosse uguale a 1, avremmo il treno normale di partenza, ma dato che è stato moltiplicato brutalmente per un carico diverso da 1 (pari a v_u) il treno  deve faticare di più. Il risultato, comunque, è che il peso aggiunto comporta una fatica, un lavoro maggiore. Vedremo tra non molto quanto è azzeccata la parola lavoro.

Se queste parole in libertà vi hanno annoiato, dimenticatevele e riassumiamo “tecnicamente” cosa abbiamo fatto. Abbiamo costruito la componente v_u, del modulo v del vettore v, lungo la direzione di u e poi l’abbiamo moltiplicata per il modulo u del vettore u. Ossia, in termini matematici, il prodotto scalare dei due vettori v e u non è altro che la moltiplicazione delle due grandezze scalari v_u e u.

Abbiamo già capito perché si chiama prodotto scalare di due vettori: si parte da due vettori e si arriva a moltiplicare due scalari, il cui risultato è ancora uno scalare, ovviamente. Prima di scrivere per bene la formula che lo definisce, dobbiamo decidere che simbolo dare al prodotto scalare. Vi sono varie possibilità, basta mettersi d’accordo. Io preferisco rifarmi ai “miei” tempi e uso il simbolo x (il simbolo “antico” della moltiplicazione tra scalari), ma su internet e nei libri troverete anche altre simbologie. La formula che definisce il prodotto scalare (ossia il fendente tra due spade inclinate di un certo angolo tra loro) è, quindi, veramente semplice:

v x u = v_uu  … (8)        come già avevamo abbondantemente anticipato

Innanzitutto, troviamo quello che abbiamo detto fin dall’inizio: il prodotto scalare di due vettori è uno scalare ed è dato dal prodotto tra il modulo della componente del primo vettore, lungo la direzione del secondo, e il modulo del secondo.

Se vi sono sembrato troppo semplice, potrei velocemente complicare le cose e dirvi che il prodotto scalare è una trasformazione che associa a due elementi di un campo vettoriale un elemento di un campo scalare… Parole, parole, che noi possiamo benissimo tralasciare, ma non ci può sfuggire il fatto che usare il significato matematico più generale ci permetterebbe di entrare nelle teorie dei campi … ecc., ecc.

Torniamo alle nostre spade e cerchiamo di scrivere meglio la (8). Meglio abbondare e disegniamo la Fig. 11 che differisce ben poco rispetto alla Fig. 10.

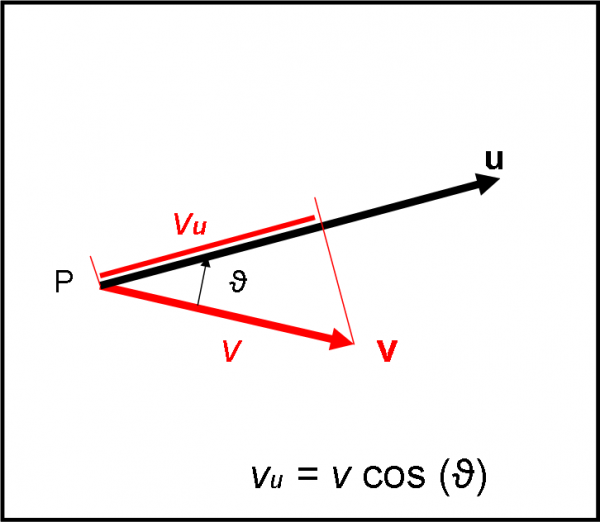
Siamo o non siamo in grado scrivere un po’ meglio la componente v_u? Direi proprio di sì, l’abbiano già fatto varie volte. In fondo, conosciamo l’angolo tra le due spade e quindi… basta usare quel poco di trigonometria che conosciamo:

v_u = v cos (ϑ)

e, quindi:

v x u = vu cos (ϑ)    …. (9)

In poche parole, il prodotto scalare di due vettori è il prodotto dei loro moduli moltiplicato per il coseno dell’angolo compreso.

Non sempre il fendente riesce

Continuiamo con la similitudine spadaccina… Se il vettore v sbaglia completamente il fendente e lo esegue nel verso opposto (Fig. 12) il risultato sarà un risultato davvero “negativo”. Infatti la sua componente v_u è relativa a un vettore v che va in verso opposto rispetto a u e quindi  l’angolo ϑ è ottuso. Ricordando che

cos (180 – ϑ) = - cos (ϑ)

il prodotto scalare risulta negativo. La formula da applicare è, comunque, sempre la stessa: ci pensa il coseno a darci il segno giusto.

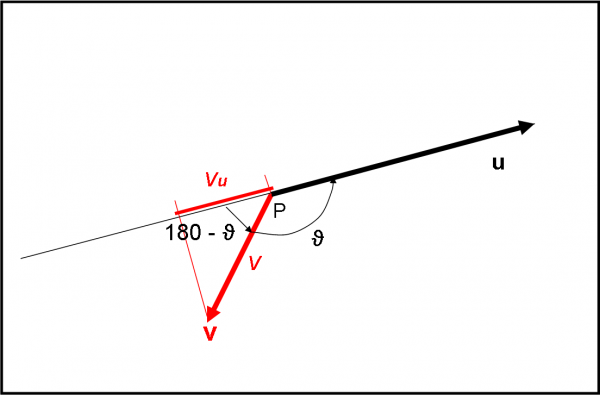
Non ci credete? Proviamo con un esempio .

ϑ = 60° ,   v = 2 ,    u = 5

v x u = vu cos (60°) = 2･ 5 ･ 0.5 = 5

ϑ = 120°,  v = 2 ,    u = 5

v x u = vu cos (120°) = vu cos (180°- 60°) =  - vu cos (60°) = - 2･ 5 ･ 0.5 = - 5

Per riallacciarci al caso del treno, potremmo dire che il carico non ben sistemato tende a far rallentare il treno e prima o poi cadrà. Tutta fatica inutile, un lavoro veramente negativo!

Ognuno può tirare il fendente

Il prodotto scalare è un’azione di scherma che non ha favoriti ed è del tutto reversibile. In altre parole, il risultato non cambia se l’azione viene svolta da u a scapito di v. Lo vediamo nella Fig. 13.

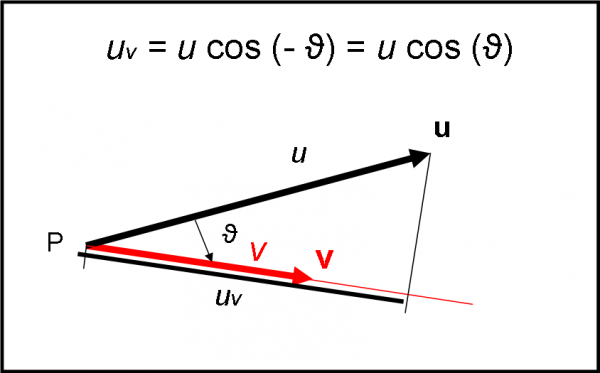
Possiamo benissimo costruire la componente di u lungo la direzione di v (è u che porta il fendente)  e calcolare il nuovo prodotto scalare, tenendo presente che l’angolo tra di loro rimane lo stesso, ma cambia di segno (ossia diventa – ϑ). Si ottiene:

u x v = u_vv = uv cos (- ϑ) = uv cos (ϑ)

Dobbiamo infatti ricordare che cos (- ϑ) = cos (ϑ).

Un risultato molto importante, dato che ci permette di scrivere:

u x v = v x u

Vale, perciò, la proprietà commutativa. Non è cosa tanto ovvia e banale, dato che il prossimo prodotto si comporterà in modo ben diverso… In termini schermistici, qualsiasi  dei due vettori tiri il fendente il risultato è esattamente lo stesso.

Sì, lo so, l’ho fatta lunga, ma penso che i vettori meritino un trattamento di favore. Il prodotto scalare non si troverà molto spesso in fisica, ma sicuramente è fondamentale quando si definisce il lavoro di una forza. Anzi, il lavoro è proprio il prodotto scalare di due vettori: la forza che agisce su un punto (o un corpo) e lo spostamento del punto (o del corpo). Pensateci e, prima o poi, ne parleremo.

Spade incrociate o allineate

Mi soffermo, invece, ancora un po’ sull’utilità del prodotto scalare nel definire la direzione reciproca di due vettori. Riscriviamo il nostro prodotto :

v x u = vu cos (ϑ)

Quando questo prodotto diventa uguale a zero? Beh, ci sono solo tre modi per ottenerlo: o va a zero il primo vettore o va a zero il secondo vettore oppure va a zero il coseno. Ovviamente, noi consideriamo vettori non nulli (che spade sarebbero?) e non ci rimane che porre il coseno uguale a zero.

Ma, per quali angoli va a zero il coseno? Presto detto solo per 90° o 270°, ossia per vettori perpendicolari tra loro (a parte il verso). Quindi, possiamo dire che due vettori sono perpendicolari solo e soltanto se il loro prodotto scalare è uguale a zero. E’ vero anche il viceversa, ma spesso si usa il prodotto scalare proprio per risalire alla direzione dei vettori.

Cosa succede, invece, se i due vettori sono paralleli tra loro? Beh… l’angolo diventa 0° (o 180°) e il coseno proprio 1  (o -1). Il prodotto diventa un valore massimo (o minimo) uguale al prodotto dei moduli (uv).

Se, inoltre, i due vettori fossero proprio uguali tra loro (stessa direzione, stesso verso e stesso modulo), l’ultimo caso darebbe proprio il quadrato del modulo del vettore (vu = vv = v²). In parole schermistiche: se le spade restano perpendicolari vi è un nulla di fatto; se una spada va completamente lungo la direzione dell’avversario si ottiene una poderosa botta dritta.

Versori e componenti lungo gli assi cartesiani

L’utilizzo di vettori uguali tra loro, ci fa tornare in mente i versori i e j. Per “piccoli” che siano sono pur sempre vettori! Sapreste dirmi quanto valgono i loro prodotti scalari, ossia:

i x j =

j x j =

i x i =

j x j =

Pensateci un attimo, prima di proseguire… dato che ho bisogno del risultato per la parte successiva. Avete risposto? Bene… allora sapete che

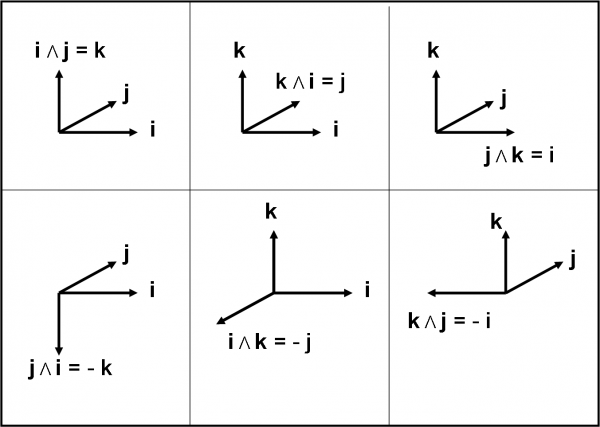
i x j = j x i = 0

i x i = j x j = 1

A questo punto inserisco la parte più “complicata”, che potete anche saltare, ma che è giusto inserire per gentilezza verso i nostri amici versori. In altre parole, vogliamo calcolare il prodotto scalare di due vettori, attraverso le loro componenti lungo i due assi cartesiani x e y. Dobbiamo farci, ovviamente, aiutare dai due versori degli assi cartesiani, i e j.

Come sappiamo dalla volta scorsa , possiamo scrivere il vettore v come

v = v_x i + v_y j

e quello u come:

u = u_x i + u_y j

Il prodotto scalare diventa:

v x u = (v_x i + v_y j) x (u_x i + u_y j) = v_xu_x i x i + v_x u_y i x j + v_y u_x j x i + v_y u_y j x j         …. (10)

Tuttavia, sappiamo che:

i x i = 1

i x j = 0

j x i = 0

j x j = 1

Basta sostituire e la (10) diventa:

v x u = v_xu_x + v_y u_y    …. (11)

in altre parole: il prodotto scalare di due vettori è dato dalla somma dei prodotti (normali…) tra le rispettive componenti (scalari) sugli assi cartesiani.

Evviva lo spazio

Prima di fare il passo successivo (sicuramente un po’ più impegnativo), lascatemi introdurre la terza dimensione, ossia l’asse z, perpendicolare al piano xy. Purtroppo, il prossimo prodotto, benché eseguito su un piano, ha bisogno della terza dimensione… Tanto vale allora, utilizzarla già adesso e riscrivere la relazione (10) nello spazio a tre dimensioni, dove un vettore ha ora tre coordinate: v_x, v_y e v_z. Essa diventa (non è certo difficile ottenerla):

u x v = v_xu_x + v_y u_y+ v_z u_z   …. (12)

Non sto a fare i conti completi, basta solo ricordare che, se k è il versore relativo all’asse z, avremo:

i x k = 0

j x k = 0

k x k = 1

Dato che l’asse z è perpendicolare sia all’asse x che all’asse y.

Bene, scusate le digressioni sulla scherma e poi gli affondi più impegnativi. Ho cercato di eseguire una trattazione che vada bene un po’ per tutti, dai neofiti ai più esperti. Ognuno, a modo suo, dovrebbe avere compreso il significato di prodotto scalare di vettori.

Non ci resta, adesso, che passare alla “presa di ferro” o a qualcosa di simile…

Un'azione dinamica: il prodotto vettoriale

Il prodotto scalare che abbiamo descritto nell’articolo precedente può essere considerato un’azione “statica”. Mi spiego meglio. Abbiamo proiettato un vettore su un altro (come se avessimo tirato un fendente) e poi ci siamo limitati a valutare il punteggio finale, ossia il prodotto tra la proiezione del primo vettore (componente) e il modulo del secondo. Un colpo e via! Non per niente il risultato è stata una grandezza scalare.

I vettori, però, sono grandezze dinamiche, in cui la direzione e il verso (la punta della freccia) indicano una propensione al movimento. Nel prodotto scalare, l’unico movimento è stata una proiezione (un fendente) che ha prodotto un numero e niente più. In altre parole: abbiamo calcolato la componente di un vettore lungo la direzione dell’altro vettore e poi ci siamo limitati a moltiplicare due lunghezze che giacevano sulla stessa retta. Il verso dei vettori è solo servito a vedere se il prodotto era positivo o negativo.

Due vettori per ottenere solo uno scalare… sembra quasi uno spreco. No, no, stiamo attenti a giudicare troppo velocemente le grandezze fisiche, dato che il lavoro, e di conseguenza anche l’energia di cui il lavoro è una differenza, nascono proprio in questo modo. Tuttavia, coloro che amano i colpi di scherma più articolati e dinamici, troveranno pane per i loro denti nel prodotto vettoriale. Ricordiamo ancora che i prodotti tra vettori sono di due tipi: il prodotto scalare (che già abbiamo conosciuto) e il prodotto vettoriale.

Attacco e difesa

Bene, posso subito dire che il risultato di un prodotto vettoriale è ancora un vettore, completamente diverso da quelli di partenza. Essendo un vettore, dobbiamo riuscire a definire molto bene il suo modulo, la sua direzione e il suo verso.  Per rimanere ancora un attimo nel campo della scherma, il prodotto vettoriale vede le due spade agire insieme, ognuna con la sua prerogativa. Una cerca di colpire, ma l’altra devia la lama avversaria e il risultato è una lama puntata lontano dal bersaglio: attacco e difesa insomma, una specie di … presa di ferro.

Concludiamo qua l'ormai troppo “forzato” paragone con la nobile arte della scherma e dedichiamoci a una descrizione più matematica e geometrica. Userò, però, una trattazione che credo sia ben poco seguita sui libri, ma che pone già le basi per il personaggio principale delle nostre “lezioni”: il momento angolare. Normalmente, il prodotto vettoriale si definisce attraverso un paio di regole che vanno più o meno digerite per quello che sono, comportando un certo sforzo mnemonico. Una metodo che a me piace poco… e, quindi, a scapito di una serie più lunga di passaggi, vorrei mettere in luce la dinamicità dell’intera azione.

Andiamo, quindi, per gradi, cominciando dal modulo del vettore prodotto vettoriale. Questo modulo ha anche un significato geometrico non certo trascurabile, che è spesso usato in geometria superiore.

Un modulo … perpendicolare

Per calcolare il modulo possiamo tranquillamente rimanere su un piano. L’operazione da svolgere è mostrata in Fig. 14. Come al solito abbiamo i nostri due vettori v e u. Per il momento, non abbiamo nessun vincolo sul loro ordine di entrata. Per calcolare il modulo entrambi possono svolgere la stessa procedura.  Consideriamo, prima, v.

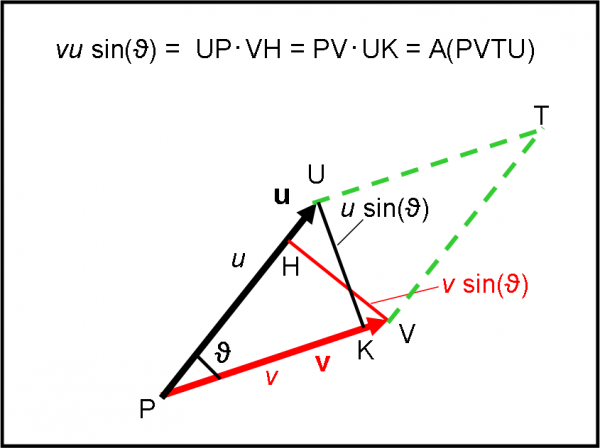
L’operazione non è molto diversa da quella eseguita nel prodotto scalare, ossia bisogna proiettare il vettore v sul vettore u (ossia tracciare su u  la perpendicolare dalla punta di v) in modo da ottenere il solito triangolo rettangolo PHV. La volta scorsa ci eravamo interessati del segmento PH (ricordate?). Questa volta, invece, siamo interessati a VH. Esso è uno scalare, una lunghezza, perpendicolare al vettore u. Le due “spade” formano un angolo retto. Tuttavia, ciò che dobbiamo fare è proprio moltiplicare VH per il modulo di  u (u= PU).

Non sto a perdere tempo a  scrivere la moltiplicazione in questo modo, ma aggiungo subito (e lo dovreste sapere bene) che VH non è altro che il modulo di v moltiplicato per il seno dell’angolo compreso tra i due vettori (considerato sempre positivo e compreso tra 0 e 180°), ossia:

VH = v sin (ϑ)

Possiamo concludere che il modulo del vettore “prodotto vettoriale” è dato da:

modulo  prodotto vettoriale = vu sin (ϑ).

Come avevo già anticipato, possiamo tranquillamente invertire i compiti dei due vettori. Possiamo, infatti, tracciare la perpendicolare dalla punta del vettore u sulla direzione del vettore v, ottenendo così il segmento UK = u sin (ϑ) e poi moltiplicarlo per il modulo v di v. Otteniamo lo stesso risultato di prima, ossia:

uv sin (ϑ).

Abbiamo dimostrato che possiamo sia usare la proiezione di u su v che quella di v su u, ma il modulo del nostro vettore finale non cambia. In termini pratici, possiamo concludere che il modulo del vettore prodotto vettoriale di due vettori u e v, è dato dal prodotto dei due moduli u e v moltiplicato per il seno dell’angolo compreso. Ricordiamoci che l’angolo deve essere sempre considerato tra 0 e 180° (mai negativo).

A questo punto, introduciamo il simbolo che identifica il prodotto vettoriale (una v rovesciata) e indichiamo il suo modulo come il vettore compreso tra due barrette verticali. Questa scrittura ci dice che stiamo lavorando con un numero scalare sempre positivo, in particolare con il modulo di quel vettore. In formula:

|v Λ u| = |u Λ v| = uv sin (ϑ)

L’uguaglianza iniziale (potere invertire l’ordine dei vettori) l’abbiamo potuta scrivere dato che abbiamo ottenuto lo stesso risultato sia partendo con v che partendo con u. Tuttavia, essa vale SOLO per il modulo e non per il vettore finale: stiamo bene attenti!

Area di un parallelogramma

Prima di procedere, guardiamo un attimo che cosa ci permette di calcolare il modulo del prodotto vettoriale. E’ immediato dedurlo attraverso la Fig. 14. Costruiamo il parallelogramma che ha per lati i due vettori, ossia PUTV (lo conosciamo bene… è quello della famosa regola del parallelogramma). Quanto vale l’area di un parallelogramma? Dovreste saperlo tutti: base per altezza.  Una base del parallelogramma è sicuramente PV e la su altezza relativa è UK. Ma il prodotto PV per UK non è altro che il modulo del nostro prodotto vettoriale. Lo stesso risultato si ottiene, ovviamente, moltiplicando l’altra base (UP) per la sua altezza (VH), che da nuovamente il modulo del prodotto vettoriale. Concludiamo, dicendo che il modulo del prodotto vettoriale di due vettori v e u è uguale all'area del parallelogramma costruito sui due vettori.

Quando va a zero il modulo del prodotto vettoriale? Semplicissimo: o quando è zero uno dei due vettori o quando i due vettori hanno la stessa direzione (l’angolo ϑ va a zero e quindi anche il suo seno). Cosa succede, invece, se i due vettori sono perpendicolari? Si ottiene il valore massimo del prodotto (sin (90) = 1) ossia uv: il parallelogramma diventa un rettangolo.

Vettori che girano

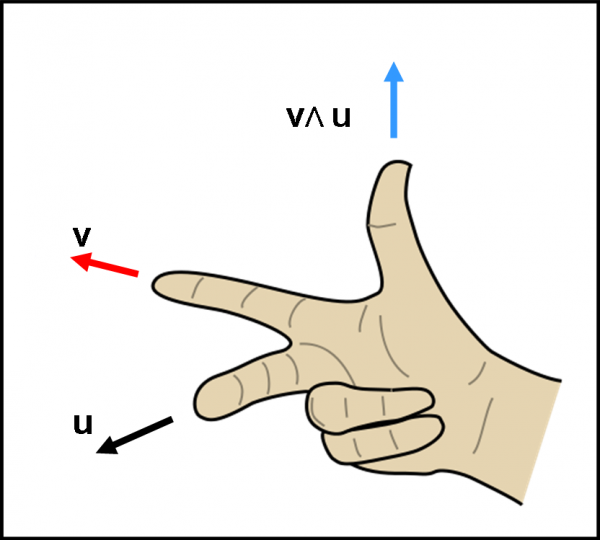
Bene, nel caso del prodotto scalare, a questo punto, avevamo già finito… adesso, invece, abbiamo appena cominciato. Ora c’è da stare molto attenti. Qualcuno si aspetterà la regola della  “mano destra” e invece la introdurrò solo alla fine. Preferisco usare un approccio molto più istruttivo per il prosieguo verso il momento angolare. Consideriamo la Fig. 15a.

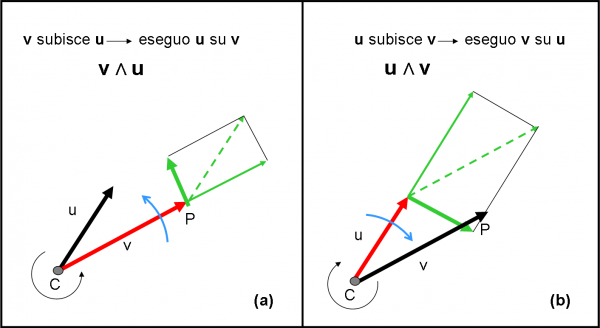
Da ora in poi dobbiamo sempre stare molto attenti a quale vettore compare per primo nel prodotto vettoriale: non stiamo più trattando gli scalari per i quali va sempre tutto bene…

Iniziamo inserendo il vettore v per primo (v Λ u). Cosa dice esattamente il simbolo Λ ? Diciamolo a parole:

Consideriamo il primo vettore come un qualcosa libero di ruotare attorno a una “vite” C. Prendiamo il secondo vettore (u) e trasliamolo fino alla punta di v (linea tratteggiata verde). A questo punto lasciamo che il vettore tratteggiato agisca come sa e come deve sul vettore “rotante” v. Il sosia verde di u non agisce tutto su v.

Per comprendere meglio la sua azione, scomponiamolo secondo due componenti vettoriali (sappiamo farlo benissimo, ricordate la somma dei vettori?): una lungo la direzione di v e una lungo la perpendicolare. Abbiamo i due vettori verdi. Quello diretto lungo CP vorrebbe fare qualcosa, ma non può! Il vettore v può ruotare ma non può allungarsi o restringersi. Insomma, questa componente è del tutto inutile. Ben diversa è la situazione per la componente perpendicolare. Lei  è diretta verso l’alto del foglio e può trascinare il vettore v costringendolo a ruotare nel VERSO della freccia curva verde. E’ esattamente la stessa cosa che abbiamo già visto nel moto circolare uniforme. Il vettore componente perpendicolare di u tende ad andare per la sua strada, ma il vettore rigido v lo costringe a ruotare attorno alla vite C.

Non vogliamo certo fare della cinematica, ma tutto questo discorso ci è servito per capire cosa fa la vite C! Si sta avvitando o svitando? Beh… sta girando in senso antiorario e quindi la vite si svita. In altre parole, la vite si muove verso la direzione perpendicolare al foglio e verso di noi. Bene, questa è la direzione e il verso del vettore prodotto vettoriale.

Attenzione! Tutto ciò lo abbiamo ottenuto in quanto abbiamo considerato per primo il vettore v, ossia quello tenuto fermo dalla vite e in movimento rotatorio a causa del secondo vettore u. Più sinteticamente, abbiamo calcolato direzione e verso del vettore v Λ u. Questa scrittura possiamo perciò esprimerla come: il primo vettore v subisce l’azione “prodotto vettoriale” da parte del secondo vettore u; o -se preferite- il secondo vettore esegue l’operazione “prodotto vettoriale” su v.

Sì, lo ammetto, la mano destra sarebbe stata molto più semplice (e, infatti, la introdurremo tra poco), ma questa definizione un po’ contorta, ci permette già di vedere l’azione rotatoria di un vettore applicato a una certa distanza da un punto fisso. Il primo passo per il momento di una forza e per il nostro amico momento angolare.

Dato che siamo ostinati, continuiamo e spostiamoci nella Fig. 15b. Ormai sappiamo cosa dobbiamo fare. Il prodotto vettoriale è adesso u Λ v. No, non è la stessa cosa! Non siamo più tra i prodotti scalari o tra moduli, ma tra vettori veri e propri. Dobbiamo, quindi seguire l’ordine delle operazioni. Questa volta il vettore che è fissato alla vite diventa u, mentre è v quello che si sposta e si “scompone”. La componente perpendicolare (l’unica attiva) tende ad andare verso il basso del piano del foglio e a causare una rotazione oraria. In poche parole, la vite si avvita, ossia scende nella stessa direzione di prima, ma si allontana da noi.

I prodotti vettoriali ottenuti cambiando l’ordine dei due vettori ci indicano la stessa direzione, ma verso opposto. In poche parole, hanno segno opposto.  Non vale quindi la proprietà commutativa, ma quella anticommutativa, ossia:

u Λ v = - v Λ u.

Per chiarire ancora meglio le idee, disegniamo la Fig. 16, in tre dimensioni, dove si vedono molto bene i due casi appena descritti.

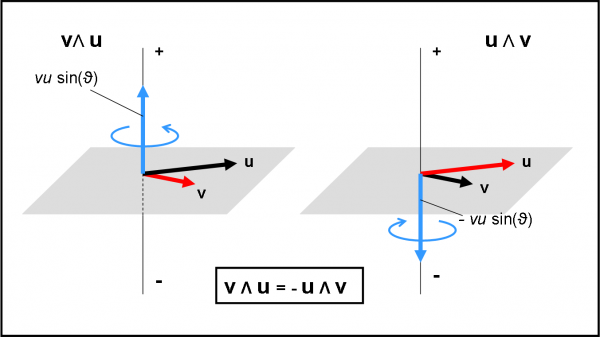
Voglio anche farvi notare un risvolto che ci sarà utilissimo… a tempo debito. Cambiando l’ordine, cambia il segno, ossia il verso, ma non il modulo (quello è sempre uguale). Riguardiamo le Fig. 15a e b. Il vettore v, che subisce a sinistra, è più corto di u, che subisce a destra. Tuttavia, a sinistra, il vettore verde che fa ruotare v (corto) è più lungo di quello che fa girare, a destra, il vettore u (lungo). In poche parole, su un vettore lungo agisce un vettore corto e viceversa. D’altra parte deve essere così dato che il modulo del vettore prodotto vettoriale deve rimanere uguale. Ridendo e scherzando abbiamo già “sfiorato” la conservazione del momento angolare…

Usiamo le dita della mano destra

A questo punto abbiamo capito molte cose e abbiamo anche messo il piede nel terreno della dinamica rotatoria, di cui il momento angolare è uno dei padroni indiscussi.  Possiamo permetterci di introdurre la celeberrima regola della mano destra. Come si può fare per sapere immediatamente qual è la direzione e il verso di un prodotto vettoriale? Il dito indice della mano destra deve essere allineato con il primo vettore, il medio con il secondo vettore. Il pollice ci indica direzione e verso del vettore finale (nella Fig. 17, verso l’alto). Noterete facilmente che se invertiamo l’ordine dei due vettori il pollice imita quello degli imperatori romani negli spettacoli dei gladiatori: pollice verso, ossia verso il basso!

Ricapitoliamo il tutto, definendo compiutamente il vettore definito dal prodotto vettoriale:

Esso è, innanzitutto, un vettore che ha per modulo il prodotto dei moduli moltiplicati per il seno dell’angolo compreso (o -se preferite- ha come modulo l’area del parallelogramma che ha per lati i due vettori). La direzione è sempre perpendicolare al piano individuato dai due vettori. Il verso segue quello del pollice della mano destra.

Nella Fig. 16 i due vettori blu sono proprio i vettori risultanti, invertendo l’ordine dei due vettori nel prodotto vettoriale. La lunghezza dei vettori blu è, ovviamente, il modulo del prodotto vettoriale (uguale per entrambi).

Avanti i più curiosi …

Beh… è stato abbastanza faticoso. Chi vuole può fermarsi qui. Gli altri potrebbero però proseguire e mettere in azione i carissimi e simpaticissimi versori degli assi cartesiani x, y, z. E sì, ora devono comparire tutti e tre, per come è stato definito il prodotto vettoriale.

Noi conosciamo già i versori i e j, relativi agli assi x e y. Chiamiamo k quello relativo all’asse z, come si nota nella Fig. 18.

Prima di procedere, vi propongo un divertente esercizio. Per verificare se avete digerito bene il prodotto vettoriale. Risolvete i seguenti prodotti vettoriali (eseguiti tra versori):

iΛ j =

jΛ k =

kΛ i =

j Λ i =

kΛ j =

iΛ k =

La soluzione la trovate nella Fig. 19 che segue (ma prima pensateci un po’…)

Dopo aver risolto l’esercizio, possiamo determinare le componenti lungo gli assi cartesiani (i moduli dei versori corrispondenti) del vettore prodotto di due vettori, in modo analogo a quanto fatto nell’articolo precedente. Consideriamo il caso più semplice, in cui i due vettori giacciono nel piano x,y.

v = v_x i + v_y j

u = u_x i + u_y j

e, quindi:

v Λ u = (v_x i + v_y j) Λ (u_x i + u_y j) = v_x i Λ u_x i + v_y jΛ u_x i + v_x i Λ u_y j + v_y jΛ u_y j

Ricordando che:

i Λ i = j Λ j = 0

si ha:

v Λ u =  v_y jΛ u_x i + v_x i Λ u_y j

ma vale anche:

j Λ i =- k

i Λ j = k

per cui:

v Λ u =v_x u_y k -v_y u_x k = (v_x u_y - v_y u_x)k      .... (13)

Come volevasi dimostrare: è un vettore che ha per modulo (v_x u_y - v_y u_x) e per direzione e verso quello del versore k, ossia dell’asse z.

Solo per gli … infaticabili

Complicandoci ancora un po’ la vita, si può considerare come piano dei due vettori v e u un piano qualsiasi e non proprio quello x,y. Ciò vuol dire che i due vettori hanno tre coordinate, una per ogni asse cartesiano (z compreso). Segue che:

v = v_x i + v_y j + v_z k

u = u_x i + u_y j+ u_z k   

e con un po’ di lunghi, ma banali, passaggi matematici si ha, alla fine:

v Λ u =(v_y u_z - v_z u_y)i + (v_z u_x – v_x u_z)j + (v_x u_y - v_y u_x)k     .... (14)

La soluzione di questa espressione completa del prodotto vettoriale si può compattare molto bene attraverso il determinante di un matrice quadrata tre per tre. In generale, le matrici sveltiscono enormemente molti calcoli di geometria analitica. Per gli incontentabili, accennerò anche alle matrici in modo da permettergli di trovare velocemente la relazione (14) e poi anche la (13)...

APPENDICE FACOLTATIVA: le matrici 

Quante volte abbiamo usato delle tabelle per riassumere certi dati, mantenendo un certo ordine? La matematica non è da meno e usa una tabella particolarmente utile per una miriade di  situazioni, non ultima la risoluzione di un sistema di equazioni. Noi non vogliamo entrare nei dettagli di questa enorme e importante branca della geometria analitica e dell’analisi matematica, ma la introduciamo solo per utilizzarla in alcuni casi molto particolari, come quello del calcolo delle componenti di un prodotto vettoriale.

Definiamo matrice una tabella di m ∙ n numeri (o elementi in genere) disposti su m righe e n colonne. La matrice si indica come nella parte alta di Fig. 1. Non è altro che un insieme di elementi a, b, c, … disposti per righe e colonne e delimitati da due parentesi curve. La matrice è una raccolta di dati e non un operazione in sé. Si possono, però, trasformare, moltiplicare, dividere, ecc. In particolare, si può calcolare il loro determinante, solo nel caso che la matrice sia quadrata (m = n), per ovvie ragioni matematiche come vedremo sviluppandolo.

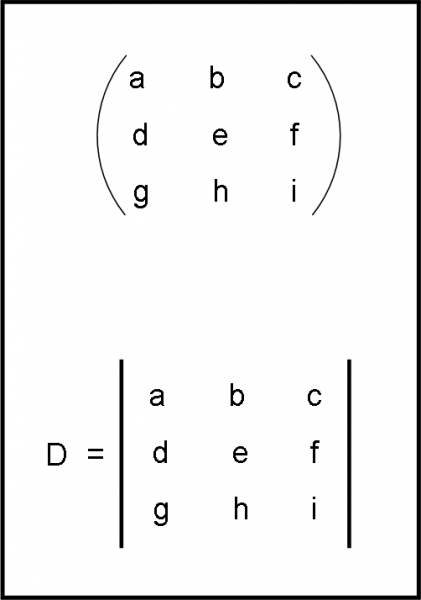
Il determinante è un certo numero o grandezza, in genere, sia scalare che vettoriale, che corrisponde a una certa matrice e che può essere calcolato seguendo certe regole. Esso si indica come la matrice, ma l’insieme degli elementi vengono delimitati da due righe verticali, come si vede nella Fig. 1, in basso. Lo possiamo chiamare Det oppure anche solo D.  Riassumendo: se la matrice è una tabella, il determinante è invece una certa quantità calcolabile.

Il calcolo dei determinanti di certe matrici permette di risolvere velocemente i sistemi di m equazioni in m incognite. Noi ne usiamo uno molto particolare che ci permette di calcolare rapidissimamente il vettore prodotto vettoriale, espresso attraverso le coordinate lungo tre assi cartesiani. In particolare ne useremo uno che ha sia elementi vettoriali che numerici. Anzi… lo lascerò costruire e risolvere proprio ai più preparati di voi…

Limitiamoci ai determinanti con tre righe e tre colonne, quindi con 3 ∙3 = 9 elementi. Da loro seguono, automaticamente, quelli più semplice di 2 ∙2 = 4 elementi.

Cominciamo con quello di tre righe e tre colonne, come rappresentato in Fig. 2. Vediamo come si calcola. Consideriamo la prima riga, ossia quella formata dagli elementi a, b e c (vi dico subito che si potrebbe prendere anche un’altra riga o un’altra colonna, ma limitiamoci a questa soluzione).

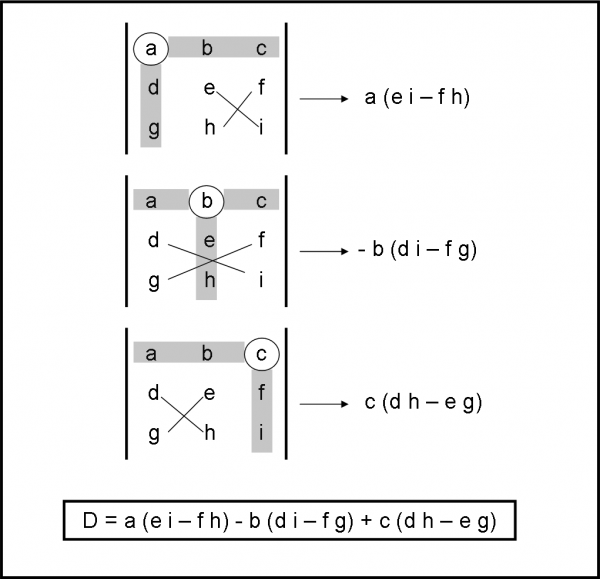
Iniziamo dal primo elemento (a). Cancelliamo, come se non ci fossero, gli elementi che stanno sulla sua riga e sulla sua colonna. Rimangono quattro elementi (e, f, h e i). Moltiplichiamoli a due a due lungo le diagonali e sottraiamo la seconda coppia dalla prima, cioè eseguiamo la seguente operazione:

e i – f h

Questa quantità la moltiplichiamo per a, ossia:

a(e i – f h)

Poi ci spostiamo sul secondo elemento (b) e eliminiamo, di nuovo, la sua colonna e la sua riga. Ci rimangono quattro elementi (d, f, g, i). Moltiplichiamoli, come prima, a due a due seguendo le diagonali e facciamo la differenza tra le due coppie, ossia:

d i – f g

Questa differenza la moltiplichiamo per b e ne cambiamo il segno, ossia:

- b(d i –f g)

Non posso spiegarvi perché dobbiamo cambiare il segno del secondo termine… ma fidatevi che deve essere fatto. Solo e soltanto al secondo termine, mi raccomando…

Passiamo al terzo e ultime elemento (c). Dopo aver cancellato la sua riga e la sua colonna, eseguiamo le solite operazioni su ciò che rimane (d, e, g, h), ottenendo:

d h – e g

e, infine, la solita moltiplicazione per c:

c(d h – e g).

Per calcolare il determinante non ci resta che sommare le tre espressioni (1), (2) e (3), così ottenute, ossia:

D = a(e i – f h) - b(d i –f g) + c(d h – e g)

Sembra una faccenda complicata, ma si impara facilmente. Ci sono molti modi per calcolare i determinanti, ma questo è quello più semplice e rapido nel caso di una matrice (sempre quadrata, ovviamente) con tre righe e tre colonne. Per matrici più grandi (non c’è limite ai termini che si possono mettere in tabella) si passa a metodi più generali e complicati. Tuttavia, alla fisica classica che lavora nello spazio a tre dimensioni, possono -normalmente- bastare tre righe e tre colonne. Lavorando nel piano basta una matrice 2 ∙2.

Applichiamo il metodo appena imparato a un determinante di una matrice di questo tipo, come mostra la Fig. 3. Le cose diventano di una semplicità disarmante…

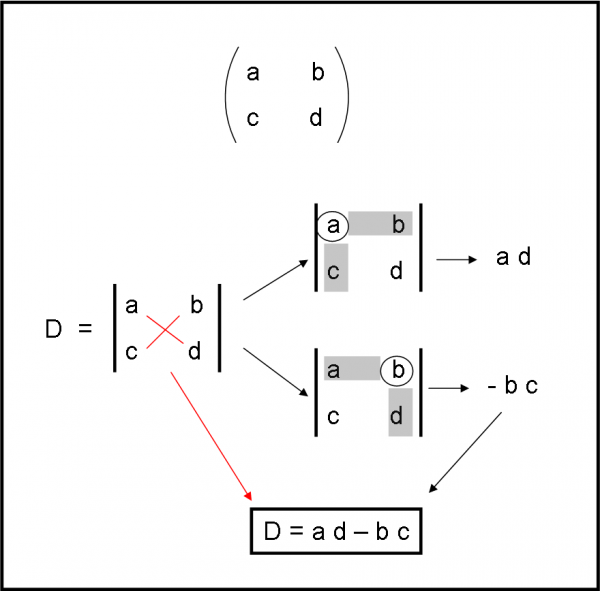
Se prendiamo il primo termine (a) e eliminiamo la sua riga e colonna non ci rimane che un unico elemento: d. Tutto ciò che si può fare e moltiplicare a per d e metterlo da parte:

a d     …. (4)

Passando a b, ci rimane solo c e quindi il tutto si riduce a

- b c   …. (5)     ricordando di cambiare il segno di questo termine, essendo il secondo.

Il determinante sarà uguale alla somma di (4) e (5), ossia:

a d – b c.

Tanta fatica per avere ottenuto esattamente ciò che facevamo per i tre quadratini 2 ∙ 2 del determinante di tre righe e di tre colonne. Insomma, bastava moltiplicare in diagonale e fare la differenza. Beh… abbiamo imparato che il caso 2 ∙2 si risolve immediatamente moltiplicando a due a due in diagonale ed eseguendo la differenza.

Se volessimo fare i raffinati, potremmo indicare qualsiasi determinante  2 ∙ 2 come se fosse un determinante 3 ∙ 3. Basterebbe mettere qualche zero al posto giusto… ma lo vedremo presto.

In realtà, perché sto dando i… numeri in questo modo? Solo per sveltire il calcolo delle componenti del prodotto vettoriale.

In quel caso abbiamo un determinante 3 ∙ 3 molto interessante. Sulla prima riga mettiamo i tre versori i, j e k. In ogni colonna sotto di loro inseriamo le rispettive componenti dei due vettori v e u. Qualcosa come quello di Fig. 4. Sì, in questo caso è un determinante molto particolare, di tipo vettoriale e numerico, proprio come abbiamo accennato all’inizio dell’articolo.

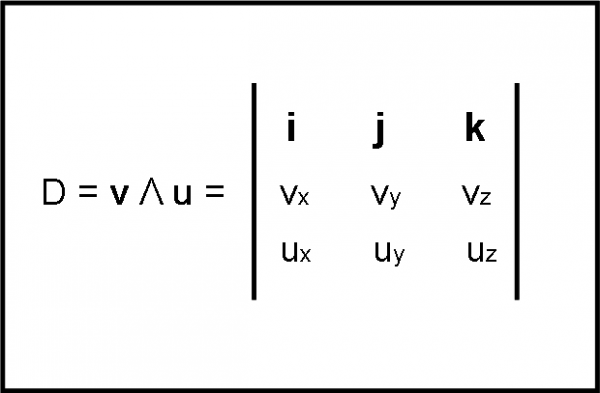
Provate a risolverlo seguendo quanto indicato precedentemente e otterrete la formula (14) .

Come scrivereste il determinante per ottenere la relazione più semplice (13)? Dove mettereste gli zeri? Mi raccomando… non a caso, ma secondo una logica abbastanza banale. Quali sono le loro componenti secondo il versore k (ossia l’asse z) nel caso che i due vettori siano esattamente nel piano x,y? Elementare direi…

Aggiungerò il determinante dopo avervi lasciato un po’ di tempo per provarci… Come conferma dell’esattezza del vostro tentativo avete la relazione (13).

Capito il meccanismo e presa dimestichezza, potrete calcolare tutti i prodotti vettoriali che vorrete, cambiando l’ordine dei vettori o mettendoli in direzioni particolari rispetto agli assi cartesiani o molto altro ancora…

Buon divertimento!

Quantità di moto

Un piccolo riferimento dantesco non fa mai male... Un modo un po' diverso per avvicinarsi a uno dei "pilastri" della meccanica!

Qui vid’i’ gente più ch’altrove troppa,
e d’una parte e d’altra, con grand’urli,
voltando pesi per forza di poppa.
Percoteansi ’ncontro; e poscia pur lì
si rivolgea ciascun, voltando a retro,
gridando: «Perché tieni?» e «Perché burli?».
Così tornavan per lo cerchio tetro
da ogne mano a l’opposito punto,
gridandosi anche loro ontoso metro;

(Vidi più gente qui che in qualunque altro luogo;
divisi in due schiere (avari e spendaccioni), chi in un senso e chi nell’altro,
con grandi urla, facevano rotolare in cerchio dei macigni con la forza del loro petto.
Si scontravano tra loro; e poi, sul luogo stesso dell’urto,
ognuno si voltava, respingendo indietro il peso,
e gridando all’avversario: “Perché tieni?” e “Perché sperperi?”
Tornavano, infine, movendosi attraverso quel cupo cerchio,
da ogni direzione ai punti opposti di partenza,
gridandosi dietro vicendevolmente sempre la stessa infamante cantilena;)

In Fisica vi sono sempre molte strade per giungere a uno stesso risultato. In realtà, esse non differiscono concettualmente tra loro, ma esprimono le operazioni eseguite per ottenere una certa grandezza a partire dalle grandezze di partenza. Cambiando le grandezze di partenza possono cambiare le operazioni da eseguire, ma il risultato deve essere sempre lo stesso, anche se espresso secondo grandezze diverse. E’, quindi, solo un modo diverso di vedere le cose, la cui scelta dipende dal problema che si vuole affrontare e dalle grandezze di partenza. Quando parliamo di momento angolare, ad esempio, si pensa subito ai moti rotazionali. Ed è giustissimo. Tuttavia, per definirlo, potremmo sia partire direttamente dai moti rotazionali  sia da grandezze lineari.

Un esempio l’abbiamo già avuto nella definizione del prodotto vettoriale. Esso agisce su vettori lineari, ma il risultato finale è strettamente legato a un qualcosa che definisce una rotazione. Non per niente, abbiamo introdotto il prodotto vettoriale in modo un po’ diverso dal solito, che già introduce una rotazione (vite che si avvita o che si svita…).

Normalmente, per definire momento angolare, si inizia con parametri legati alla rotazione e quindi si ha una definizione e un’espressione del momento angolare che sembra completamente diverso dalla sua definizione ricavata secondo le leggi del moto lineare. Ma moto lineare e moto rotazionale sono figli della stessa fisica (le leggi della dinamica sono sempre le stesse) e quindi comunque si parta si deve giungere allo stesso risultato. Potremmo, quindi scegliere diversi punti di partenza per arrivare finalmente al nostro attore principale. Noi seguiremo quello che a me sembra più logico e generale e che si rifà alla grandezza fisica che io preferisco in assoluto (ormai lo sapete…): la quantità di moto. Il prodotto vettoriale potrà dare il meglio di sé.

La grandezza “primordiale” dell’Universo

Lasciatemi cercare di spiegare la fisica a modo … mio. Non mi dimenticherò certo dei principi della dinamica (essi devono sempre valere), ma si possono introdurre in modi diversi, come già detto precedentemente.

Sappiamo ormai benissimo che un punto P, libero nello spazio, senza alcun legame con il resto del Cosmo, mantiene il suo moto rettilineo uniforme. Possiamo dire che esso percorre sempre lo stesso spazio in un certo intervallo di tempo. Abbiamo imparato a scrivere questa relazione tra spazio e tempo come velocità del punto.

Qualcuno potrebbe dirmi che il punto potrebbe anche stare fermo. Teoricamente è vero e praticamente non cambierebbe il primo principio della dinamica. In questo caso, infatti, il punto percorrerebbe uno spazio ZERO per qualsiasi intervallo di tempo. La definizione di velocità non cambierebbe, dato che risulterebbe una velocità uguale a zero.

Sono cose che abbiamo trattato in matematica, oltre che in fisica… Basta, infatti, ricordare il coefficiente angolare di una retta e cosa diventa nel caso di una retta parallela all’asse delle x (andate a rileggervi la parte sulla retta e vedrete perfettamente come si esprime il primo principio della dinamica: se m è costante il moto è rettilineo e uniforme e la velocità è costante; se m è uguale a zero, la velocità è nulla e la retta diventa una parallela all’asse x…).

Tuttavia, nell’Universo, niente può essere considerato fermo. Se sembra fermo in un certo sistema di riferimento inerziale non lo è più in un altro. Ci conviene quindi assumere che la velocità sia sempre diversa da zero. L’importante è che sia costante.

Abbiamo introdotto la prima grandezza fondamentale, la velocità v. La scrivo in  grassetto perché essa è un vettore, in quanto per essere individuata ha bisogno di un modulo (la sua grandezza scalare), una direzione e un verso. Per non far sembrare inutili le disquisizioni fatte nei capitoli sui vettori (qualcuno avrà detto: “Ma non dovevamo parlare di momento angolare? Perché tante parole sui vettori e sulle loro operazioni?”), possiamo anche dire che a qualsiasi vettore velocità si può associare un versore u, di modulo unitario, al quale viene moltiplicato il modulo v del vettore v. La scrittura:

v = v u

è sempre valida e può venire utile quando sono necessari certi calcoli o cambiamenti di sistemi di riferimento, ricordando che u ha componenti i, j e k lungo i tre assi cartesiani. Noi -forse- non ne avremo bisogno, ma è bene tenere sempre a mente che niente di quanto descritto precedentemente è veramente inutile. Il concetto di versore e di componenti di un vettore sono concetti fondamentali da digerire molto bene anche se sembrano un cibo senza … calorie!

Torniamo al nostro vettore v. Potremmo dire che è la grandezza fisica più importante di tutte. Essa esiste per qualsiasi punto dello spazio ed è l’unica che ha questa caratteristica veramente globale. Un matematico potrebbe anche accontentarsi, dato che lui sa benissimo come definire un punto, per piccolo che sia. Un fisico, invece, non se ne fa niente della velocità se essa non viene applicata a qualcosa di concreto e di reale. Che sia pur piccolo deve avere consistenza materiale. Vi prego di non pensare al fotone che ha una sua velocità ma non è qualcosa di materiale. Siamo in fisica classica e la MQ non ci può interessare, per adesso (e non confondiamo nemmeno velocità di un punto nello spazio, con “velocità” dello spazio stesso… ).

Il fisico, allora, deve sostituire alla parola “punto”, la parola “corpo”. Per far ciò deve introdurre un’altra grandezza fisica fondamentale che definisca il corpo a cui è associata la velocità.

Non parlo di caratteristica geometrica, come la posizione nello spazio del corpo P, dato che essa è sempre modificabile cambiando sistema di riferimento e può sempre coincidere con l’origine a  un certo tempo t. Ne segue che anche il tempo è di per sé un qualcosa che possiamo far cominciare dove e quando vogliamo. La stessa definizione di velocità ci tranquillizza in questo senso: lei non ha bisogno di un punto di partenza, dato che è una differenza di spazio divisa per una differenza di tempo. Pensateci bene…  le differenze eliminano il problema di un’origine.

Anzi, ormai sappiamo benissimo che la velocità non è altro che la derivata dello spazio fatta rispetto al tempo (v = ds/dt, un rapporto tra un vettore e uno scalare che rimane un vettore). Nel caso di una velocità uniforme, però, la derivata ha poca importanza, dato che rimane costante e non abbiamo bisogno di intervalli piccolissimi e di passaggi al limite. In altre parole, il primo principio della dinamica non ha bisogno di derivate!

La grandezza da aggiungere alla velocità non è altro che la massa del corpo.

Cos’è “questa” massa (ben diversa, concettualmente, da quella che nascerà introducendo la forza gravitazionale) che caratterizza così bene un corpo fisico? Potremmo definirla come la resistenza che il corpo oppone al movimento, qualsiasi sia il sistema di riferimento che si stia usando. E’ un gesto di pigrizia. Con una parola più tecnica la possiamo accostare all’inerzia. Un’inerzia rispetto al movimento che viene imposto dalla velocità.

Consideriamo due corpi che abbiano la stessa velocità. Se il primo deve trascinarsi dietro una massa M molto più grande di m, deve fare una “fatica” ben diversa. Immaginiamo l’Universo come un insieme di corpi di massa diversa, ognuno con un certa velocità. Sembra proprio di essere nell’Inferno dantesco, al capitolo VII, quello degli avari e dei prodighi. Chi è il peccatore che spinge un masso più o meno grande a seconda del peccato? Deve avere un nome, una chiara identificazione fisica. La velocità indica solo il movimento. La massa indica solo quanto sia più o meno pesante la pietra. Ciò che veramente descrive l’azione finale è l’unione di queste due grandezze, ossia la fatica fatta del peccatore. Definiamo così la prima grandezza veramente “attiva” nel Cosmo, quella che tiene conto sia della velocità che della massa da trasportare.

Se la massa fosse unitaria questa grandezza avrebbe un certo valore. Se la massa fosse il doppio, il peccatore dovrebbe mantenere la stessa velocità con un  peso doppio. Ma, analogamente, potrebbe avere la stessa massa ma correre con velocità doppia. E’ facile descrive questa “fatica” come il prodotto tra la massa e la velocità. Più la massa cresce e più la fatica aumenta e lo stesso avviene, a parità di massa, se la velocità aumenta. Se vogliamo che la fatica resti sempre uguale, al crescere della massa dobbiamo diminuire la velocità e viceversa. Ossia, massa e velocità sono inversamente proporzionali.

Bene, basta (per il momento) con i peccatori e torniamo alla dinamica di Newton. Definiamo questa “fatica” come quantità di moto e la scriviamo come moltiplicazione tra la grandezza scalare m e la grandezza vettoriale v.

q = mv

dato che vi è un moltiplicazione tra uno scalare e un vettore il risultato deve ancora essere un vettore (lo abbiamo imparato nelle lezioni precedenti), in cui modulo è proprio dato dal prodotto tra lo scalare m e il modulo v, ossia q = mv.

Se l’Universo fosse stato diverso e non fossero esistite interazioni tra corpi, questa grandezza vettoriale sarebbe stata l’unica, più che sufficiente a descrivere ogni "cosa" del Cosmo. Ogni ipotetica particella di questo strano Universo si sarebbe mossa di moto rettilineo uniforme e non avrebbe mai interagito con nessun’altra particella. La quantità di moto di ogni abitante del Cosmo sarebbe sempre rimasta la stessa. Si sarebbe conservata. La massa è quella che è e lo stesso varrebbe anche per la velocità. Un Universo dominato solo dal primo principio della dinamica.

In realtà, se niente viene a disturbare questa situazione “peccaminosa”,  ciò capita anche nel nostro Universo. Tuttavia, la pace è di breve durata e anche la quantità di moto è costretta a cambiare, anche se fa di tutto per rimanere sempre uguale a sé stessa. Parliamoci chiaro: la massa non può cambiare e quindi non crea problemi. Le velocità vorrebbe seguire il primo principio della dinamica, ma ecco che arriva il secondo a rompere le uova nel paniere.

Purtroppo, l’Universo è molto affollato ed esistono quattro interazioni fondamentali. Due di loro  agiscono solo per corpi estremamente vicini. Un’altra agisce solo se i corpi assumono una carica elettrica. L'ultima, la più debole, rimane comunque e si fa sentire senza aver paura della distanza. Eh sì, non fosse altro che per la gravità, la nostra quantità di moto avrebbe poche speranze di mantenersi costante. Fortunatamente, i suoi effetti possono essere trascurati per distanza molto grandi e, in prima approssimazione, la fisica può anche divertirsi a mantenere costante la quantità di moto (in certe condizioni). Possiamo, perciò, analizzare la nostra “fatica” da peccatori, come una grandezza costante e che cerca di rimanere tale.

I peccatori sono tanti

Nel settimo canto dell’Inferno, però, i peccatori si scontrano spesso e volentieri, subendo azioni esterne. Lo stesso capita nell’Universo, attraverso azioni a distanza o per contatto ravvicinato. Come si comporta, allora, la nostra quantità di moto?

Analizziamola da vicino e introduciamo, attraverso di lei, il secondo principio della dinamica.

Accettiamo che un qualche disturbo esterno faccia variare la quantità di moto, ossia la fatica fatta dall’avaro o dal prodigo. Variare rispetto a cosa? Beh… è ovvio, una variazione rispetto al tempo. Variazione rispetto al tempo? Ma sappiamo bene come trattare questa situazione! L’operazione così descritta non è altro che la derivata della quantità di moto rispetto al  tempo. Ciò vuol dire che possiamo scrivere:

dq/dt = d(mv)/dt

Abbiamo la derivata di un prodotto, dove, però, uno dei due fattori moltiplicativi, la massa m, è uno scalare, ossia un  numero che non cambia, una grandezza costante nel tempo (ricordatevi le operazioni con le derivate). La derivata allora diventa:

dq/dt = m(dv/dt)

Beh… noi siamo ormai esperti di derivate e di moti nello spazio. Sappiamo benissimo cos’è la derivata della velocità. Essa è l’accelerazione e la indichiamo con a (che è anche, per definizione, la derivata seconda della posizione del corpo P, come già descritto nelle ultime lezioni di matematica: d²s/dt² = a)

Abbiamo, allora:

dq/dt = ma

La variazione della quantità di moto non è altro che la massa moltiplicata per l’accelerazione.

Questa variazione è un qualcosa che viene a turbare la tranquillità del nostro peccatore e possiamo chiamarla forza, dato che non è certo cosa semplice cambiare la situazione in cui si trova il condannato. Ci vuole qualcosa di molto “robusto”! Il secondo principio della dinamica ci dice, quindi, che la forza è la variazione della quantità di moto e può essere scritta come massa moltiplicata per accelerazione e indicata con F.

F = ma = m dv/dt = d/dt(mv)

La forza è quindi un disturbo esterno che riesce a modificare la quantità di moto di un corpo che non la cambierebbe per nessun motivo al mondo.

La quantità di moto fa, però, di tutto per conservarsi e ci riesce anche quando la forza che la modifica agisce attraverso una “brutale” interazione con un altro corpo. Non voglio introdurre concetti come impulso e cose del genere, se no descriveremmo piano piano tutta la fisica…

Basta fare un esempio che già conosciamo bene attraverso l’effetto Compton (?!) o -meglio- attraverso il gioco del biliardo. Lo ricordiamo brevemente, da un punto di vista concettuale. In tal modo ci scontriamo anche con il terzo principio della dinamica.

Immaginiamo che il nostro “peccatore” stia subendo una forza costante, ossia che continui a variare la quantità di moto, dato che la forza continua a variare la sua velocità. In questo caso c’è poco da fare… addio alla conservazione della quantità di moto.

Possiamo esprimere in altro modo questa situazione: la quantità di moto di un corpo non cambia se la forza che agisce sul corpo è nulla. Essere nulla, però, non vuol dire che non ci siano forze… vuole solo dire che la risultante di tutte le forze è nulla.

La forza è un vettore e quindi sommando vettorialmente tutte le forze che agiscono sul corpo potremmo ottenere una forza finale uguale a zero (le operazione sui vettori tornano in auge…). Benché in mezzo a un caos terribile la nostra quantità di moto rimane costante. Ci sono mille modi perché ciò avvenga, ma noi ne consideriamo uno semplicissimo (ne abbiamo già parlato, ma è sempre utile ripetere).

Abbiamo il “peccatore” P che si scontra con il “peccatore” Q, proprio come avviene nel settimo Canto… Cosa succede alla loro quantità di moto? Sono entrambi peccatori, devono soffrire la stessa pena e si sentono parte di un unico sistema… Parliamo seriamente.

Il primo corpo sbatte contro il secondo, il che vuole anche dire che il secondo sbatte contro il primo. L’operazione di “sbattere” introduce una forza esterna ai nostri due corpi. Entrano in gioco le interazioni dovute al contatto tra due “pezzi” di materia, ma trascuriamone pure le cause.  Il primo corpo agisce sul secondo imprimendogli una forza F_P. Il secondo, però, non è da meno e risponde con una forza F_Q. Il terzo principio della dinamica ci dice che le due forze devono essere uguali e contrarie.

Cosa succede nel momento in cui avviene l’urto? Il corpo P e il corpo Q diventano un corpo solo. Succede solo per un attimo, ma succede. Le due forze di prima agiscono solo se vi è contatto, ossia agiscono solo in quell’istante. In quell’istante possiamo perciò considerare un corpo unico PQ che ha una certa quantità di moto, data dalla somma delle due quantità di moto dei corpi P e Q. Su questo corpo PQ sta agendo una qualche forza esterna di disturbo? In realtà, sì… anzi due, ma UGUALI E CONTRARIE. In altre parole, la loro somma è uguale a ZERO. Il corpo PQ, a seguito dell’urto, non cambia la propria quantità di moto. Quando i due corpi originari P e Q si staccano e ritornano a viaggiare indipendentemente, la somma delle loro quantità di moto deve essere uguale a quella prima dell’urto. Ognuno ha sicuramente mantenuto la sua massa, ma ha cambiato la velocità, e quindi ognuno ha cambiato la sua quantità di moto, ma si è conservata la somma, proprio quella che avevano nel momento del contatto, in cui formavano un unico sistema,  e in cui le forze createsi si annullavano per il terzo principio della dinamica. In altre parole, i due corpi hanno cambiato la propria quantità di moto, ma si è conservata quella del sistema che li contiene tutti e due. Questa frase è molto importante, perché ci dice che una certa grandezza si conserva a seconda del sistema che si considera.

E’ molto meglio vedere la situazione con qualche formulata facile facile..

Il corpo P ha quantità di moto q_P= m_Pv_P. Il corpo Q ha quantità di moto q_Q = m_Qv_Q. Nel momento dell’urto possiamo scrivere il terzo principio della dinamica:

F_P = - F_Q

Ma il secondo principio della dinamica ci dice chela forza indotta da P è proprio la variazione della quantità di moto di Q

F_P = dq_Q/dt

Vale, però,  anche il viceversa, ossia la forza indotta da Q è la variazione della quantità di moto di P:

F_Q = dq_P/dt

E quindi:

dq_Q/dt = - dq_P/dt

dq_Q/dt + dq_P/dt = 0   (la somma delle derivate è la derivata della somma…)

d(q_Q +q_P)/dt = 0

Se la derivata di “qualcosa” è zero, il “qualcosa” deve essere costante

q_Q + q_P = costante

m_Qv_Q+ m_Pv_P = costante

Se la somma rimane costante lo sarà sia prima che dopo l’urto, dato che al momento dell’urto non cambia la quantità di moto del sistema. Si ha quindi la scrittura più comune:

m_Qv_Q + m_Pv_P = m_Qv_Q’ + m_Pv_P’

dove v e v’ sono le velocità prima e dopo l’urto.

Insomma, questa quantità di moto fa di tutto per mantenersi costante anche se subisce scontri violenti. Il corpo singolo non riesce a farlo ma si allea con chi lo urta, in modo da mantenere costante la somma delle loro quantità di moto! Le conseguenze possono essere molto varie e le vedete nel gioco del biliardo e/o delle bocce. Il peccatore che aveva una certo peso e una certa velocità può andare a sbattere contro un altro peccatore che si era, ad esempio, fermato pur avendo la stessa massa da portare (per qualche urto precedente). Ebbene la conservazione della “fatica” (o della quantità di moto) fa sì che chi prima si muoveva si fermi e chi prima era fermo si metta in movimento. Una specie di legge di compensazione della fatica… Un po’ ciascuno non fa male a nessuno.

Ovviamente, non solo il biliardo sfrutta la conservazione della quantità di moto. Tra le infinite applicazioni basta ricordare quella del fucile (o della pistola o di qualcosa del genere).

Il sistema fucile più proiettile può essere considerato un sistema isolato. Le forze che permettono al proiettile di "uscire" dall'arma da fuoco  sono tutte interne al sistema. Pertanto si può applicare il teorema di conservazione della quantità di moto. All'inizio sia il proiettile che il fucile sono fermi, quindi la quantità di moto totale del sistema è uguale a zero. Di conseguenza deve essere uguale a zero anche la quantità di moto finale . Dopo lo sparo vale allora la relazione  mF · vF = mP · vP (dove la lettera F vale per il fucile e la P per il proiettile). Notate che vF e vP hanno segno opposto, ma la formula è sempre l'ultima che abbiamo scritto precedentemente. Se conosciamo il peso del fucile e del proiettile e misuriamo il rinculo del fucile, è possibile ricavare la velocità del proiettile (oppure il viceversa). Pensateci sopra e troverete molti altri esempi nella vita di tutti i giorni...

Ribadiamo ancora, però, che quello che conta per stabilire una conservazione di grandezze fisiche è il sistema fisico che si considera. Pensate, ad esempio, alla Terra da sola; alla Terra più la Luna; alla Terra più la Luna e più il Sole; all' intero Sistema Solare; ecc., ecc.

Ciò che si conserva in un sistema può benissimo non conservarsi in un altro. La quantità di moto del proiettile passa da zero a un valore molto alto. Lui da solo non conserva un bel niente, ma il sistema proiettile-fucile sì.

La quantità di moto fa parte dei vettori e conosce tutti i loro trucchi

Bene. E’ ora di fare nuove conoscenze nel nostro teatro della fisica. La quantità di moto ci ha insegnato a giocare a bocce e a biliardo. Ci ha anche dimostrato che una ferrea volontà permette di conservarsi costante anche quando sembrano apparire forze “aliene”. Nel far questo ci ha permesso di ricavare e di ripassare i tre principi della dinamica. Niente male per una grandezza fisica così semplice.

Nel frattempo, i vettori si sono divertiti a scambiarsi favori, a sommarsi, a sottrarsi, a moltiplicasi e addirittura a crearne uno nuovo di zecca che occupa una terza dimensione rispetto agli altri due.

Che ne direste di insegnare anche alla nostra quantità di moto i giochi di prestigio dei vettori? Non dimentichiamo, infatti, che anche lei è un vettore! In particolare, è molto interessata al prodotto vettoriale. Non possiamo darle torto: abituata com’è a muoversi sempre in linea retta è ovvio che speri di visitare o -almeno- a dar luogo a qualcosa che la imiti in una diversa dimensione. Non ci resta, quindi, che descrivere come nasce questa “sua” creatura  che andrà a dominare lo spazio a tre dimensioni.

Ormai sappiamo benissimo come si calcola il prodotto vettoriale di due vettori. Basta calcolare il seno dell’angolo tra le loro direzioni e poi moltiplicarlo per i moduli dei due vettori. Sappiamo anche che per fare questa operazione non conta quale sia il primo vettore del prodotto: il modulo rimane sempre lo stesso. Anche la direzione è una e una sola: quella perpendicolare al piano individuato dai due vettori. L’ordine dei vettori è importante solo per determinare il verso del vettore finale. Per far ciò, possiamo usare la mano destra oppure rifarci all’avvitamento o allo svitamento di una vite molto speciale.

Prima di scomodare la quantità di moto, traffichiamo un po’ solo con la sua parte vettoriale, ossia con la velocità. In realtà, quello che andiamo a descrivere vale per qualsiasi vettore, ma è meglio applicarlo direttamente alla velocità. In tal modo abbiamo già fatto il primo passo.

E’ il momento del … momento

Disegniamo, allora, la Fig. 20.   Tracciamo la direzione di una certa velocità costante, ossia quello che capita in un moto rettilineo uniforme. La velocità è abbastanza stufa di agire da sola, senza nessuno spettatore che ammiri la sua banale, continua, ma fondamentale azione. E’ quindi contentissima quando un punto O, immobile, compare dal nulla e osserva il suo percorso.

Si scambiano informazioni nel loro linguaggio (che è poi sempre quello della matematica e della geometria) e si rendono conto di una caratteristica geometrica che rimane costante nella situazione che stanno vivendo.

Qualsiasi sia  il punto di applicazione P della velocità, il segmento variabile OP moltiplicato per il seno dell’angolo tra la direzione OP e la direzione della velocità rimane sempre uguale! Beh… niente di straordinario, era facile aspettarselo dato che, in fondo, è la distanza tra la retta della velocità e la parallela ad essa che passa per O. Possiamo vedere graficamente questa banale considerazione aggiungendo nella figura un punto P’. Risulta, senza ombra di dubbio, che OP sinϑ = OP’ sinϑ’. La faccenda è sempre la stessa, qualsiasi sia la posizione raggiunta da v con O sempre fermo a osservarla (all’infinito le cose si complicherebbero un po’, ma a noi interessa ben poco dato che vogliamo introdurre qualcosa di fisicamente concreto): un bel legame tra la velocità e il punto.

OP e v decidono di sfruttare questa conclusione geometrica e decidono di creare una nuova grandezza fisica. La chiamano momento.

In realtà, la velocità, essendo un vettore, conosce bene tutte le operazioni che possono fare i vettori e, quindi, convince facilmente OP a diventare anch’esso un vettore. Non è qualcosa di nuovo, dato che la distanza tra due punti è stata spesso e volentieri considerata un vettore. Oltretutto –state bene attenti!– la variazione della distanza OP al variare di P, in funzione del tempo, è qualcosa di molto ben conosciuta dalla velocità. Non è altro che lei stessa! Se chiamiamo r il vettore OP, si ha proprio che v = dr/dt. In fondo dr è proprio lo spazio percorso dal punto di applicazione della velocità lungo la sua retta. Non dovrei nemmeno perderci del tempo, ma basta fare, in Fig. 21, la differenza dei vettori r(t + dt), ossia OP’, e r(t), ossia OP, per trovare che la loro differenza è proprio il vettore dr.

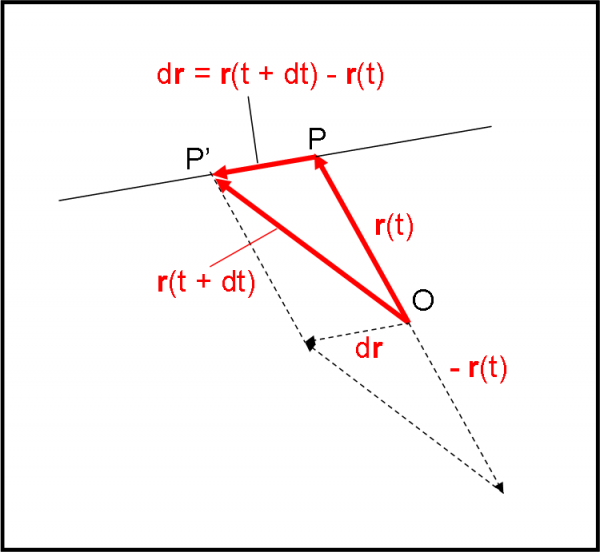
Introduciamo, allora, questa nuova grandezza momento h, che è il prodotto vettoriale tra r e v, ossia h = r Λ v. Scritto in questo modo, indica anche il verso del vettore h. Basta usare la regola della mano destra o quella delle “vite”. Nel caso della Fig. 22, il verso è quello che va verso l’alto.

Tuttavia, prima di pensare al verso, pensiamo al modulo. Esso vale, indipendentemente da quale vettore si mette per primo:

h = r v sinϑ

Un attimo, un attimo… Abbiamo appena dimostrato geometricamente che la grandezza scalare r sinϑ è costante al variare della posizione del punto di applicazione P del vettore v che percorre una linea retta. Ne segue, facilmente, che:

h = costante

Il modulo del momento di un vettore costante, che si muove di moto rettilineo, è una costante. Il modulo è costante, ma è anche costante la direzione e il verso del vettore momento. Possiamo tranquillamente dire che il vettore h è costante. Ovviamente, dobbiamo sempre aggiungere rispetto a quale punto è calcolato e quindi h si chiama momento di un vettore rispetto a un punto fisso O.

Non vi è piaciuto il modo con cui abbiamo dimostrato la costanza di questa grandezza vettoriale? Troppo geometrica? Troppa trigonometria? Bene, otteniamo lo stesso risultato attraverso un po’ di matematica….

Usiamo, nuovamente, la Fig. 20. Il vettore r’ = OP’ non è altro che la somma di due vettori: r = OP e PP’. Possiamo allora scrivere:

r’Λ v = OP’Λ v = (OP + PP’) Λ v = OP Λ v + PP’ Λ v

Ma, attenzione! PP’ e v sono paralleli e, come ormai sappiamo benissimo, il prodotto vettoriale di due vettori paralleli è uguale a zero.  Ne consegue:

r’Λ v = OP Λ v = r Λ v

Esattamente quello che volevamo dimostrare!

Una conclusione veramente ovvia che, però, spesso non viene abbastanza evidenziata nei libri… Eppure questa costanza è proprio fondamentale per far decidere alla quantità di moto di dar vita alla sua nuova creatura. Una grandezza costante non può che dare origine a una’altra grandezza costante. Ormai, il passaggio da momento vettoriale a momento angolare è di un’ovvietà puerile.

Momento angolare o momento della quantità di moto: una creatura perfetta

La velocità si è accorta che il suo momento rispetto a un punto fisso O è una costante. Non resta che proporlo alla quantità di moto che è un vettore, costante come lei. La quantità di moto ne è entusiasta e annuncia la nascita di una sua creatura costante come lei: il momento angolare rispetto a un punto O. Esso non è altro che il prodotto vettoriale tra la distanza rispetto al punto O e il vettore quantità di moto. In parole matematiche, se q = mv, il momento angolare rispetto ad O è definito da:

L = r Λ q = r Λ mv

Con:

L = r mv sinϑ

Cosa ci dice, in pratica, questa nuova grandezza (costante)? Se un certo oggetto di massa m (costante) si muove di moto rettilineo uniforme esso crea, insieme al punto O di riferimento, un vettore costante diretto secondo la regola della mano destra. Questo vettore può essere, ovviamente, applicato in O. Per come è stato costruito potremmo anche chiamarlo (forse più correttamente) momento della quantità di moto. Sicuramente ci fa capire molto meglio con chi abbiamo a che fare.

Come varia questo momento angolare, nello spazio? Innanzitutto, la direzione è sempre perpendicolare al piano dei due vettori e il verso segue la regola della mano destra. Se la retta è più distante dal punto O il momento aumenta il suo modulo, a parità di velocità: interessante, molto interessante; se la velocità aumenta,  aumenta anche il momento angolare (sempre come modulo): la cosa più ovvia, forse; se aumenta il seno dell’angolo ϑ tra i due vettori, aumenta ancora il modulo del momento angolare.

Quest’ultima situazione è particolarmente importante e da studiare più a fondo. Notate, innanzitutto che non ci interessa come vari l’angolo, ma come vari il suo seno. Il seno è una funzione (la conosciamo bene e l’abbiamo studiata a fondo nella relativa lezione di “Matematica”), che raggiunge il valore massimo per un angolo uguale a 90°. Questo ci dice che a parità di distanza OP e di velocità v, si ottiene il massimo valore del modulo del momento angolare se la direzione della velocità è perpendicolare alla direzione OP.

In parole matematiche il valore del modulo del momento angolare, uguale a r mv sinϑ, ha come valore massimo la quantità m v r (sin ϑ = 1).

Questo fatto ci ricorda qualcosa che avevamo eseguito per vedere come girava la “vite” del prodotto vettoriale. Proviamo a scomporre il vettore velocità v, punto per punto, in  due componenti: una radiale (v_R) e una perpendicolare (v_T). Eseguiamo il solito prodotto vettoriale che ci regala il momento del vettore:

r Λ v = r Λ (v_R + v_T) = r Λ v_R + r Λ v_T

Ma, r e v_R sono paralleli e quindi r Λ v_R = 0. Ne segue:

r Λ v = r Λ v_T

Questo “esercizio” vettoriale ci porta a dire che per ottenere il momento di un vettore non è necessario utilizzare tutto il vettore, ma basta considerare solo la sua componente perpendicolare al vettore r.

Qualcuno potrebbe dirmi: “Beh? Perché tanta fatica se conosciamo il vettore v?”. Avrebbe sicuramente ragione… Tuttavia, il ragionamento di prima ci conduce a una conseguenza di importanza enorme. Pensiamo, solo per un attimo, a cosa succederebbe se il vettore v non si muovesse in linea retta, ma descrivesse una curva con il modulo della velocità, v, costante.

Gira e rigira...

D’accordo, la sua quantità di moto cambierebbe da punto a punto come direzione (il moto non sarebbe più rettilineo uniforme), ma manterrebbe lo stesso modulo mv. E se il moto fosse proprio circolare con centro in O? Ossia se r fosse costante? Anche il modulo del momento rimarrebbe costante, dato che r è costante, lo è v, ma soprattutto il seno dell’angolo sarebbe sempre uguale a 1, ossia il modulo finale del momento sarebbe soltanto e sempre v r.

Nel caso della quantità di moto, dato che la massa è costante, sarebbe analogamente costante il suo modulo e anche quello del momento angolare rispetto a O. Tuttavia, c’è un vantaggio in più. Il vettore quantità di moto NON sarebbe costante, dato che cambia di verso e direzione istante per istante, mentre il vettore momento angolare rimarrebbe costante, dato che la sua direzione e il suo verso rimangono inalterati durante il moto.

In parole povere, in un moto circolare uniforme NON si conserva la quantità di moto, ma si conserva il momento angolare. Immaginiamo di vedere questo vettore che punta verso di noi (o in verso opposto se la rotazione avviene al contrario) e che rimane costante mentre la massa m gira attorno ad O. E’ o non è un segnale importantissimo per sapere cosa sta avvenendo al nostro oggetto? E’ o non è una grandezza MOLTO esplicativa? Accidenti, la nostra amica q = mv si è scelta un ottimo “figliolo”: se non può conservarsi lei si conserva il momento angolare!

Ma c’è di più… la quantità di moto non si conserva perché esiste una forza F che agisce continuamente sull’oggetto di massa m e questa forza non è altro che quella centripeta. Tuttavia, sembra che l’esistenza di questa forza non dia nessun fastidio al momento angolare. Lui rimane costante… Come mai? Beh… la risposta è facile: la forza F è sempre parallela al raggio r.

Sono andato volontariamente un po’ avanti, per farvi già sentire il “profumo” dei moti rotazionali e l’importanza del momento angolare. La prossima volta torneremo indietro e descriveremo l’ultima parte con maggiore calma. Tuttavia, il succo e il valore indiscusso del momento angolare si sono già manifestati in pieno.

Complimenti quantità di moto! Hai costruito una creatura meravigliosa…

Anche la forza ha il suo momento

Il prodotto vettoriale ci ha fatto conoscere il momento angolare, una grandezza veramente interessante. Essa deriva direttamente dalla quantità di moto, ma ha il privilegio di rimanere costante anche in “alcuni casi” in cui la quantità di moto può essere costretta a variare. E questi sono casi estremamente interessanti in meccanica… Queste situazioni le vedremo meglio tra poco.

Torniamo al concetto di momento di un vettore. Lo possiamo applicare a qualsiasi vettore e quindi perché non applicarlo a una forza F? In parole povere, tutto il procedimento usato per definire il momento della quantità di moto (ossia il momento angolare) può essere ripetuto per la forza F. Le figure rimangono praticamente le stesse, ma tanto vale riproporle. In  Fig. 23 consideriamo il solito punto O e la forza F applicata in P. chiamiamo come al solito r il vettore che unisce O con P.

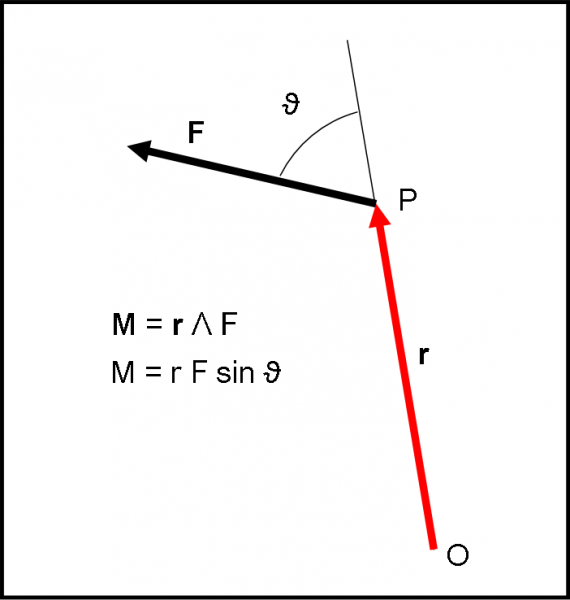
Eseguiamo il prodotto vettoriale tra r e F e otteniamo il vettore  M:

r Λ F = M

il cui modulo è ovviamente:

M = r F sinϑ

Come ormai sappiamo bene, questo vettore è perpendicolare al piano definito dalla forza e dal punto O e il suo verso segue la regola della vite o della mano destra (come preferite). Per analogia con quanto fatto finora chiamiamo questo vettore momento della forza F.

Anche per lui potremmo utilizzare le due componenti (radiale e tangenziale) e notare subito che l’unica componente che determina il risultato finale è quella ortogonale al vettore r. In modo perfettamente analogo a quanto ottenuto per il momento angolare, come mostra la Fig. 24.

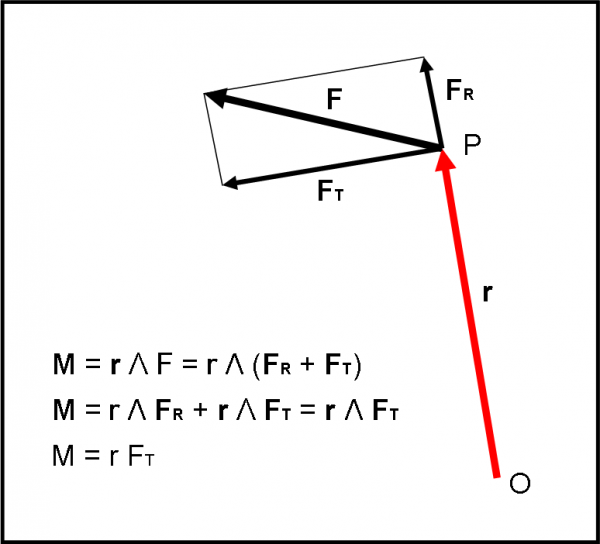
Ricordiamo ancora un punto fondamentale che vale per qualsiasi “momento”. Ha senso parlare di momento (di un vettore qualsiasi, sia esso una quantità di moto o una Forza) solo se indichiamo, sempre, rispetto a quale punto O si riferisce. Senza punto O non esiste r e quindi non esiste alcun momento…

Cosa vuol dire applicare un momento di una forza al punto O. Da un punto di vista “pratico”, il concetto è abbastanza semplice… Immaginate che r sia veramente collegato fisicamente a P. La forza F imprime un’accelerazione a P e lo fa muovere nella direzione del vettore. Varia di conseguenza l’angolo ϑ e si ottiene una rotazione del vettore r. Una rotazione che avviene attorno  a un asse che coincide proprio con il momento della Forza (Fig. 25).

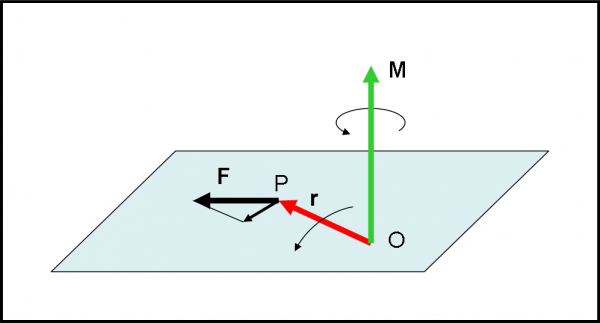
Se poi obblighiamo r a non allungarsi o ad accorciarsi, otteniamo un moto circolare. Qualcosa di simile a quanto avevamo ottenuto per il momento angolare. In quel caso la velocità era a modulo costante e determinava un moto circolare uniforme. Questa volta è costante il modulo della forza, ossia quello dell’accelerazione. Ne risulta un moto circolare ad accelerazione costante e quindi una velocità variabile anche in modulo. In ogni modo, il momento della forza rimane costante.

Prima di scrivere il tutto in modo più sintetico attraverso poche e banali formule, vediamo di fare il punto della situazione legando tra loro il momento di una forza e il corrispondente momento della quantità di moto (momento angolare).

Se applichiamo una forza F a P, di massa m, sappiamo benissimo che facciamo variare la sua quantità di moto, dato che F è proprio la variazione della quantità di moto rispetto al tempo (ricordate?). Se F non è zero, non lo è nemmeno la variazione della quantità di moto. Tutto ciò era stato riassunto dicendo che la quantità di moto si conserva se la risultante delle forze applicate a P è nulla.

Non ci vuole molto a spostare il ragionamento a momento angolare e a momento di una forza. Un momento angolare rimane costante finché è costante la velocità. Se si applica una forza F alla massa m di P, varia il suo momento angolare, dato che varia il vettore velocità. Ne consegue che un punto P mantiene un momento angolare costante solo se è uguale a zero la risultante dei momenti delle forze che gli sono applicate. Attenzione: non ho detto che è nulla la risultante delle forze che gli sono applicate, ma il momento delle forze.

Perché…? Farebbe una qualche differenza? Ebbene sì. E’ vero che se la forza fosse uguale a zero, la quantità di moto si conserverebbe e quindi anche il momento angolare, ma è anche vero che sarebbe una condizione troppo restrittiva! Potrebbe anche essergli applicata una forza tale da far variare la quantità di moto, ma, nel contempo, mantenere costante il momento angolare. E’ possibile? Sicuramente sì! Ne abbiamo già visto un caso perfetto: il moto circolare uniforme.

In questo caso, su punto P agisce una forza, quella centripeta, ma il momento angolare NON cambia. Si capisce subito, quindi, che per far variare oppure no il momento angolare non possiamo limitarci alle forze, ma introdurre i momenti delle forze. Insomma i vettori seguono i vettori, mentre i prodotti vettoriali seguono i prodotti vettoriali (ossia i momenti seguono i momenti).

Concludiamo facilmente. Affinché una forza non sia nulla, ma sia nullo il suo momento, è necessaria una sola cosa: che la forza F sia parallela al vettore r, ossia la componente perpendicolare sia uguale a zero. Beh… la forza centripeta è proprio un classico esempio di tale forza, dato che è diretta sempre e comunque verso il punto O.

Come al solito abbiamo usato tante parole, ma il tutto poteva essere sintetizzato come segue.

Sia L il momento angolare, F la forza e M il suo momento. Possiamo scrivere:

L =  r Λ mv  

dL/dt = d(r Λ mv)/dt = (dr/dt) Λ mv + r Λ d(mv)/dt

Come al solito, però, (dr/dt ) Λ mv = 0 (vettori paralleli), e quindi:

dL/dt =  r Λ d(mv)/dt

Tuttavia, sappiamo molto bene che la derivata rispetto al tempo della quantità di moto non è altro che la forza F, per cui:

dL/dt = r Λ F = M

Una formula fondamentale, anche se ovvia nella sua determinazione. Essa dice che il momento di una forza rispetto a un punto O non è altro che la derivata del momento angolare rispetto allo stesso punto O.

Qualsiasi sia F, l’importante è, quindi, ciò che succede a M. Se M è diverso da zero, il momento angolare è costretto a variare e non può rimanere costante. L’unico modo perché L rimanga costate è porre:

M = 0

Infatti:

dL/dt = 0

e infine

L = costante

Ribadiamo ancora il concetto finale di quanto scritto sia con le parole che con la matematica (ridicola veramente…): il momento angolare di un punto di massa m si conserva se è nullo il momento  delle forze che agiscono su di lui. Potrebbero anche essercene cento, ma se il momento risultante è zero, il momento angolare rimane costante.

Notiamo ancora una volta l’analogia con quanto abbiamo trovato per la quantità di moto: la quantità di moto di un punto di massa m si conserva se è nulla la risultante delle forze che agiscono su di lui. Ovviamente le forze interne si annullano, così come i momenti delle forze interne (i più bravi avranno già capito perché la pattinatrice su ghiaccio deve conservare il momento angolare: la forza che gli fa spostare le braccia è interna al sistema!).

Dinamica del moto rotatorio

Saltando un pochino di qua e di là siamo riusciti ad avere un quadro abbastanza generale dei concetti più importanti della dinamica. Abbiamo avuto a che fare con la massa, l’inerzia di un corpo che vuole soltanto muoversi di moto rettilineo uniforme, con la velocità e sua sorella accelerazione (che cerca sempre di farla cambiare). Abbiamo, soprattutto, conosciuto la quantità di moto, quel prodotto tra un vettore e uno scalare che cerca di conservarsi con le unghie e con i denti.

Abbiamo, però, anche visto che quando la quantità di moto non riesce più a restare costante a causa di una forza che imprime un’accelerazione e , quindi, un cambiamento di velocità, essa si affida a un figliolo ancora più “resistente”: il momento angolare. A lui basta che la forza passi per il centro della rotazione per rimanere costante.

Ciò si riesce a tradurre facilmente dicendo che deve essere nullo il momento della forza che agisce sul corpo. Annullare il momento vuol solo dire, infatti, che la forza deve passare per il centro della rotazione. Una forza perfetta per  lo scopo è proprio la forza centripeta. E’ proprio lei che causa la rotazione del corpo attorno a un punto fisso. In poche parole, il corpo se ne andrebbe tranquillamente lungo una retta, in balia della sua sola quantità di moto che resterebbe invariata, ma viene costantemente deviato da questa forza che tende ad attirarlo verso il centro e lo inserisce in una rotazione che mantiene, però, una velocità costante in modulo. Se non può conservarsi la quantità di moto lo riesce a fare il momento angolare.

Siamo così arrivati a due tipi di movimento abbastanza ben delineati: quello lineare o traslatorio che tende a conservare la quantità di moto e quello rotatorio che tende a conservare il momento angolare. Due moti che hanno molte analogie tra di loro e che adesso andremo a definire sempre meglio

Momento angolare e quantità di moto sono fratelli

Cominciamo proprio con il momento angolare. Esso è stato definito, in modulo, come:

L = mvr   (il seno è diventato uguale a 1, dato che la velocità è perpendicolare al raggio r)

Dove m è la massa, v il modulo della velocità che è costante (ma non lo è la velocità come vettore) e r  è la distanza costante tra il corpo che ruota e il centro della rotazione, come rappresentato semplicemente in Fig. 26.

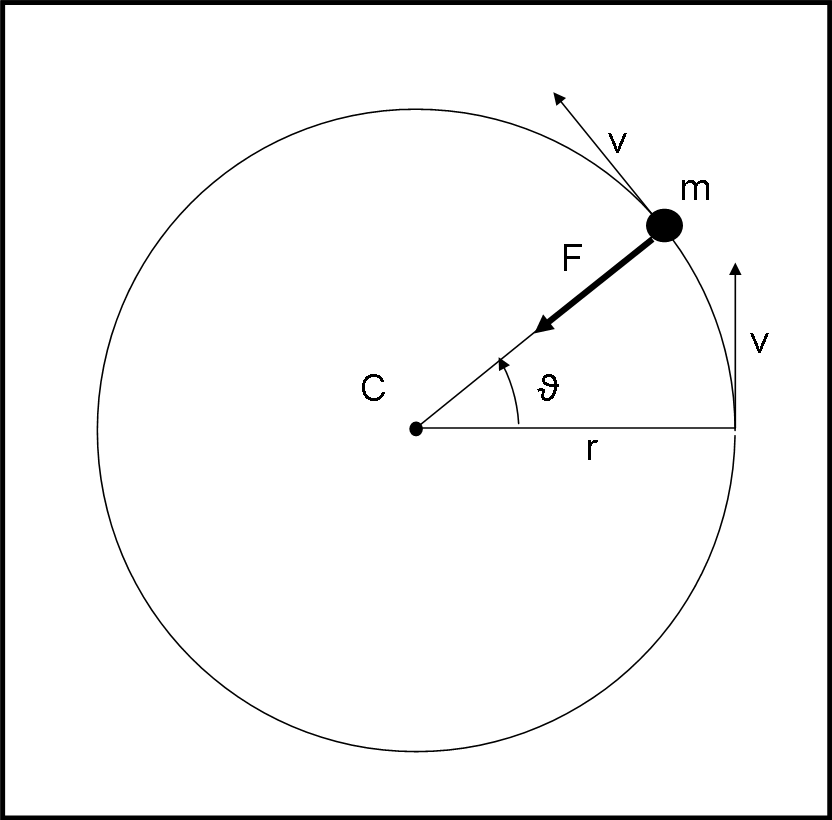
Stiamo parlando di moto rotatorio e quel valore “v” che indica una velocità tangenziale (legata a un qualcosa che continua a cambiare direzione) comincia a dare fastidio. Siamo, però, in grado di sostituirle una nuova velocità che rimane veramente costante, ossia quella angolare, che dice  che l’angolo descritto dal vettore r si muove della stessa quantità nell’unità di tempo. In parole matematiche:

ω = ϑ/t  = 2π/T  (la velocità è costante e la derivata diventa un  semplice rapporto)

Ma, ricordiamo anche che:

v = 2π r/T = ωr

da cui:

ω = v/r

e, quindi:

L = mr²ω

Il posto della velocità lineare v è stato preso dalla velocità angolare ω.

E se il momento angolare, invece che figliolo della quantità di moto, fosse un fratello? Una specie di quantità di moto per i corpi in rotazione attorno a un centro? In fondo, come la quantità di moto si conservava se non intervenivano forze esterne così il momento angolare si conserva se non intervengono momenti di forze esterne. Nel caso di una forza centripeta siamo proprio in questo caso.

L’inerzia a ruotare

Prendiamo il coraggio a due mani e scriviamo:

L = Iω

Qualcosa che ricorda perfettamente:

q = m v

Non ci resta che definire la grandezza mr² come fosse l’equivalente della massa per un corpo in rotazione. In parole semplici, essa rappresenta l’inerzia che un corpo ha quando viene messo in rotazione. Come la massa essa cerca di opporsi a quel girotondo senza fine… Per analogia lo chiamiamo momento d’inerzia. E’ un momento in quanto si riferisce a rotazioni, ma rappresenta pur sempre una … inerzia.

I = mr²

Tutto sembra tornare molto bene: la forza è stata sostituita dal momento della forza, la velocità dalla velocità angolare, la massa dal momento d’inerzia e la quantità di moto dal momento angolare (o momento della quantità di moto).

Non ci vuole molto per scrivere anche la seconda legge della dinamica nel caso dei corpi in rotazione.

Partiamo da:

F = ma

Essa può anche essere scritta come:

F = q/t   (possiamo permetterci di usare il modulo di q che è costante)

Moltiplicando entrambi i membri per r, si ha:

Fr = M = qr/t = L/t = Iω/t = I a_A

Ossia:

M = Ia_A

Dove al posto della forza c’è il suo momento, al posto della massa il momento d’inerzia e al posto dell’accelerazione lineare l’accelerazione angolare (ossia ω/t).

Possiamo anche facilmente dimostrare che l’energia cinetica del moto lineare (E) viene sostituita dall’energia cinetica del moto rotazionale (E_R):

E = ½ mv²

E_R = ½ m (ωr)² = ½ m r²ω² = ½ I ω²

Si possono riassumere  le grandezze lineari e le corrispondenti rotazionali nella Tab. 1

Riflettiamo sulla conservazione del momento angolare

Vale la pena discutere un po’ più a lungo sul momento angolare, l’eroe della nostra avventura. Scriviamolo di nuovo come modulo (sappiamo benissimo cosa sia in realtà: un vettore perpendicolare al piano della rotazione e con il verso che segue la vite o la mano destra).

L = I ω

O, per esteso:

L = m r²ω

Dato che esso si deve conservare, se l’unica forza è quella centripeta, risulta chiaro che se porto la massa m più lontana dal centro (questo spostamento si ottiene con una forza aggiuntiva che passa sempre per il centro e, quindi, ha momento nullo), il raggio r aumenta, ma il momento angolare NON può cambiare. Ne segue che l’unica grandezza che può compensare questo aumento è la velocità angolare. Essa è quindi costretta a diminuire. Se il raggio si accorciasse, succederebbe il contrario: il corpo rivolverebbe più velocemente.

Qualsiasi riferimento al moto planetario NON è casuale! Ricordiamo, infatti, che la forza di gravità é un forza centripeta, così come la tensione di una corda che tiene una pallina a un estremo o del cavo del martello dell’atleta; ma lo è anche l’attrito sulle ruote di una macchina quando curva, la forza di Coulomb tra cariche elettriche di segno opposto, ecc. Ribadisco ancora: “La forza di gravità E’ una forza centripeta, NON UGUAGLIA la forza centripeta! (tanto per mettere bene i puntini sulle “i” … a buon intenditor…)”.

Ma la conservazione del momento angolare ha moltissime altre importanti ripercussioni nel Cosmo. Basta pensare che tutti i corpi che conosciamo ruotano attorno a un qualche punto, spesso il loro centro: le stelle, le galassie, gli ammassi, i pianeti, i sistemi planetari o satellitari, i sistemi doppi, ecc., ecc.. Quello che dobbiamo fare è passare dal moto di un punto attorno a un centro al moto di un corpo o più corpi, più o meno rigidi, attorno ai rispettivi centri. In questo modo scopriremo subito perché la danzatrice sul ghiaccio deve stringere le braccia per ruotare più velocemente e perché una stella di neutroni sembra una trottola impazzita!

La rotazione dei corpi

Il risultato lo otteniamo in modo intuitivamente assai semplice. Basta tenere a mente che il momento angolare di una somma è uguale alla somma dei momenti angolari. Facciamo un esempio molto semplice e pratico in Fig. 27.

Immaginiamo di avere quattro piccole masse che ruotano solidalmente con velocità angolare ω attorno a un punto C. Posso scrivere immediatamente il momento angolare di una sola particella. Per essa vale:

L₁ = m₁r₁² ω

E cosi via per tutte le altre.

Il momento angolare del sistema formato dalle quattro particelle è uguale alla somma dei singoli momenti angolari, ossia:

L = (m₁r₁² + m₂r₂² + m₃r₃² + m₄r₄²) ω

La somma entro parentesi non è altro che il momento d’inerzia complessivo delle quattro particelle.

Immaginiamo adesso di considerare un corpo rigido di forma qualsiasi che ruoti attorno a un centro. Esso può essere scomposto in un numero grandissimo di particelle che si comportano come le quattro precedenti. La somma dei loro momenti d’inerzia diventa il momento d’inerzia dell’intero corpo rispetto al centro C. In realtà, si deve far crescere all’infinito il numero delle particelle infinitesimali e attraverso l’operazione di integrale calcolare abbastanza facilmente il momento d’inerzia complessivo del corpo rigido: se le figure geometriche sono semplici è facile determinarne il volume…

In letteratura si trovano già calcolati i momenti d’inerzia dei solidi più comuni, quali la sfera, il cubo, il cilindro, un’asta rigida, ecc., anche a seconda dell’asse di rotazione che viene scelto. Per l’astrofisica hanno particolare importanza sia la sfera che il disco (uguale a quello di un cilindro di altezza qualsiasi). Soffermiamoci solo sulla sfera, tanto per fare un esempio.

Il momento d’inerzia di una sfera che ruoti attorno al suo centro secondo un certo asse di rotazione è dato da

I = 2/5 M r²

Dove la massa M è la massa della sfera e r il suo raggio.

Diventa ovvio scrivere il momento angolare di una stella o di un pianeta (supposti sferici):

L = 2/5 M r² ω

Se la stessa è costretta a mantenere la sua massa quasi immutata, ma collassa verso un oggetto di raggio estremamente piccolo, è obbligata a mantenere costante il suo momento angolare L. Infatti, la contrazione del raggio è dovuta a una forza che passa per il centro e che quindi ha momento uguale a zero.

Basta fare un po’ di conti e si vede facilmente quanto una stella di raggio solare  deve aumentare la propria rotazione per mantenere costante il suo momento angolare. Non ci stupiamo, quindi, del fatto che le stelle di neutroni abbiano una rotazione rapidissima!

Con ragionamenti analoghi si capisce il raggruppamento delle braccia della ballerina (diminuisce il suo momento d’inerzia) e il trasferimento di momento angolare di un pianeta in momento angolare di pianeta più satellite o di stella più pianeti, ecc., ecc.

Bene, il nostro momento angolare e la sua conservazione ha dato il meglio di sé. D’ora in poi sapremo come trattarlo non appena si farà vivo nelle strabilianti avventure dell’Universo.