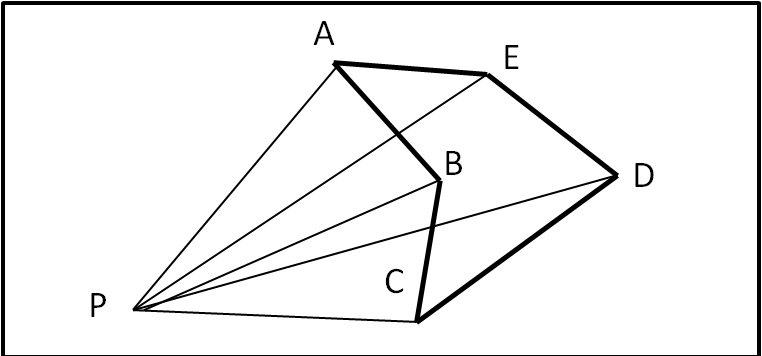
Innanzitutto, un bravo particolare a Leandro che in qualche modo (magari non il più semplice) è riuscito ad allacciare la scarpa... D'altra parte nel poco conosciuto metodo per il calcolo dell'area di un triangolo (e di un poligono qualsiasi) c'è la mano di Gauss. In realtà il metodo "laccio da scarpa" prende anche il nome […]
Descriviamo i due teoremi fondamentali (della divergenza e del rotore) che ci permetteranno di passare dalle equazioni di Maxwell in forma integrale a quelle in forma differenziale.
Il titolo sembra solo una constatazione e nulla più. Spesso viene presa come tale e da essa si innesca il discorso del Pendolo di Foucault e della rotazione della Terra. Tuttavia, esiste una dimostrazione molto pignola che fa uso dei prodotti scalari e vettoriali. Farà un gran piacere agli amanti dei vettori e delle operazioni collegate.
Tiriamo un po’ le somme, dopo i tanti esempi che abbiamo illustrato, per mettere in evidenza la forza di Coriolis e la sua cara sorella centrifuga. Va bene la semplicità grafica, ma un po’ di fisica non guasta mai. In particolare, dobbiamo capire bene quanto e come siano attive, in un vero gioco di squadra! Reputo, perciò, questo semplice articolo molto utile per legare insieme tutto quanto detto finora… non saltatelo!
Beh... Coriolis non ha aspettato tanto (oggi ho deciso di lavorare solo di testa e non di braccia...). Per cui, ecco la nuova versione della prima parte della trattazione della forza di Coriolis, estesa e sicuramente più completa. Fa sicuramente uso di un po' di matematica semplice e recupera nozioni sui versori, vettori, prodotti scalari e vettoriali. Una bella rinfrescata non farà male... Il risultato, però, è estremamente utile per capire al meglio la "nascita" delle forze fittizie in generale. Lo scopo va, quindi, ben oltre la forza di Coriolis.
Nel precedente articolo, che potete rileggere QUI, ho introdotto il concetto di parametri direttori di una retta nel piano. In questo estendiamo il concetto alla retta nello spazio e al piano. Passiamo, quindi, nel riferimento cartesiano dello spazio.
La soluzione è stata già data dai nostri eroi “circolari” (un grazie particolare ad Arturo che ha spronato i silenziosi…). Ne diamo una descrizione semplice e molto dettagliata. Potremo dire di aver fatto nostro un “classico” che ha preso in castagna molti studenti universitari…
Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.
Non abbiate paura, non sono entrato in un discorso sociale o mistico o quello che volete. Stiamo sempre parlando di velocità e di quantità di moto. Quest’ultima, come sapete, è una grandezza fenomenale che mostra tutta la sua perspicacia. Sa che a volte non può conservarsi, ma si costruisce una creatura che riesce a farlo anche in condizioni per lei insormontabili. Entra in scena il nostro attore principale!
In questo articolo ce n’è per tutti i gusti, come si vede dai vari gruppi di asterischi (difficoltà). La parte fondamentale, fino alla … “mano destra”, è abbastanza semplice e deve essere digerita da tutti coloro che vogliono andare avanti. Poi si passa a un piccolo esercizio e allo sviluppo attraverso le componenti (un piacere “estetico” non obbligatorio). Infine, chi non si accontenta ancora, può divertirsi con due vettori posti su un piano qualsiasi. In ogni modo, ho usato una trattazione piuttosto diversa dal solito che permette di spiare all’interno del mondo della dinamica rotatoria, dove il momento angolare ha un posto di primo piano.