La soluzione è stata già data dai nostri eroi “circolari” (un grazie particolare ad Arturo che ha spronato i silenziosi…). Ne diamo una descrizione semplice e molto dettagliata. Potremo dire di aver fatto nostro un “classico” che ha preso in castagna molti studenti universitari…

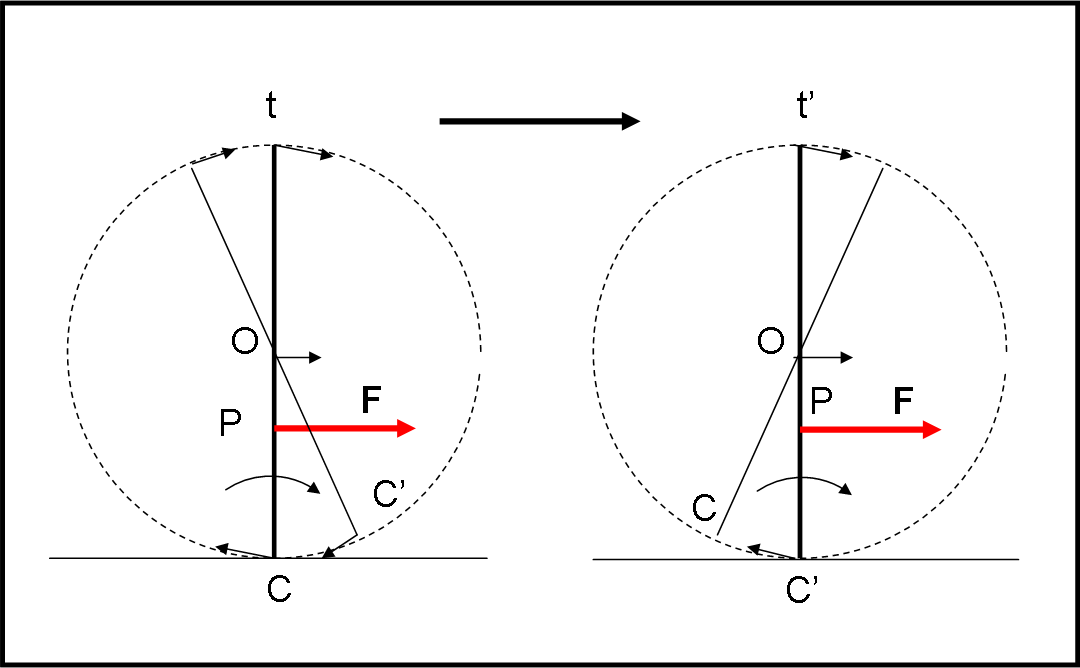
L’unico modo che ha il rocchetto di muoversi (non può strisciare) è quello di rotolare.  L’unico punto attorno a cui effettuare il rotolamento è il punto di contatto con il piano d’appoggio, ossia C. E’, però, una rotazione istantanea, dato che C è costretto a lasciare il piano d’appoggio e venire sostituito con un punto C’, immediatamente successivo, della ruota più larga, o a sinistra o a destra di C, a seconda del verso del moto.

Per capire meglio la situazione, basta sostituire il rocchetto con una serie infinita di aste rigide fissate nel centro O come mostrato in Fig. 1. L’asta rigida corrispondente al punto di contatto C (al tempo t) ruota sotto l’azione della forza F e viene sostituita (al tempo t’ > t) dall’asta che ha come punto di contatto istantaneo C’. In parole ancora più semplici: l’asta rigida istantanea CO “cade” verso destra per effetto della forza F che la fa ruotare in quella direzione. La caduta viene bloccata dall’asta rigida e solidale C’O che ne prende il posto. Come conseguenza l’intero sistema si muove verso destra, effettuando nel contempo una rotazione attorno a O.

Ho cercato sul web una figura che rappresentasse una ruota con tanti piedi (sono sicuro di averla vista varie volte), ma non l’ho trovata… Ne ho fatto, quindi, uno schema che sia abbastanza indicativo in Fig. 2.

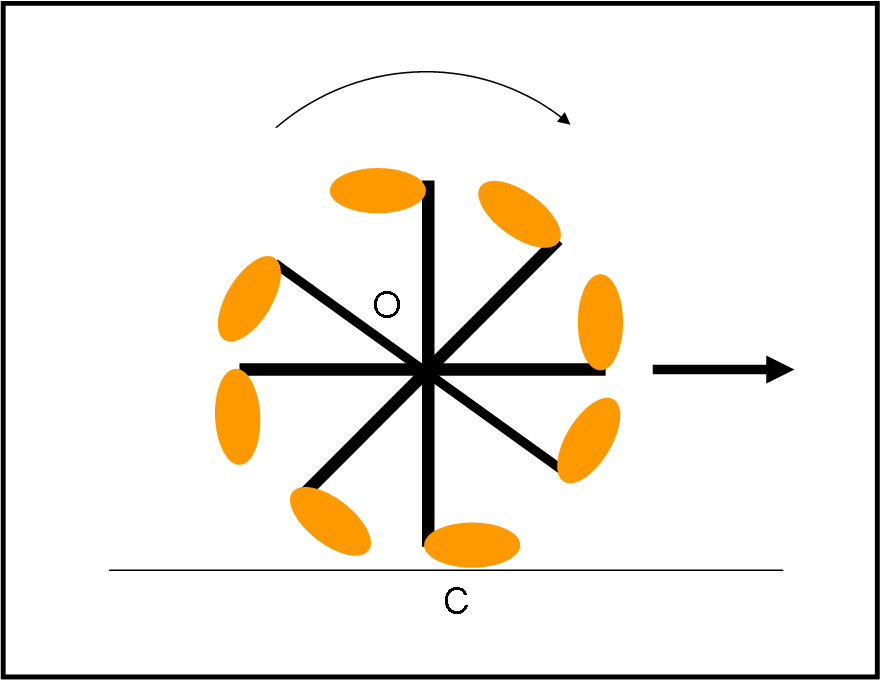
Se agisce una forza diretta verso destra, la ruota si sposta verso quella direzione dato che il centro di rotazione istantanea è C.  La forza è applicata in modo da causare una rotazione istantanea  attorno a C. Tuttavia, dato che la struttura è ancorata in O e perfettamente simmetrica, lo spostamento verso destra si somma a una rotazione attorno a O.

Lasciamo da parte ruote e piedi e torniamo a qualcosa di un po’ più fisico. Ricordando il momento di una forza e il prodotto vettoriale (parte finale di questo approfondimento). Il succo di tutto il discorso è schematizzato in Fig. 3.

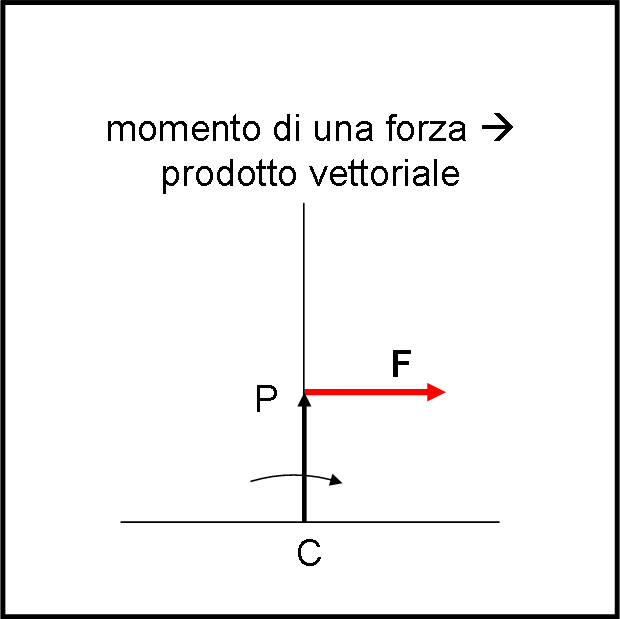
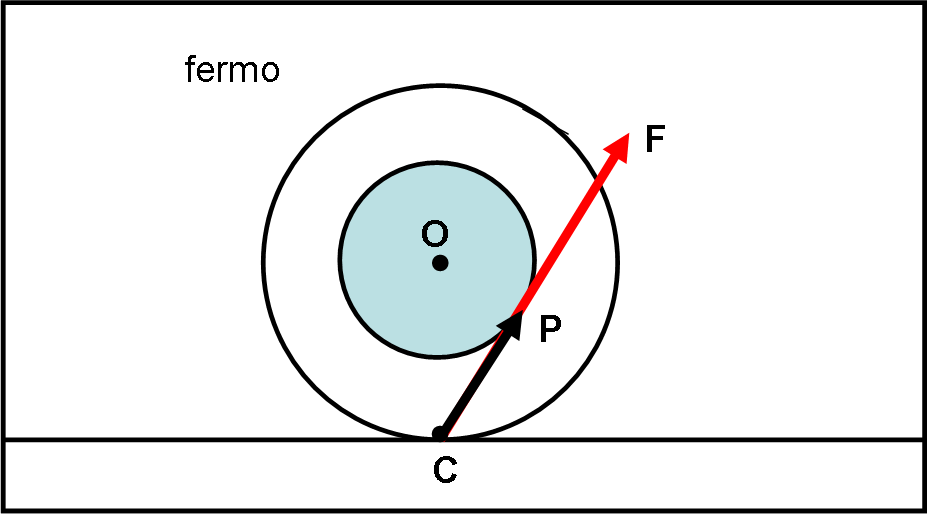
Abbiamo il vettore che identifica il punto di applicazione della forza F (ossia P) rispetto a C. Esso è dato da CP. Abbiamo, poi, la forza F applicata in P. La direzione della forza è proprio perpendicolare al vettore CP e quindi  si ottiene una  rotazione di CP attorno a C (vedi Fig. 25 dell’approfondimento sul momento angolare). Stiamo parlando del momento di una forza che equivale al prodotto vettoriale tra i vettori prima definiti. Il momento è diretto verso di noi o in senso opposto a seconda della direzione di F (regola della mano destra o vite che si svita o s’avvita).

Ne consegue che il rocchetto si muove da una parte o dall’altra solo in base al momento della forza F rispetto al punto di rotazione istantanea C.

La Figura 4 mostra un caso di  movimento verso destra per una direzione della forza non perpendicolare al vettore CP.

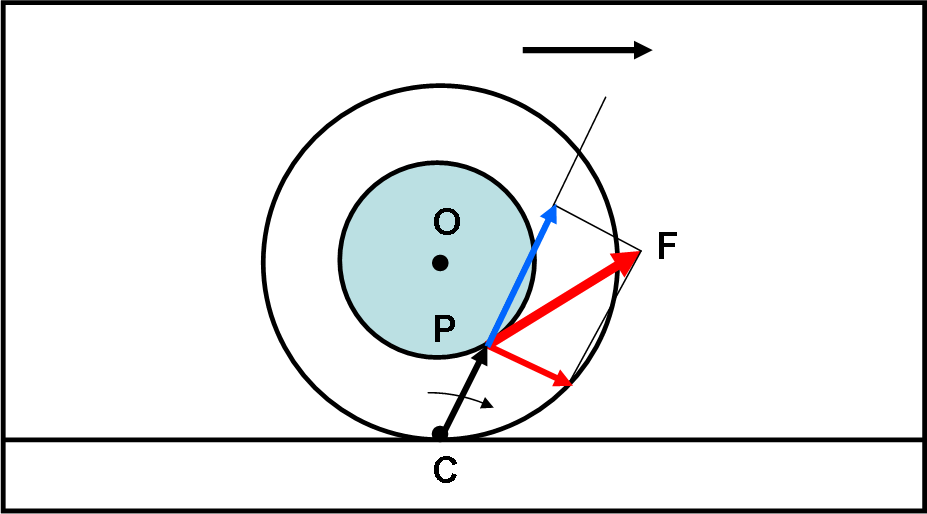
Come imparato nell’approfondimento, si può sempre scomporre il vettore forza F in due componenti molto utili. Una è quella diretta proprio lungo la congiungente CP e l’altra è quella normale a CP. La prima componente non causa rotazione (il prodotto vettoriale è ZERO). Quella che conta è solo la componente normale che è diretta verso destra.

Cosa analoga capita nella Fig. 5, ma questa volta la componente nomale “attiva” è diretta verso sinistra: la rotazione avviene in verso antiorario e lo spostamento del rocchetto è verso sinistra.

La conclusione, senza bisogno di introdurre formule (facilissime), è che il rocchetto si muove nella direzione indicata dal momento della componente normale alla forza. Va verso destra o verso sinistra a seconda dell’angolo formato dalla forza F e dalla congiungente CP. In particolare, la direzione che fa da confine ai due casi è quella che corrisponde alla forza diretta proprio nella direzione CP (Fig. 6). In questo caso il momento della forza (il prodotto vettoriale) è uguale a ZERO e il rocchetto non può rotolare e quindi spostarsi (ricordiamo che non può SCIVOLARE sul piano d’appoggio).

Mi compiaccio per come alcuni hanno affrontato il quiz e per come è stato risolto… Forza, adesso, all’attacco dello specchio parabolico (ci vuole un piccolissimo integrale, niente di più…)!

P.S.: carta igienica e yo yo.

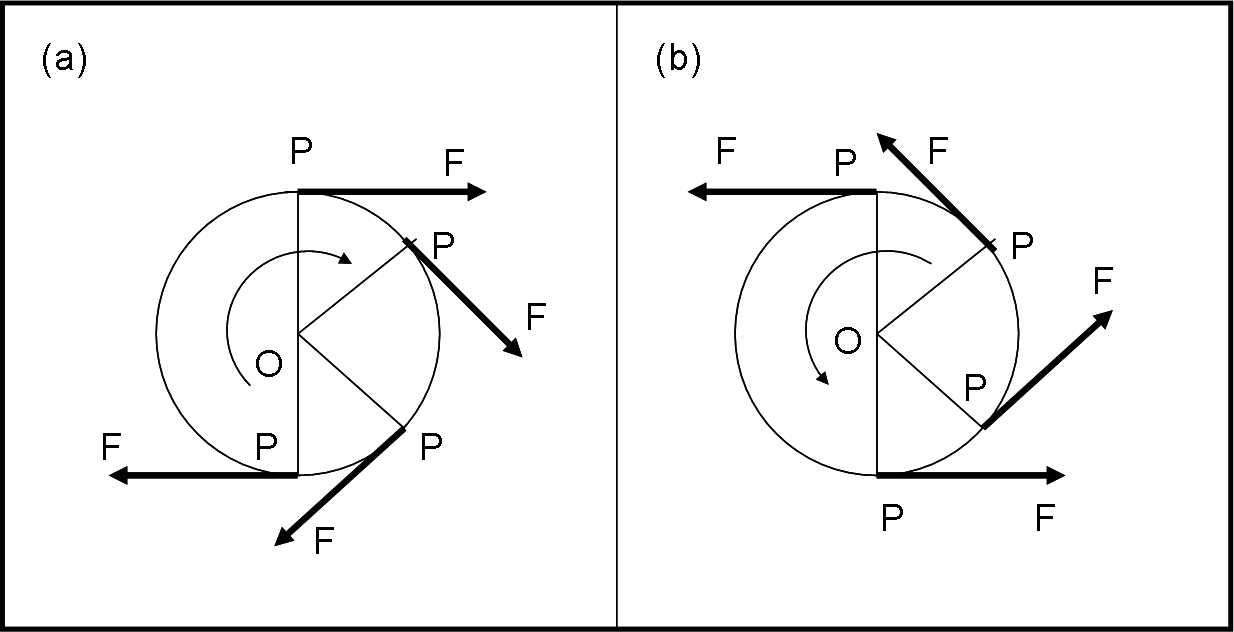
Il caso del rotolo dei carta igienica è decisamente diverso e semplificato. Il rocchetto è fissato nel centro O, per cui è il verso della forza F, e il suo momento rispetto a O, a decidere la rotazione, come si vede bene nelle Fig.re 7a e 7b.

Nello yo yo si ha una ulteriore complicazione, dato che il centro O può spostarsi e le forze che agiscono sono due: quella di gravità e quella impartita dalla mano. Un problemino alquanto intricato e non banale… magari lo tratteremo la... prossima estate.

Il quiz si trova QUI