Categorie: Fisica classica
Tags: direzione movimento quiz rocchetto filo yo-yo
Scritto da: Vincenzo Zappalà
Commenti:14
QUIZ: da che parte si muove il rocchetto? **
Questo quiz è veramente un classico e, quindi, può darsi che molti lo conoscano già… Li prego, perciò, di lasciare parlare gli altri. Esso è in qualche modo “contro intuitivo” e viene proposto come test di entrata in molte università americane. Ricordate i vecchi rocchetti per il filo da cucito? Bene, abbiamo solo bisogno di uno di loro. Vi prego anche di cercare di risolverlo senza passare alla prova pratica (la potete fare dopo…).
Nella Fig. 1 vi è una visione schematica del rocchetto attorno a cui è avvolto del filo. Il raggio della parte con il filo sia R, mentre il raggio delle due ruote esterne sia r > R. Il gioco sta tutto nel tirare il filo con una certa forza F, di modulo costante.
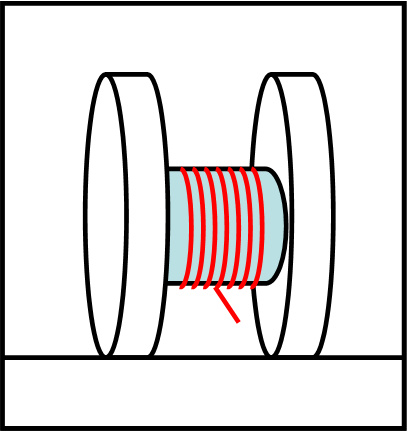
La variabile è quindi l’angolo ϑ che il filo forma con la linea orizzontale, come mostrato in Fig. 2 (il rocchetto è visto di lato). Ricordiamoci che il rocchetto rotola senza scivolare.
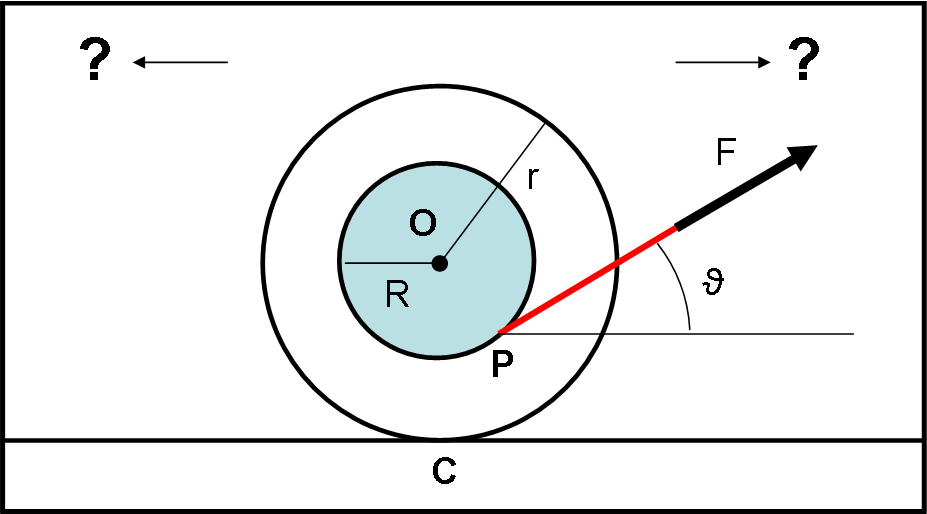
Vi sono vari metodi per risolvere il problema e dimostrare cosa fa il rocchetto. Noi siamo interessati al concetto e non a tanti calcoli, per cui chiedo soltanto da che parte si muove il rocchetto e se la sua direzione cambia a seconda del valore dell’angolo ϑ. La dimostrazione ha bisogno soltanto di un unico concetto grafico e di una giusta definizione del problema (niente formule quindi… ma un paio di figure, al massimo).
Il quiz si ricollega in qualche modo a quello più semplice della “carta igienica” e a quello più complesso dello “yo-yo”.
QUI trovate la soluzione del quiz






14 commenti
Nella figura, tenendo conto del testo del quiz ("Il raggio della parte con il filo sia r, mentre il raggio delle due ruote esterne sia R > r"), credo che le lettere indicanti i raggi , quello della della parte di rocchetto su cui si avvolge il filo e quello delle ruote esterne, debbano essere invertite.
Accattivante e simpatico anche questo quiz
Come ha scritto Vincenzo, "Questo quiz è veramente un classico e, quindi, può darsi che molti lo conoscano già… Li prego, perciò, di lasciare parlare gli altri." Quindi ora mi sto chiedendo, visto che nessuno ancora ha risposto, vuoi vedere che lo sanno tutti ? Ma se è così, qualcuno dovrà pur dire da quale parte va il rocchetto a seconda del valore dell'angolo teta
Dai, su, lettore che non hai ancora risposto, però vorresti farlo, rompiamo il ghiaccio, siamo tra amici.
Giusto, Arturo!
Non dovrebbe essere difficile, forse basta pensarci un "momento"... io l'ho fatto, ma siccome con i quiz ho litigato da piccola (o loro hanno litigato con me?!), tanto per cambiare non sono per niente convinta della soluzione che penso di aver trovato e preferisco non pubblicarla per non confondere le idee
Vi do un suggerimento. Le uniche altre forze in gioco sono quelle di reazione che si applicano al punto C.
wow, tre suggerimenti negli ultimi tre commenti :
Io : "qualcuno dovrà pur dire da quale parte va il rocchetto a seconda del valore dell'angolo teta" --> implicitamente ho suggerito che , si, la direzione del moto del rocchetto dipende dal valore dell'angolo teta
Daniela: ci ha pensato un "momento"...
Leandro: punto C
Sarebbe bello riuscire a spronare qualche nuovo lettore del Circolo a dire la sua, ora che la strada è ...quasi spianata
Immaginiamo il carro dei Carraresi, i buoi davanti, pianto tipico “gioco delle bocce”. Le ruote rotolano, basta vincere l’attrito volvente.
Togliamo le ruote del carro per realizzare il rocchetto, tiro io personalmente la fune, vinco l’attrito volvente che aumenta con la velocità, la fune si avvolge.
Da figura 2 si vede la componente orizzontale che vince l’attrito volvente.
L’aderenza o “attrito statico” impedisce alle ruote di slittare. Io tiro piano piano e la fune si avvolge.
Se invece tiro in verticale freno le "ruotone" che oramai avanzano spedite………..
Rompo il ghiaccio anche se non ho una risposta convincente. Le considerazioni che ho fatto sembrano portare a conclusioni opposte.
Se il rocchetto non slitta sul pavimento ed il filo non slitta srotolandosi ed arrotolandosi, significa che:
- filo si srotola <=> rocchetto a sinistra
- filo si arrotola <=> rocchetto a destra.
Qui la prima considerazione dubbia.
La forza applicata, indipendentemente dall'angolo, sembra causare lo srotolamento del rocchetto. Per quanto detto sopra la conclusione sarebbe: a sinistra indipendentemente dall'angolo. Ma non sembra sia così dagli indizzi che Arturo Lorenzo ha riassunto.
Seconda considerazione, forse più vicina agli indizzi.
Se il rocchetto non slitta, significa che il punto di contatto del rocchetto è istantaneamente fermo rispetto al pavimento. Quindi il rocchetto istantaneamente ruota intorno ad un asse che passa per C (non intorno all'asse centrale del rocchetto). Istantaneamente perchè questo asse cambia continuamente.
Il verso del movimento dovrebbe dipendere dal momento generato dalla forza rispetto a questo asse. Se è orario (-arcocos(r/R)<theta<arcocos(r/R)) il rocchetto dovrebbe arrotolarsi ed andare verso destra. Intuitivamente mi sembra molto strano.
Viceversa se antiorario (arcocos(r/R)<theta<360°-arcocos(r/R)) il rocchetto dovrebbe srotolarsi andando verso sinistra.
esatto
In effetti, il punto C è quello che si definisce "centro di istantanea rotazione". In pratica, la ruota, in questo caso il rocchetto, nel sistema di riferimento solidale al piano di rotolamento, rotolando senza strisciare lungo il piano, istante per istante ruota intorno all'asse rappresentato in sezione proprio dal punto C. Si tratta allora di vedere se la forza F, in base al valore dell'angolo , induce sul rocchetto una coppia (o momento) in senso orario (rotolamento verso destra) o antiorario (rotolamento verso sinistra).
, induce sul rocchetto una coppia (o momento) in senso orario (rotolamento verso destra) o antiorario (rotolamento verso sinistra).
Nella figura seguente, la forza F induce una coppia che tende a far ruotare il rocchetto in senso orario attorno all'asse (perpendicolare al monitor del PC) che in sezione vediamo indicato dal punto C:
Nella seconda figura, invece, la forza F induce una coppia che tende a far ruotare il rocchetto in senso antiorario attorno all'asse suddetto:
E' interessante notare che se la retta di applicazione della forza F passa proprio per il punto C, la coppia si annulla e il rocchetto resta fermo.
Dalle due suddette figure è agevole, con poche considerazioni geometriche, ricavare la formula che esprime la coppia della forza F rispetto all'asse per il punto C, in funzione dell'angolo:
dove il segno + vale nel caso della prima figura (rotazione in senso orario) e il segno - vale nel caso della seconda figura (rotazione in senso antiorario).
Per
la coppia si annulla. Se, ad esempio, è R = 2r, l'angolo in corrispondenza del quale la coppia si annulla è di 60°.
Vi confesso che, dopo essermi risposto sulla carta, ho verificato la risposta con il rocchetto della cordina nautica che uso ogni tanto per lavori in terrazza...
Come è disegnato in figura 2, la forza F genera un momento che fa ruotare in avanti nel punto C di istantanea rotazione?
Trascurando la forza di attrito volvente che frena, comunque sia, il moto.
bene, bene, si sono mossi in tanti...
quasi quasi meritereste lo yoyo...
ci sentiamo al mio ritorno (sono di fretta....)
Io ho provato a scomporre F nelle due componenti perpendicolare e parallela al piano, a questo punto dovrei trovare il momento totale rispetto a O, che a seconda del valore di theta mi dirà da che parte si muove il rocchetto... ma qua mi sono impantanato


ciao Marko, se il calcolo lo fai rispetto a C trovi la stessa soluzione indicata nel mio precedente commento.
un aiutino in più per chi vuole vivere facile... anche senza coppie...
Andate a vedere la Fig. 25 dell'approfondimento suol momento angolare... Basta scegliere il punto O giusto, scomporre la forza lungo la direzione O-punto d'applicazione e la sua normale. La componente lungo la congiungente non agisce. La perpendicolare sì! Basta fare il prodotto vettoriale tra congiungente (vettore) e componente perpendicolare della forza e vedere dove è diretto il vettore risultante. Si svita o s'avvita? regola della mano destra...
Se la componente perpendicolare alla congiungente è zero il prodotto vettoriale è zero e quindi....