Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

 

Beh... Coriolis non ha aspettato tanto (oggi ho deciso di lavorare solo di testa e non di braccia...). Per cui, ecco la nuova versione della prima parte della trattazione della forza di Coriolis, estesa e sicuramente più completa. Fa sicuramente uso di un po' di matematica semplice e recupera nozioni sui versori, vettori, prodotti scalari e vettoriali (che abbiamo ampiamente trattato QUI). Una bella rinfrescata non farà male... Il risultato, però, è estremamente utile per capire al meglio la "nascita" delle forze fittizie in generale. Lo scopo va, quindi, ben oltre la forza di Coriolis.

La cosiddetta forza di Coriolis è una forza fittizia che nasce per spiegare vari fenomeni in un sistema rotante. Il suo interesse è enorme, dato che gli effetti che comporta sono ben visibili sul nostro pianeta. Essi sono anche spiegati abbastanza facilmente in modo qualitativo, anche se spesso si fa una confusione terribile da caso a caso. La nostra intenzione è quella di descriverli in modo chiaro e farne notare le differenze concettuali.

Possiamo solo anticipare che far correre un oggetto su un disco rotante senza attrito comporta condizioni di partenza che risultano fondamentali, me che spesso vengono tralasciate o nascoste. Potete cominciare a pensarci… una cosa, ad esempio, è vedere passare sopra una piattaforma girevole un’astronave aliena che proviene da chissà dove e si dirige chissà dove e un’altra è far partire dal bordo del disco un aereo di linea. Così come sono diverse le condizioni di qualcosa che parte dal centro o dal bordo del disco. Ma, li vedremo e li descriveremo con la massima attenzione e chiarezza (almeno spero), sfruttando le capacità dei nostri grandi collaboratori molto più tecnologici di me, come Paolo, Arturo e spero anche molti altri.

Non solo Coriolis

La determinazione matematica della forza di Coriolis è spesso spiegata in modo quasi “rocambolesco” e la volontà di semplificare porta a risultati poco chiari se non addirittura errati. Una sua trattazione veramente esauriente e corretta abbisogna dell’introduzione dei versori, delle derivate e del prodotto vettoriale. Tutte cose che abbiamo già trattato. La descrizione matematica completa sarebbe quindi alla nostra portata.

Tuttavia, è cosa abbastanza “noiosa” a causa dei molti passaggi. Ho provato a farne a meno, limitando, per quanto possibile, l’utilizzo dei versori, dato che il concetto di fondo risulta abbastanza intuitivo. In questo modo, sicuramente "abbastanza" corretto, capiremo perfettamente come nascono le forze apparenti quando si descrivono posizione, velocità e accelerazione in  due sistemi di riferimento in moto relativo NON INERZIALE. Otterremo, così, qualcosa di molto più generale e fondamentale rispetto alla determinazione della sola forza di Coriolis. Una rinfrescata (QUI), però, non sarebbe male…

Moti relativi

1. Posizione e velocità

Nella Fig.1, disegniamo due sistemi di riferimento cartesiano, con origine in O e O’. Possiamo anche partire con gli assi paralleli tra loro.

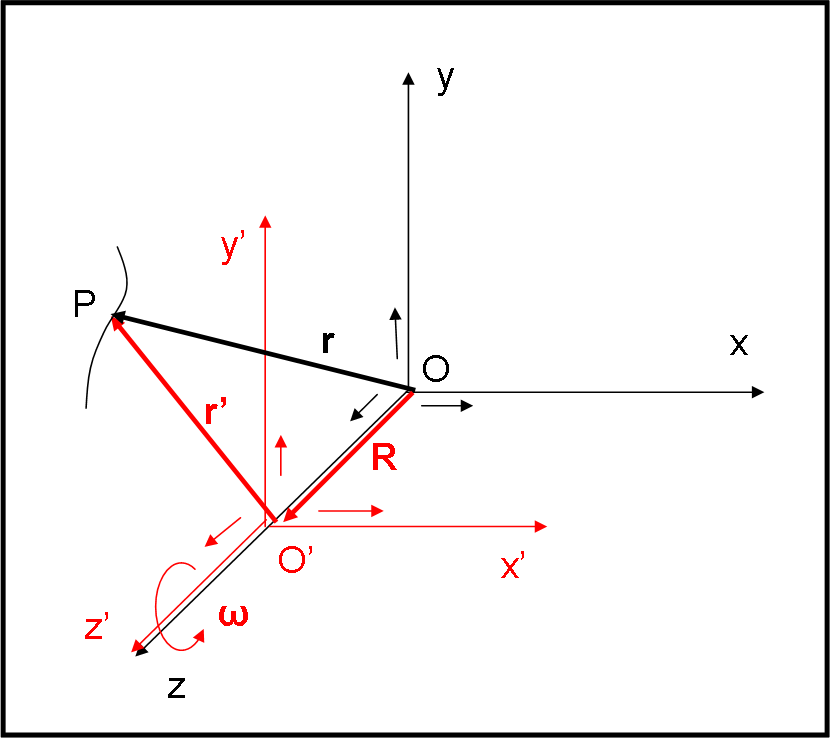
S(Oxyz) è il sistema fisso, mentre S’(O’x’y’z’) è il sistema in movimento. Consideriamo un punto P che descrive la sua traiettoria e indichiamo la sua posizione con:

r = OP

r’ = O’P

mentre la distanza tra le origini é:

R = OO’

Risulta subito (somma vettoriale):

r = R + r’           …. (1)

Facciamo prima il caso più semplice, ossia i due sistemi traslano soltanto uno rispetto all’altro. Ciò non vuol dire, però, che O’ non possa accelerare rispetto a O, ossia che la sua velocità non sia variabile. Per adesso consideriamo il caso che trasli con velocità costante.

Possiamo derivare la (1) rispetto al tempo per trovare la formula che lega le velocità.

Nel caso di pura traslazione i versori unitari degli assi (freccette nere e rosse) restano quelli che sono (in modulo, direzione e verso), ossia coincidono per entrambi i sistemi. Ciò comporta una derivata semplicissima:

dr/dt = dR/dt + dr’/dt         …. (2)

v = V + v’                 …. (3)

Perché? Facile a provarsi dato che per un vettore s qualsiasi di versore u (costante per traslazione) si ha:

s = s u

derivando:

ds/dt = dsu/dt = uds/dt + sdu/dt = uds/dt = uv = v     …. (4)

du/dt = 0, ovviamente, dato che il versore è rimasto sempre uguale, come modulo, direzione e verso.

Se il moto, invece, è anche rotatorio, le cose si complicano dato che la derivata di un versore u (è ancora di modulo unitario, ma cambia direzione e verso) è un nuovo versore perpendicolare al primo. In particolare si dimostra che:

du/dt = ω Λ u           …. (5)

Dove ω è il vettore velocità angolare (regola della mano destra, ricordate…).

Per ottenere questa semplice relazione, basta dimostrare che la derivata di un versore (non costante in direzione e verso) è sempre un versore (unitario come modulo) ma con direzione perpendicolare al primo.

Facciamo il prodotto scalare di due versori ortogonali:

(u X u) = u² = costante

d(u X u)/dt  = d(u²)/dt = 0

ma la derivata si può anche scrivere:

d(u X u)/dt = u X du/dt + u X du/dt = 2 u X du/dt

Tuttavia, sappiamo che la derivata deve essere uguale a ZERO, da cui segue che

2 u X du/dt = 0

Ossia:

u X du/dt = 0

Ma se il prodotto scalare di due versori di modulo costate è uguale a zero essi devono essere perpendicolari. Ossia, se la rotazione (ω) avviene attorno a un’asse perpendicolare a entrambi si ha proprio che du/dt può essere scritto come la (5):

du/dt = ω Λ u 

La (5) diventa, per un vettore generico s di versore u:

ds/dt = d(su)/dt = uds/dt + sdu/dt = uds/dt  + sω Λ u = u v + ω Λ su = v + ω Λ s       …. (6)

Riprendiamo allora la (2):

dr/dt = dR/dt + dr’/dt

Tenendo conto della (6), si ottiene:

v = V + v’ + ω Λ r’                    …. (7)

Riflettiamoci un attimo, confrontando la (7) con (3).

v’ è la velocità del punto P nel sistema di riferimento S’.

V è la velocità dell’origine O’ di S’ rispetto all’origine O di S.

v è la velocità del punto P nel sistema di riferimento S.

Che cosa differenzia le due velocità v e v’? Un termine che dipende solo dalla traslazione e rotazione del sistema S’, ossia non dipende assolutamente dal moto del punto P. Questo concetto è fondamentale, anche se sembra estremamente ovvio.

Questo termine possiamo chiamarlo velocità di trascinamento v_T ed è dato da:

v_T = V + ω Λ r’

In parole molto semplici possiamo dire che questa è la velocità che avrebbe in S un punto fermo in S’, trascinato dal moto di S’. Infatti, inserendo v’ = 0 nella (7), la v diventa proprio v_T.

La (7), ovviamente, si trasforma nella (3) se non vi è rotazione. Ma, ancora più importante per noi, la (7) diventa:

 v = v’ + ω Λ r’       …. (8)

se O coincide con O’ e non vi è nessuna traslazione. In poche parole stiamo lavorando con due sistemi, in cui uno si muove di moto soltanto rotatorio rispetto all’altro.

Diciamo un’altra ovvietà, che è, comunque, molto interessante…

Consideriamo nuovamente un punto P fisso rispetto a S’. Cosa vediamo da S? Beh… semplicissimo. La v’ si annulla (il punto è fermo in S’) e, quindi, la v è uguale solo al termine di trascinamento ω Λ r’. Facciamoci aiutare dalla Fig. 2 per vedere cosa significa tutto ciò…

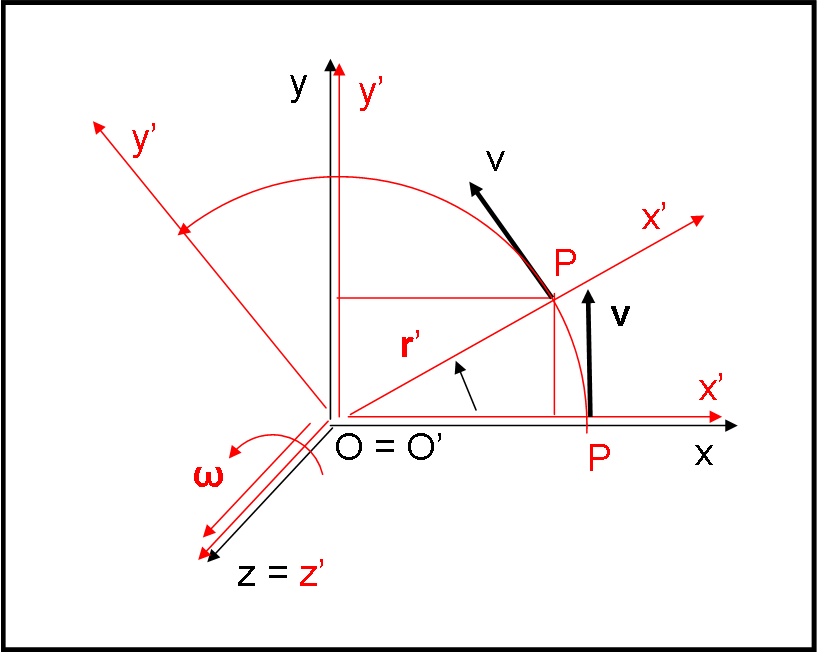
O coincide con O’ (nessuna traslazione, per cui possiamo anche fare coincidere le origini). Il sistema S’ ruota attorno all’asse z  con velocità angolare costante (vettore ω). La distanza r’ rimane costante (il punto P è fisso nel sistema S’: ad esempio, possiamo metterlo sull’asse x’). Abbiamo due vettori costanti in modulo e quindi deve essere costate in modulo anche il loro prodotto vettoriale, che altro non è che la velocità v di P nel sistema S.

Tuttavia, utilizzando la regola della mano destra possiamo facilmente vedere che il vettore v cambia continuamente direzione nel sistema S, dato che lo fa anche P. Insomma, O non può che dire che P si muove di moto circolare uniforme nel piano (x,y), e che v è la sua velocità tangenziale!

2. Accelerazione

Riprendiamo la relazione che esiste tra le velocità di un sistema rotante rispetto a uno fisso (8).

 v = v’ + ω Λ r’

Il prossimo passo è quello di trovare la relazione che esiste tra le accelerazioni

Nessun problema a derivare v. Essa vale a = dv/dt.

La derivata di v’  deve invece tener conto della (6) dato che il sistema sta ruotando, ossia:

dv’/dt = a’ + ω Λ v’

Ci resta ancora da derivare il prodotto vettoriale ω Λ r’

Esso vale, ovviamente:

d(ω Λ r’)/dt = dω/dt Λ r’ + ω Λ dr’/dt

Mettendo tutto assieme, si ottiene:

a = a’ + ω Λ v’ + dω/dt Λ r’ + ω Λ dr’/dt   …. (9)

Sappiamo, però dalla (6) che:

dr’/dt = v’ + ω Λ r’

Sostituendo questa relazione nella (9), si ha:

a = a’ + ω Λ v’ + dω/dt Λ r’ + ω Λ (v’ + ωΛr’)

a = a’ + ω Λ v’ + dω/dt Λ r’ + ω Λ v’ + ω Λ (ωΛr’)

a = a’ + dω/dt Λ r’ + 2ω Λ v’ + ω Λ (ω Λ r’)         …. (10)

Dove a’ è l’accelerazione nel sistema di riferimento rotante. Mettendola in evidenza, si ha:

a’ = a - dω/dt Λ r’ - 2ω Λ v’ - ω Λ (ω Λ r’)       …. (11)

Assumendo (per noi basta e avanza) che ω sia costante, si annulla il termine che contiene  la derivata di ω:

 a’ = a - 2ω Λ v’ - ω Λ (ω Λ r’)             …. (12)

Questa formula è fondamentale. Ci dice una cosa che ben conosciamo, ma che abbiamo ricavato solo attraverso il calcolo delle velocità e accelerazioni relative, in due sistemi di riferimento NON INERZIALI.

Nel sistema rotante, all’accelerazione esistente nel sistema fisso, per potere applicare le leggi della dinamica, è necessario introdurre due accelerazioni particolari: una è proprio l’accelerazione centrifuga, ossia il termine             -ωΛ(ωΛr’). Infatti, se v’ fosse uguale a zero (il punto fosse fisso nel sistema di riferimento rotante) avremmo che questa è l’unica accelerazione che bisogna aggiungere all’accelerazione esistente nel sistema fisso. Quest'ultima accelerazione è quella centripeta e, quindi, il termine - ω Λ (ωΛr’) è proprio quella che tiene il punto fisso nel suo sistema rotante.

Se, però, v’ non è uguale a zero (ossia il punto si sposta anche nel sistema di riferimento), deve entrare in ballo anche un’accelerazione aggiuntiva (che non viene annullata) e che è sempre perpendicolare alla direzione del moto. Questa non è altro che l’accelerazione di Coriolis, libera di agire e di essere ben visibile.

Moltiplicando tutte le grandezze per la massa M del corpo in movimento, si ottiene la relazione tra le forze vere e le forze fittizie, ossia quelle legate ai termini che fanno differire le due accelerazioni.

Fino  a qui abbiamo eseguito alcune semplificazioni, una fra tutte quella di far coincidere le origini dei due sistemi. In realtà, ci saremmo dovuti “portare dietro” un altro termine aggiuntivo, ma estremamente facile da tenere in conto. OO’ avrebbe avuto una velocità V e un’accelerazione A.

Come riepilogo, scriviamo, allora, le tre relazioni, complete di traslazione, ma con velocità angolare costante:

r = R + r’

v = V + v’ + ωΛr’

a =  A + a’ + 2ω Λ v’ + ω Λ (ωΛr’)          …. (13)

A seconda delle ipotesi di partenza sul moto di un sistema rispetto all’altro, le tre relazioni si semplificano di conseguenza.

Prendiamo il caso più classico: Le origini non coincidono, ossia OO’ è diverso da zero. Ancora più importante il fatto che O’ si muova rispetto a O con velocità costante V. Il sistema mantiene gli stessi versori, ossia non vi è rotazione. Ne segue che ω = 0. Le relazioni diventano:

r = R + r’

v = V + v’

a =  a’

Esattamente le condizioni che definiscono due sistemi inerziali.

Se, invece, la velocità di O’ fosse  variabile, avremmo:

r = R + r’

v = V + v’

a =  A + a’

E via dicendo …

Per lo studio dei sistemi rotanti senza traslazione e con O = O’(quelli che c’interessano per vedere gli effetti della forza di Coriolis) possiamo tornare alle relazioni che abbiamo ricavato nell’articolo:

r = r’

v = v’ + ω Λ r’

a =  a’ + 2ω Λ v’ + ω Λ (ω Λ r’)             .... (14)

Notiamo un fatto molto importante: la forza di Coriolis non è mai sola, ma è sempre accompagnata da quella centrifuga, mentre non è vero il viceversa. Inoltre, ribadiamolo ancora, la forza di Coriolis nasce solo quando si ha un movimento del corpo in uno dei due sistemi di riferimento. Tuttavia, a seconda che si muova in quello rotante o in quello fisso, gli effetti sono diversi… cosa che spesso viene male interpretata…

Le relazioni precedenti porterebbero alle equazioni del moto,  come quelle di pura traslazione. Noi, però, ci limiteremo a descrivere i vari effetti graficamente, sapendo ormai bene quali forze agiscono, siano esse vere o “fittizie”.

 

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis