Categorie: Matematica
Tags: aree negative formula di Gauss laccio da scarpa prodotto vettoriale quiz soluzione
Scritto da: Vincenzo Zappalà
Commenti:2
Dal laccio di scarpa alle aree negative **/***
Innanzitutto, un bravo particolare a Leandro che in qualche modo (magari non il più semplice) è riuscito ad allacciare la scarpa... D'altra parte nel poco conosciuto metodo per il calcolo dell'area di un triangolo (e di un poligono qualsiasi) c'è la mano di Gauss.
In realtà il metodo "laccio da scarpa" prende anche il nome di formula di Gauss, ma, in realtà era già stato proposto da Albrecht Ludwig Friedrich Meister (1724–1788) nel 1769 e solo nel 1795 da Carl Friedrich Gauss. Come al solito, la fama gioca a vantaggio di chi ce l'ha (e se l'è comunque più che meritata).
Il modo, forse più semplice, per arrivare alla formula finale è quello seguito da Leandro. Tuttavia, vedremo che una visione un po' diversa ci permetterà di utilizzare i vettori, il loro prodotto e le aree ... negative. Un approccio sicuramente utile per molte altre applicazioni. Iniziamo, lavorando sul piano cartesiano, calcolando le aree in modo puramente geometrico.
Metodo geometrico **
Sia ABC il nostro triangolo. Costruiamo il rettangolo che passa per i tre vertici come illustrato in Fig. 1
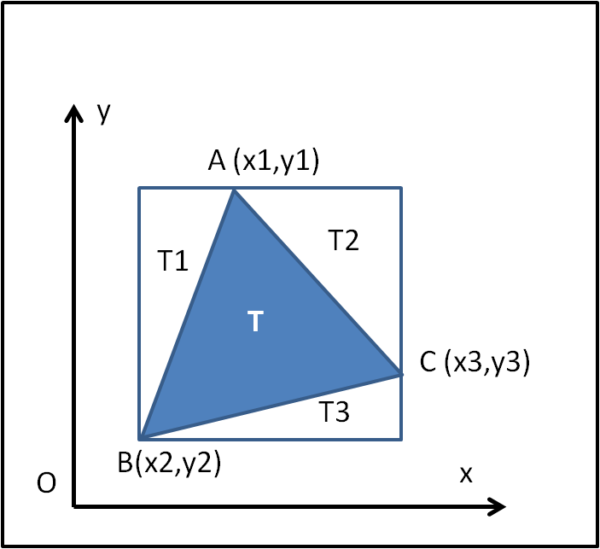
L'area del nostro triangolo T è uguale all'area del rettangolo R meno le aree dei triangoli T1, T2 e T3. In breve, attraverso tanti termini, tutti però estremamente banali:
AT = AR - AT1 - AT2 - AT3
AR = (x3 - x2)(y1 - y2) = x3y1 - x3y2 - x2y1 + x2y2
AT1 = 1/2((x1 - x2)(y1 - y2)) = 1/2(x1y1 - x1y2 - x2y1 + x2y2)
AT2 = 1/2((x3-x1)(y1 - y3) = 1/2(x3y1 - x3y3 - x1y1 + x1y3)
AT3 = 1/2((x3 - x2)(y3 - y2)) = 1/2( x3y3 - x3y2 - x2y3 + x2y2)
AT = x3y1 - x3y2 - x2y1 + x2y2 -1/2(x1y1 - x1y2 - x2y1 + x2y2) - 1/2(x3y1 - x3y3 - x1y1 + x1y3) -1/2( x3y3 - x3y2 - x2y3 + x2y2)
AT = 1/2 (2x3y1 - 2x3y2 - 2x2y1 + 2x2y2 - (x1y1 - x1y2 - x2y1 + x2y2) - (x3y1 - x3y3 - x1y1 + x1y3) - (x3y3 - x3y2 - x2y3 + x2y2)
AT = 1/2 (2x3y1 - 2x3y2 - 2x2y1 + 2x2y2 - x1y1 + x1y2 + x2y1 - x2y2 - x3y1 + x3y3 + x1y1 - x1y3 - x3y3 + x3y2 + x2y3 - x2y2)
AT = 1/2 (x3y1 - x3y2 - x2y1 + x1y2 - x1y3 + x2y3)
AT = 1/2 (x1y2 + x2y3+ x3y1 - x1y3 - x3y2 - x2y1)
Questa è la formula risolvente che può essere estesa a qualsiasi poligono concavo o convesso (ma non solo, vedremo) e può essere rappresentata con il famoso laccio da scarpa. Per ottenerlo scriviamo in colonna le coppie di coordinate cartesiane dei vari vertici, aggiungendo alla fine nuovamente la prima coppia:

La "scarpa" è pronta e ora basta far passare il laccio dall'alto verso il basso (moltiplicando tra loro le coordinate) seguendo le frecce rosse e, poi, tornare indietro dal basso verso l'alto seguendo le linee blu. Quelle in discesa vanno considerate positive e quelle in salita negative.
Otteniamo proprio:
x1y2 + x2y3 + x3y1 - x1y3 - x3y2 - x2y1
Infine si moltiplica tutto per 1/2.
Il laccio ha eseguito il suo compito, la scarpa non si muove più e l'area di qualsiasi poligono viene calcolata perfettamente!
Metodo vettoriale ***
Vediamo di arrivare alla formula finale attraverso il calcolo vettoriale. In particolare richiamiamo il prodotto vettoriale che avevamo introdotto a proposito del momento angolare, ricordando soltanto che il prodotto vettoriale è ancora un vettore che ha un modulo, una direzione e un verso. Il suo modulo è dato dal prodotto dei moduli dei due vettori moltiplicato per il seno dell'angolo compreso; la direzione è quella perpendicolare al piano dei due vettori; il verso è definito dalla regola della mano destra.
Quest'ultima caratteristica può essere facilmente stabilita dando un ordine ai due vettori (vettore UNO e vettore DUE) e applicare il vettore DUE sulla punta del vettore UNO: se la rotazione va in verso antiorario, il verso del vettore finale va verso l'alto (verso positivo), se la rotazione va in verso orario, il verso del vettore finale va verso il basso (verso negativo). Meglio di tante parole vale sicuramente la Fig. 2, ricordando anche che allo stesso risultato si arriva pensando a una vite che si avvita o si svita...

Quanto vale il prodotto vettoriale? Come già detto esso si può scrivere come il prodotto dei moduli dei due vettori moltiplicato per il seno dell'angolo compreso tra 1 e 2. Nel caso a sinistra della Fig. 2 il seno è positivo dato che l'angolo tra 1 e 2 è minore di 90°, mentre nel caso a destra il seno è negativo dato che l'angolo tra 1 e 2 è maggiore di 180°. Guardando le cose in questo modo, torna perfettamente anche il segno positivo o negativo del prodotto vettoriale.
Consideriamo il caso di sinistra e poniamoci nel piano dei due vettori v1 e v2 (Fig. 3)

Eseguiamo il prodotto vettoriale e consideriamone il modulo
|v1 ∧ v2| = v1 v2 sen φ
Ciò che abbiamo scritto, però, non è altro che l'area del parallelepipedo OABC, dato che v1 è la sua base e v2 sen φ la sua altezza. Ne segue che il prodotto vettoriale rappresenta anche un'area e, in particolare, se la dividiamo per due, otteniamo l'area del triangolo OAC. In tal modo, tenendo conto dell'ordine dei punti, possiamo dimostrare vettorialmente la validità della formula del "laccio da scarpa".
Ricordiamo la formula (13) dell'articolo dove affrontiamo il calcolo del prodotto vettoriale. Essa ci dice che l'area è proprio la componente del vettore parallelo al versore k (perpendicolare al piano del triangolo) e vale:
v1 Λ v2 = x1 y2 k - y1 x2 k = (x1 y2 - y1 x2) k
Ovviamente le componenti del vettore v1 sono x1 e y1, quelle del vettore v2 sono x2 e y2 e via dicendo.
Consideriamo la Fig. 4 con i tre vettori v1, v2 e v3 che corrispondono ai punti A, B e C, rispettivamente.

L'importante è avere cura di porre i vertici in ordine antiorario, ossia andando da A a B a C si deve andare in verso antiorario; in tal modo anche l'ordine dei vettori v1, v2 e v3 va in modo concorde: il primo vettore è v1 = OA, v2 = OB e v3 = OC
Eseguiamo i prodotti vettoriali tra le coppie di vettori
v1 Λ v2 = (x1 y2 - x2y1) k 2 volte area OAB
v2 Λ v3 = (x2y3 - x3y2) k 2 volte area OBC
v3 Λ v1 = (x3y1 - x1y3) k 2 volta area OCA
A questo punto ci basta sommare le tre aree (e dividere per 2) per ottenere nuovamente la formula a laccio di scarpa
AT = 1/2 (x1y2 + x2y3+ x3y1 - x1y3 - x3y2 - x2y1)
Cosa abbiamo ottenuto? Una conclusione che potrebbe sembrare assurda dato che abbiamo eseguito la somma delle aree di tre triangoli che appare ben maggiore dell'area cercata (quella di ABC). E invece no! Considerando le coppie di vettori con il giusto ordine (v1 e v2, v2 e v3, v3 e v1) notiamo che l'area ottenuta da v3 Λ v1 è positiva (si passa da C verso A in senso antiorario), mentre le atre due sono negative (si passa da A a B in e da B a C in senso orario). In pratica, all'area del triangolo OCA abbiamo sottratto le aree dei triangoli OAB e OBC.
Le aree con segno **
Lasciamo il laccio da scarpa e cerchiamo di generalizzare quanto appena detto in modo più generale. Introduciamo il simbolo S per definire un area con un segno e il simbolo A per definirla in valore assoluto.
In altre parole:
S(ABC) = A(ABC) se ABC vanno in senso antiorario
S(ABC) = - A(ABC) se ABC vanno in senso orario ... (1)
Possiamo allora dire che preso un punto P qualsiasi, interno od esterno a un triangolo ABC, l'area del triangolo può essere sempre scritta come:
S(ABC) = S(PAB) + S(PBC) + S(PCA)
La dimostrazione è ormai ovvia in entrambi i casi.
Consideriamo P interno come mostra la Fig. 5

L'area del triangolo ABC è data dalla somma delle aree dei tre triangoli PAB, PBC e PCA. Possiamo scrivere:
A(ABC) = A(PAB) + A(PBC) + A(PCA)
Notiamo, però, che tutte le aree che abbiamo definito sono POSITIVE, dato che l'ordine dei loro vertici è quello antiorario, per cui possiamo scrivere:
S(ABC) = S(PAB) + S(PBC) + S(PCA)
Dimostrazione veramente ovvia.
Consideriamo, adesso, P esterno come mostra la Fig. 6

L'area del triangolo ABC è adesso data dalla somma delle aree di PAB e PBC meno l'area del triangolo PCA.
A(ABC) = A(PAB) + A(PBC) - A(PCA)
Tuttavia, mentre lee aree di ABC e quelle di PAB e PBC corrispondono a triangoli con i vertici che seguono il verso antiorario e quindi sono uguali alle rispettive S, l'area di PCA corrisponde a un triangolo con i vertici che vanno in senso orario. Per la (1) segue allora che - A(PCA) vale proprio S(PCA).
Si ottiene, perciò, nuovamente che:
S(ABC) = S(PAB) + S(PBC) + S(PCA)
Ciò che ho dimostrato sembra proprio un'ovvietà, ma ci permette di ottenere l'area di qualsiasi poligono concavo o convesso, sommando aree triangolari con segno, dato che l'ordine dei vertici impone direttamente la loro addizione o sottrazione. Volendo esagerare nella spiegazione proviamo con un pentagono concavo ABCDE, mostrato in Fig. 7.
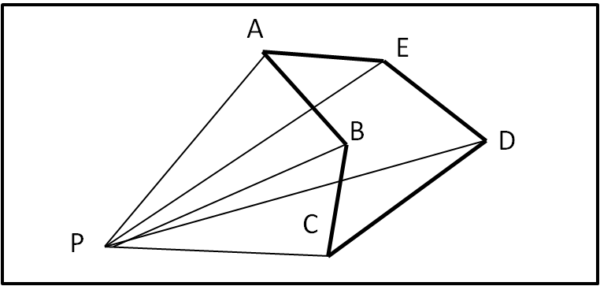
Scriviamo pure la formula definita precedentemente:
S(ABCDE) = S(PAB) + S(PBC) + S(PCD) + S(PDE) + S(PEA)
Controlliamo il verso dei vari vertici
PAB orario, PBC orario, PCD antiorario, PDE antiorario, PEA antiorario
Ne segue che:
A(ABCDE) = - A(PAB) - A(PBC) + A(PCD) + A(PDE) + A(PEA)
La formula funziona perfettamente dato che l'area del pentagono risulta essere proprio la somma delle aree dei tre triangoli PCD, PDE e PEA a cui si sottrare l'area di PAB e PBC.
A questo punto abbiamo la possibilità di risolvere un interessante problema geometrico che vedremo la prossima volta.






2 commenti
Continui ad aprirmi nuove finestre sul mondo della matematica di cui neppure ne intuivo l'esistenza. No, a dire il vero, il metodo geometrico faceva già parte delle mie capacità e l'avevo subito dato per scontato, senza fare calcoli, restandomene seduto in divano. Ma i lacci da scarpe e tanto più il metodo vettoriale, nella loro estrema semplicità mi hanno profondamente colpito. Una sola curiosità: queste soluzioni fanno parte del comune bagaglio di un laureato in matematica? Si studiano regolarmente e con metodo all'università o risultano dalla cultura generale che un matematico acquisisce (o non acquisisce) successivamente?
caro Albertone,
mi fa veramente piacere che queste "chicche" geometriche piacciano anche a te (io ne sono innamorato...). No, non fanno parte del bagaglio normale, ma si scoprono proprio per la curiosità tipica dei matematici verso soluzioni eleganti e non comuni. Io le ho scoperte il più delle volte per caso. Certo è che sarebbe molto bello se venissero introdotte nei corsi di matematica per stimolare l'interesse verso una materia che tutto è meno che noiosa e priva di fantasia.
Tra poco inserirò un quiz che dovresti provare a risolvere con quanto acquisito in questo articolo: l'eleganza e la semplicità brillano veramente!