Nel precedente articolo, che potete rileggere QUI, ho introdotto il concetto di parametri direttori di una retta nel piano. In questo estendo il concetto al piano e alla retta nello spazio. Passiamo, quindi, nel riferimento cartesiano dello spazio.

Parametri direttori di un piano

Si definiscono parametri direttori di un piano le componenti lungo i tre assi cartesiani di uno degli infiniti vettori perpendicolari al piano.

Consideriamo l'equazione del piano  

ax+by+cz+d=0    (con a, b, c, d coefficienti reali)

Siano dati due punti A (xa, ya, za)  e B (xb, yb, zb) appartenenti al piano . Facciamo riferimento alla figura n.2 :

Le loro coordinate devono soddisfare l'equazione del piano, quindi:

punto B:

punto A:

sottraendo membro a membro ottengo

Ciò che sta a primo membro posso vederlo come prodotto scalare tra i vettori v(a,b,c) e AB(xb-xa,yb-ya,zb-za). Il prodotto scalare tra due vettori, infatti, analiticamente è dato dalla somma dei prodotti delle rispettive componenti. Essendo, quindi, il suddetto prodotto scalare pari a zero, se ne deduce, per definizione di prodotto scalare tra vettori, che il vettore v (a,b,c) (diverso dal vettore nullo) è perpendicolare al vettore AB (diverso dal vettore nullo). Ma il vettore AB , congiungendo due punti del piano , appartiene al piano, quindi è ad esso banalmente parallelo. In definitiva, le componenti del vettore v sono proprio i parametri direttori del piano . Dunque, data l'equazione del piano, i suoi parametri direttori si individuano subito, semplicemente leggendo l'equazione del piano,  e sono (a, b, c) ! Se, eventualmente, nell'equazione del piano non dovesse comparire la x oppure la y oppure la z, allora i relativi coefficienti saranno pari a zero.

Qualche esempio numerico. Sia dato il piano di equazione x+2y-3z+2=0 . In questo caso abbiamo a=1, b=2, c=-3. Una terna di parametri direttori del piano è dunque (1,2,-3). Fatto ! Anche ora, per lo stesso motivo visto per la retta, possiamo moltiplicare i tre parametri per uno stesso numero diverso da zero e ottenere un'altra terna di parametri direttori.

Un altro esempio. Piano di equazione z=0. In tal caso nell'equazione non compaiono né la x né la y. In questo caso, quindi, a=0, b=0 e c=1. Una terna di parametri direttori del piano sarà allora (0,0,1) . Non a caso, queste sono le componenti sui tre assi cartesiani del versore k, ossia del vettore di modulo unitario e direzione perpendicolare al piano xy. Infatti il piano z=0 è proprio quello cartesiano xy.

Ricordiamo, quindi: quando ci troviamo difronte l'equazione di un piano, i coefficienti a, b, c dell'equazione sono le componenti di un vettore perpendicolare al piano.

Evidenzio qui la differenza tra parametri direttori della retta e parametri direttori del piano. Nel caso della retta, essi individuano la direzione della retta. Nel caso del piano individuano la direzione perpendicolare al piano.

Parametri direttori di una retta nello spazio

Come illustrato nei precedenti articoli, una retta nello spazio va vista come intersezione di due piani. Essa, dunque, viene individuata analiticamente da un sistema di due equazioni, ossia quelle dei due piani che si intersecano nella retta. Siano, dunque, date le equazioni di tali due piani:

piano  :

piano :

I due piani , per quanto detto nei paragrafi precedenti, avranno come possibile terna di parametri direttori (a1, b1, c1)  e (a2, b2, c2) rispettivamente. Per come sono stati definiti i parametri direttori di un piano, tali terne rappresentano ciascuna le componenti sui tre assi cartesiani di un vettore perpendicolare al piano. Chiamo v1 il vettore perpendicolare al piano  e v2 il vettore perpendicolare al piano . Poiché la retta r definita dalle due suddette equazioni appartiene sia a  sia a , essa risulterà perpendicolare sia al vettore v1 sia al vettore v2. Noi cerchiamo i parametri direttori della retta, ossia le componenti sui tre assi cartesiani di un vettore r parallelo alla retta. Tale vettore, per quanto sopra, sarà perpendicolare sia a v1 sia a v2. Dal calcolo vettoriale sappiamo che per trovare un vettore che sia perpendicolare a due vettori dati, basta fare il prodotto vettoriale tra questi ultimi. Ossia:

                    ( oppure        a seconda del simbolo adottato per indicare il prodotto vettoriale)

Sempre dal calcolo vettoriale, sappiamo che tale prodotto si calcola agevolmente considerando il determinante della matrice 3x3

dove i , j e k sono i versori dei tre assi.

Quindi, a conti fatti:

Chi volesse approfondire il calcolo analitico del prodotto vettoriale, può rileggere QUI.

Le componenti sui tre assi cartesiani del vettore r , cioè i parametri direttori della retta, saranno quindi

Basta, dunque, leggere le equazioni dei due piani e fare delle semplici moltiplicazioni e sottrazioni. Vediamo degli esempi. In tutte le figure seguenti, la retta individuata dai due piani è di colore nero.

Esempio 1

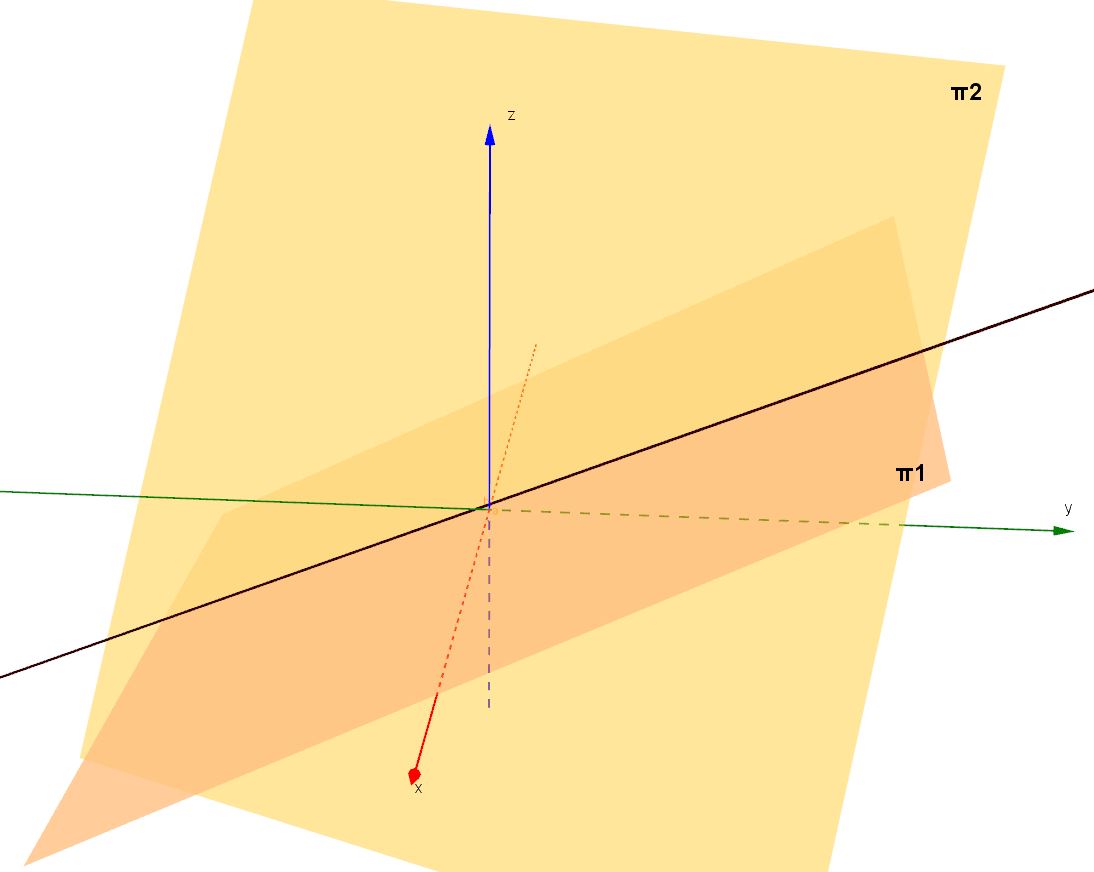
Sia data la retta definita nello spazio dalle equazioni
:  y-2z+1=0

: 2x-y+z=0

Il piano   ha parametri direttori (0,1,-2) . Il piano  ha parametri direttori (2,-1,1). Risulta utile scrivere tali due terne una sopra l'altra, così da avere incolonnati i sei  parametri:

(0, 1, -2)

(2, -1, 1)

I parametri direttori della retta saranno, quindi:

 = (1)x(1)-(-1)x(-2) = 1-2=-1

 = (2)x(-2)-(0)x(1) = -4-0=-4

 = (0)x(-1)-(2)x(1) = 0-2 = -2

Potremmo, volendo, moltiplicare tutto per (-1) ottenendo una nuova terna di parametri direttori (1, 4, 2).

 

Esempio 2

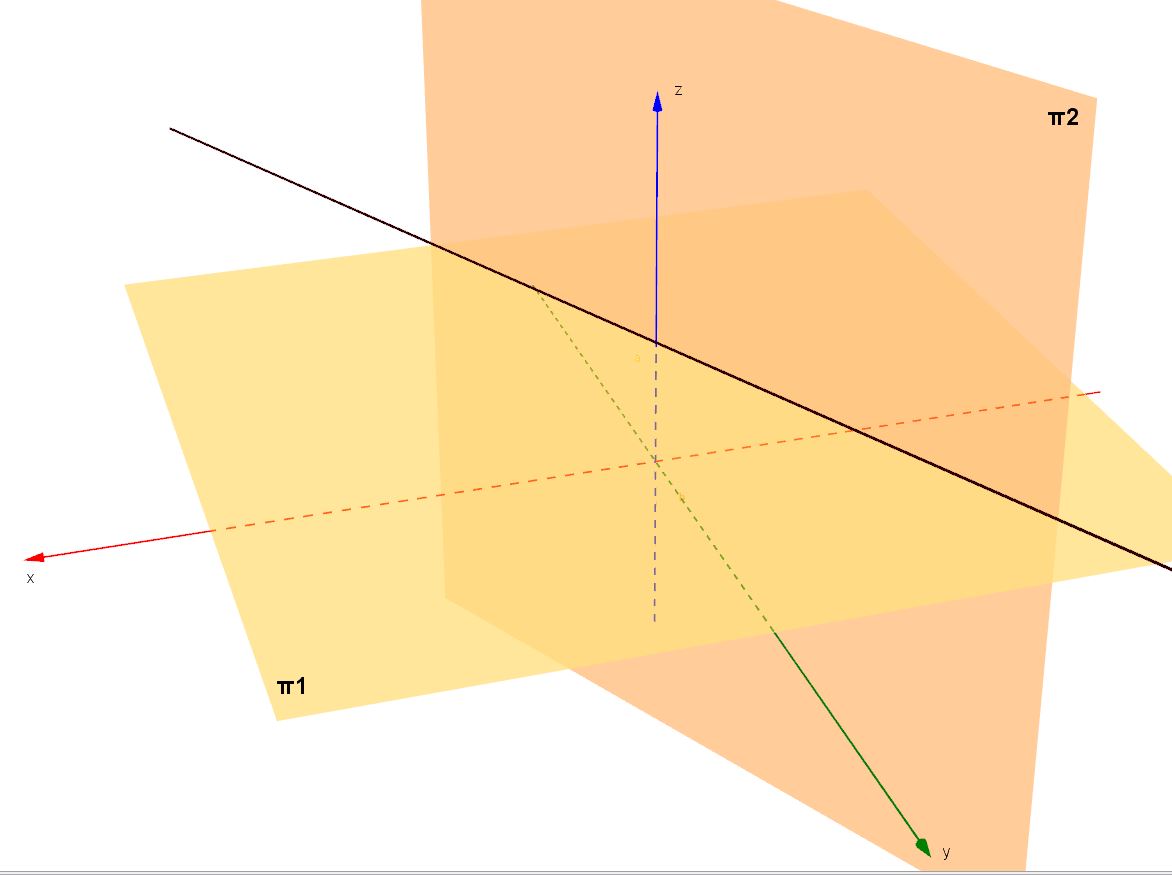
Sia data la retta definita nello spazio dalle equazioni

:  z-2=0

:  2x+y=0

Parametri direttori del piano  : (0,0, 1). Parametri direttori del piano : (2, 1, 0) .

Incolonniamo i parametri:

(0,0, 1)

(2, 1, 0)

Parametri direttori della retta:

 = (0)x(0)-(1)x(1) = 0-1=-1

 = (2)x(1)-(0)x(0) = 2-0=2

 = (0)x(1)-(2)x(0) = 0-0 = 0

 

Esempio 3

Sia data la retta definita nello spazio dalle equazioni

:  x=0 ---> parametri direttori (1, 0, 0)

:  z+1=0 ---> parametri direttori (0, 0, 1)

(1, 0, 0)

(0, 0, 1)

Parametri direttori della retta:

 = (0)x(1)-(0)x(0) = 0-0= 0

 = (0)x(0)-(1)x(1) = 0-1= -1

 = (1)x(0)-(0)x(0) = 0-0 = 0

 

Esempio 4

Sia data la retta definita nello spazio dalle equazioni

:  x-3y+z=0 ---> parametri direttori (1, -3, 1)

:  2x+y-z+1=0 ---> parametri direttori (2, 1, -1)

(1, -3, 1)

(2, 1, -1)

Parametri direttori della retta:

 = (-3)x(-1)-(1)x(1) = 3-1= 2

 = (2)x(1)-(1)x(-1) = 2+1= 3

 = (1)x(1)-(2)x(-3) = 1+6 = 7

 

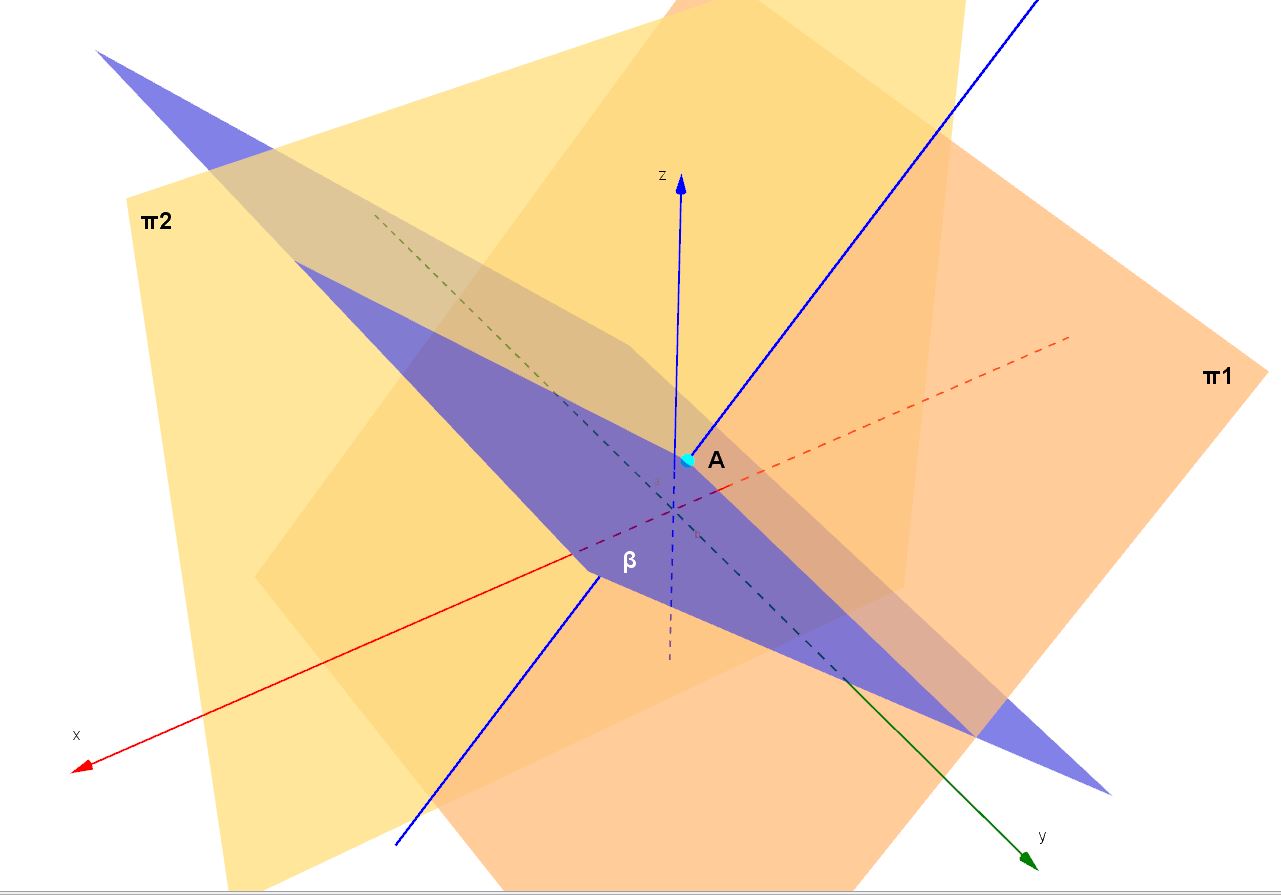
L'efficacia dei parametri direttori nella soluzione di problemi di geometria dello spazio si intuisce dal seguente esempio di applicazione. Supponiamo di avere una retta nello spazio definita dalle due equazioni:

 : y+2=0   --->   parametri direttori  (0, 1, 0)

 : x+z+2=0 ---> parametri direttori (1, 0, 1)

Sia dato un suo punto A di coordinate (-2, -2,0). Determinare l'equazione del piano  passante per A e perpendicolare alla retta.

Sappiamo ormai ricavarci i  parametri direttori della retta:

(0, 1, 0)

(1, 0, 1)

 = (1)x(1)-(0)x(0) = 1-0= 1

 = (1)x(0)-(0)x(1) = 0-0= 0

 = (0)x(0)-(1)x(1) = 0-1 = -1

Poiché i parametri direttori di un piano, per definizione, sono le componenti di un vettore perpendicolare al piano, e abbiamo visto che una terna di tali componenti è costituita proprio dai coefficienti dell'equazione del piano, allora , per trovare un piano perpendicolare ad una retta data, di cui si siano già determinati i parametri direttori, basta mettere come coefficienti nell'equazione del piano cercato proprio i parametri direttori della retta. Quindi:

1*x+0*y-1*z+d=0 ---> x-z+d=0

Resta da calcolare il coefficiente d. A questo scopo, consideriamo che il piano deve passare per A, quindi (sostituendo le coordinate del punto A nell'equazione del piano):

-2+d=0 ---> d=2

L'equazione del piano  è dunque:

x-z+2=0

Naturalmente, l'utilità dei parametri direttori della retta nello spazio emerge maggiormente nel caso in cui la retta sia l'intersezione di due piani generici, e quindi non è facile intuirne subito l'andamento nello spazio. E' chiaro che se, invece, i due piani che intersecandosi generano la nostra retta sono piani semplici, come ad esempio il piano xy (equazione z=0) e il piano x=5 , si riesce a capire velocemente che la retta giacerà sul piano xy e sarà parallela all'asse y , quindi una sua terna di parametri direttori potrà essere (0,1,0), cioè quella delle componenti del versore j. Ma il metodo dei parametri direttori è assolutamente generale , quindi ci consente di tirarci fuori dai guai anche in casi di rette comunque disposte nello spazio.

A questo proposito, vedremo nei prossimi articoli come questo avvenga, per esempio, nel caso si voglia determinare una superficie di rotazione, ottenuta facendo ruotare una data curva attorno ad una generica retta dello spazio. Una volta conosciuto il metodo per determinare l'equazione di una superficie di rotazione (illustrato graficamente nell'immagine animata seguente) , ricaveremo, utilizzando i parametri direttori della retta nello spazio,  non solo superfici di rotazione con asse perpendicolare ad uno dei piani coordinati (caso più semplice), ma anche quelle con asse comunque disposto nello spazio.