Categorie: Fisica classica Matematica
Tags: area parallelogramma componenti modulo momento angolare prodotto vettoriale regola mano destra versori
Scritto da: Vincenzo Zappalà
Commenti:3
Momento angolare & Co. 3: basta avvitare o svitare **/***/****
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo
Il prodotto scalare che abbiamo descritto nell’articolo precedente può essere considerato un’azione “statica”. Mi spiego meglio. Abbiamo proiettato un vettore su un altro (come se avessimo tirato un fendente) e poi ci siamo limitati a valutare il punteggio finale, ossia il prodotto tra la proiezione del primo vettore (componente) e il modulo del secondo. Un colpo e via! Non per niente il risultato è stata una grandezza scalare.
I vettori, però, sono grandezze dinamiche, in cui la direzione e il verso (la punta della freccia) indicano una propensione al movimento. Nel prodotto scalare, l’unico movimento è stata una proiezione (un fendente) che ha prodotto un numero e niente più. In altre parole: abbiamo calcolato la componente di un vettore lungo la direzione dell’altro vettore e poi ci siamo limitati a moltiplicare due lunghezze che giacevano sulla stessa retta. Il verso dei vettori è solo servito a vedere se il prodotto era positivo o negativo.
Due vettori per ottenere solo uno scalare… sembra quasi uno spreco. No, no, stiamo attenti a giudicare troppo velocemente le grandezze fisiche, dato che il lavoro, e di conseguenza anche l’energia di cui il lavoro è una differenza, nascono proprio in questo modo. Tuttavia, coloro che amano i colpi di scherma più articolati e dinamici, troveranno pane per i loro denti nel prodotto vettoriale. Ricordiamo ancora che i prodotti tra vettori sono di due tipi: il prodotto scalare (che già abbiamo conosciuto) e il prodotto vettoriale.
Attacco e difesa
Bene, posso subito dire che il risultato di un prodotto vettoriale è ancora un vettore, completamente diverso da quelli di partenza. Essendo un vettore, dobbiamo riuscire a definire molto bene il suo modulo, la sua direzione e il suo verso. Per rimanere ancora un attimo nel campo della scherma, il prodotto vettoriale vede le due spade agire insieme, ognuna con la sua prerogativa. Una cerca di colpire, ma l’altra devia la lama avversaria e il risultato è una lama puntata lontano dal bersaglio: attacco e difesa insomma, una specie di … presa di ferro.
Concludiamo qua l'ormai troppo “forzato” paragone con la nobile arte della scherma e dedichiamoci a una descrizione più matematica e geometrica. Userò, però, una trattazione che credo sia ben poco seguita sui libri, ma che pone già le basi per il personaggio principale delle nostre “lezioni”: il momento angolare. Normalmente, il prodotto vettoriale si definisce attraverso un paio di regole che vanno più o meno digerite per quello che sono, comportando un certo sforzo mnemonico. Una metodo che a me piace poco… e, quindi, a scapito di una serie più lunga di passaggi, vorrei mettere in luce la dinamicità dell’intera azione.
Andiamo, quindi, per gradi, cominciando dal modulo del vettore prodotto vettoriale. Questo modulo ha anche un significato geometrico non certo trascurabile, che è spesso usato in geometria superiore.
Un modulo … perpendicolare
Per calcolare il modulo possiamo tranquillamente rimanere su un piano. L’operazione da svolgere è mostrata in Fig. 14. Come al solito abbiamo i nostri due vettori v e u. Per il momento, non abbiamo nessun vincolo sul loro ordine di entrata. Per calcolare il modulo entrambi possono svolgere la stessa procedura. Consideriamo, prima, v.
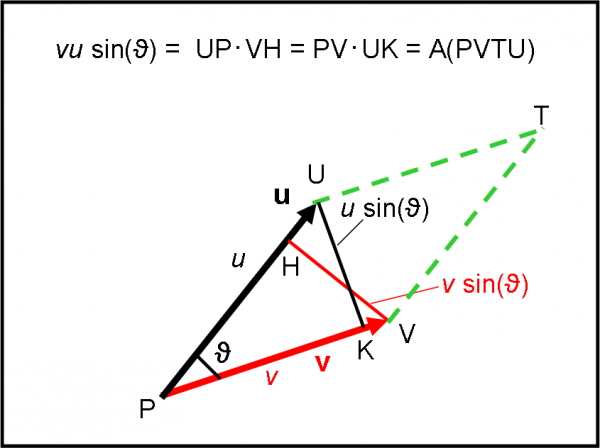
L’operazione non è molto diversa da quella eseguita nel prodotto scalare, ossia bisogna proiettare il vettore v sul vettore u (ossia tracciare su u la perpendicolare dalla punta di v) in modo da ottenere il solito triangolo rettangolo PHV. La volta scorsa ci eravamo interessati del segmento PH (ricordate?). Questa volta, invece, siamo interessati a VH. Esso è uno scalare, una lunghezza, perpendicolare al vettore u. Le due “spade” formano un angolo retto. Tuttavia, ciò che dobbiamo fare è proprio moltiplicare VH per il modulo di u (u= PU).
Non sto a perdere tempo a scrivere la moltiplicazione in questo modo, ma aggiungo subito (e lo dovreste sapere bene) che VH non è altro che il modulo di v moltiplicato per il seno dell’angolo compreso tra i due vettori (considerato sempre positivo e compreso tra 0 e 180°), ossia:
VH = v sin (ϑ)
Possiamo concludere che il modulo del vettore “prodotto vettoriale” è dato da:
modulo prodotto vettoriale = vu sin (ϑ).
Come avevo già anticipato, possiamo tranquillamente invertire i compiti dei due vettori. Possiamo, infatti, tracciare la perpendicolare dalla punta del vettore u sulla direzione del vettore v, ottenendo così il segmento UK = u sin (ϑ) e poi moltiplicarlo per il modulo v di v. Otteniamo lo stesso risultato di prima, ossia:
uv sin (ϑ).
Abbiamo dimostrato che possiamo sia usare la proiezione di u su v che quella di v su u, ma il modulo del nostro vettore finale non cambia. In termini pratici, possiamo concludere che il modulo del vettore prodotto vettoriale di due vettori u e v, è dato dal prodotto dei due moduli u e v moltiplicato per il seno dell’angolo compreso. Ricordiamoci che l’angolo deve essere sempre considerato tra 0 e 180° (mai negativo).
A questo punto, introduciamo il simbolo che identifica il prodotto vettoriale (una v rovesciata) e indichiamo il suo modulo come il vettore compreso tra due barrette verticali. Questa scrittura ci dice che stiamo lavorando con un numero scalare sempre positivo, in particolare con il modulo di quel vettore. In formula:
|v Λ u| = |u Λ v| = uv sin (ϑ)
L’uguaglianza iniziale (potere invertire l’ordine dei vettori) l’abbiamo potuta scrivere dato che abbiamo ottenuto lo stesso risultato sia partendo con v che partendo con u. Tuttavia, essa vale SOLO per il modulo e non per il vettore finale: stiamo bene attenti!
Area di un parallelogramma
Prima di procedere, guardiamo un attimo che cosa ci permette di calcolare il modulo del prodotto vettoriale. E’ immediato dedurlo attraverso la Fig. 14. Costruiamo il parallelogramma che ha per lati i due vettori, ossia PUTV (lo conosciamo bene… è quello della famosa regola del parallelogramma). Quanto vale l’area di un parallelogramma? Dovreste saperlo tutti: base per altezza. Una base del parallelogramma è sicuramente PV e la su altezza relativa è UK. Ma il prodotto PV per UK non è altro che il modulo del nostro prodotto vettoriale. Lo stesso risultato si ottiene, ovviamente, moltiplicando l’altra base (UP) per la sua altezza (VH), che da nuovamente il modulo del prodotto vettoriale. Concludiamo, dicendo che il modulo del prodotto vettoriale di due vettori v e u è uguale al parallelogramma costruito sui due vettori.
Quando va a zero il modulo del prodotto vettoriale? Semplicissimo: o quando è zero uno dei due vettori o quando i due vettori hanno la stessa direzione (l’angolo ϑ va a zero e quindi anche il suo seno). Cosa succede, invece, se i due vettori sono perpendicolari? Si ottiene il valore massimo del prodotto (sin (90) = 1) ossia uv.
Vettori che girano
Bene, nel caso del prodotto scalare, a questo punto, avevamo già finito… adesso, invece, abbiamo appena cominciato. Ora c’è da stare molto attenti. Qualcuno si aspetterà la regola della “mano destra” e invece la introdurrò solo alla fine. Preferisco usare un approccio molto più istruttivo per il prosieguo verso il momento angolare. Consideriamo la Fig. 15a.
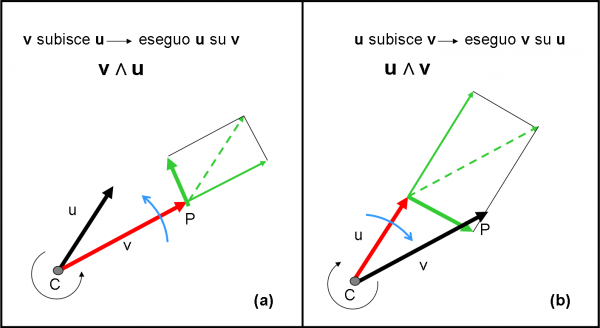
Da ora in poi dobbiamo sempre stare molto attenti a quale vettore compare per primo nel prodotto vettoriale: non stiamo più trattando gli scalari per i quali va sempre tutto bene…
Iniziamo inserendo il vettore v per primo (v Λ u). Cosa dice esattamente il simbolo Λ ? Diciamolo a parole:
Consideriamo il primo vettore come un qualcosa libero di ruotare attorno a una “vite” C. Prendiamo il secondo vettore (u) e trasliamolo fino alla punta di v (linea tratteggiata verde). A questo punto lasciamo che il vettore tratteggiato agisca come sa e come deve sul vettore “rotante” v. Il sosia verde di u non agisce tutto su v.
Per comprendere meglio la sua azione, scomponiamolo secondo due componenti vettoriali (sappiamo farlo benissimo, ricordate la somma dei vettori?): una lungo la direzione di v e una lungo la perpendicolare. Abbiamo i due vettori verdi. Quello diretto lungo CP vorrebbe fare qualcosa, ma non può! Il vettore v può ruotare ma non può allungarsi o restringersi. Insomma, questa componente è del tutto inutile. Ben diversa è la situazione per la componente perpendicolare. Lei è diretta verso l’alto del foglio e può trascinare il vettore v costringendolo a ruotare nel VERSO della freccia curva verde. E’ esattamente la stessa cosa che abbiamo già visto nel moto circolare uniforme. Il vettore componente perpendicolare di u tende ad andare per la sua strada, ma il vettore rigido v lo costringe a ruotare attorno alla vite C.
Non vogliamo certo fare della cinematica, ma tutto questo discorso ci è servito per capire cosa fa la vite C! Si sta avvitando o svitando? Beh… sta girando in senso antiorario e quindi la vite si svita. In altre parole, la vite si muove verso la direzione perpendicolare al foglio e verso di noi. Bene, questa è la direzione e il verso del vettore prodotto vettoriale.
Attenzione! Tutto ciò lo abbiamo ottenuto in quanto abbiamo considerato per primo il vettore v, ossia quello tenuto fermo dalla vite e in movimento rotatorio a causa del secondo vettore u. Più sinteticamente, abbiamo calcolato direzione e verso del vettore v Λ u. Questa scrittura possiamo perciò esprimerla come: il primo vettore v subisce l’azione “prodotto vettoriale” da parte del secondo vettore u; o -se preferite- il secondo vettore esegue l’operazione “prodotto vettoriale” su v.
Sì, lo ammetto, la mano destra sarebbe stata molto più semplice (e, infatti, la introdurremo tra poco), ma questa definizione un po’ contorta, ci permette già di vedere l’azione rotatoria di un vettore applicato a una certa distanza da un punto fisso. Il primo passo per il momento di una forza e per il nostro amico momento angolare.
Dato che siamo ostinati, continuiamo e spostiamoci nella Fig. 15b. Ormai sappiamo cosa dobbiamo fare. Il prodotto vettoriale è adesso u Λ v. No, non è la stessa cosa! Non siamo più tra i prodotti scalari o tra moduli, ma tra vettori veri e propri. Dobbiamo, quindi seguire l’ordine delle operazioni. Questa volta il vettore che è fissato alla vite diventa u, mentre è v quello che si sposta e si “scompone”. La componente perpendicolare (l’unica attiva) tende ad andare verso il basso del piano del foglio e a causare una rotazione oraria. In poche parole, la vite si avvita, ossia scende nella stessa direzione di prima, ma si allontana da noi.
I prodotti vettoriali ottenuti cambiando l’ordine dei due vettori ci indicano la stessa direzione, ma verso opposto. In poche parole, hanno segno opposto. Non vale quindi la proprietà commutativa, ma quella anticommutativa, ossia:
u Λ v = - v Λ u.
Per chiarire ancora meglio le idee, disegniamo la Fig. 16, in tre dimensioni, dove si vedono molto bene i due casi appena descritti.
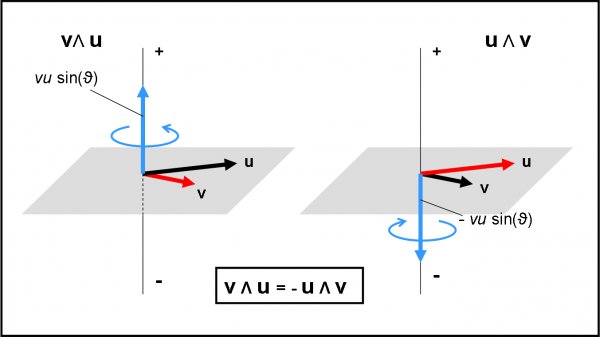
Voglio anche farvi notare un risvolto che ci sarà utilissimo… a tempo debito. Cambiando l’ordine, cambia il segno, ossia il verso, ma non il modulo (quello è sempre uguale). Riguardiamo le Fig. 15a e b. Il vettore v, che subisce a sinistra, è più corto di u, che subisce a destra. Tuttavia, a sinistra, il vettore verde che fa ruotare v (corto) è più lungo di quello che fa girare, a destra, il vettore u (lungo). In poche parole, su un vettore lungo agisce un vettore corto e viceversa. D’altra parte deve essere così dato che il modulo del vettore prodotto vettoriale deve rimanere uguale. Ridendo e scherzando abbiamo già “sfiorato” la conservazione del momento angolare…
Usiamo le dita della mano destra
A questo punto abbiamo capito molte cose e abbiamo anche messo il piede nel terreno della dinamica rotatoria, di cui il momento angolare è uno dei padroni indiscussi. Possiamo permetterci di introdurre la celeberrima regola della mano destra. Come si può fare per sapere immediatamente qual è la direzione e il verso di un prodotto vettoriale? Il dito indice della mano destra deve essere allineato con il primo vettore, il medio con il secondo vettore. Il pollice ci indica direzione e verso del vettore finale (nella Fig. 17, verso l’alto). Noterete facilmente che se invertiamo l’ordine dei due vettori il pollice imita quello degli imperatori romani negli spettacoli dei gladiatori: pollice verso, ossia verso il basso!
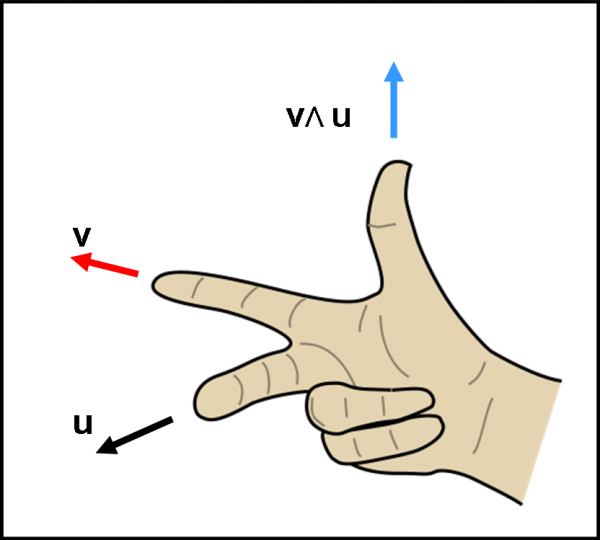
Ricapitoliamo il tutto, definendo compiutamente il vettore definito dal prodotto vettoriale:
Esso è, innanzitutto, un vettore che ha per modulo il prodotto dei moduli moltiplicati per il seno dell’angolo compreso (o -se preferite- ha come modulo l’area del parallelogramma che ha per lati i due vettori). La direzione è sempre perpendicolare al piano individuato dai due vettori. Il verso segue quello del pollice della mano destra.
Nella Fig. 16 i due vettori blu sono proprio i vettori risultanti, invertendo l’ordine dei due vettori nel prodotto vettoriale. La lunghezza dei vettori blu è, ovviamente, il modulo del prodotto vettoriale (uguale per entrambi).
Avanti i più curiosi …
Beh… è stato abbastanza faticoso. Chi vuole può fermarsi qui. Gli altri potrebbero però proseguire e mettere in azione i carissimi e simpaticissimi versori degli assi cartesiani x, y, z. E sì, ora devono comparire tutti e tre, per come è stato definito il prodotto vettoriale.
Noi conosciamo già i versori i e j, relativi agli assi x e y. Chiamiamo k quello relativo all’asse z, come si nota nella Fig. 18.
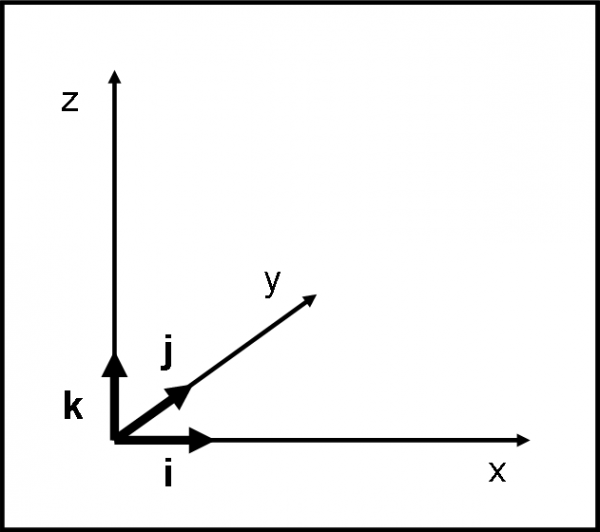
Prima di procedere, vi propongo un divertente esercizio. per verificare se avete digerito bene il prodotto vettoriale. Risolvete i seguenti prodotti vettoriali (eseguiti tra versori):
iΛ j =
jΛ k =
kΛ i =
j Λ i =
kΛ j =
iΛ k =
La soluzione la trovate nella Fig. 19 che segue (ma prima pensateci un po’…)
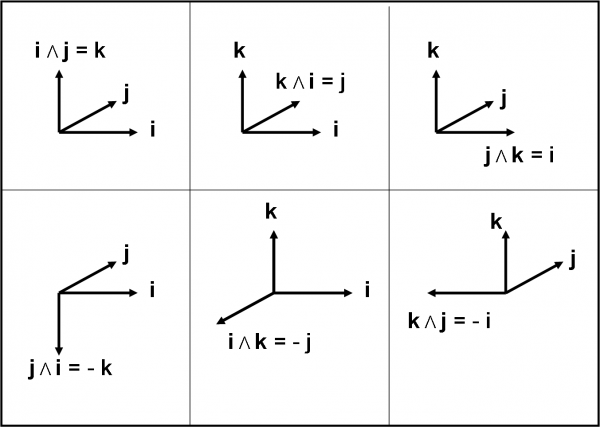
Dopo aver risolto l’esercizio, possiamo determinare le componenti lungo gli assi cartesiani (i moduli dei versori corrispondenti) del vettore prodotto di due vettori, in modo analogo a quanto fatto nell’articolo precedente. Consideriamo il caso più semplice, in cui i due vettori giacciono nel piano x,y.
v = vx i + vy j
u = ux i + uy j
e, quindi:
v Λ u = (vx i + vy j) Λ (ux i + uy j) = vx i Λ ux i + vy jΛ ux i + vx i Λ uy j + vy jΛ uy j
Ricordando che:
i Λ i = j Λ j = 0
si ha:
v Λ u = vy jΛ ux i + vx i Λ uy j
ma vale anche:
j Λ i =- k
i Λ j = k
per cui:
v Λ u =vx uy k -vy ux k = (vx uy - vy ux)k .... (13)
Come volevasi dimostrare: è un vettore che ha per modulo (vx uy - vy ux) e per direzione e verso quello del versore k, ossia dell’asse z.
Solo per gli … infaticabili
Complicandoci ancora un po’ la vita, si può considerare come piano dei due vettori v e u un piano qualsiasi e non proprio quello x,y. Ciò vuol dire che i due vettori hanno tre coordinate, una per ogni asse cartesiano (z compreso). Segue che:
v = vx i + vy j + vz k
u = ux i + uy j+ uz k
e con un po’ di lunghi, ma banali, passaggi matematici si ha, alla fine:
v Λ u =(vy uz - vz uy)i + (vz ux – vx uz)j + (vx uy - vy ux)k .... (14)
Provare per credere!
La soluzione di questa espressione completa del prodotto vettoriale si può compattare molto bene attraverso il determinante di un matrice quadrata tre per tre. In generale, le matrici sveltiscono enormemente molti calcoli di geometria analitica. Per gli incontentabili, scriverò un articoletto proprio sulle matrici in modo da permettergli di trovare velocemente la relazione (14) e poi anche la (13)...






3 commenti
Caro Enzo, innanzitutto volevo indicare alcuni piccoli refusi (o almeno penso).
Poco sotto la figura 14 si indica un inesistente segmento OH da moltiplicare per il modulo di u (presumo si tratti di PH).
Poco più sotto di indica VU = v sin (ϑ) (in realtà presumo si tratti di VH=v sin (ϑ) ).
Infine sotto la figura 15 si dice che il primo vettore è libero di ruotare intorno alla vite P (penso si tratti di C).
Volevo, però, descrivere un errore in cui sono incorso tentando di risolvere l'esercizio proposto e come ho cercato di inquadrare e risolvere il problema.
La questione riguarda il verso del vettore risultante.
Finché si è trattato di eseguire i prodotti di iΛ j e jΛ k tutto bene, il senso orario o antiorario è semplicissimo da individuare (io tendo ad identificare il secondo vettore, quello che esegue l'operazione prodotto sul primo, come quello che “trascina l'altro”, ma ognuno ha i suoi schemi mentali..).
Quando, però, si è trattato di eseguire i prodotti kΛ i e iΛ k , ho toppato completamente il verso del vettore risultante, come si vede nell'illustrazione seguente:
http://www.astrobin.com/full/78662/B/
Riflettendoci, l'errore era frutto di un approccio bidimensionale invece che tridimensionale.
A nulla son valsi inutili tentativi contorsionistici di applicare la regola della mano destra (che sarò strano, ma mi crea più confusione che chiarezza).
Per analizzare il problema, dapprima ho deciso di cambiare prospettiva alla figura tridimensionale, portando l'asse corrispondente al vettore risultante in posizione verticale.
http://www.astrobin.com/full/78662/C/
Visti da questa prospettiva, i prodotti kΛ i e iΛ k producevano un vettore risultante con verso corretto, ma la figura assumeva una diversa prospettiva.
Questo passaggio, però, mi ha permesso di trovare una soluzione capace di sgombrare il campo dagli equivoci in cui ero incorso, restituendomi una visione tridimensionale che mi consente di trovare con facilità il senso di rotazione e di conseguenza il verso del vettore risultante.
http://www.astrobin.com/full/78662/D/
Una volta risolto l'esercizio ho provato a calcolare il modulo del vettore risultante dal prodotto v Λ u, ottenendo la formuletta finale.
Questo è il procedimento seguito:
v=vx i + vy j + vz k
u=ux i + uy j+ uz k
v Λ u = (vx i + vy j + vz k) Λ (ux i+ uy j+ uz k)
v Λ u = (vx i ux i) +(vx i uy j) + (vx i uz k) + (vy j ux i) +( vy j uy j)+(vy j uz k) + ( vz k ux i) + ( vz k uy j) + ( vz k uz k)
Dato che:
i Λ i = j Λ j = K Λ K= 0
v Λ u = (vx i uy j) + (vx i uz k) + (vy j ux i) +(vy j uz k) + ( vz k ux i) + ( vz k uy j)
Inoltre, come trovato
iΛ j = k jΛ k = i kΛ i = j j Λ i =-k kΛ j =-i iΛ k =-j
per cui:
v Λ u = vx uy K - vx uz J - vy ux K + vy uz i + vz ux J - vz uy i
v Λ u = (vx uy - vy ux )K +( vz ux - vx uz)J +( vy uz - vz uy)i
In fin dei conti il titolo del tuo articolo già indicava l'importanza dell'avvitare o svitare.
Paolo
Ops, sul primo refuso, quello poco sotto la figura 14 il segmento OH in realtà dovrebbe essere VH (io ho erroneamente scritto PH).
Paolo
caro Paolo,
innanzitutto, grazie per i refusi... volendo scrivere direttamente in word (senza passare dal foglio) è molto più facile sbagliare soprattutto per uno che comincia a rimbambire del tutto... Meno male che ho assistenti bravissimi come te!!!!
Nessun problema per la mano destra... come hai visto anch'io l'ho abbastanza trascurata, ma tanti la usano normalmente e quindi non potevo non metterla. Hai visto che la figura di copertina indica proprio cosa può capitare...
Ognuno usi pure il sistema che preferisce, l'importante è riuscire a visualizzare la tridimensionalità. Il tuo sistema va benissimo e anch'io di solito avvito e svito...
OK per gli esercizi. Il prossimo articoletto ti verrà proprio a fagiolo...