Categorie: Fisica classica
Tags: forza centrifuga forza di Coriolis forze fittizie prodotto vettoriale sistemi inerziali sistemi NON inerziali
Scritto da: Vincenzo Zappalà
Commenti:1
Gira, il mondo gira: la Forza di Coriolis. 5: (tiriamo le somme)**
Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.
Tiriamo un po’ le somme, dopo i tanti esempi che abbiamo illustrato, per mettere in evidenza la forza di Coriolis e la sua cara sorella centrifuga. Va bene la semplicità grafica, ma un po’ di fisica non guasta mai. In particolare, dobbiamo capire bene quanto e come siano attive, in un vero gioco di squadra! Reputo, perciò, questo semplice articolo molto utile per legare insieme tutto quanto detto finora… non saltatelo!
E’ vero, abbiamo scherzato molto, tra un quiz e l’altro, con le traiettorie viste da un sistema inerziale e da un sistema rotante. E tutto ciò è servito solo e soltanto per potere applicare sempre e comunque le leggi della dinamica newtoniana. Non pensiamo, però di avere solo giocato… Le varie traiettorie ci dimostrano molto bene come le due accelerazioni fittizie (chiamiamole pure così) riescano perfettamente nel loro compito. Lavorando geometricamente le abbiamo trovate quasi automaticamente, ma sappiamo molto bene che esse si calcolano abbastanza facilmente anche attraverso un paio di derivate o poco più (QUI). Cerchiamo di collegare con molta semplicità le due visioni, sapendo molto bene che il risultato deve essere sempre lo stesso.
La collaborazione tra l’accelerazione di Coriolis e di quella centrifuga è decisamente molto fruttuosa. Ricordiamo, innanzitutto, che esse esistono solo nei sistemi non inerziali ed è proprio per questo che vengono chiamate “fittizie”. La centrifuga agisce quando cambia la distanza radiale (o per non farla cambiare, come nel moto circolare uniforme), mentre quella di Coriolis dipende essenzialmente dalla velocità con cui si muove l’oggetto. A volte predomina l’una, a volte l’altra, ma non possono fare a meno di lavorare in grande armonia e riuscire a riprodurre esattamente ciò che capita nel sistema inerziale.
Ricordiamoci della pallina tenuta in rotazione da una corda. Se la corda funziona, la pallina risulta ferma nel sistema rotante e l’unica accelerazione che si deve creare per questo scopo è quella centrifuga. Nel sistema inerziale basta invece quella centripeta (reale). A un certo momento, tagliamo la corda: per un sistema inerziale tutto è ovvio e facile: abbiamo di fronte una traiettoria rettilinea che conferma pienamente il principio d’inerzia. Come viene a mancare l’unica forza agente sulla pallina (quella centripeta), la pallina riprende il suo moto rettilineo e uniforme. Tutti i sistemi inerziali vedrebbero la stessa cosa.
Un sistema rotante, che vuole considerarsi fermo, deve accettare la stessa conclusione, ma per lui è molto più difficile darne una spiegazione. La sua stessa rotazione impone un movimento rotatorio alla pallina (quello che capita a lui, lo trasferisce alla pallina). Sì, andrebbe anche bene, ma il fatto è che per le leggi di Newton una traiettoria curva deve subire almeno un’accelerazione.
Ma una non basta, dato che mentre il sistema ruota, e vede la pallina viaggiare per la sua traiettoria, cambia continuamente anche la sua distanza dal centro di rotazione e ciò implica l’accelerazione che ben conosciamo, quella centrifuga.
Spostandoci su una piattaforma rotante e facendo muovere la pallina (senza attrito e senza forza di gravità) dal centro verso l’esterno, un modo estremamente indicativo per dimostrare la corrispondenza tra sistema inerziale e non inerziale è proprio l’angolo α, quello che indica dove l’oggetto esce dalla piattaforma. Esso deve restare lo stesso per entrambi i sistemi, dato che il fenomeno meccanico deve restare uguale.
Consideriamo proprio questa situazione, che è la più semplice e dove è più facile notare ciò che realmente succede, istante per istante. La configurazione è allora quella, ormai ben nota, della pallina che viene lanciata, con velocità costante e senza attrito, a partire dal centro di rotazione.
Guardando come evolve il movimento apparente, si possono capire i contributi delle due accelerazioni (o delle forze se introducessimo anche la massa della pallina).
Nel sistema inerziale (Fig. 1) tutto è di una semplicità quasi ridicola: la pallina si muove, ad esempio, di un metro al secondo mentre descrive la sua traiettoria verso l’alto, obbedendo alla legge di Newton.
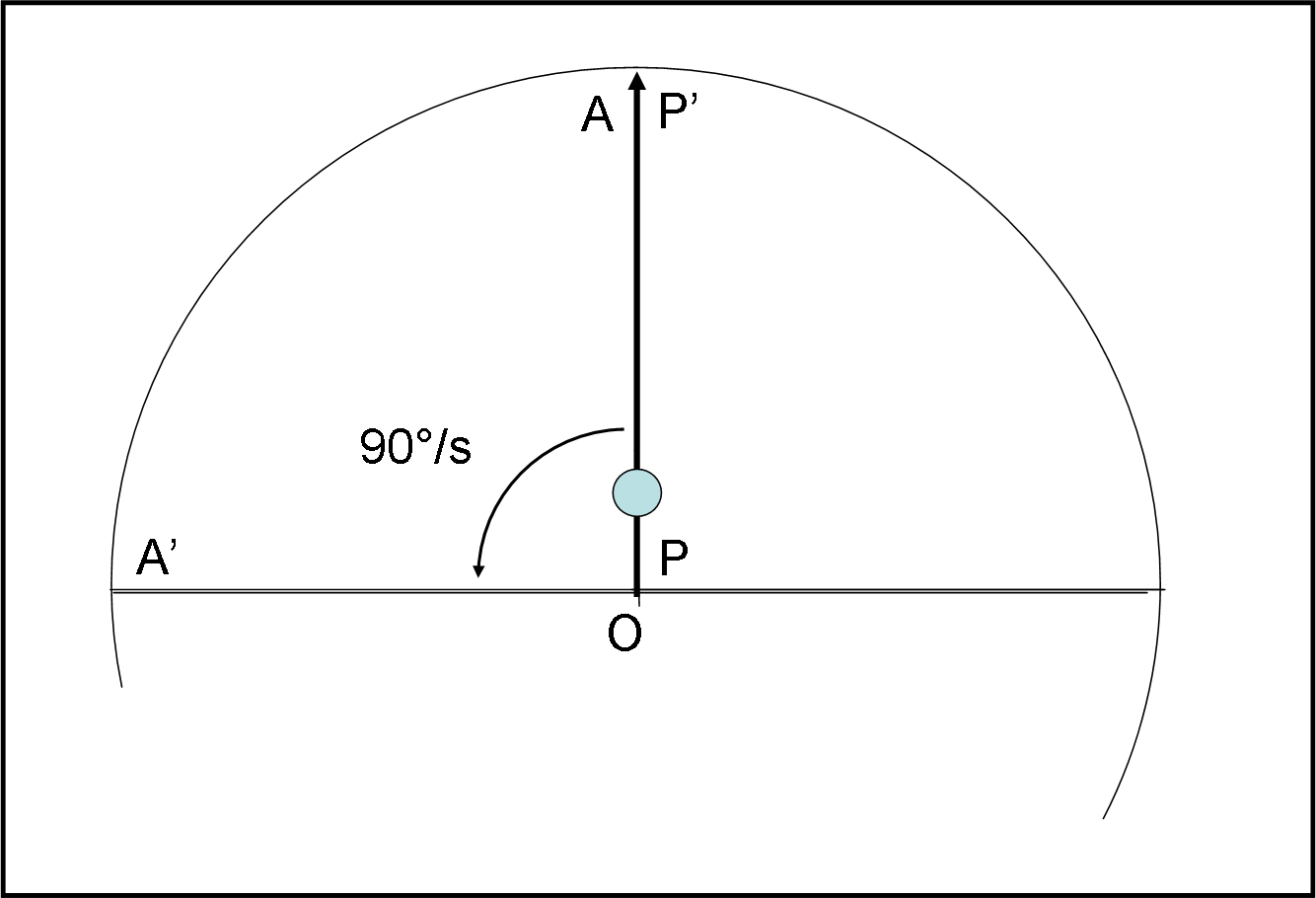
Se nessuna forza la viene a disturbare, lei continua in quel moto per l’eternità. Tuttavia, notiamo subito un risultato abbastanza sconcertante. La pallina, nel suo moto rettilineo, non può certo vietare alla piattaforma rotante di fare il suo mestiere (ad esempio ruotare di 90° al secondo). Quando arriva al bordo, il punto A che, al momento del lancio, si trovava proprio lungo la linea verticale del movimento della pallina, si è ormai spostato verso sinistra in A’. Tra la pallina P’, al momento dell’arrivo sul bordo, e il punto A’ si determina l’angolo α, dipendente sia dalla velocità della pallina sia dalla velocità di rotazione della piattaforma. Questo angolo α deve rimanere lo stesso anche quando l’osservatore si trova nel sistema rotante.
Spostiamoci, allora su di lui. Ciò vuol dire, essenzialmente, che il punto A si considera fermo e quindi coincide sempre con A’. Come conseguenza deve essere la pallina a subire un cambiamento di percorso per potere uscire in P’, alla stessa distanza angolare α, misurata precedentemente (Fig. 2)
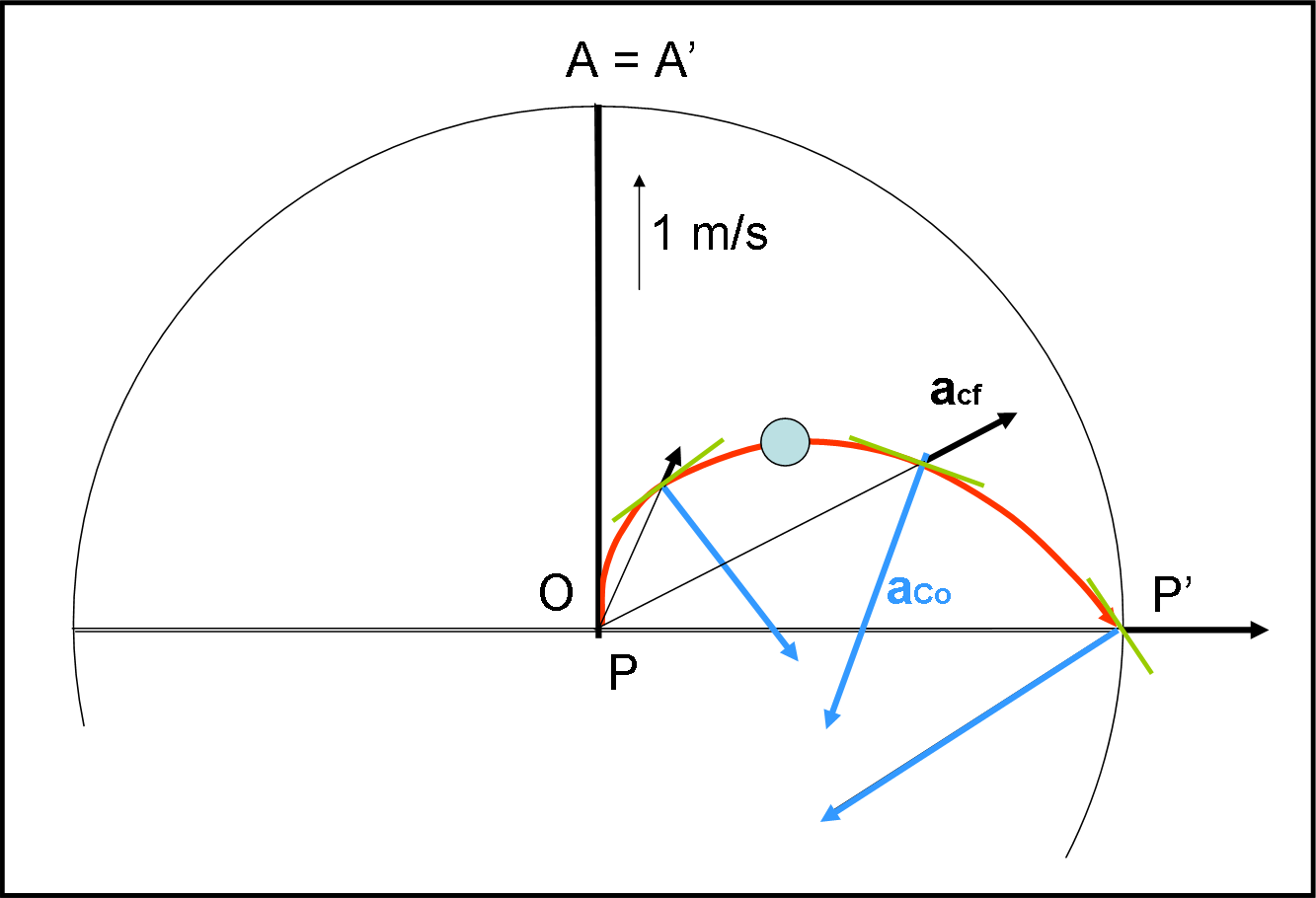
Le cose diventano più complicate. La pallina è costretta a descrivere un curva per poter confermare il fenomeno meccanico. Come già detto, ciò implica, secondo le leggi di Newton, che debbano intervenire ben due forze “fittizie” per ottenere il risultato cercato, ossia per confermare che nel sistema inerziale il movimento sia rettilineo e uniforme e che la pallina esca da P’. Un fatica non da poco, solo e soltanto per dare soddisfazione a quel genio di Newton…
Non è difficile disegnare la velocità nel sistema rotante, quella che ci ha permesso finora (utilizzando metodi grafici apparentemente diversi) di tracciare la traiettoria della pallina vista dal sistema non inerziale. In realtà, non abbiamo fatto altro che sommare la velocità costante e rettilinea del sistema inerziale a quella perpendicolare alla distanza della pallina dal centro (r’), che altro non è che la formuletta ricavata QUI.
v’ = v – ω ∧ r’
v è proprio la velocità nel sistema inerziale, mentre il prodotto vettoriale regala quella perpendicolare alla congiungente il centro O con la pallina. Usate la mano destra, puntando l'indice (ω) verso l’alto, il medio in direzione di r’ e troverete che il pollice vi indica la direzione della velocità ω ∧ r’. Basta cambiare il segno e direzione e verso sono ricavati. Il modulo (visto che si lavora con angoli retti) vale proprio
v’ = v – ωr’
In tal modo (o graficamente come abbiamo fatto noi) posiamo determinare la traiettoria punto per punto o, ancora meglio, conoscendo la traiettoria della curva, determinare la tangente punto per punto. Conoscere la tangente, vuole dire conoscere la velocità (il modulo lo sappiamo) v’ nel sistema rotante. Siamo pronti, a questo punto, a disegnare le accelerazioni che agiscono in qualsiasi punto in cui si trovi la pallina.
Dalla poca matematica sviluppata QUI, sappiamo quanto valgono le accelerazioni centrifuga e di Coriolis.
La prima vale:
aCF = - ω ∧ (ω ∧ r’)
Proviamo a girare due volte la mano destra e troviamo che questa accelerazione va sempre in verso radiale (ossia da O verso P). Essa, nel nostro caso semplificato, non ha bisogno di funzioni trigonometriche, è ha come modulo:
aCF = - ω2r’
Passiamo a quella di Coriolis, che ha come valore:
aCo = - 2(ω ∧ v’)
Conoscendo ormai v’ e avendo la mano destra ben allenata, si trova subito che essa è diretta in direzione perpendicolare alla tangente (velocità) istantanea.
Bene, disegniamo il tutto nella Fig. 2. ricordando che abbiamo imposto una velocità di partenza uguale a un metro al secondo e una velocità angolare di 90° gradi al secondo. Non ci vergogniamo certo di ragionare in modo quasi fanciullesco. Si vede bene come l’accelerazione di Coriolis tenda a spostare verso destra la traiettoria, mentre quella centrifuga tenda ad allungarla verso l’esterno. In parole molto semplici, vi è un continuo cambiamento della distanza r’, che comporta un’accelerazione centrifuga, e una continua variazione della direzione di v’ che comporta l’accelerazione di Coriolis. Entrambe dipendenti dalla rotazione del sistema non inerziale. Ripeto ancora: tutta questa fatica viene compiuta per far sì che il punto di uscita dalla piattaforma rotante coincida con quello trovato nel sistema inerziale.
In modo analogo, potremmo calcolare le accelerazioni, partendo dal bordo esterno e andando verso il centro, ricordando, però, che la traiettoria inerziale della pallina è sempre una retta, ma inclinata…
Una riflessione finale molto personale: non trattiamo male i sistemi non inerziali. Sembrano complicati, ma pensiamo alle strategie che devono usare per soddisfare i loro più fortunati amici inerziali. Inoltre, ricordiamo che solo i sistemi non inerziali sono capaci di piegare perfino la luce! E dico poco…
In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis






1 commento
Come diceva Dario Fò nel suo Mistero Buffo: "Attento a te!!!".
Chi non legge questo articolo non mi venga poi a chiedere perché gli uragani ruotano come girandole o perché l'acqua del lavandino scappa sempre dalle mani...