Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

 

Bene, molto bene. Molti hanno risposto e praticamente tutti hanno svolto il quiz correttamente. Tuttavia, data la grande importanza che riveste questo argomento e la tanta confusione che viene spesso fatta in giro per la rete, è meglio ripetere le operazioni da svolgere passo dopo passo in modo da capire non solo la parte “pratica”, ma l’essenza fisica di ciò che andiamo a costruire. Un discorso che deve essere capito da tutti, dato che è veramente un’avventura da seguire con attenzione e senza vere difficoltà. Le considerazioni finali, poi, innescano un nuovo piccolo quiz… Mi raccomando: non snobbate questo articolo, perché è profondamente esplicativo per tutti e ci permette di conoscere sempre meglio le forze fittizie: un argomento veramente fondamentale!

Cominciamo col ripetere le condizioni di partenza, continuando a segnare in nero il sistema fermo e in rosso quello rotante. La palla è tenuta dalla corda e ruota attorno all’origine O = O’ con velocità angolare ω. Palla e corda sono disegnate in rosso, dato che appartengono (ossia sono solidali) con il sistema rotante. Come ben sappiamo il tutto capita per merito di una sola forza reale (ossia esistente nel sistema inerziale): la forza centripeta, rappresentata dalla corda che non fa scappare la palla e le permette di mantenere la sua velocità costante (in modulo). Così pensa l’osservatore solidale con il sistema fermo: lui vede corda e palla ruotare con grande regolarità (Fig. 1).

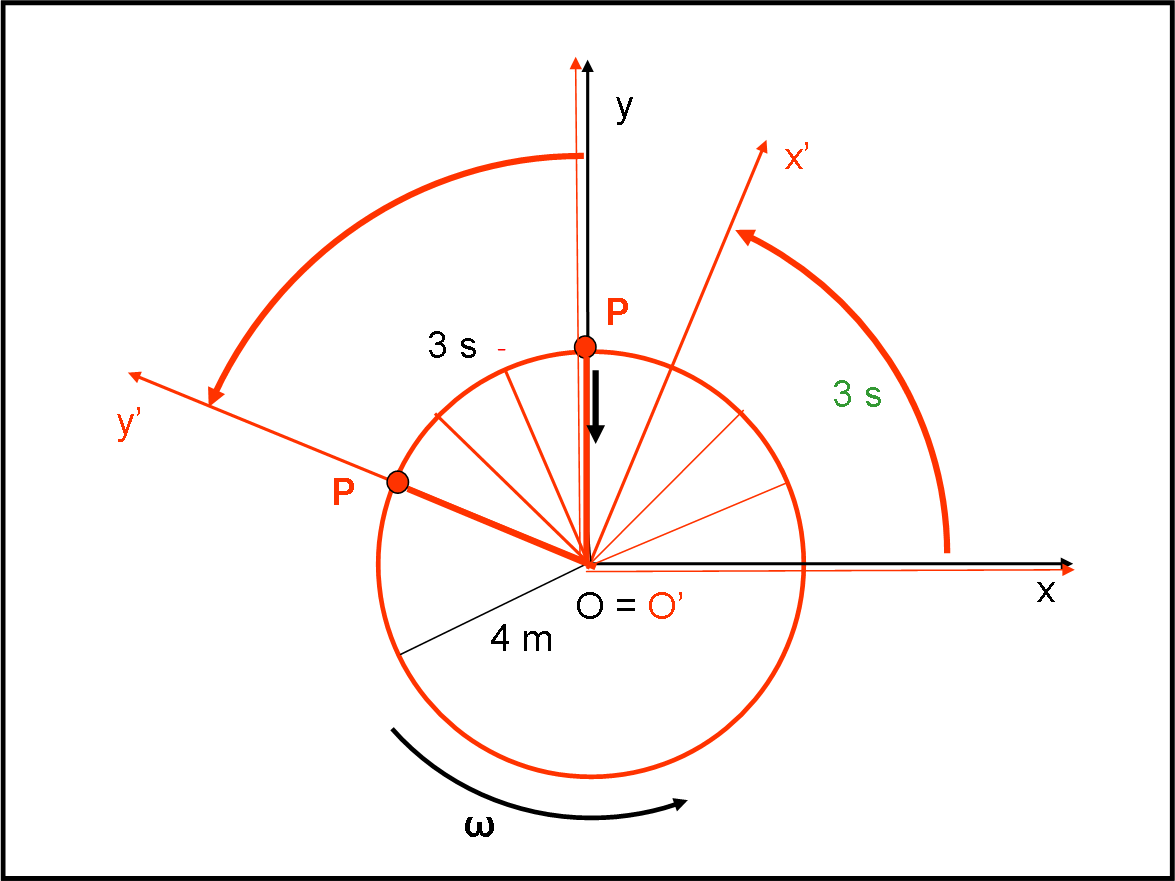
Ben diversa è la situazione per l’osservatore solidale con il sistema rotante. Per lui la palla e la corda sono sempre ferme (Fig. 2).

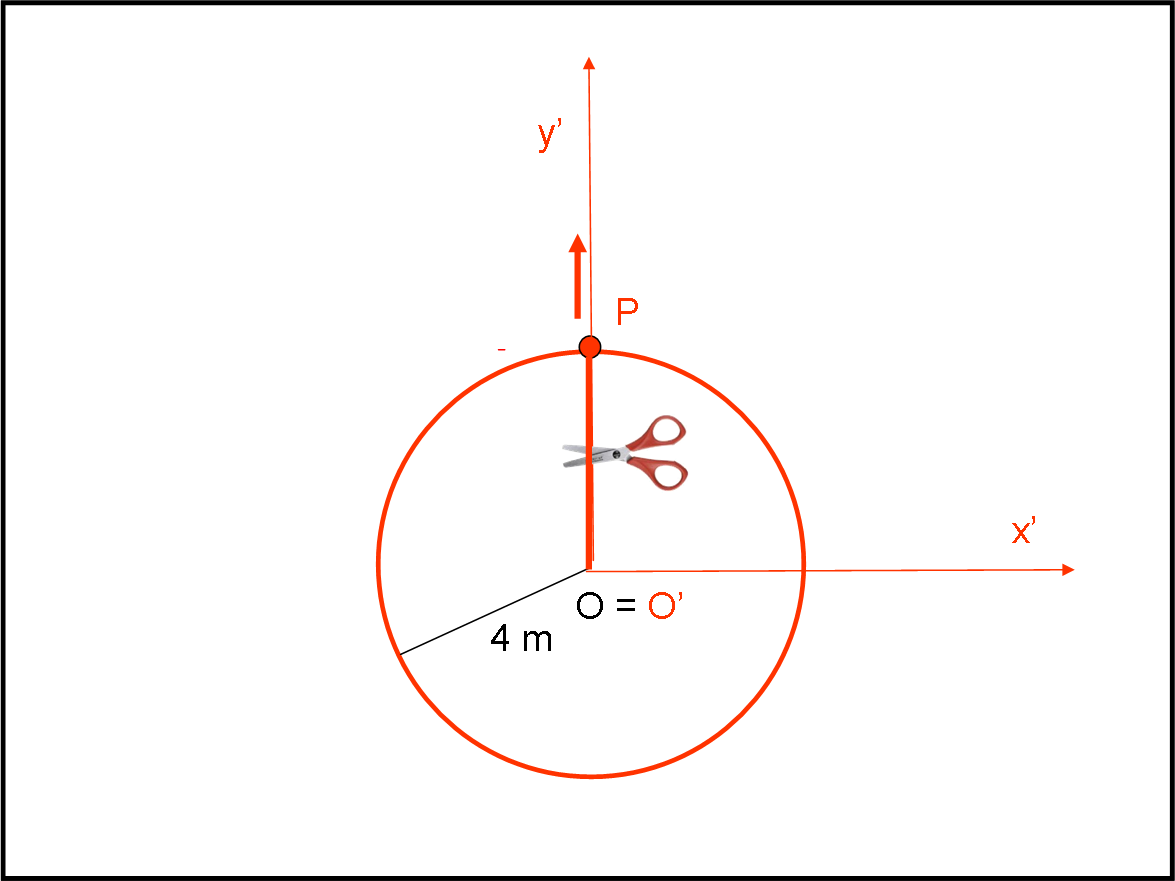
Se si mettesse sopra la palla sentirebbe una forza che sembrerebbe trascinarlo verso l’esterno in senso radiale (forza centrifuga), ma la corda riesce a non farlo scappare in quella direzione. Un gioco di tira e molla che si svolge in posizione statica, senza avvertire nessuna rotazione. Caso mai è tutto lo stadio esterno che sembra ruotare con velocità angolare - ω, ossia in senso orario. Ma non pensiamo a questo e torniamo alla nostra pedana. E’ giunto il momento di tagliare la corda!

L’osservatore solidale con il sistema rotante è pronto a scommettere che la palla se ne vada in senso radiale, seguendo quella forza che la spingeva verso l’esterno. Subito dopo il taglio, l’impressione è proprio quella, ma poi…

Per comprendere meglio cosa succede, portiamoci nel sistema fermo e guardiamo le cose da un sistema inerziale, dove le leggi di Newton si applicano senza problemi. Tagliando la corda, viene a mancare l’unica forza che tratteneva la palla e la costringeva a ruotare (forza centripeta). La palla non può che seguire la legge di Newton e andarsene lungo la direzione tangente alla circonferenza, nella direzione della velocità istantanea (Fig. 3).

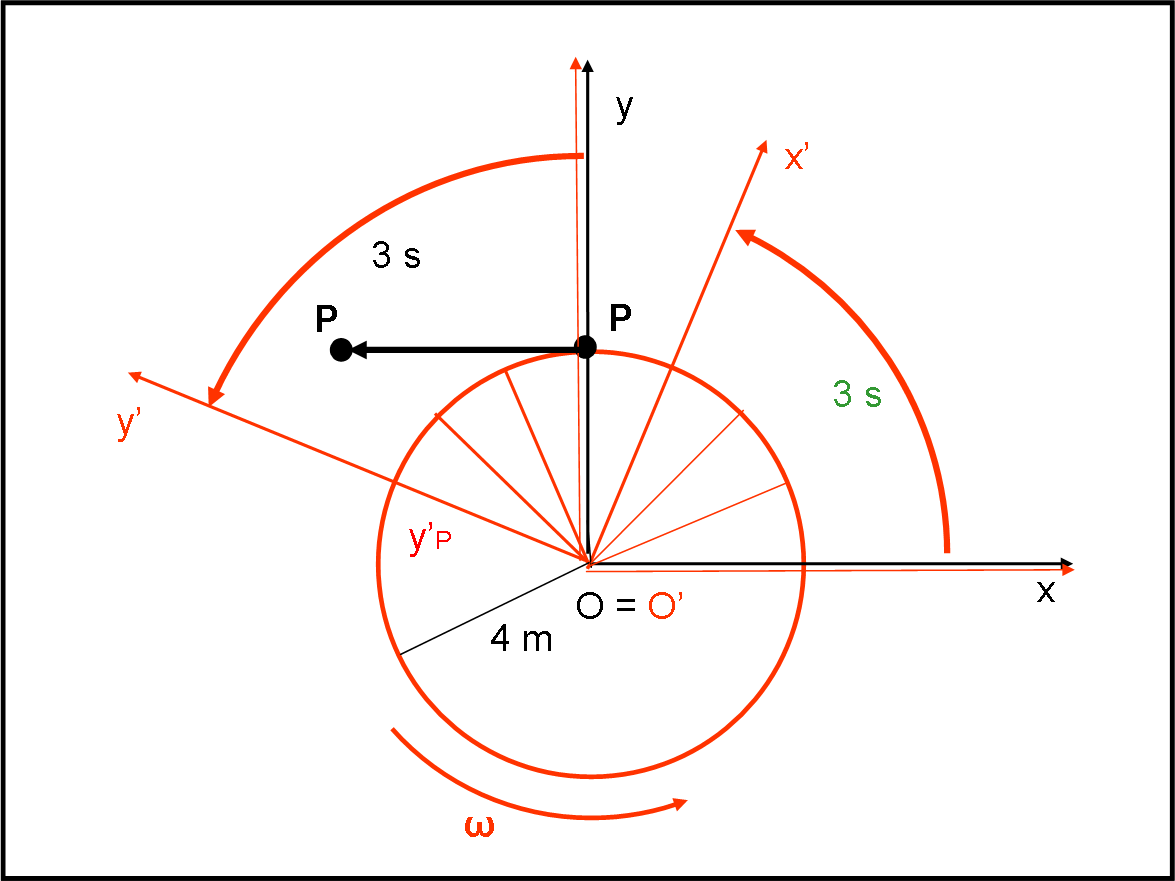
Attenzione: questa velocità si mantiene e rimane costante, dato che non esistono più forze a darle fastidio. A questo punto la palla P diventa nera dato che appartiene al sistema inerziale dello stadio. Il suo moto è rettilineo e uniforme.

Torniamo al sistema rotante. Come vede la traiettoria della palla P? Facile a costruirsi. Facciamo ruotare gli assi rossi di un certo angolo (freccia curva rossa) e vediamo quali sono le coordinate x’ e y’ della palla P rispetto agli assi rotanti rossi. Basta tracciare le perpendicolari agli assi x’ e y’. Queste coordinate le abbiamo disegnate in verde (Fig. 4).

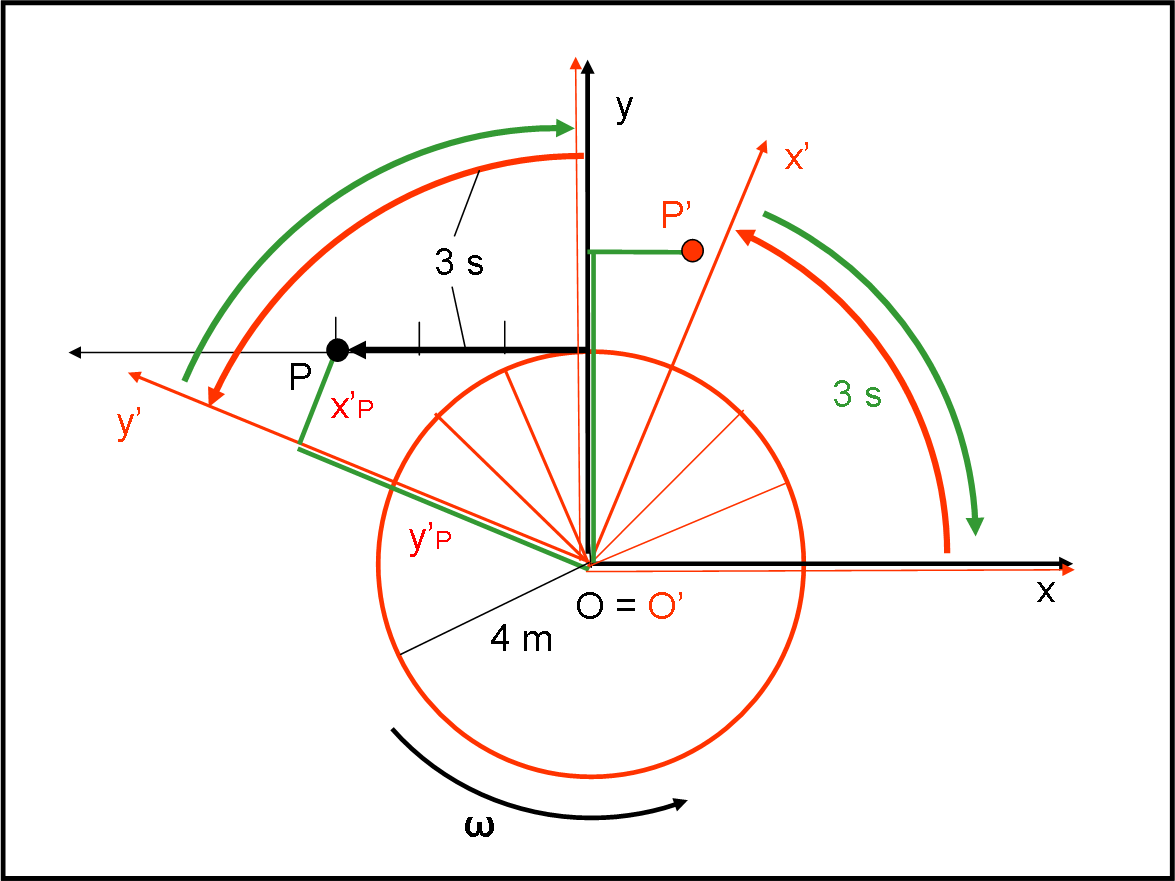
Il sistema, però, si considera fermo e, perciò, conviene riportare l’asse y’ nella posizione iniziale, utilizzando la rotazione inversa disegnata in verde. Troveremo il punto P’, che indica la posizione della palla P nel sistema rotante (possiamo disegnarla in rosso).

Per disegnare tutta la traiettoria, bisogna calcolare di quanto si sposta la palla P lungo la traiettoria rettilinea (verso sinistra), in un secondo. Nello stesso tempo, gli assi rossi ruotano di un certo angolo.

Sappiamo che il periodo T è di 16 secondi, così come sappiamo che il raggio R (lunghezza della corda) è di 4 metri.

Abbiamo subito il valore della velocità angolare:

ω = 2π/T = 6.28/16 rad/s

La velocità tangenziale, ossia la velocità costante della palla (moto circolare uniforme) è data da:

v = ω R =  (6.28·4)/16 = 6.28/4 = 1.57 m/s

Spostando la palla del valore di 1,57 m sulla linea orizzontale verso sinistra, si devono ruotare gli assi rossi di 22.5°, proprio l’angolo descritto in un secondo dal sistema rotante: 360/16 = 22.5°.

Ottenuto il primo punto P’, si ruota il sistema rosso di un altro angolo di 22.5°, portandolo a 45° rispetto alle condizioni iniziali (y’ = y). Si trovano le nuove coordinate e si ripete l’operazione eseguita in Fig. 4. E via dicendo, stando bene attenti alle coordinate del nuovo punto P rispetto agli assi rossi ruotati dell’angolo corrispondente. Alla fine si ottiene, in un periodo di tempo di 8 secondi (mezzo periodo) la curva di Fig. 5.

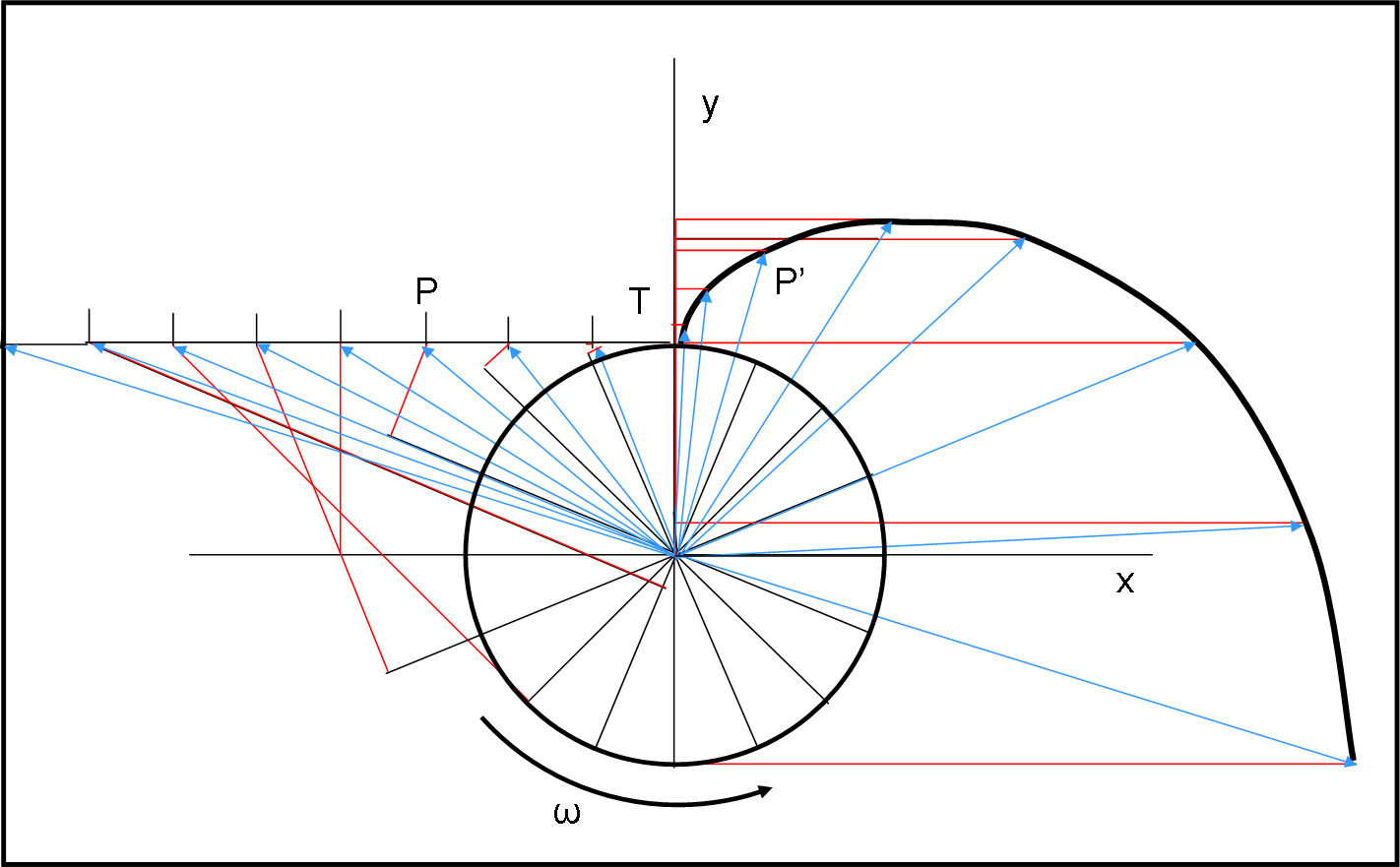
Mamma mia! Altro che scappare lungo la direzione della forza centrifuga… otteniamo una curva che si allarga sempre di più verso destra. Una spirale, ma c’interessa poco il suo nome matematico, dato che vogliamo soprattutto capire come questa strana situazione possa capitare. Se abbiamo letto attentamente questo articolo non è difficile comprenderlo, ma lo faremo lavorando insieme.

Innanzitutto ci deve essere una qualche forza “aggiuntiva” che tende a far curvare la traiettoria, rispetto a quella rettilinea che sembrava essere indicata dalla forza centrifuga. Due forze che agiscono insieme e che non esistono nel sistema inerziale.

Cerchiamo di capire la faccenda in modo molto qualitativo, per adesso…

Consideriamo le frecce azzurre. Per ogni posizione P della palla esse indicano di quanto si è spostata la palla in senso radiale. In altre parole, illustrano come sembra muoversi a causa della sola forza centrifuga. Fosse stata da sola, questa forza avrebbe fatto spostare, come immaginato in un primo momento, la palla P lungo l’asse verticale (l’asse y’ iniziale, considerato fermo). E invece, vi è un netto e chiaro spostamento verso destra… spostamento curvilineo, come già detto. Niente da fare, abbiamo di fronte una nuova forza! Questa forza è proprio la forza di Coriolis e nasce quando si ha un sistema rotante e un punto P che si muove con una certa velocità. Proprio il nostro caso: noi abbiamo la rotazione, ma anche lo spostamento di P lungo la retta TP.

Tenendo sempre presente i semplici calcoli eseguiti QUI, si può facilmente ottenere la velocità istantanea della palla P’ lungo la strana traiettoria e anche le forze che agiscono su di lei. Ci arriveremo…

La forza di Coriolis, la famosa forza di Coriolis, che sulla nostra Terra tutto fa meno che far girare l’acqua nei rubinetti (o nei bicchieri di vino...). Attenzione, però, a non confondersi. Nel caso trattato finora, ciò che vedrebbe un alieno dal di fuori (sistema inerziale), sarebbe una velocità rettilinea e uniforme della palla. D'altra parte, notando la bella curva ottenuta, sembrerebbe ovvio passare alle curve spiraleggianti dei cicloni e anticicloni terrestri. Ma ne siamo proprio sicuri? No, assolutamente no. Potremmo dire, frettolosamente, che i cicloni nascono direttamente dalla forza di Coriolis e che quindi sono visibili nel sistema terrestre. Fosse questa la verità, come mai, allora, i cicloni sono visti anche da un alieno, che dovrebbe vedere delle rette e non delle curve? Coriolis ci vuole, ma non solo...

Beh… cercheremo di spiegarlo al meglio, ma intanto cominciate a pensarci… e -se volete- rispondete pure. In fondo, è un nuovo piccolo quiz…

 

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis