Questo articolo è inserito nella sezione d'archivio dedicata all'Elettromagnetismo

Descriviamo i due teoremi fondamentali (della divergenza e del rotore) che ci permetteranno di passare dalle equazioni di Maxwell in forma integrale a quelle in forma differenziale.

Premessa

Ogni punto dello spazio è soggetto a due campi "separati", quello elettrico e quello magnetico, che possono essere sintetizzati con due vettori. Essi possono essere diretti in qualsiasi direzione rispetto al moto della carica (ad esempio, una carica che viaggia sotto l'azione del campo elettrico può essere deviata dal campo magnetico). Non stupiamoci, quindi, se d'ora in poi le derivate saranno sempre considerate parziali. Resta sempre la condizione che prodotti scalari tra vettori perpendicolari tra loro danno come risultato zero e lo stesso capita per prodotti vettoriali tra vettori che sono paralleli tra loro.

La forma integrale è stata utile per descrivere i campi e le loro relazioni su zone di spazio delimitate da superfici di qualsiasi estensione, la versione differenziale è, invece, utile per descrivere cosa capita punto per punto nello spazio. L'utilizzo degli integrali è fondamentale, trattandosi di superfici comunque estese che quindi necessitano di somme di tante superfici estremamente piccole, mentre si tratta con differenziali, quando si vuole descrivere ciò che capita nell'intorno infinitesimo di un certo punto. Una cosa è il calcolo, ad esempio, del flusso entrante o uscente da una qualsiasi superficie; un'altra è studiare il contributo di un singolo punto dello spazio.

Per passare da una forma all'altra è necessario applicare due teoremi fondamentali, che prendono il nome di teorema della divergenza e teorema del rotore. Iniziamo ad analizzare il primo e a usarlo per cambiare veste alle prime due equazioni di Maxwell.

Teorema della divergenza

∫div(F) dV = ∫F x dA                      .... (2)

Senza spaventarci prima di averlo affrontato accuratamente possiamo notare come esso uguagli due integrali, uno esteso a un volume (notiamo il dV) e l'altro a una superficie (notiamo il dA).

Cominciamo con la parte destra della relazione (2)

Come significa l'area A? Non è altro che la superficie che racchiude un certo volume V. Ne segue che A e V sono strettamente legati tra loro. Ovviamente, la superficie può delimitare qualsiasi forma si voglia. Noi ne consideriamo una regolare, ma la faccenda può essere tranquillamente estesa a qualsiasi superficie. L'unica cosa veramente importante è che essa deve essere una superficie CHIUSA. F rappresenta un campo vettoriale, che, nel nostro caso può essere sia quello elettrico E che quello magnetico B. F (e quindi sia E che B) ha tre componenti rispetto agli assi cartesiani (F_x, F_y, F_z o, se preferite, F_x i, F_y j, F_z k).

Consideriamo un cubo di superficie esterna A e di volume V. dA è una piccolissima parte della superficie A e possiamo indicarla con un quadratino (Fig. 17). Come ormai abbiamo imparato dai capitoli precedenti, dA è anch'esso un vettore, di modulo dA e diretto ortogonalmente al quadratino, con verso uscente.

Sappiamo, allora, molto bene cosa significa il prodotto scalare che compare nell'integrale: il prodotto scalare tra il campo vettoriale e il vettore dA. Richiamiamo il valore SCALARE di questo prodotto che è dato dalla somma dei prodotti scalari delle tre componenti del vettore campo per il vettore dA.

F x dA = Fx x dA_x + Fy x dA_y + Fz x dA_z

Per come è definito il prodotto scalare, esso, per ogni piccola area dA, è dato dal prodotto tra  la componente di F_n di F ortogonale all'area, ossia parallelo al vettore dA, e lo stesso vettore dA (Ovviamente, ogni componente di F, rispetto agli assi cartesiani di riferimento, darà un suo contributo a questa componente "normale").  La componente Fp, ortogonale al vettore area dA, dà un contributo nullo al prodotto scalare.

La Fig. 18, ci mostra allora cosa rappresenta l'integrale: la somma di tutti i prodotti scalari tra le componenti del vettore F ortogonali alla superficie e i loro corrispondenti vettori dA.

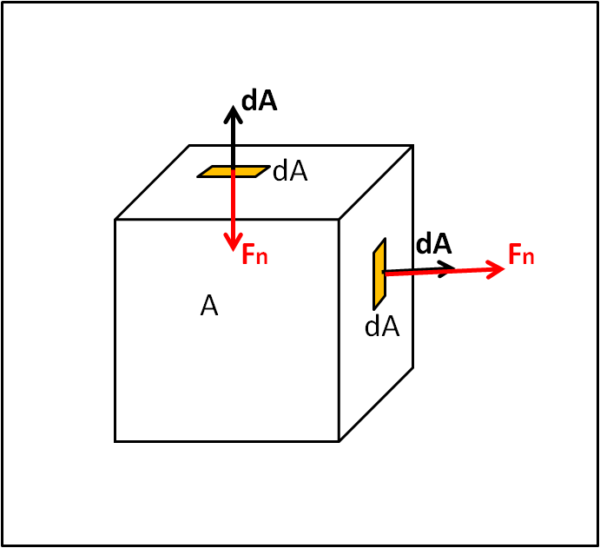
Essi possono avere valori numerici molto diversi tra loro, dato che F può avere modulo, direzione e verso diversi in ogni singola area dA. Infatti, F può sia entrare che uscire dalle piccole superfici e può essere più meno "intenso", ma l'importante è che venga considerata solo la sua componente perpendicolare alla piccola area dA.

In poche parole, per riportarci con i piedi per terra, abbiamo solo definito nuovamente il campo che entra o esce o dall'intera superficie.  Abbiamo parlato tanto, ma abbiamo ripetuto qualcosa che già conosciamo molto bene. L'integrale di destra non è altro che il flusso Φ del campo vettoriale (ripetere certe cose può aiutare a comprenderle sempre meglio).

Ne segue che il nostro integrale di destra può rappresentare perfettamente  sia il flusso del campo magnetico Φ_B che di quello elettrico Φ_E.

Occupiamoci, adesso, dell'integrale a sinistra della relazione (2). In questo caso dobbiamo avere a che fare con tutti i volumetti dV interni alla superficie A, che sommati danno proprio il volume totale V.

∫div(F) dV

Ma noi sappiamo perfettamente bene cosa significa  applicare l'operatore div a un vettore in un volumetto dV (ricordiamoci il primo capitolo). Vuol dire nuovamente eseguire un prodotto scalare tra le varie componenti e i vettori  relativi alle singole facce del volumetto. L'integrale di sinistra ci dice solo di sommare tutti contributi della divergenza dei volumetti che compongono il volume V. Tuttavia, non è difficile intuire che ciò che per un volumetto è un vettore di campo entrante diventa anche un vettore di campo uscente per il volumetto adiacente. In poche parole tutti i contributi della facce dei volumetti interni si annullano tra di loro. Che cosa rimane alla fine? Solo e soltanto il contributo delle divergenze sulle facce esterne dei volumetti. Siamo, perciò, nuovamente di fronte a una somma dei flusso uscenti dalla ed entranti nella superficie esterna.

Risulta perciò veramente ovvio il segno di UGUALE della relazione (2). I due integrali, uno relativo al volume e uno relativo alla superficie sono esattamente la stessa cosa!

Se vi sembra che abbia detto delle banalità, sono molto contento: vuol dire che siamo arrivati a questo punto capendo perfettamente bene il significato di divergenza e di prodotto scalare.

Ribadiamo il tutto con la Fig. 19.

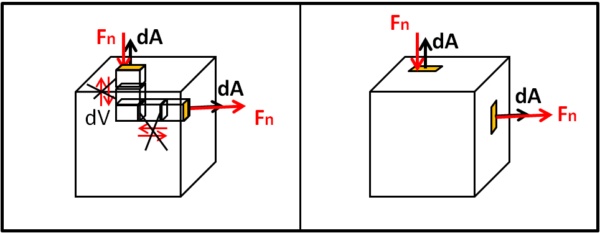
La parte sinistra (divergenza del campo dei vari volumetti) e la parte destra (prodotti scalari tra campo e  superficie esterna) sono esattamente uguali, dato che i contributi delle superfici dei volumetti interni si elidono tra di loro e restano solo i contributi delle facce esterne. Non banalizziamo troppo la faccenda. Il teorema è fondamentale in quanto uguaglia due integrali, uno esteso a un volume e uno esteso a una superficie

Teorema del rotore

La faccenda è solo apparentemente più complicata, ma, nuovamente, se abbiamo compreso bene il significato di rotore, il tutto diventa banale. Anzi, si semplifica addirittura, dato che abbiamo a che fare con integrali di linea e di superficie. Il salto in più è legato al fatto che fanno la loro comparsa le derivate rispetto al tempo del nostro campo vettoriale.

∫rot(F) x dA = ∫F x dl

Abbiamo di fronte due integrali formati da prodotti scalari: il primo tra il vettore rotore del campo e il vettore area;  il secondo tra il vettore campo e il vettore "segmentino" (un integrale, quest'ultimo, che descrive una circuitazione lungo un "filo").

Guardiamo la parte destra. Ci troviamo su una linea che si chiude su stessa, ad esempio, il perimetro di un quadrato, e immaginiamo che  il movimento avvenga in senso antiorario. E' molto semplice intuire che stiamo effettuando un prodotto scalare tra il vettore del campo F e un vettore infinitesimo dl che indica, punto per punto, la direzione e il verso della circolazione. Trattandosi di un prodotto scalare tutto ciò che rimane del campo è solo la componente parallela al vettore dl (la componente perpendicolare dà un contributo nullo al prodotto scalare).

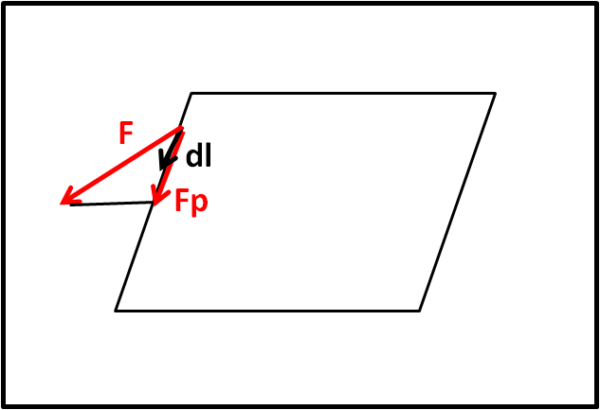
L'integrazione (di linea) calcola questo prodotto scalare per tutto il perimetro. In pratica, ci viene detto quanto campo circola  o meglio RUOTA lungo la linea CHIUSA.

Passiamo alla parte sinistra della relazione.

Consideriamo l'area racchiusa all'interno del nostro filo quadrato. Consideriamo un'area infinitesima dA all'interno del quadrato e indichiamo, come al solito, con dA il vettore normale a questo quadratino. D'altra parte, per come abbiamo definito l'operatore rotore, esso indica quanto campo ruota attorno al punto centrale della piccola area dA ed è un vettore che può avere qualsiasi direzione e verso. Tuttavia, questo vettore deve adesso essere moltiplicato scalarmente per ìl vettore dA e, ancora una volta, solo la componente parallela a quest'ultimo può dare un contributo.

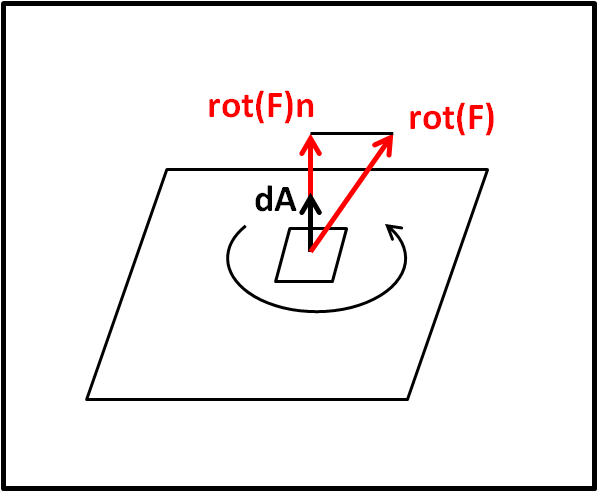
Ne segue che la rotazione del campo in quella piccola area  dA è quantificata da tutti i prodotti scalari tra vettori normali all'area.

Ma cosa succede quando andiamo a sommare tutte le aree? Ogni dA ha una sua rotazione ma le rotazioni si annullano una con l'altra, tranne che quelle dovute ai lati dei quadratini esterni, ossia rimane solo la rotazione dell'intero perimetro.

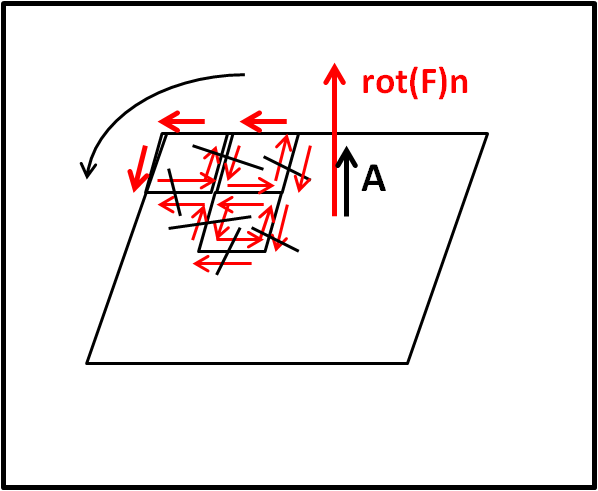
Il teorema del rotore ci dice proprio che la rotazione calcolata sul solo perimetro in modo lineare è uguale alla rotazione dell'intera area, dato che alla fine rimane solo la componente dovuta al suo perimetro.

Visione alternativa (ricordando il momento angolare) 

una carica q si sta muovendo con velocità v. Se entra in un campo magnetico la carica viene fatta deviare  da una certa forza che è  proporzionale alla carica che si muove e alla sua velocità. Ma, ovviamente deve anche essere proporzionale all'intensità del campo magnetico. L'intensità è quindi data da:

F_M = q v B

ma v e B sono vettori. Quale prodotto dobbiamo usare ? Si nota che la direzione della forza F_M è sempre ortogonale alla velocità v e al vettore del campo B. Ne segue che il movimento della carica avviene a causa di una forza che è ortogonale sia al vettore velocità che al vettore campo magnetico. Questo modo di vedere la questione è utile per comprendere proprio come un campo magnetico sia ortogonale alla superficie in cui avviene il movimento della carica. In poche parole è come se facessimo girare qualcosa attorno a un punto e volessimo indicare il suo momento angolare. La particella si muove in una certa direzione, una forza la devia ed è diretta verso il punto O: il risultato è un momento angolare che è sempre perpendicolare al piano individuato da forza agente e velocità della particella o, meglio ancora, quantità di "moto" (o di carica, dato che a mv possiamo sostituire qv)

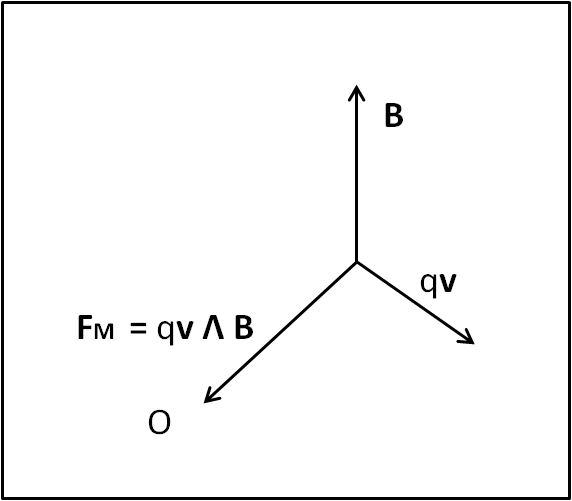
continua...