Categorie: Articoli Matematica
Tags: 3d asse di rotazione cilindro cono geometria solida parametri direttori superfici di rotazione
Scritto da: Arturo Lorenzo
Commenti:0
Geometria dello spazio - sesta parte (Esempi facili di Superfici di rotazione)
Nel mio precedente articolo ho cercato di spiegare cosa siano in geometria dello spazio le superfici di rotazione e un metodo per determinarne la rappresentazione analitica. In questo articolo fornirò una prima serie di esempi, più semplici, utilizzando ancora la possibilità di visualizzazione tridimensionale anche attraverso l'uso di occhiali anaglifici.
Rammento per comodità che una superficie di rotazione è generata dalla rotazione di una curva C attorno ad una retta r (asse). Vediamo , allora, cosa succede se la curva C è anch'essa una retta.
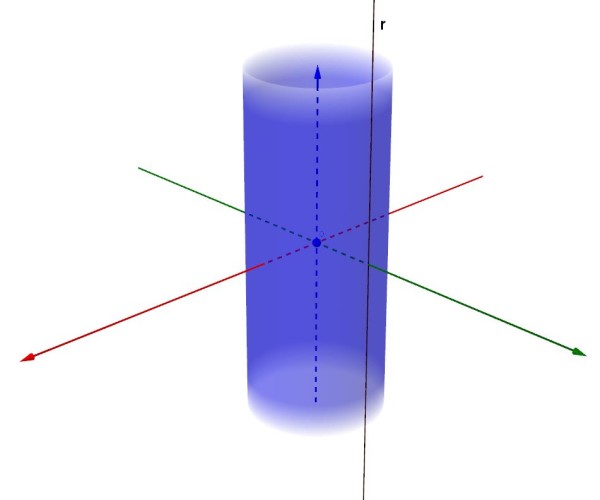
Cilindro con asse coincidente con l'asse z
In particolare, supponiamo che la curva sia una retta r parallela all'asse z del riferimento cartesiano dello spazio O,x,y,z e appartenente al piano coordinato yz. Ipotizziamo, inoltre, che l'asse attorno a cui facciamo ruotare la suddetta retta sia proprio l'asse z. Già ora, credo, starete pensando ad un cilindro avente l'asse coincidente con l'asse z. In effetti, la seguente figura illustra proprio tale entità geometrica dello spazio:
Noi, però, non ci accontentiamo della rappresentazione grafica, che potrebbe esserci regalata in modo esemplare da un artista della prospettiva come Masaccio, ma ne vogliamo determinarne l'equazione, cioè la sua rappresentazione analitica. I dati di partenza sono la rappresentazione analitica dell'asse di rotazione e della curva da far ruotare attorno all'asse. A questo proposito, ricordiamo che una qualsiasi retta dello spazio viene individuata dall'intersezione di due piani. In questo caso, trattandosi dell'asse z, i piani che intersecandosi lo generano sono il piano coordinato xz , di equazione y=0 (tutti i suoi punti, infatti, hanno coordinata y nulla) , e il piano coordinato yz, di equazione x=0 (tutti i suoi punti, infatti, hanno coordinata x nulla). Pertanto, l'asse z è rappresentato analiticamente dal sistema di equazioni:
Poi conosciamo anche la rappresentazione analitica della curva da far ruotare attorno all'asse, in questo caso una retta parallela all'asse z e appartenente al piano coordinato yz. Anche tale retta è individuata nello spazio dall'intersezione di due piani , il piano yz a cui essa appartiene e, per esempio, il piano di equazione y=4, i cui punti , quindi, hanno la stessa coordinata y pari a 4. La retta in questione, allora, è rappresentata analiticamente dal sistema di equazioni:
Applichiamo, ora, il metodo illustrato nel precedente articolo per trovare l'equazione del cilindro in questione. Come ricorderete, i passaggi da fare sono tre:
a) determinare una qualsiasi terna di parametri direttori dell'asse di rotazione. Nel caso in argomento, trattandosi dell'asse z, la terna di parametri direttori più semplice è (0,0,1)
b) considerare un qualsiasi punto appartenente alla curva che ruota intorno all'asse (nel caso in argomento, la curva che ruota è una retta di cui abbiamo già individuato le equazioni. Quindi, un suo qualsiasi punto P avrà coordinate (0, 4, zp) ] e trovare l'equazione del piano passante per P e perpendicolare all'asse di rotazione (utilizzando i parametri direttori trovati in a):
cioè
(1)
c) considerare un punto qualsiasi dell'asse di rotazione e determinare l'equazione della sfera avente centro in
e raggio pari a
. Naturalmente, poiché nel nostro caso l'asse passa per l'origine degli assi, per rendere semplici i conti, prendiamo come punto
proprio l'origine degli assi O(0,0,0). La sfera cercata, quindi, avrà equazione:
cioè, ricordando le coordinate del punto generico P della retta r:
(2)
A questo punto, mettiamo a sistema la (1) e la (2) ottenendo:
cioè, eliminando la z:
Questa è l'equazione del nostro cilindro. Se la guardiamo ponendoci sul piano coordinato xy, ci accorgiamo che essa è l'equazione della circonferenza centrata nell'origine degli assi e di raggio pari a 4. In effetti, il nostro cilindro è proprio il luogo geometrico dei punti posti a distanza pari a 4 dall'asse z, a prescindere dalla loro coordinata z.
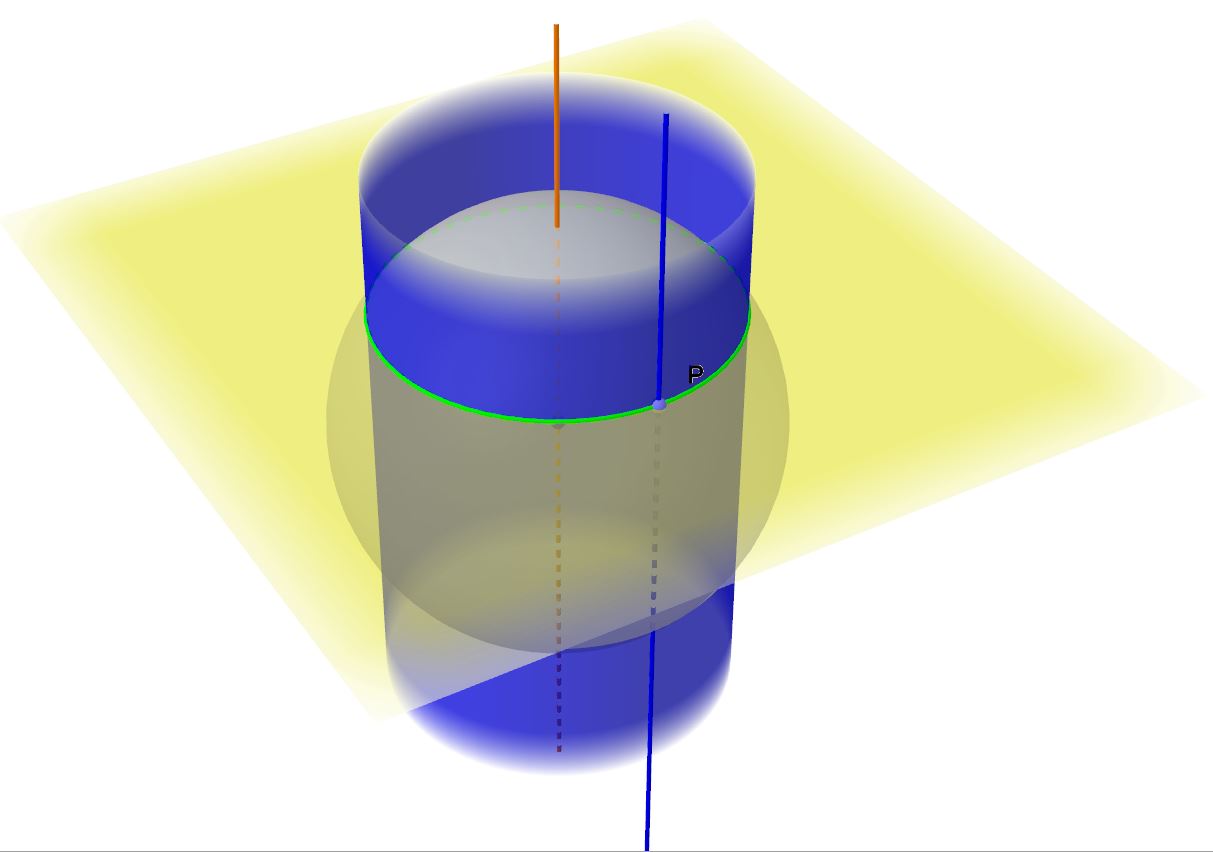
Per vedere da vicino la nostra "creatura" geometrica di rotazione, con la possibilità di osservarla come più ci aggrada, potete utilizzare il link presente nella seguente immagine. Una volta nell'applet, potete usare il vostro mouse per spostare il punto di vista da cui osservare l'oggetto geometrico rappresentato. Ci andate sopra e premete il pulsante sinistro del mouse, mantenendolo premuto. In questo modo, ad ogni spostamento del mouse corrisponderà uno spostamento dell'oggetto. Nel modello ho evidenziato il piano e la sfera , passanti per il generico punto P della retta r, dalla cui intersezione nascono le infinite circonferenze del cilindro. Consiglio, invece, di non variare nulla nella colonna che vedrete sulla sinistra. Comunque, se ad un certo punto volete ripristinare la vista iniziale, basta fare click sull'icona che vedrete in alto a destra nella pagina, quella con due freccette curve.
Se avete gli occhiali anaglifici, potete usufruire anche della visualizzazione di tipo 3D, seguendo il link presente su questa immagine. In tal caso si perdono i colori ma si ha un effetto di profondità spaziale.
E se invece la retta che ruota attorno all'asse è inclinata ? Vediamo.
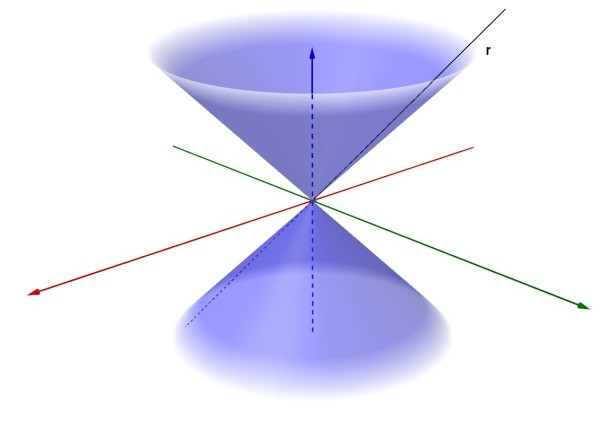
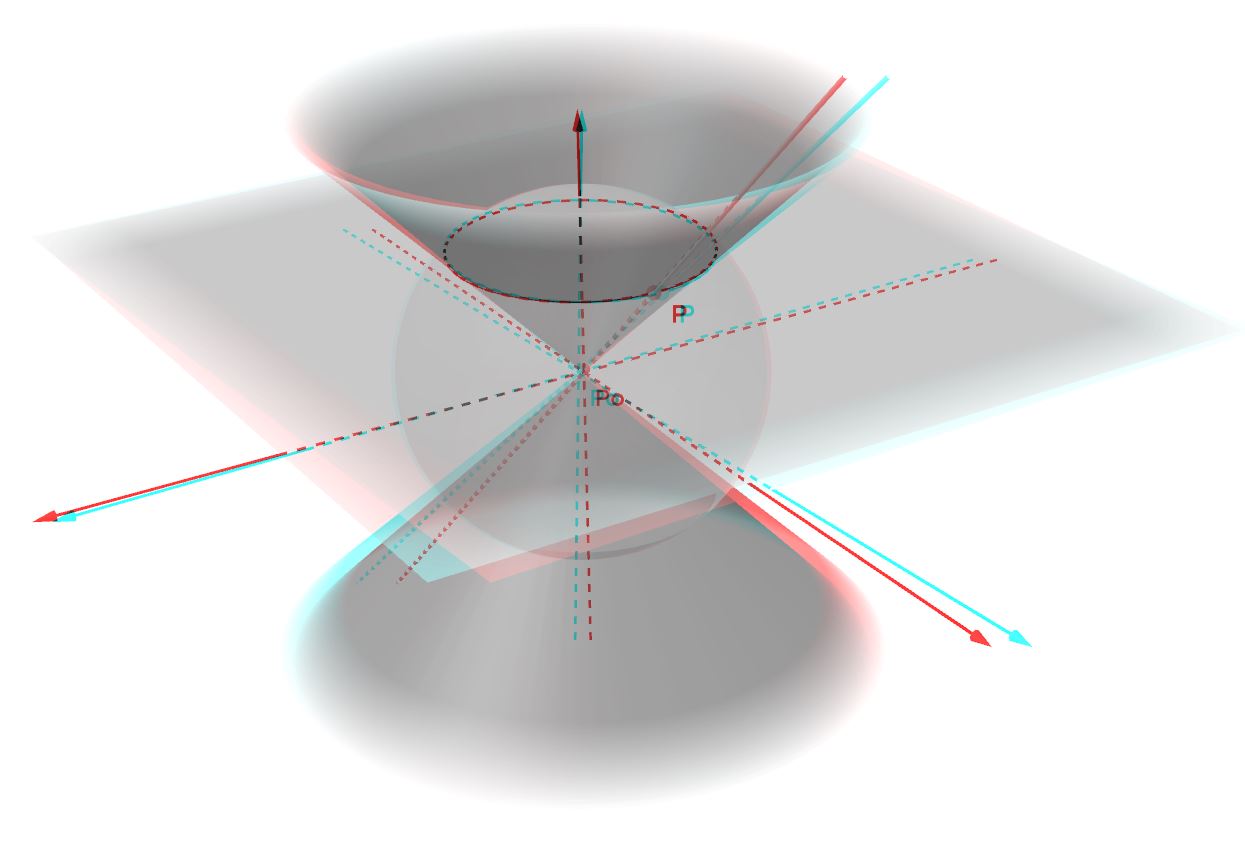
Cono con asse coincidente con l'asse z e vertice nell'origine
Anche in questo caso, per semplicità, ipotizziamo che l'asse di rotazione coincida con l'asse z. Stavolta , però, la retta che ruota attorno ad esso non è parallela all'asse di rotazione, ma inclinata rispetto ad esso. Per esempio inclinata di 45 gradi. Per semplicità, facciamola inoltre passare per l'origine degli assi cartesiani. Una tale retta è generata dall'intersezione del piano coordinato yz, di equazione x=0, e del piano passante per l'asse x e inclinato di 45 gradi rispetto al piano coordinato xy. In pratica tale secondo piano è l'equivalente nello spazio della bisettrice del primo e terzo quadrante del piano. Tutti i punti appartenenti a tale piano saranno caratterizzati dall'avere la coordinata z uguale alla coordinata y. La sua equazione sarà, dunque y=z o meglio y-z=0
La retta r che ruota attorno all'asse z , in questo caso , è dunque individuata dalle equazioni :
(3)
Ruotando attorno all'asse z, ciascun punto di tale retta r descriverà, come prima, tante circonferenze , il cui raggio, però, va diminuendo, fino ad annullarsi, man mano che ci spostiamo verso l'origine degli assi. A cosa state pensando ? Ad un cono con asse coincidente con l'asse z e vertice nell'origine. Eccolo raffigurato di seguito:
Determiniamone l'equazione.
a) determiniamo una qualsiasi terna di parametri direttori dell'asse di rotazione. Anche stavolta, trattandosi dell'asse z, la terna di parametri direttori più semplice è (0,0,1)
b) consideriamo un qualsiasi punto appartenente alla curva che ruota intorno all'asse (nel caso in argomento, la curva che ruota è una retta di cui abbiamo già individuato le equazioni. Quindi, un suo qualsiasi punto P avrà coordinate (0, zp, zp) , per le (3) ] e trovare l'equazione del piano passante per P e perpendicolare all'asse di rotazione (utilizzando i parametri direttori trovati in a):
cioé:
(4)
c) considerare un punto P0 qualsiasi dell'asse di rotazione e determinare l'equazione della sfera avente centro in e raggio pari a
. Naturalmente, poiché anche stavolta l'asse passa per l'origine degli assi, per rendere semplici i conti, prendiamo come punto
proprio l'origine degli assi O(0,0,0). La sfera cercata, quindi, avrà equazione:
cioè, ricordando le coordinate del punto generico P della retta r:
cioé:
quindi:
Questa è, dunque, l'equazione del nostro cono. Anche stavolta, se portiamo a secondo membro il termine con la z e osserviamo il primo membro, ci accorgiamo che , preso sul cono un qualsiasi punto P (x,y,z) e considerandone la proiezione ortogonale sul piano coordinato xy, l'equazione ci dice che il segmento
è uguale al segmento
. Infatti, la lunghezza del segmento
è proprio pari a
, mentre la lunghezza del segmento
è pari a z. Quindi, il triangolo
è isoscele con angoli alla base di 45 gradi, essendo l'angolo in
retto. Non poteva essere altrimenti, visto che abbiamo generato il cono facendo ruotare attorno all'asse z una retta, passante per l'origine, inclinata di 45 gradi rispetto al piano xy .
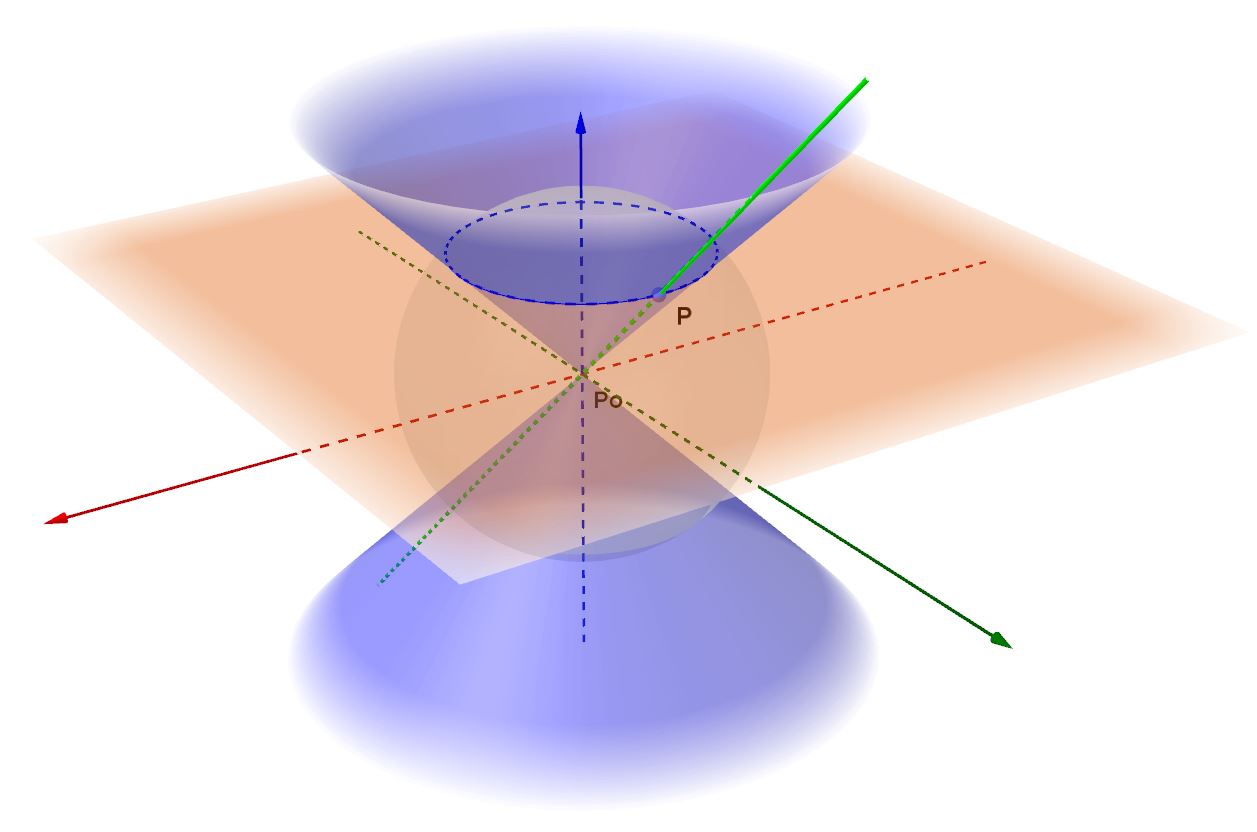
Anche ora, per vedere da vicino la nostra seconda creatura geometrica di rotazione, con la possibilità di osservarla come più ci aggrada, potete utilizzare i links presenti nelle seguenti due immagini, con le avvertenze e le istruzioni già viste prima.
Nel prossimo articolo vedremo cosa viene fuori facendo ruotare attorno all'asse z una retta sempre inclinata di 45 gradi rispetto al piano coordinato xy, ma non passante per l'origine.