Geometria dello spazio - quinta parte (Superfici di rotazione)

In questo articolo faremo la conoscenza di una particolare entità geometrica spaziale che ritroviamo in molti esempi della realtà che ci circonda: la superficie di rotazione. Vedremo, inoltre, come ricavarne la rappresentazione analitica.

Come si intuisce dal suo stesso nome, tale entità geometrica è generata dalla rotazione di una curva attorno ad una retta, detta asse della superficie. In particolare, definiamo superficie di rotazione la rappresentazione grafica, in un riferimento cartesiano dello spazio, del luogo geometrico descritto dalla rotazione di una curva C intorno ad una retta r. Abbiamo già incontrato nei precedenti articoli il concetto di luogo geometrico. Esso è l'insieme dei punti dello spazio le cui coordinate soddisfano una data condizione. Per esempio, la sfera è il luogo geometrico dei punti equidistanti da un punto dato, detto centro della sfera. Quindi, se indichiamo con $(x_{P},y_{P},z_{P})$ le coordinate del generico punto P del luogo geometrico, con $(x_{o},y_{o},z_{o})$ le coordinate del centro Po e con R la distanza (costante) tra P e Po, in questo caso la condizione da soddisfare è:

$(x_{P}-x_{o})^{2}+(y_{P}-y_{o})^{2}+(z_{P}-z_{o})^{2}=R^{2}$

In generale, la condizione che deve essere soddisfatta da tutti i punti P(x, y, z) di un luogo geometrico può essere espressa dall'equazione

f(x, y, z) = 0 (1)

dove f indica la funzione delle variabili x, y, z ed esprime la condizione specifica di quel luogo geometrico.

Il fatto che ciascuno dei punti di un luogo geometrico nello spazio abbia coordinate x,y,z tra loro collegate dalla (1) significa che tale punto non può occupare tutte le possibili $\infty ^{3}$ posizioni dello spazio, ma solo $\infty ^{2}$ posizioni. Infatti, una volta fissate due delle tre coordinate del punto, la terza coordinata è univocamente stabilita attraverso la (1). Sotto certe ipotesi di continuità e derivabilità della funzione f, l'insieme dei punti reali dello spazio le cui coordinate soddisfano la (1) si definisce superficie nel senso intuitivo del termine. Detta superficie è, in pratica, l'equivalente geometrico della rappresentazione analitica espressa dalla (1). Perché la precisazione "nel senso intuitivo del termine" ? Perché , in generale, possono esserci anche superfici aventi solo un numero finito di punti reali o addirittura prive di punti reali e costituite solo da punti immaginari, ossia punti aventi coordinate complesse che soddisfano la (1). In questo articolo, tuttavia, avremo a che fare solo con superfici reali o, in ogni caso, ci interesseremo solo della parte reale di tali superfici.

Analoghe considerazioni possono farsi nel piano. In tal caso, la condizione che deve essere soddisfatta da tutti i punti P(x, y) di un luogo geometrico nel piano può essere espressa dall'equazione:

f(x,y) = 0 (2)

Anche ora, riducendosi in questo caso le variabili a 2, il fatto che ciascuno dei punti di un luogo geometrico nel piano abbia coordinate x,y tra loro collegate dalla (2) significa che tale punto non può occupare tutte le possibili $\infty ^{2}$ posizioni del piano, ma solo $\infty ^{1}$ posizioni. Infatti, una volta fissata una delle due coordinate del punto, la seconda coordinata è univocamente stabilita attraverso la (2). Anche ora, sotto certe ipotesi di continuità e derivabilità della funzione f, l'insieme dei punti reali del piano le cui coordinate soddisfano la (2) si definisce curva nel senso intuitivo del termine, con la stessa precisazione fatta prima a proposito delle superfici. Possono, infatti, esserci curve con punti reali e punti immaginari o con soli punti immaginari. Anche qui, considereremo solo curve reali. La curva così intesa è, in pratica, l'equivalente geometrico della rappresentazione analitica espressa dalla (2).

Tornando dal piano allo spazio, una curva sarà analiticamente definita dal sistema di due equazioni come la (1), cioè:

f(x,y,z,)=0 (3)

g(x,y,z)=0 (4)

Essa, cioè , sarà intesa come intersezione tra due superfici. Un discorso, in fondo già visto in uno degli articoli precedenti, dove si era definita la retta nello spazio come intersezione tra due piani.

Nel caso delle curve nello spazio, tuttavia, può accadere che le due superfici le cui equazioni sono la (3) e la (4), oltre ad avere la curva come intersezione, abbiano anche altri punti in comune o addirittura altre curve.

Una curva, inoltre, può essere piana , quando esiste un piano che la contiene, oppure sghemba nel caso contrario. Esempi familiari di curve piane sono la retta, la circonferenza, la parabola, l'ellisse, l'iperbole... Esempio di curva sghemba, invece, è l'elica cilindrica. La vedete, colorata di verde, nella seguente animazione, in cui, per evidenziarne la spazialità, ho inserito un punto di colore blu che si muove lungo essa.

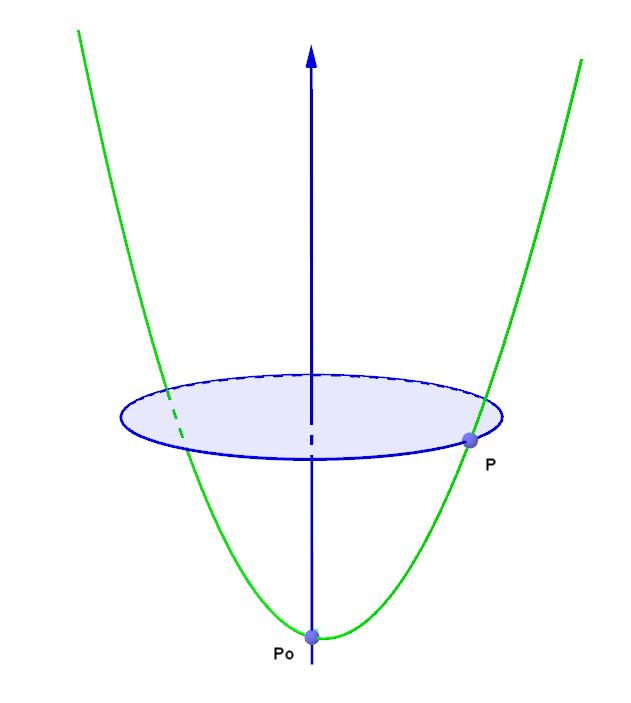
Tornando ora alla definizione di superficie di rotazione, è evidente, come illustra la figura seguente, che, data una curva (in questo caso una parabola) e una retta r (asse) attorno alla quale farla ruotare, ciascun punto P della curva data , ruotando attorno all'asse , descriverà una circonferenza. Tale circonferenza apparterrà ad un piano perpendicolare all'asse di rotazione ed avrà il proprio centro sull'asse medesimo.

Spostandoci lungo la curva e ripetendo la rotazione, otterremo tante circonferenze , che altro non sono che sezioni trasversali della nostra superficie di rotazione. Tali circonferenze si definiscono "paralleli" della superficie di rotazione (il riferimento ai paralleli del globo terrestre è immediato). Sezionando, invece, la superficie di rotazione con piani passanti per l'asse di rotazione, si ottengono evidentemente curve tutte uguali a quella di partenza. Tali curve si definiscono "meridiani" della superficie di rotazione, come era facile prevedere.

Il nostro obiettivo è ora determinare l'equazione , ossia la rappresentazione analitica, di una superficie di rotazione S generata dalla rotazione di una curva C attorno ad una retta (asse) r.

Consideriamo un qualsiasi punto $P_{o}(x_{o},y_{o},z_{o})$ appartenente alla retta r. Sia, inoltre, (a, b, c) una terna di parametri direttori della retta r, di cui abbiamo parlato nel precedente articolo. Sia, infine $P(x_{P},y_{P},z_{P})$ il generico punto della superficie di rotazione. Rammentando quanto illustrato nel precedente articolo, il piano passante per $P$ e perpendicolare alla retta r sarà dato dall'equazione:

$a(x-x_{P})+b(y-y_{P})+c(z-z_{P})=0$ (5)

La sfera avente centro in $P_{o}$ e raggio $\overline{PP}_{o}$ , invece, avrà equazione:

$(x-x_{o})^{2}+(y-y_{o})^{2}+(z-z_{o})^{2}=(x_{P}-x_{o})^{2}+(y_{P}-y_{o})^{2}+(z_{P}-z_{o})^{2}$ (6)

essendo il termine al secondo membro la distanza tra i punti $P$ e $P_{o}$ elevata al quadrato.

Ormai avrete intuito che le circonferenze di cui si diceva sopra vengono ottenute come intersezione tra il piano di equazione (5) e la sfera di equazione (6), al variare di P lungo la curva data.

Infine, il generico punto $P(x_{P},y_{P},z_{P})$ della curva , in quanto appartenente alla curva, deve soddisfare il sistema di equazioni della curva:

$f(x_{P},y_{P},z_{P})=0$ (7)

$g(x_{P},y_{P},z_{P})=0$ (8)

Potendosi, per quanto si è detto sopra, considerare la superficie di rotazione S come il luogo geometrico delle circonferenze perpendicolari all'asse e al variare del punto P lungo la curva, l'equazione di S si potrà, allora, ricavare attraverso il sistema delle (5), (6), (7) e (8).

Come sempre, un esempio aiuta molto ai fini della comprensione dei concetti.

Consideriamo la curva nello spazio rappresentata dalle equazioni (è un'iperbole equilatera giacente nel piano xy)

xy=1 (7)

z=0 (8)

Sia data la retta r nello spazio data dalle equazioni (è una retta passante per l'origine , inclinata di 45 gradi rispetto all'asse x e giacente sul piano xy) :

x-y=0

z=0

Un punto $P_{o}(x_{o},y_{o},z_{o})$ di tale retta è, per esempio, l'origine degli assi. Una terna di parametri direttori della retta r sarà in questo caso (1, 1, 0). L'equazione del piano passante per il generico punto P della curva e perpendicolare ad r sarà, quindi:

$1*(x-x_{P})+1*(y-y_{P})+0*(z-z_{P})=0$

cioè:

$(x-x_{P})+(y-y_{P})=0$

ossia:

$x+y=x_{P}+y_{P}$ (5)

La sfera con centro in Po (= origine degli assi) e raggio $\overline{PP}_{o}$ ha, in questo caso, equazione:

$x^{2}+y^{2}+z^{2}=x_{P}^{2}+y_{P}^{2}$ (6)

Per il generico punto P della curva, infine, dovranno essere verificate le equazioni

$x_{P}*y_{P}=1$ (7)

$z_{P}=0$ (8)

Mettendo a sistema le (5), (6), (7) e (8), eliminando i parametri $x_{P},y_{P},z_{P}$ , alla fine si ottiene:

$z^{2}-2xy+2=0$

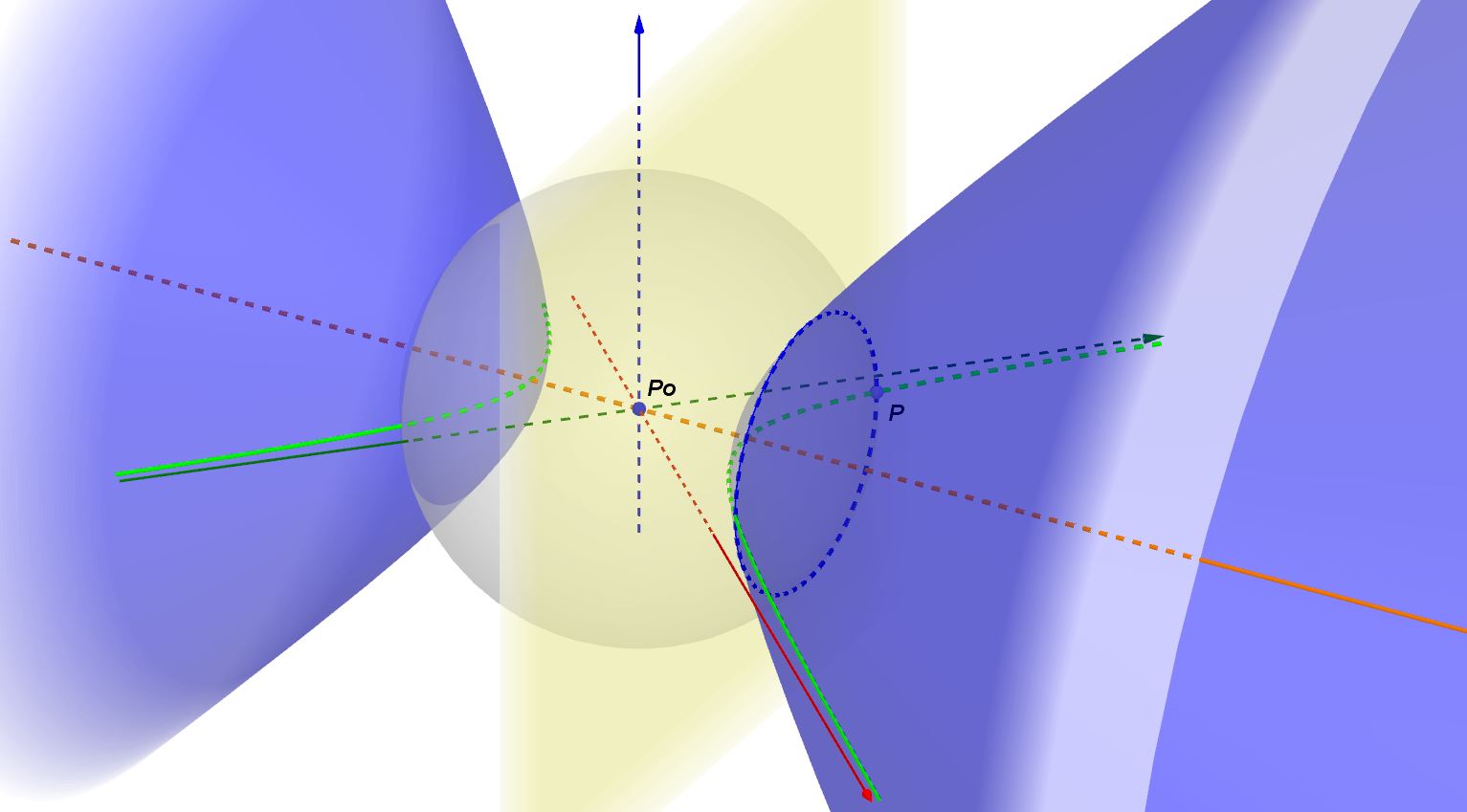
L'equazione ottenuta è quella di un iperboloide di rotazione, illustrato nella seguente figura. In essa ho mantenuto visibili la circonferenza (di colore grigio semitrasparente) e il piano (di colore giallo semitrasparente), dalla cui intersezione, al variare del generico punto P, si ottengono le varie sezioni trasversali della superficie di rotazione (circonferenza tratteggiata di colore blu).

Credo che la figura sia sufficientemente esplicativa. Ma, visto che siamo nello spazio, che ne direste di visualizzare l'iperboloide di rotazione con un paio di occhialetti 3D , di quelli con una lente rossa e una ciano (occhiali anaglifici) ?

Ebbene, basta procurarvene un esemplare , se ne trovano agevolmente anche in Rete a pochi euro, e osservare la seguente animazione (suggerita la visione a schermo intero). Attenzione a non illudervi troppo della spazialità di ciò che vedrete, tra voi e l'iperboloide continua ad esserci il monitor del computer... :-)

Nel prossimo articolo illustreremo un po' di altri esempi di superfici di rotazione. Applicando il metodo illustrato in questo articolo per ricavarne l'equazione, non resta che sbizzarrirsi con la fantasia...

---

Quelli che seguono sono i links a tutti gli articoli di geometria solida sinora pubblicati, prima di questo:

L	M	M	G	V	S	D
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

Geometria dello spazio - quinta parte (Superfici di rotazione)

Articoli correlati

Soluzione del "banale" esponente **

(Q) Un semplice esponente ... **

Soluzioni dello scontro evitato **/***

Evitiamo uno scontro **/***

Lascia un commento Cancel Reply

Soluzioni dello scontro evitato /*

Evitiamo uno scontro /*