Categorie: Matematica
Tags: Brunelleschi cerchi di Villarceau geometria dello spazio geometria solida ippopede di Proclo Lemniscata di Bernoulli lemniscata di Booth ovali di Cassini toro toroide
Scritto da: Arturo Lorenzo
Commenti:2
Geometria solida- Il Toro - Appendice 1 alla parte 8°: Circonferenze di Villarceau, Ippopede di Proclo, Lemniscate e altre prelibatezze... ***
Circonferenze di Villarceau
Nel mio ultimo articolo, visibile QUI, in cui abbiamo fatto la conoscenza di quella particolare superficie di rotazione che è il toro, avevamo, tra l'altro, ricavato la rappresentazione analitica di alcune sezioni del toro realizzate con piani secanti particolari. Avevo illustrato che, considerando un toro di raggio minore r e raggio maggiore R, con centro nell'origine degli assi e asse di rotazione coincidente con l'azze z, sezionandolo con il piano xy si ottengono due circonferenze concentriche centrate nell'origine e di raggio (R-r) ed (R+r). Avevo omesso di precisare, lo faccio ora, che due circonferenze analoghe risultano anche dalla sezione del toro suddetto con un qualsiasi piano parallelo al piano xy purché avente distanza da questo minore di r, sia nel verso positivo dell'asse z sia in quello negativo.

Sempre nel precedente articolo avevo illustrato anche che, con riferimento al solito toro, se lo sezioniamo con un piano passante per l'asse z otteniamo altre due circonferenze , simmetriche rispetto all'asse z, di raggio r e centro giacente a sua volta sulla circonferenza appartenente al piano xy, con centro nell'origine e raggio R.
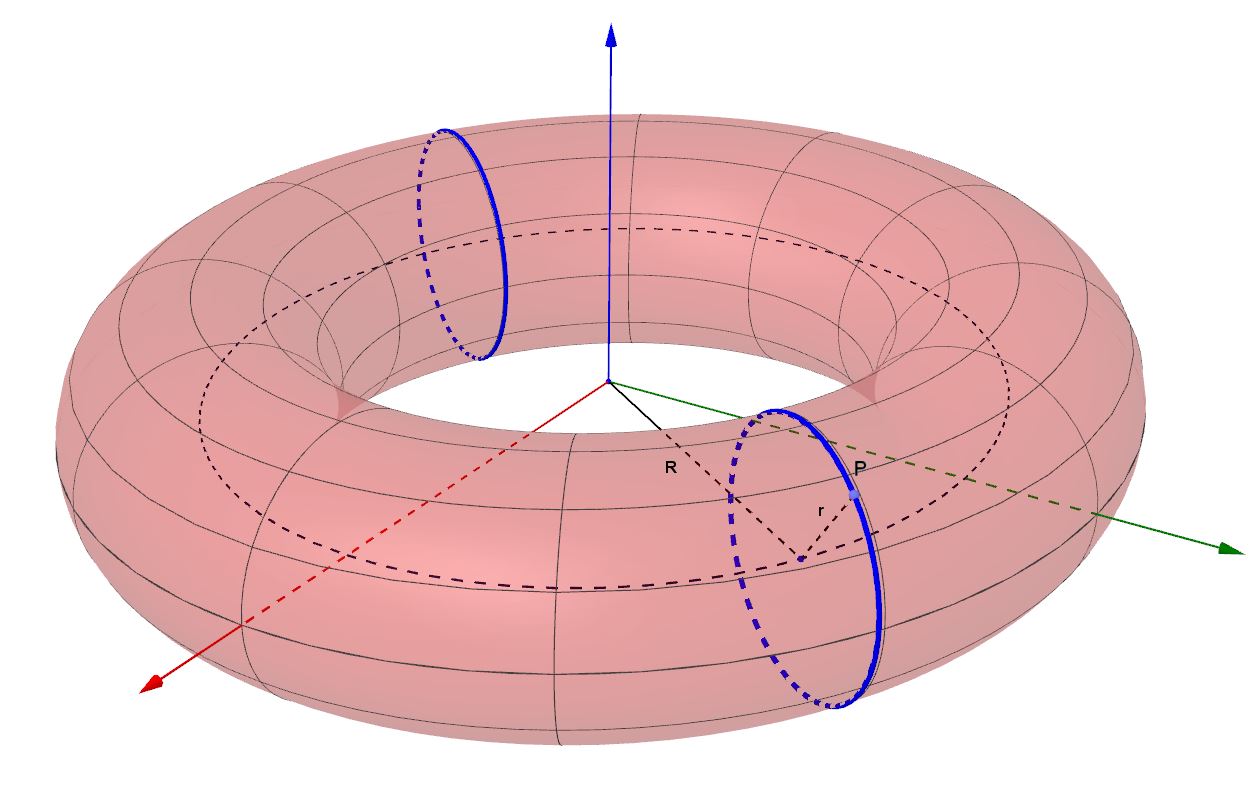
Se tanto mi dà tanto, uno potrebbe concludere che, dato un qualsiasi punto P appartenente alla superficie del toro, per esso passano solo due circonferenze, una, che abbiamo chiamato meridiano, di raggio r, e una, che abbiamo chiamato parallelo, con centro sull'asse z nel punto C di coordinate 0,0,z(P), parallela al piano xy e di raggio pari alla quantità .
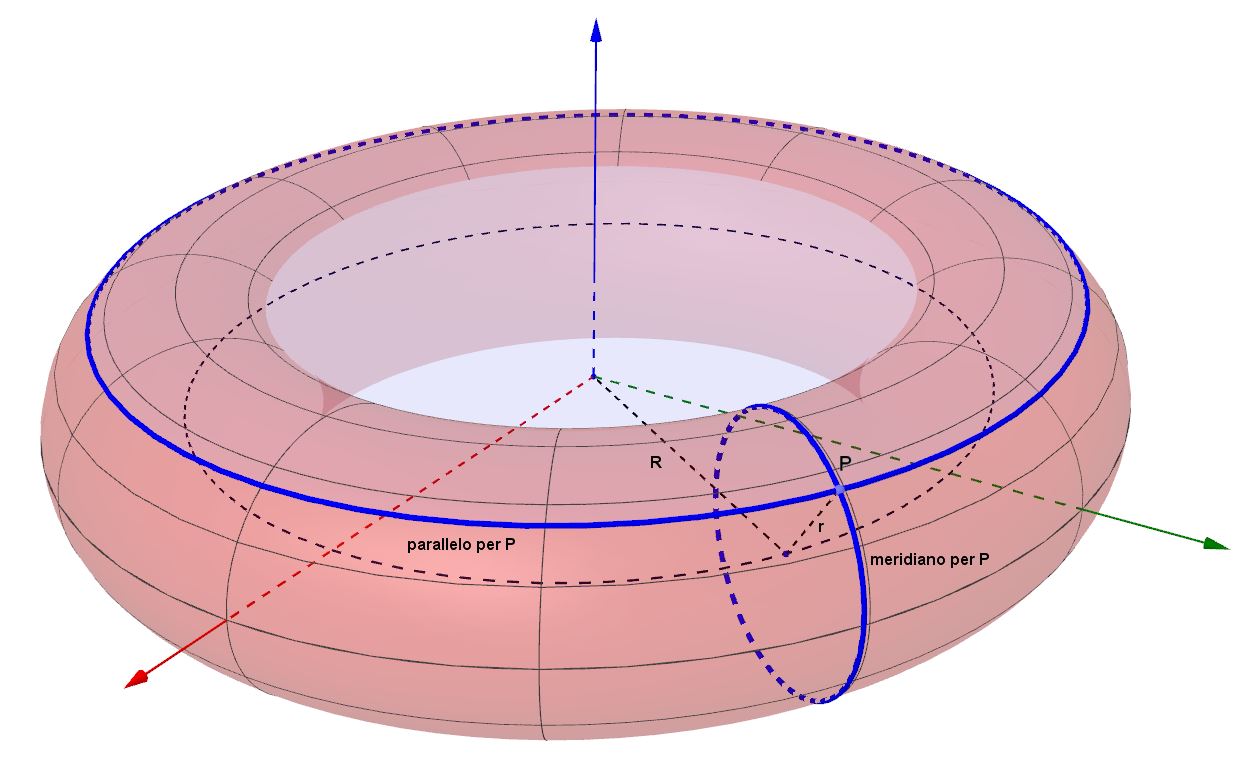
Sbagliato ! Di circonferenze per un qualsiasi punto P del toro in realtà ne passano quattro ! ![]()
Ora vedremo di ricavare l'equazione delle altre due e dimostreremo che si tratta proprio di circonferenze. Intanto vi anticipo il loro nome: "circonferenze di Villarceau", dal nome dell'astronomo francese Antoine-Joseph Yvon Villarceau (1813-1883) che teorizzò la loro esistenza. Qui potete leggere l'estratto di una nota in cui l'astronomo comunicava il teorema:

Nonostante il discorso valga per qualsiasi punto P del toro, per facilitare le cose consideriamo il punto P esterno di intersezione tra il toro e il semiasse positivo delle asse x, quindi avente coordinate cartesiane (R+r, 0, 0). Facciamo riferimento alla seguente figura. Consideriamo ora il piano passante per l'asse x (quindi anche per il punto P) e tangente alla superficie del toro. Indichiamo con l'angolo compreso tra tale piano e il piano xy
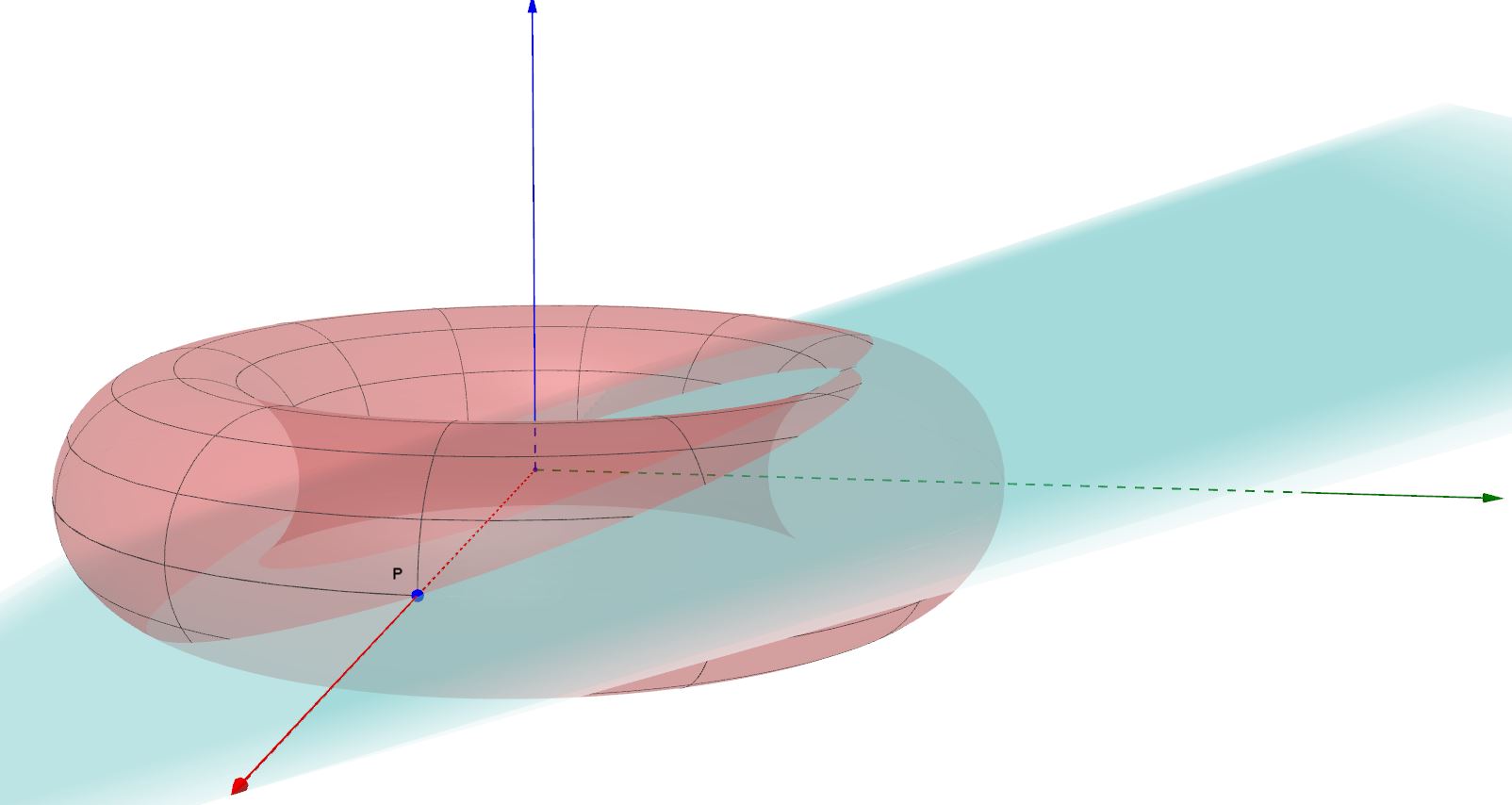
Osserviamo ora il toro, con il suddetto piano secante, in proiezione ortogonale parallela all'asse x (il vettore dell'asse x viene verso di noi).
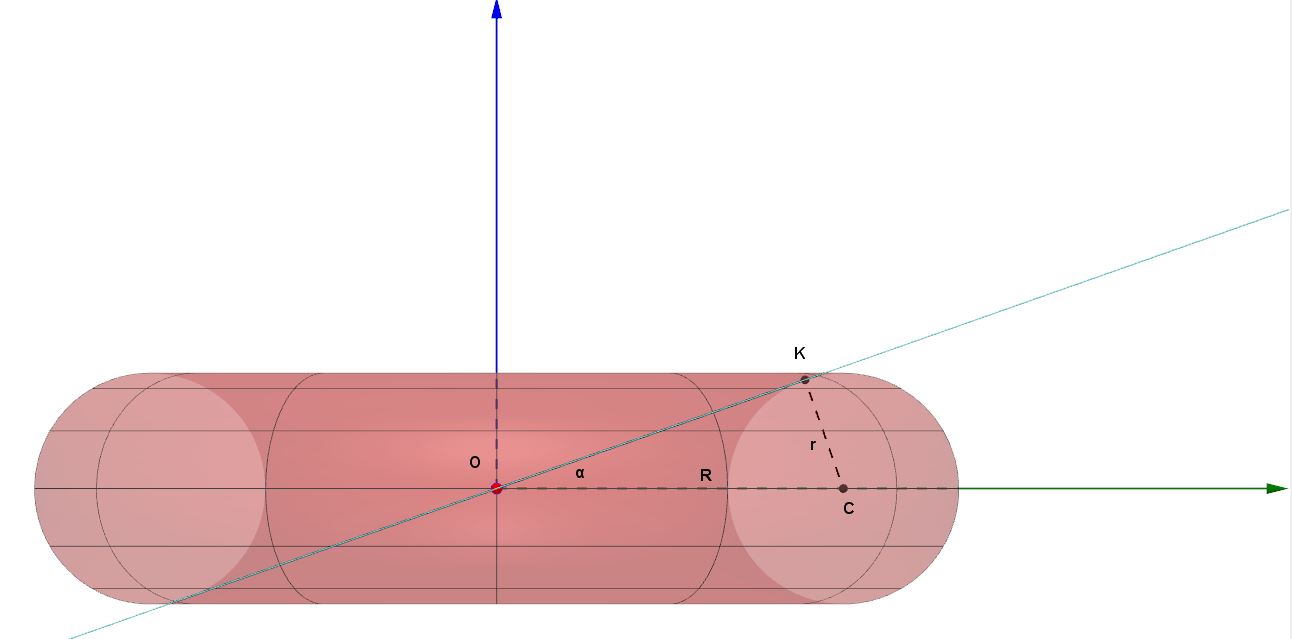
Poiché il piano è tangente al toro, con riferimento al triangolo OKC, avremo che esso è rettangolo e quindi, per il teorema di Pitagora:
(1)
Inoltre, per i teoremi trigonometrici dei triangoli rettangoli:
(2)
da cui, mettendo assieme la (1) e la (2):
cioè:
(3)
Il nostro obiettivo è ricavare l'equazione della curva di intersezione tra il toro e il suddetto piano inclinato. Poiché , inoltre, vogliamo dimostrare che si tratta di circonferenze appartenenti al piano secante, è utile ricavare la loro equazione riferita al sistema di riferimento del piano. Tale sistema, per come abbiamo scelto il piano, ha l'asse x invariante e gli assi y e z ruotati di un angolo attorno all'asse x. In pratica, per passare dal sistema di riferimento O,x,y,z al sistema O,x',y',z', basta applicare le formule della rotazione attorno all'asse x di un angolo
:
(4)
Vediamo, dunque, l'aspetto assunto in tale nuovo sistema di riferimento dall'equazione cartesiana del toro e da quella del piano secante.
Per il piano è immediato ricavare che la sua equazione nel nuovo sistema di riferimento è semplicemente
(5)
Infatti, tutti i punti del piano, nel sistema di riferimento ruotato hanno coordinata z' nulla.
Per il toro, invece, ricordo che l'equazione cartesiana ricavata nel precedente articolo é:
Basta ora sostituire in essa le x,y,z con le rispettive espressioni risultanti dalle (4) e tenere conto della (5), visto che cerchiamo l'intersezione tra toro e piano . Svolgendo i calcoli, rammentando che , alla fine otteniamo:
cioè, per la (3):
Portiamo ora il termine con la radice al secondo membro ed eleviamo al quadrato primo e secondo membro:
cioè:
cioè:
Ora, a secondo membro, aggiungo e sottraggo il termine . Spostando al primo membro, sommando i termini simili e ordinando opportunamente otteniamo:
che possiamo anche scrivere come:
cioè:
Ci troviamo difronte ad una differenza di quadrati, che possiamo dunque sviluppare come prodotto notevole:
cioè:
Ordiniamo e scriviamo:
(6)
Ricordando che l'equazione cartesiana di una circonferenza nel piano xy è:
è allora immediato riconoscere nella (6) due circonferenze aventi
quindi con centri (di coordinate-a/2 e -b/2)
e raggio pari ad R.
Tali circonferenze di Villarceau sono colorate in blu nella seguente figura.
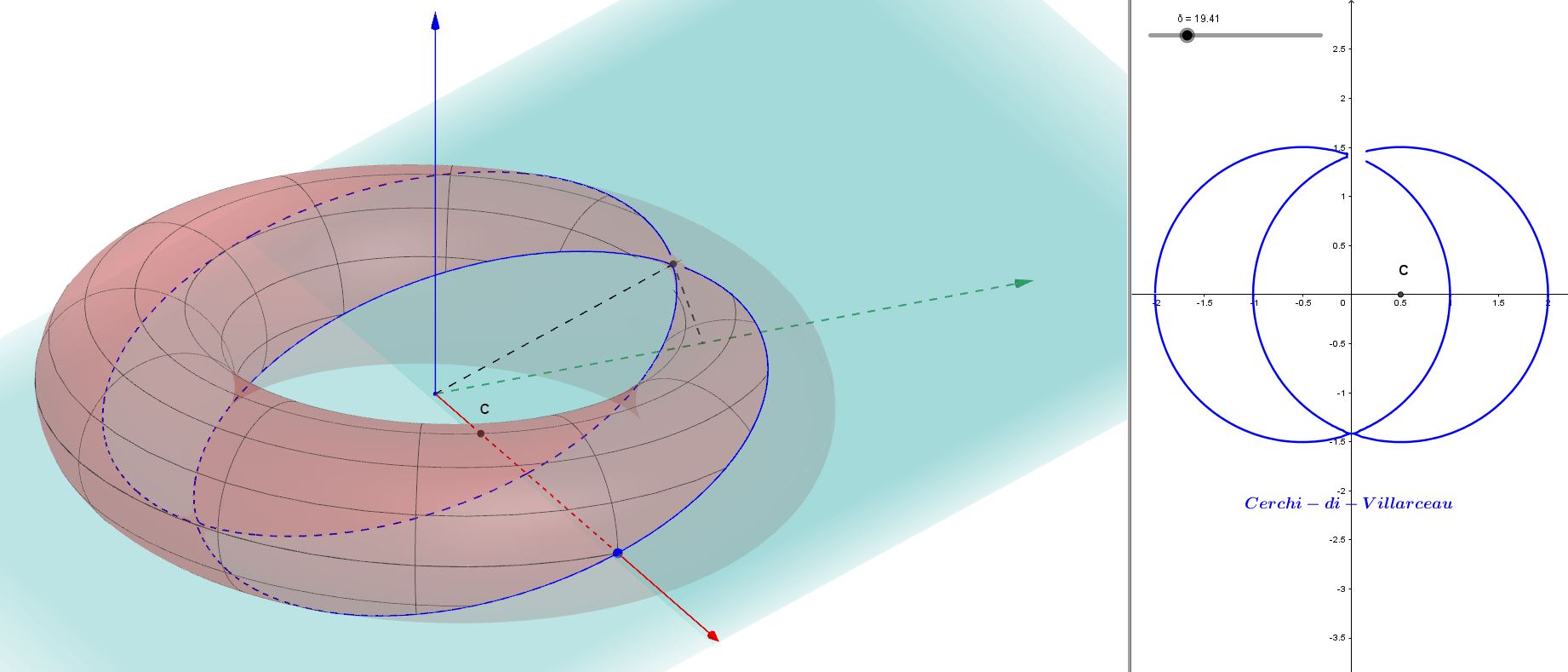
Nella parte a destra delle figura ho raffigurato le due circonferenze di Villarceau come visibili nel sistema di riferimento del piano bitangente. Ho evidenziato il centro C di una di esse, quella passante per il punto P.
Resta, dunque, confermato, che, con riferimento alla seguente figura, per il punto P scelto all'inizio passano non solo due circonferenze ma quattro, una parallela al piano xy (parallelo, colorato in blu) , una appartenente al piano passante per l'asse z e per il punto P (meridiano, colorato in rosso) e una delle circonferenze di Villarceau ricavate sopra (colorata in verde). La quarta (colorata in giallo) è quella simmetrica a quest'ultima rispetto al piano meridiano .
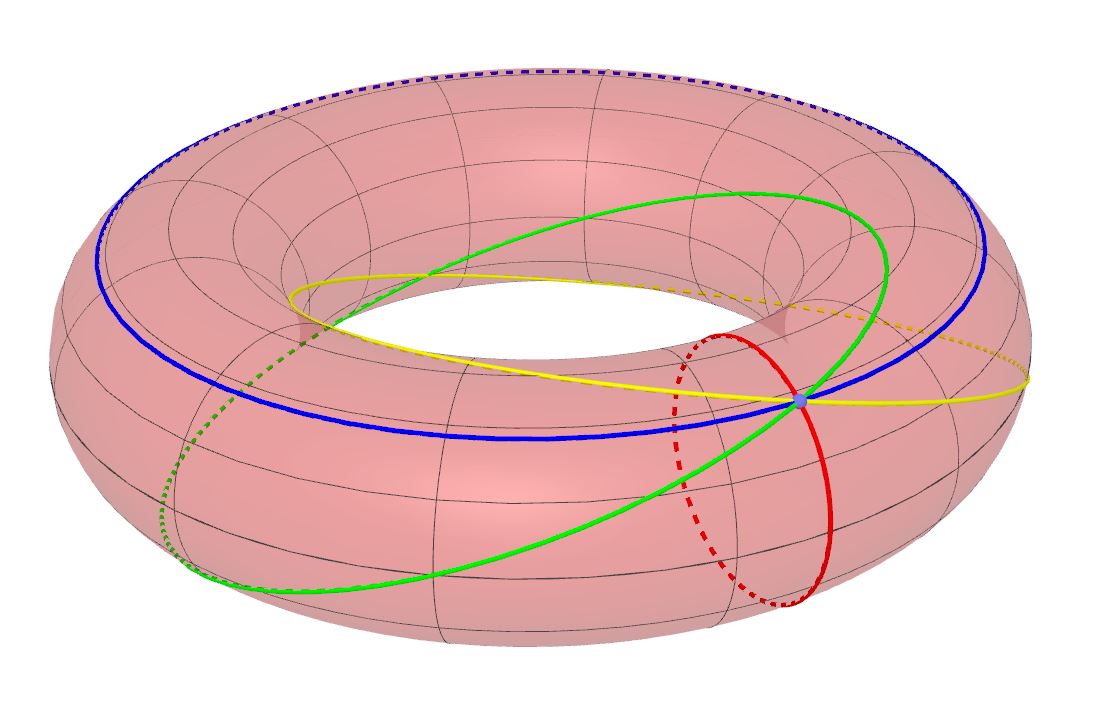
Per convincerci del fatto che ciò vale per qualsiasi punto P posto sulla superficie del toro, e non solo per il particolare punto P preso in considerazione nel suddetto ragionamento, pensiamo nel modo seguente. Immaginiamo , intanto, di spostare il punto P scelto all'inizio lungo il parallelo del toro passante per esso. E' ovvio che per motivi di simmetria del toro (è una superficie di rotazione) potremmo rifare l'identico ragionamento fatto sopra prendendo in considerazione un sistema di riferimento ruotato attorno all'asse z esattamente come il punto P. Troveremo la stessa espressione delle circonferenze di Villarceau. E se, invece, spostassimo il punto P a piacere sulla superficie del toro ? In questo caso immaginiamo di far ruotare attorno all'asse z le circonferenze di Villarceu trovate prima. Potremo sempre, per qualsiasi nuova posizione del punto P sul toro, trovarne una che passa proprio per P.
In definitiva, dato un qualsiasi punto P sul toro, scegliendo opportunamente il piano secante passante per tale punto, è sempre possibile trovare una circonferenza di Villarceau che passa per P.
A proposito delle circonferenze di Villarceau, consentitemi una digressione storiografica e una artistica.
La loro esistenza si intreccia curiosamente con due grandi nomi della Fisica italiana: Emilio Segré ed Ettore Majorana. Pare che una volta Emilio Segré raccontò che, in occasione di uno dei suoi esami universitari, mentre aspettava di essere chiamato per l'interrogazione, Majorana, suo compagno di studi, gli dette una prova sintetica dell'esistenza delle circonferenze di Villarceau su un toro. Segré lì per lì non la capì del tutto, ma la memorizzò. Quando entro' nell'aula d'esame, il suo professore Pittarelli gli chiese, come era sua abitudine, se avesse preparato un argomento particolare. Segré rispose di si e illustrò proprio l'esistenza delle circonferenze di Villarceau, ripetendo la dimostrazione che Majorana gli aveva esposto poco prima. Il suo professore rimase colpito e si congratulò per quella dimostrazione così elegante, che non conosceva.
Che io sappia, la dimostrazione di Ettore Majorana non è stata mai pubblicata da alcuno. Chissà come sarebbe stato interessante leggerla.
Le circonferenze di Villarceau, inoltre, si incontrano anche nell'architettura. Qui di seguito un esempio molto bello, visibile sulla scala del Museo dell'Opera di Notre-Dame a Strasburgo (secolo XVI)

Ma pare che anche il grande Filippo Brunelleschi abbia usato delle circonferenze di Villarceau per la volta della Cappella Pazzi a Firenze!

Chi volesse approfondire questo aspetto trova una interessantissima lettura QUI
Ma non è finita qui. Nella prossima parte di questa appendice, faremo la conoscenza di alcune cosiddette sezioni spiriche del toro : l'Ippopede di Proclo, gli ovali di Cassini, la lemniscata di Booth e quella di Bernoulli.
---
Quelli che seguono sono i links a tutti gli articoli di geometria solida sinora pubblicati, prima di questo:
- Introduzione alla geometria dello spazio (parte prima)
- Introduzione alla geometria dello spazio (parte seconda)
- Introduzione alla geometria dello spazio (appendice)
- Geometria dello spazio (parte terza)
- Geometria dello spazio (parte quarta)
- Geometria dello spazio (parte quinta)
- Geometria dello spazio (parte sesta)
- Geometria dello spazio (parte settima - altri esempi di superfici di rotazione )
- Geometria dello spazio (parte ottava - il toro)
Li trovate anche nell'ARCHIVIO






2 commenti
Lavoro veramente prezioso... (e con Brunelleschi di mezzo non si scherza). E' quasi inutile dire che il toro la fa da padrone anche nelle proiezioni topologiche dell'ipersfera. Ma noi non esagereremo in tal senso...
E pensare che in Spagna continuano a sacrificarli nelle corride...

Grazie Vincenzo.
Approfitto per dire che , naturalmente, se qualcuno dei lettori ha dubbi da sciogliere o chiarimenti da chiedere si senta libero di farlo. Per quanto mi è possibile, resto volentieri a disposizione.