Ho cercato il modo migliore per introdurre due numeri (o -meglio- concetti) fondamentali per la matematica, la geometria e la fisica. Ho trovato varie possibilità, anzi potrei dire che ne ho trovato infinite. E, allora, mi sono fermato se no rischiavo di mordermi la coda (che non ho… ve lo giuro!). Ho quindi deciso di agire a modo mio. L’importante è che alla fine si riesca a comprendere con chi abbiamo a che fare.

Sicuramente è il concetto più difficile da definire senza usare una matematica già abbastanza sofisticata. Tuttavia, per comprendere una matematica di un certo livello è necessario aver introdotto il concetto di infinito. Un bel problema. Ho deciso, quindi di lasciare la formulazione matematica per ultima.

Essendo noi degli appassionati dell’Universo, dovremmo forse partire dalla definizione fisica. Quante volte abbiamo parlato di Cosmo infinito. Ricordiamoci, però, che abbiamo anche dimostrato che un Universo finito può anche essere considerato  infinito dato che non esiste niente al di fuori di esso. Temo che anche il pensare a qualcosa di grande, immenso, rischi alla fine di creare dei “limiti” alla comprensione. E parlare di infinito con dei… limiti diventerebbe assurdo.

Un punto reale ma irraggiungibile

Alla fine ho deciso di partire con la geometria. Non che sia più facile discutere di geometria, anzi non solo ha i problemi della matematica, ma tutta una serie di strane applicazioni per trasformare ciò che esiste in tre dimensioni nella sua migliore rappresentazione in due soltanto, ossia il piano del foglio. Tuttavia, la geometria ha un enorme vantaggio: il concetto di infinito è immediatamente sotto gli occhi di tutti. Cosa che non capita per l’Astronomia, dove per vedere l’infinito siamo costretti a immaginare ed estrapolare qualcosa. Nella geometria, invece, l’infinito è lì, davanti a noi, basta sapere dove cercare.

Ricordiamoci una delle definizioni più semplici e utilizzate, che conoscono perfino i bambini più piccoli: “Due rette parallele non si incontrano mai”. Non è un concetto difficile da capire e da provare direttamente. Basta munirsi di un “metro” e andare lungo una linea ferroviaria (meglio se in disuso in modo da essere sicuri che non passino treni). Se non abbiamo paura di camminare un po’, possiamo facilmente misurare la distanza tra le due rotaie in punti diversi, anche molto lontani tra loro. La conclusione sarà sempre la stessa: la distanza d non cambia com’è indicato nella Fig.1. A questo punto nessuno avrà più dubbi e accetterà la definizione di rette parallele. Per quale motivo ciò che capita in un tratto di decine di chilometri non dovrebbe proseguire oltre, fino all’ultima stazione? In realtà è proprio così e ce lo dimostrano anche i treni che arrivano dall’ultima stazione (facciamone passare almeno uno): se le rette non fossero parallele avrebbe deragliato.

Abbiamo fatto nostro un concetto fondamentale della geometria euclidea (quella che insegnano a scuola e che descrive molto bene i nostri dintorni) e ne siamo contenti. Ma che c’entra con l’infinito? C’entra, c’entra, fidatevi!

Se aveste a disposizione un bel deserto tipo quelli dei film western sarebbe meglio, ma basta la Pianura Padana e anche meno. Mettetevi vicino alla ferrovia e guardate il binario che si allontana . Cosa concludereste senza avere alcun dubbio? “Due rette parallele si incontrano sicuramente”. Si vede benissimo e non bisogna nemmeno avere davanti a sé il deserto del Nevada. Ce lo illustra benissimo la Fig. 2 che è proprio quello che chiunque vedrebbe con i propri occhi. Accidenti. Una delle poche cose che avevamo capito viene immediatamente distrutta dai nostri occhi. Eppure essi sono sempre stati perfetti (o quasi, nel mio caso). L’esperto di turno ci direbbe subito che è solo un’illusione, un qualcosa che ci sembra vero ma che non lo è. Magari parlerebbe anche di prospettiva e di punti di fuga. Non statelo a sentire! Non perché abbia torto, ma perché se lo seguite vi scapperà ancora una volta il concetto di infinito che invece avete davanti a voi a portata di mano.

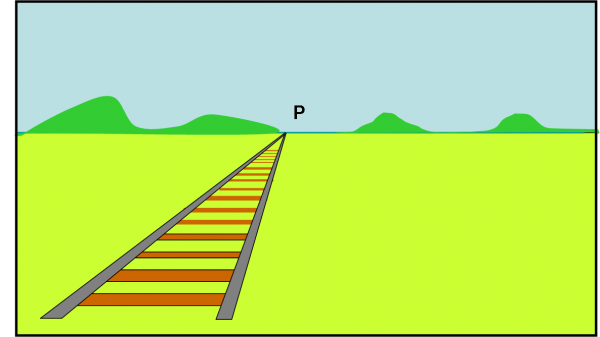
La geometria non se lo fa scappare e ci dice veramente come stanno le cose. Attenzione, allora, a questa frase che diventerà la nostra per potere andare avanti con maggiore sicurezza: “Due rette parallele si incontrano in un solo punto, il punto all’infinito”.

Cosa ci regala questa nuova definizione? Conserva la vecchia definizione delle rette parallele. Infatti, in qualsiasi punto si vada la distanza tra le rotaie rimane sempre costante. E’ ovvio: non le abbiamo misurate nel punto in cui si incontrano. Se, però, guardiamo davanti a noi quel punto così importante continua essere ben visibile e sembra quasi giocare con noi. A mano a mano che ci spostiamo sulla ferrovia sembra allontanarsi sempre di più. Un punto un po’ bizzarro e scherzoso, ma del tutto reale: lo posso vedere benissimo e anche disegnare usando la regola “tecnica” della prospettiva.

Ricapitoliamo brevemente. Attraverso i nostri occhi e utilizzando la geometria più banale siamo riusciti a definire e a vedere un punto che si trova all’infinito. Una grande conquista che né la matematica né la fisica ci permettevano di “toccare” così bene con gli occhi. Attenzione, però, toccare con gli occhi non vuol dire toccare con le mani. Se la ferrovia andasse dalla Terra alla Luna, potremmo seguirla tutta, continuando a fare misure, ma non troveremmo mai quel punto. Eppure prima di partire siamo sicuri di vederlo: è proprio là davanti a noi. E’ un po’ come la pentola d’oro degli arcobaleni. Più ci avviciniamo a lei (ossia alla base dell’arcobaleno) e più si sposta lontano. Insomma, il punto all’infinito è un punto molto speciale che esiste ma è irraggiungibile.

Due amici molto intimi

Ci ritorneremo più in  là, ma fate attenzione che la definizione del punto all’infinito di due rotaie ci permette di comprendere perfettamente anche il concetto dell’amico più intimo dell’infinito: lo zero. Sembrano proprio uno l’opposto dell’altro, ma sono invece strettamente collegati: se esiste uno deve esistere anche l’altro. Utilizzando solo gli occhi, cosa potreste anche dire che succede in quel punto all’infinito delle rotaie? Semplice: “La distanza tra i due binari è uguale esattamente a zero. Ossia, esse si toccano perfettamente in un punto; ma un punto ha, per definizione, dimensioni nulle, come ci hanno insegnato fin dai primi anni di scuola”. Il punto all’infinito ci regala quindi due concetti in uno: quello di infinito e quello di zero. Niente male per davvero.

A questo punto, possiamo anche alzare gli occhi al Cielo e accorgerci che anche lui poteva darci informazioni simili. Due stelle che girano una intorno all’altra si manifestano come due punti che restano sempre alla stessa distanza tra loro (anzi supponiamo per semplicità che siano proprio due punti luminosi e non dei dischetti di un certo dimetro angolare). Tuttavia, se il sistema è vicino, misuriamo una certa distanza identificata dall’angolo che le separa. Se la stella è più lontana quest’angolo diminuisce fino a che le due stelle diventano una sola (sappiamo anche come chiamare quest’angolo: potere separatore dell’occhio o del telescopio). Se potessimo tracciare le linee che rappresentano gli spostamenti apparenti delle due stelle (sempre alla stessa distanza assoluta tra loro) mentre si allontanano da noi, disegneremmo esattamente un paio di rotaie che s’incontrano in un punto all’infinito. Per noi la distanza tra le stelle è diventata zero.

Fermi tutti. Qualcuno potrebbe dirmi: “Quel punto è misurabile facilmente se conosco la vera distanza tra le stelle e il potere separatore del telescopio. Basta applicare una semplice formula di trigonometria piana. Caro Enzo hai raccontato solo bugie… Ho calcolato quel punto e non si trova poi molto lontano. Sicuramente più vicino di moltissime stelle e galassie che esistono nell’Universo. Altro che punto all’infinito!”

Errore! Il potere separatore non definisce un vero punto di dimensione nulle, ma un limite relativo a noi e al nostro strumento. Se si potesse avere un potere risolutore uguale a zero, ossia si potessero spostare le stelle fino a vedere la loro distanza apparente uguale veramente a zero, l’Universo non ci basterebbe. Il punto all’infinito ci porta, quindi, realmente verso un concetto di infinito di tipo fisico. Anche in questo caso, è legato allo zero, dato che la distanza apparente tra le stelle diventerebbe esattamente zero. In realtà, le due stelle sono un esempio non proprio perfetto, perché, per vicine che siano, non potrebbero mai ridursi a un solo punto, dato che hanno delle dimensioni finite. Sarebbe molto meglio prendere due fotoni. Tuttavia, l’importante è il concetto di base e mi sembra sia abbastanza chiaro.

Cosa dobbiamo concludere? Il punto all’infinito esiste ed è visibile, ma è irraggiungibile. Lo possiamo descrivere con la matematica (dato che appartiene alla geometria) e lo possiamo facilmente disegnare (con una qualche geometria proiettiva e/o con la prospettiva), ma non possiamo mai toccarlo fisicamente. Abbiate pazienza, ma non potevamo certo sperare di più. Lo abbiamo definito, l’abbiamo visto, dobbiamo accontentarci. Tuttavia, non lamentiamoci, dato che sarebbe stato ancora più complicato utilizzare i numeri o la fisica. Inoltre, la definizione “intoccabile” del punto all’infinito ci permette di andare ancora oltre.

Costruiamo l’infinito geometrico

Un'altra definizione che tutti conoscono fin dalle elementari è: “Per due punti passa una e una sola retta”. E’ anch’essa sicuramente vera e si può provare in mille modi. Questa definizione ci consente di andare oltre nel nostro modo di rappresentare geometricamente l’infinito. Prendiamo un'altra ferrovia, che non sia parallela a quella di prima. Se infatti fosse parallela prima o poi la vedremmo unirsi all’altra nel loro punto all’infinito, come ci dice la nuova definizione di rette parallele che abbiamo dato poco fa. Questa ovvia conclusione ci dice chiaramente che ogni sistema di rette parallele ha uno e un solo punto all’infinito, come ci mostra molto bene la Fig.3. L’infinito riesce a sintetizzare molto bene le cose, non c’è che dire. Invece di tante rette parallele si può considerare un solo punto.

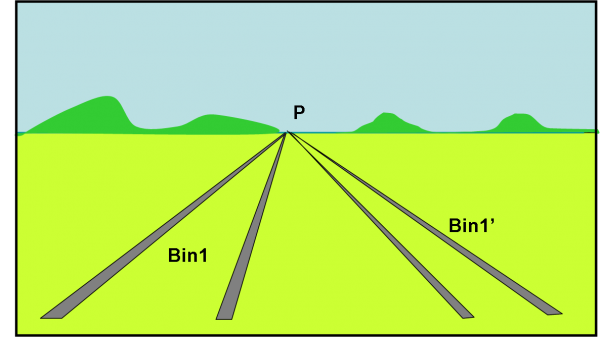
Se la nuova ferrovia non è parallela alla prima, avrà anche’essa un suo punto all’infinito diverso da quello precedente. Disegniamolo in  Fig. 4.

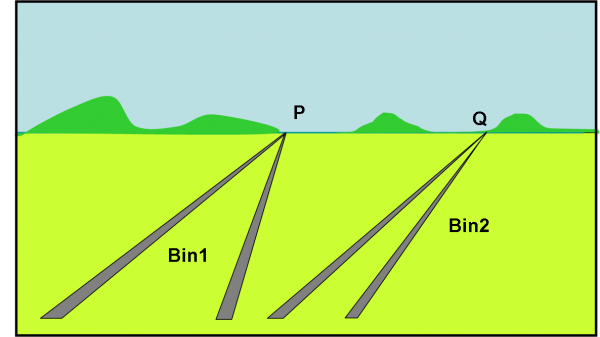
Due punti che, in fondo, poco c’importa che siano entrambi all’infinito: sono comunque due punti ben rappresentabili in una figura e ben visibili con i nostri occhi. Ma, sappiamo che per due punti passa una e una sola retta. Sarà ancora vero per i punti all’infinito? Perché no! Basta tracciare la retta che li unisce. Questa retta prende il nome di retta all’infinito e unisce punti all’infinito, come mostrato in Fig. 5. La cosa sta diventando proprio divertente.

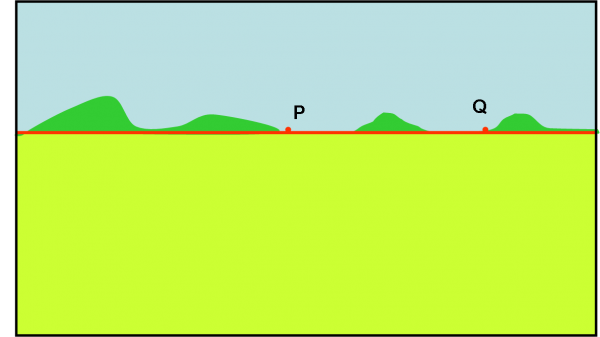
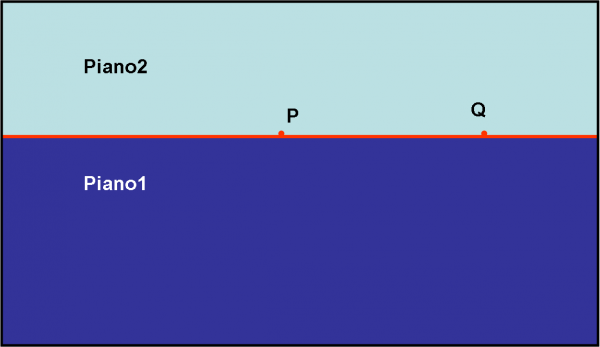
Andiamo a prendere un’altra banale definizione della geometria euclidea. Essa dice: “Una retta qualsiasi può sempre essere individuata dall’intersezione di due piani” o , in altre parole, “due piani non paralleli definiscono una retta attraverso la loro intersezione”.  L’ultima definizione può essere facilmente trasformata in “due piani paralleli hanno una sola linea intersezione, quella all’infinito”. La stessa retta che abbiamo definito attraverso due punti all’infinito. Non abbiamo, infatti, più paura di lavorare con rette o piani paralleli. Facciamo un  semplice esempio. Ai nostri occhi il mare e il cielo sembrano proprio essere due piani paralleli. In realtà la geometria ci permette di trattarli così e quindi di definire la loro retta intersezione che deve stare all’infinito. Questa retta è il classico orizzonte, come mostrato nella Fig. 6. Possiamo quindi dire, analogamente a prima, che tutti i piani paralleli possono essere rappresentati da una sola retta all’infinito.

Ridendo e scherzando abbiamo introdotto punti e rette all’infinito (Attenzione: una retta infinita è tutt’altra cosa. Una retta infinita è qualcosa che non ha un inizio e una fine, ma questo concetto vale per qualsiasi retta). Anche se le cose diventerebbero più complicate per essere disegnate in modo intuitivo è facile estendere il concetto di punti e linee all’infinito, introducendo anche il piano all’infinito. Non è difficile definirlo a parole, ricordando un’altra definizione elementare: “Due rette incidenti o parallele identificano sempre un solo piano”, ma anche “dati tre punti nello spazio esiste uno e un solo piano che li contiene”, o ancora “data una retta e un punto esterna ad essa esiste un solo piano che li contiene”. Basta, allora, dire che dati tre punti all’infinito esiste un piano che li contiene e che prende il nome di piano all’infinito. Esso è l’insieme di tutte le rette e i punti all’infinito definiti precedentemente.

Cari amici, abbiamo ottenuto un’estensione del piano euclideo e lo chiamiamo piano ampliato. In esso, infatti, le definizioni di ciò che capita nellageometria “normale” può trasferirsi senza problemi all’infinito.

ATTENZIONE: se andate a leggere un articolo che ho scritto sull'interno dei buchi neri (QUI), vi accorgerete immediatamente che i concetti spiegati finora (e che sembrano puramente teorici) possono essere applicati immediatamente e fornirci un quadro d'insieme altrimenti impossibile. Ho aggiunto questa frase per rispondere ad Andrea I che mi chiedeva di mostrare appena possibile le applicazioni pratiche della matematica. Contento?

Fermiamoci qui se no le cose si complicherebbero troppo. Non voglio nemmeno dirvi che in questo piano ampliato una retta può essere perpendicolare a se stessa e altre cose piuttosto strane. E’ comunque il posto migliore dove far “vivere” i celebri numeri complessi, guidati dalla ancor più celebre radice quadrata di meno uno e indicata con i. Ma di cose assurde ne abbiamo già tante nella MQ e, per il momento, non pretendiamo troppo. Lo studio del piano ampliato e delle sue caratteristiche fa parte di esami universitari di alto livello e di rappresentazioni grafiche che mi fanno ancora girare la testa se ci penso…

Abbiamo un infinito con cui lavorare

Torniamo a noi e all’infinito. Con i concetti banali e alla portata di tutti che abbiamo introdotto non è adesso difficile passare alla definizione matematica di infinito e di zero. Ciò ci permetterà di introdurre alcune operazioni fondamentali, utilissime nella stessa matematica, ma anche nelle definizioni fondamentali della fisica, quali la velocità, l’accelerazione e cento altre. Proprio quelle che avevo cercato di descrivere con molta più fatica nel libro “la Fisica addormentata nel Bosco”. Saremo così in grado di studiare una funzione matematica, senza preoccuparci se ci sono punti che sembrano “intoccabili”. Il piano ampliato ci ha fornito la possibilità di maneggiarli senza problemi.

Prima di lasciarci, fatemi riportare i simboli che si usano per definire, in matematica, lo zero e l’infinito. Vi sembrerà un’aggiunta veramente stupida. Può darsi, ma è meglio richiamarli, dato che la prossima volta inizieremo a fare le operazioni più banali proprio con questi strani numeri.

Zero  --> 0

Infinito  --> ∞

QUI il capitolo successivo

QUI l'intero corso di matematica