2. Zero e Infinito si incontrano e si sommano *
Abbiamo introdotto i concetti geometrici di zero e infinito. Possiamo ora trasportarli lentamente nel mondo della matematica attraverso le operazioni più semplici che essi possono eseguire tra di loro e con numeri qualsiasi. Insomma, facciamoli entrare nel mondo di tutti i giorni.
Dopo aver introdotto il concetto geometrico di zero e infinito, non ci sembra più tanto impossibile utilizzarli nelle più semplici operazioni di matematica. Basta tenere sempre presente la loro essenza. Facciamo, allora, una breve sintesi “matematica” di quanto capito geometricamente.
Cos’è lo zero? Bene, è la distanza tra le rotaie quando entriamo nel piano ampliato. Ossia, è la distanza apparente tra loro nel punto all’infinito. In altra parole, più si guarda lontano verso il punto all’infinito e più la distanza tra le rotaie diminuisce. Molto semplicemente potremmo dire che zero è l’inverso di infinito (e viceversa). Tuttavia, possiamo esprimere questa conclusione in un modo più “ferroviario”… Continuiamo a ragionare con le rotaie e diciamo la seguente frase: “Se il binario raggiunge il punto all’infinito, la distanza delle rotaie deve diventare zero, ossia convergere verso il punto all’infinito del binario”. Come possiamo tradurre questa frase estremamente intuitiva, ma troppo lunga per portarcela sempre dietro? Vogliamo provare a scriverla in modo matematico. Che ne dite di questa espressione?
d = D/r
Cosa vuol dire. Beh… d è la distanza apparente tra le rotaie, D è la distanza vera tra le rotaie e r è la lunghezza delle rotaie. D è una costante, dato che è quella che è e non può cambiare. Espressa in millimetri, centimetri o metri, poco importa. Possiamo considerarla un numero, come 1, 2 oppure 57. Ovviamente, per adesso non può essere zero dato che in quel caso non esisterebbe il binario, ma una sola rotaia! Possiamo, quindi, usare un’unità di misura a piacere e assegnarle il valore uguale a 1 (sia quel che sia, metri, piedi, pollici, indici, mignoli o quello che preferite). Analogamente la distanza r non può essere zero perché, anche in questo caso, non esisterebbe la rotaia (una rotaia di lunghezza zero non esiste per definizione).
Per tutti gli altri valori, invece, la relazione può essere utilizzata, anche se -voglio ribadirlo- è solo una nostra soluzione empirica che farebbe rabbrividire qualsiasi matematico. Pazienza, prima o poi correremo ai ripari. Per adesso sfruttiamola dato che ci serve a definire la relazione che intercorre tra zero e infinito. Quando faremo nostri alcuni concetti più difficili, la sistemeremo meglio. Per adesso, accontentiamoci. Di sicuro ci dice una cosa perfettamente logica: aumentando la lunghezza del binario r, diminuisce la distanza apparente d tra le due rotaie.
Non stiamo nemmeno a perdere tempo nel calcolare quanto vale d per diversi valori di r. Basta riportare la Fig. 7 dove ho segnato le varie grandezze sulla rotaia che si stringe.
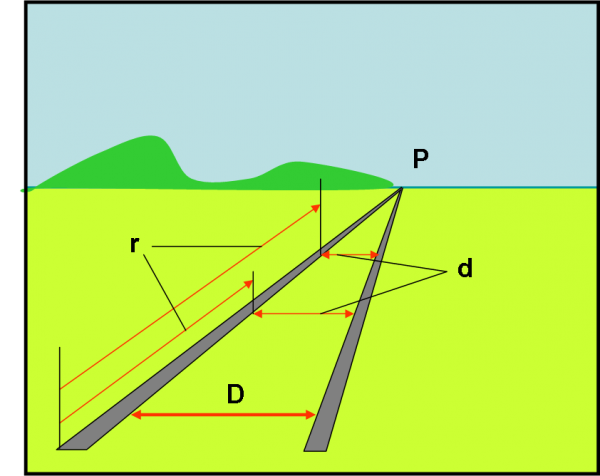
I più smaliziati saprebbero benissimo riconoscere triangoli simili e/o funzioni trigonometriche e/o altro ancora (ad esempio la parallasse trigonometrica), ma non occupiamocene, per adesso almeno. Andiamo direttamente alla “fine” della rotaia. Sappiamo benissimo quanto vale la distanza nel piano ampliato, ossia quando arriviamo alla retta dell’orizzonte. La distanza è proprio infinita, nel senso geometrico che le abbiamo dato la volta scorsa. Sappiamo, però, anche che raggiunto il punto all’infinito della rotaia, la loro distanza d diventa zero (è un punto senza dimensioni). Non stiamo facendo altro che applicare il concetto stesso di punto all’infinito, sia per la lunghezza del binario che per la sua larghezza. Cosa diventa la nostra banale formula scritta precedentemente? Banale:
0 = 1/∞
Come, in fondo, già prevedevamo: lo zero è l’inverso dell’infinito. Vale quindi anche:
∞ = 1/0
No, non spaventatevi, abbiamo trattato zero e infinito come numeri qualsiasi. Infatti, non vi stupireste senz’altro se scrivessi: 5 = 10/2 e poi la trasformassi in 2 = 10/5. Bene, ho fatto lo stesso con i simboli introdotti la volta scorsa, per non portarci sempre dietro una lunga tiritera di parole.
Notate bene che se anche avessi definito la distanza D con altre unità di misura e avessi trovato per lei valori numerici diversi, tipo 2, 5, 75 , ecc. La relazione non sarebbe cambiata di molto:
0 = 75/∞
e analogamente
∞ = 75/0.
D’altra parte sappiamo bene che qualsiasi sia la distanza tra i binari, essi devono incontrarsi all’infinito sempre in un punto di dimensioni uguali a zero. Questa frase vuole anche dire: “Tutte le rette parallele tra loro si incontrano in un solo punto all’infinito”. Frase che avevamo già utilizzato la volta scorsa.
Si può anche ragionare più terra-terra. Come si fa a confrontare un numero, per grande che sia, con –nientemeno- che infinito, il massimo dei massimi? E’ ovvio che rispetto a infinito qualsiasi numero è ben poca cosa. Essere 1 oppure 10 oppure 10000 non cambia la questione. E’ come mettere su una bilancia un pallina da tennis da un lato e un pianeta dall’altro. Analogo ragionamento si può fare per lo zero. Qualsiasi numero, per piccolo che sia, è enorme rispetto allo zero. Ne segue che paragonare un numero con il minimo dei minimi non può che far pendere la bilancia verso il numero.
Dire che qualsiasi numero (diverso da zero e da infinito) diviso per zero dà infinito o –analogamente- che qualsiasi numero diviso per infinito dà zero sembra una banalissima conseguenza, ma teniamola bene a mente perché tra non molto ci servirà per risolvere un grande dubbio. Ripetiamola ancora:
Qualsiasi numero diviso per infinito dà zero e qualsiasi numero diviso per zero dà infinito
Il “qualsiasi numero”, però, deve essere, per adesso almeno, diverso da zero e da infinito. E’ abbastanza comprensibile, ma tra non molto capiremo meglio il perché…
Possiamo anche riflettere su un altro punto fondamentale: il concetto di infinito è strettamente legato a quello di zero. Sono due grandezze indivisibili: sotto particolari condizioni (piano all’infinito) se esiste una deve esistere anche l’altra. Anzi, dove se ne incontra una si deve incontrare anche l’altra. Questa frase puramente geometrica si trasforma nella relazione appena trovata, ossia 1/0 = ∞ o 1/∞ = 0 . L’infinito conduce allo zero e lo zero conduce all’infinito
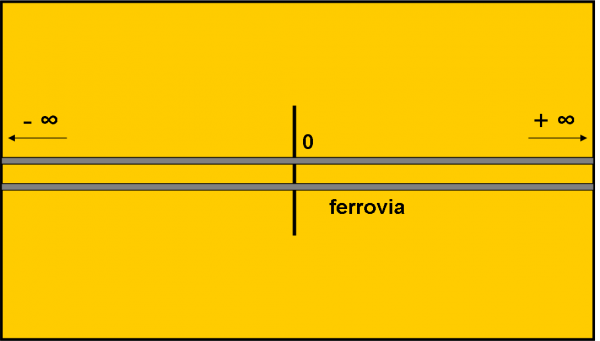
A questo punto è meglio completare la definizione di infinito. Se noi ci troviamo nel bel mezzo di un deserto, dove passa una ferrovia, vedremo un punto all’infinito dei binari sia da un lato che dall’altro. Non sono certo uguali! Definiamo allora un verso positivo e uno negativo alla ferrovia, come riportato in Fig. 8. Da un lato avremo l’infinito positivo e dall’altro quello negativo. Nello stesso identico modo in cui diamo il valore + 5 o - 5 a un numero rispetto allo zero. Per lo zero (al momento) non ci sono problemi: + 0 e – 0 sono la stessa cosa.
Vogliamo provare a scrivere le altre possibili relazioni tra zero e infinito oppure tra essi stessi? Non ci dovrebbero essere problemi. Al limite, ciò che non riusciamo a definire lo identificheremo come indeterminato. Vedrete quanto sarà importante questa parola.
Cominciamo con le due più semplici: l’addizione e la sottrazione. Esse sono in realtà la stessa cosa se consideriamo i numeri negativi, dato che la differenza di due numeri positivi è la somma di un numero positivo e di uno negativo.
Bene possiamo scrivere un bel po’ di possibili operazioni
0 + 0
0 - 0
∞ + ∞
∞ - ∞
∞ + 0
∞ - 0
0 - ∞
Potreste facilmente trovare il risultato da soli. Permettetemi, però, di essere proprio come un professore esageratamente meticoloso (di matematica appunto) e di spiegare tutti i passaggi anche quelli apparentemente più facili.
0 + 0 vuol dire sommare niente a niente. E’ ovvio che niente più niente rimane comunque niente, ossia il risultato non può che essere 0.
0 – 0 non cambia di molto la situazione. Togliere niente a niente è sempre niente. Il risultato è nuovamente 0.
∞ + ∞ vuol dire aggiungere all’infinito un altro infinito. Beh… non esageriamo! Oltre all’infinito non ci può essere che infinito, se no che infinito sarebbe? Possiamo concludere tranquillamente che il risultato è ancora ∞.
∞ - ∞ vuol dire togliere infinito all’infinito. Verrebbe ovvio dire che il risultato è zero, come 5 – 5. Purtroppo, non possiamo esagerare con la somiglianza dell’infinito a un numero reale e ben determinato. Come visto precedentemente, l’infinito non è veramente quantificabile. Proviamo a metterla così (state attenti perché più in là questo ragionamento sarà essenziale): ci sono due ferrovie che vanno entrambe all’infinito, ma in una delle due il treno va più veloce. Cosa potremmo concludere? Che il treno più veloce raggiunge l’infinito prima del secondo? Sì, lo so, sembra un discorso assurdo, ma vedremo che è un concetto fondamentale.
Non perdiamo troppo tempo e ammettiamo, per adesso, che l’infinito non è qualcosa di realmente misurabile. Va tutto bene finché lo si paragona a zero o un altro numero qualsiasi, ma quando si tratta di sottrarre due infiniti la risposta non è ovvia e non ne siamo capaci (per adesso, ovviamente). Insomma, per concludere, la sottrazione di due infiniti non ha un risultato immediato. Devo studiarli più da vicino e non posso concludere che la differenza sia zero. In altre parole, la soluzione è indeterminata. E’ il primo caso che troviamo. Teniamolo bene a mente.
∞ + 0 e ∞ - 0 non danno problemi, anche per quanto abbiamo detto precedentemente. Togliere niente o aggiungere niente a un qualsiasi “tipo” di infinito non può cambiare assolutamente il concetto di infinito. Il risultato è sempre ∞ in entrambi i casi.
0 - ∞ è praticamente la stessa cosa, ma il risultato ci dà l’infinito della parte opposta del binario, ossia - ∞.
Riscriviamo la lista di prima con i risultati a fianco. Scusate la lungaggine, ma è meglio partire con il piede giusto. Fidatevi…
0 + 0 = 0
0 – 0 = 0
∞ + ∞ = ∞
∞ - ∞ = indeterminato
∞ + 0 = ∞
∞ - 0 = ∞
0 - ∞ = - ∞
Per fare un buon lavoro, dovremmo dire qualcosa anche riguardo alla situazione in cui si sostituisse il numero zero con un numero qualsiasi n. In parte ne abbiamo già discusso, ma vale la pena ribadire i risultati. I più esperti saltino pure questo nuovo banalissimo elenco.
n + 0 = n
n – 0 = n
∞ + n = ∞
∞ - n = ∞
n - ∞ = -∞
Cosa ci confermano queste relazioni? Ciò che già sapevamo: lo zero non cambia il valore di un numero, sia che si aggiunga o si tolga. Inoltre, aggiungere o togliere un numero finito all’infinito non cambia assolutamente il suo valore di infinito. Solo un altro infinito può metterlo in crisi.
Sarò sicuramente pedante e lento, ma ritengo giusto fermarmi qui. Per adesso tenetevi ben stretti due risultati fondamentali:
1) Dividere un numero qualsiasi (diverso da zero) per zero dà sempre infinito così come dividere il numero (diverso da infinito) per infinito dà sempre zero.
2) Sottrarre infinito da infinito è un’operazione che, per il momento, non ci fornisce un risultato concreto, ossia la soluzione è indeterminata.
Come abbiamo visto, il punto (2) comincia a crearci problemi. Forse, le operazioni che conosciamo non funzionano sempre bene nel piano ampliato. Vedremo presto come vanno le cose con le altre operazioni…
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






36 commenti
Splendido Enzo, grazie!....L'unica cosa che mi lascia un po' perplesso é il -∞. Dare un "verso" all'infinito mi mette in difficoltá in termini di logica.
caro Andrea,per capire meglio il significato del "verso", pensala così:
Scegliamo un verso sulla ferrovia: i treni che viaggiano a destra vanno in verso positivo e quelli che vanno a sinistra vanno in verso negativo. Una nostra scelta, ma l'importante è che si sappia bene e che la usino tutti.
A questo punto, potremo dire che il primo treno va verso l'infinito (dove s'incontrano le rotaie) in verso positivo e quindi il punto infinito lo chiamiamo infinito più. Viceversa per l'altro treno. Cambia solo il segno, che sta a indicare solo da che parte viaggia il treno... Questa visione è utile perchè ci porta direttamente al concetto di limite... e ci fa capire cosa vuol dire tendere a infinito più o a infinito meno. Nient'altro che dirigersi verso infinito in un verso o nell'altro.
La stessa cosa si applica anche a un punto che non sia infinito... ma mi fai correre un po' troppo. Non preoccuparti tanto ci ritorneremo presto.
Ok per l'infinito "normale" ma
- i numeri sono infiniti;
- numeri pari sono infiniti, e sono la metà dei numeri
- i numeri dispari sono infiniti e sono la metà dei numeri
- i numeri primi sono infiniti ma sono tutti ,tranne il 2, dispari e NON sono TUTTI i numeri dispari
e ciò vale per in numeri quadrati, cubi etc.
Non ho mai capito Cantor se me lo puoi spiegare GRAZIE
C'é quindi bisogno di partire sempre da un punto soggettivo, da considerare come il punto 0 (cioé il punto in cui la misurazione esprime lo 0). É proprio quello che mi ha lasciato un po' perplesso. Probabilmente perché confondo il concetto di infinito con il tendere all'infinito. Grazie per le delucidazioni Enzo
caro Walter,
non capisco bene cosa intendi quando dici che i n umeri sono infiniti e cose del genere. Non sono certo in contrasto con i concetti esposti negli articoli. I numeri non fanno altro che definire le posizioni lungo le rotaie: se le misuri pezzo a pezzo puoi ottenere solo i numeri interi. Se vai più nel sottile anche i frazionari e via dicendo. Non ha nemmeno tanto senso dire che i numeri positivi sono tanti come i numeri negativi (almeno da un punto di vista concettuale), essendo entrambi infiniti.
Diverso è il discorso su Cantor e i suoi insiemi transfiniti e relativi numeri. Lì si entra proprio nella matematica più profonda. Non posso certo spiegarlo in poche righe, ma lo tengo in conto per un articolo dedicato, sperando di rendere comprensibili certi concetti che hanno bisogno di conoscenze profonde sulla teoria degli insiemi... Ci studierò sopra...
Tieni anche conto che Cantor fu considerato pazzo o poco meno (fu anche spesso ricoverato) e legò le sue teorie anche a Dio e all'assoluto. Tuttavia, la sua matematica estrema ha dato il via alla teoria degli insiemi, oggi riconosciuta valida da tutti. Insomma, non è cosa facile...
caro Andrea,
tutta la geometria ha bisogno di partire da punti prestabiliti, dando direzioni e verso. Lo fanno le coordinate cartesiane che ti permettono di definire ogni punto nel piano o nello spazio. L'importante è che la scelta dei punti non cambino i risultati. E', in fondo, il concetto di sistema di riferimento. Loro si possono anche cambiare, ma le leggi fisiche non lo fanno, sempre che si possa passare da uno all'altro mediante certe trasformazioni come la traslazione e la rotazione solidale. Se poi, invece, ne facciamo accelerare uno, allora cadiamo nella teoria della relatività... ma questo è un altro discorso.
Teniamo presente che stiamo iniziando l'analisi matematica elementare e non possiamo pretendere di arrivare subito alle teorie fisiche più estreme... Ogni cosa a suo tempo, senza cercare di voler vedere troppo avanti
Ciao ragazzi.
Mi è venuto un dubbio concettuale quando replichi: "Nient’altro che dirigersi verso infinito in un verso o nell’altro."
Ci riferiamo allo stesso infinito ma muovendoci in due direzioni opposte?
Oppure più semplicemente, visto che sia i numeri negativi che quelli positivi sono infiniti, stiamo parlando di due insiemi infiniti separati?
Ciao.
Andrea
Probabilmente (certamente) mi sono espresso male.
Non intendevo riferirmi all'esempio delle rotaie ma all'infinito come concetto matematico.
Ciò che intendevo e che la somma
dei numeri pari, che sono infiniti, e dei numeri dispari, che sono infiniti da un infinito che dovrebbe esser "maggiore" al loro rispettivo infinito.
Vero, la considerazione sul sistema di riferimento e alla relativitá mi é saltata subito in mente......questo é decisamente un gioco divertente ed emozionante
@Andrea.Andrea
nel senso che vogliamo dare a queste "lezioni" dobbiamo limitarci a pensare all'infinito come uno solo. Tuttavia, come avevamo detto nel primo articolo, esiste un piano all'infinito, composto da vari punti (ognuno determinato da una coppia di rette parallele, ricordi?). Sulla base delle condizioni di partenza (il punto origine in cui siamo noi) possiamo dividere i due punti all'infinito della rotaia in uno positivo e uno negativo, sulla base del verso che ho scelto. Tutto lì. Cerchiamo di non confondere il significato geometrico di punto all'infinito (che ci è servito per poterlo in qualche modo "vedere" (e capiremo dopo il perchè)) con quello che gli si dà in matematica, ossia l'insieme di tutti numeri. Nel contesto della rotaia, potremmo dire che l'infinito positivo è l'insieme di tutte le traversine a sinistra, mentre l'infinito positivo e l'insieme di tutte le traversine a destra. In entrambi i casi, sono le traversine necessarie per arrivare fino ai due punti all'infinito. Sia che usiamo traversine lontane tra loro, sia che siano molto più vicine, il loro numero prima di arrivare al punto all'infinito sarà sempre infinito.
Consideriamo, quindi, per il discorso che ci interessa, il segno + o - che diamo all'infinito solo un qualcosa che ci indica la direzione per arrivare al piano all'infinito.
Spero di non chiedervi troppo... . Comunque insistete a chiedere, magari riesco a girare le cose in modo ancora più intuitivo...
. Comunque insistete a chiedere, magari riesco a girare le cose in modo ancora più intuitivo...
@Walter,
il tuo discorso cade proprio a fagiolo. Infatti tu stai parlando di insiemi di numeri infiniti e quindi si entra in un campo diverso e più complesso. Per discutere di loro bisognerebbe parlare di geometria superiore (tre), mentre noi stiamo parlando in termini di geometria uno.
In questo contesto, come abbiamo scritto nell'articolo, infinito più infinito dà infinito e non ci interessa se hanno ordini diversi. Per noi, infatti, l'infinito è uno solo (a parte il segno che ci indica solo da che parte si trova). Lo vedremo meglio nel prodotto: dove infinito per infinito NON fa infinito al quadrato!
Compreso Enzo e mi meraviglio di avercela fatta, grazie.
io ne ero sicuro!!!
"non dico sette ma settanta volte sette" (MT 18,22)
anche il concetto di numero grande subisce l'inflazione...
ed i romani non avevano il simbolo per lo zero...
Se scrivo: 1/∞= 0 allora 0*∞= 1 ?
e no, caro mio!!!
le cose sono più complicate... 0*inf = 0/0 =?
alla prossima volta....
caro Beppe, se rileggi l'articolo vedi che ho scritto che qualsiasi numero diviso zero è uguale a infinito, tranne zero e infinito. La rotaia non può annullarsi se no che rotaia è??? e nemmeno avere ampiezza infinita....
0*∞ = 0 a rigor di logica(sempre secondo me)
1/∞ = ∞ sempre secondo me!
Ci ho preso?
caro Andrea... mi dispiace, ma 1/inf. = 0. E' scritto anche nell'articolo....
Ops, me tapino....evidentemente lo devo rileggere con piú attenzione
anche perché la cosa mi incuriosisce parecchio, se non altro per capire dove ho sbagliato nel ragionamento che mi ha fatto scrivere quello che ho scritto.
Grazie Enzo.
Vincenzo sei un grande
Ma dai!! me la potevi concedere la battuta!!
Scusate Enzo e gli altri se dico una sciocchezza ma vorrei provare a vedere se ci si arriva con il ragionamento pur essendo molto lacunoso in matematica:
Geometricamente l'infinito si deve interpretare come il punto all'infinito, quello che però non si raggiunge mai. Lo stesso concetto si applica allo zero, quindi non si raggiunge mai ma si TENDE SOLAMENTE a zero o a infinito.
Matematicamente l'infinito non è quantificabile, anche in questo caso non si raggiunge mai e quindi mi verrebbe naturale considerarlo come un insieme di tantissimi elementi il cui numero non è quantificabile e quindi numerabile.
Lo 0 idem, è paragonabile a dire nulla ed è sempre nel nostro futuro (o passato), il nulla è quindi qualcosa di talmente piccolo da essere non determinabile e quindi non numerabile.
Alla fine ottengo che sia zero che infinito sono non numerabili, conseguentemente la loro multiplicazione o divisione porta sempre un risultato non determinabile o non numerabile.
∞*0 si tradurrebbe, ad esempio, a moltiplicare un numero elevatissimo ma non quantificabile per un numero piccolissimo e non quantificabile.
Vince l'infinitamente grande o l'infinitamente piccolo? nessuno lo può dire.....
@Alexander, spero che ne tu ne Enzo ve ne abbiate se provo a risponderti io.
Per semplicità stringiamo il campo ai soli numeri naturali, cioè i numeri 1, 2, 3 ecc. che sono un sottoinsieme dei numeri reali. Il più immediato, come contare con le dita o enumerare degli oggetti. Lo zero rappresenta la mancanza degli oggetti. E' quindi ben tangibile, se prima ho due caramelle e le mangio tutte due, dopo avrò 0 caramelle (e se non me li lavo, i denti cariati). L'infinito invece è un po' più tosto, per semplicità è il numero più grande che ci può venire in mente, ma... a cui si può aggiungere sempre almeno una unità, quindi non avrà mai fine. E' per questo che i filosofi ed i matematici hanno deciso di indicare con il simbolo ∞ questa quantità non enumerabile...
scusa Beppe... pensavo in realtà che fosse solo una battuta... ma temevo che senza dire niente qualcuno avrebbe potuto fare confusione. Con le moltiplicazioni le cose si complicheranno e quindi ho preferito essere "drastico". Spero che mi capirai...
caro Alexander,
direi che sei stato quasi perfetto!!!! Siamo di fronte ai concetti di infinito e di infinitesimo. In entrambi i casi è sempre possibile trovare un numero piccolo a piacere o grande a piacere che sia più vicino a zero o a infinito di quello che consideri (lo diremo in modo molto più esatto quando parleremo di limiti). Considera anche che il vero problema è in realtà infinito (non quantificabile) e che lo zero può essere scritto come 1/inf. Qunado hai 0*inf è come se avessi inf/inf e quindi.... ????? boh????
Ridendo e scherzando stiamo già parlando della prossima lezione. In fondo ne sono contento perché vedo che state usando il ragionamento per andare avanti e non aspettate nuove formulette. Proprio quello che ci vuole in matematica....
Dai ragazzi (per quelli che ancora non le sanno) tra pochi mesi "mangeremo" le derivate come fossero noccioline. Tra poche settimane, invece, sapremo STUDIARE quai tutte le funzioni matematiche e allora vedremo come sono importanti le rappresentazioni grafiche per descrivere le osservazioni...
Bene, moltoooo bene
@ Enzo: hai fatto benissimo! mi sono lasciato trasportare, ti chiedo scusa
A me personalmente fanno impazzire le serie convergenti, credo che in qualche modo siano attinenti.. (fa anche rima!)
ok ci sono, ma in base al ragionamento fatto allora non è correttissimo neanche dire che è zero il risultato di 1/inf. infatti se infinito è un numero non quantificabile perchè in ogni caso posso trovare un numero piu grande del precedente che si avvicina di piu all'infinito (che è sempre nel futuro), allora anche il risultato finale della divisione deve essere una TENDENZA allo zero (valore che è sempre nel futuro).
Ma lo zero assoluto non lo raggiungero' mai come non raggiungero' mai l'infinito assoluto.
E' possibile che si parli di limiti in questo caso?
caro Alexander,
hai centrato il problema. Noi abbiamo voluto trattare infinito come fosse un numero o -meglio- un punto come tutti gli altri. Ci è servito molto per capire come lo si può immaginare e rappresentare concettualmente. Tuttavia, è un qualcosa di irraggiungibile e quindi vale il discorso del "tendere", ossia di avvicinarsi sempre più, ma mai raggiungerlo veramente. Lo zero, ha invece un vantaggio, dato che si può rappresentare molto meglio: un punto senza dimensione (non è facilissimo, ma è più intuitivo).
Ragioniamo così: cominciamo a dividere un numero qualsiasi (prendiamo anche 1) per un numero grandissimo. Il risultato diventa piccolissimo. E più il numero è grande e più il risultato è piccolo. Qualcosa che diventa sempre più piccolo è proprio lo zero. Così come qualcosa che diventa sempre più grande è proprio l'infinito. Benché non ci si possa mai arrivare, possiamo però concludere SIMBOLICAMENTE che 1/inf sia proprio zero. Esso è, quindi, un risultato determinato e non dubbio o impreciso, come infinito meno infinito. Idem per 1/0. Se al posto di zero mettiamo un numero piccolissimo, il risultato è grandissimo, ossia si avvicina sempre di più al concetto di infinito. Se riuscissimo a giungere proprio a zero è allora giusto dire che otterremmo proprio il risultato di infinito. Anche se 0 sembra perfettamente determinato nella nostra visione, ha lo stesso problema di infinito: sfido chiunque a disegnare un punto di dimensioni veramente nulle!
Comunque, sono molto contento. Stiamo arrivando naturalmente al concetto di "tendere a", un concetto che sembra ovvio, ma che va compreso a fondo. Direi che la nostra rotaia ci è servita abbastanza bene.
Sei a posto Alexander... il tuo bagaglio è quello giusto per andare avanti e vedrai che il futuro di darà conferme di ciò che stai immaginando.
Caro Enzo, volevo farti una domanda che so benissimo non ha senso porre (perchè credo dipenda dalla mia (nostra?) incapacità incapcaità di comprendere realmente l'infinito), ma poichè la mia testa ha la stessa capacità matematica della sedia su cui sono seduto mentre scrivo, non riesco a liberarmi di questo problema e vorrei che mi aiutassi a farlo. Abbiamo detto che la distanza tra le rotaie diventa zero solo nel punto all'infinito. In ogni punto diverso dell'infinito la distanza è costante, quindi sempre la stessa. Però sappiamo anche che 0 è sempre più piccolo della distanza delle rotaie (distanza rotaie = a zero è come spieghi una sola rotaia). Però per incontrarsi le rotaie dovrebbero ad un certo punto avvicinarsi e quindi, prima dell'infinito la distanza tra esse dovrebbe ridursi e non "può" quindi essere sempre costante in ogni punto diverso da infinito.....come si fa?
PS dovresti aggiungere un emoticon con il fumo che esce dalla testa
caro Alessandro,
l'esempio delle rotaie va considerato solo come "apparenza". Ossia, ciò che appare dobbiamo considerarlo reale. In tal modo possiamo dare un valore "pratico" a infinito e zero. Lo scopo è solo quello e non possiamo muoverci lungo la rotaia se no rovineremmo il concetto o al limite lo ritarderemmo.
Apparentemente, due linee parallele si incontrano e apparentemente la distanza tra due rotaie non è mai costante, ma continua a diminuire "guardando" (non ANDANDO) più distante. Altra cosa è invece avvicinare le rotaie nel punto in cui sono presente: quello vuol dire ridurre le rotaie a una sola, come dici tu.
Immagina di apparire dal nulla nel mondo e guardare una ferrovia (senza poterti muovere) per la prima volta. Cosa diresti se ti domandassero cosa sono e come si comportano le due rotaie? Tu diresti che si avvicinano sempre più e che si incontrano in un punto lontano lontano. Questo è quello che ci serve per definire l'infinito in modo geometrico... rendere reale l'apparenza prospettica.
Non fumare troppo che il fumo fa male!!!!
nonostante la spiegazione non riesco a capire perchè ∞ – ∞ non fa zero ed invece è indeterminato.
Quindi si deve supporre che l'infinito non è sempre uguale ossia che ci sono infiniti diversi?
caro Carlo,
questa prima parte ci serve solo per prendere un po' di dimestichezza con il concetto di infinito in geometria e matematica. Le operazioni le ho usate per dimostrare che in realtà non sono grandezze facilmente quantificabili e che quindi vanno trattate con le molle. Alcuni risultati sono ovvi, altri molto meno e non veramente definibili. Come dici tu, infinito è qualcosa di vago e quindi mentre si è sicuri che è più grande di qualsiasi numero e che quindi sommarglielo oppure toglierlo non cambia niente, non è altrettanto quantificabile il significato di togliere infinito a infinito, proprio perché uno può essere raggiunto prima di un altro. Ma questo lo potremo vedere solo più avanti... Possiamo anche ammettere, in un certo verso, che non tutti gli infiniti sono uguali... ma senza esagerare troppo. Vedrai che ci torneremo sopra in modo più controllabile...
Se a scuola mi avessero spiegato in questo modo la "tendenza a 0 o a ± ∞" avrei capito i limiti molto più in fretta. Bravissimo, grazie
grazie Givi! . Mi fa un enorme piacere che tu sia già arrivato alla conclusione con pochi accenni...
. Mi fa un enorme piacere che tu sia già arrivato alla conclusione con pochi accenni... 
Ma ancora devo veramente a cominciare a spiegare i limiti
Seconda lezione, seconda domanda (ormai voglio recuperarmi tutto il corso :-D): c'è una dimostrazione per la formula che enunci all'inizio, cioè D/r=d?
caro Stefano,
come si dice nel testo è solo una relazione empirica che ci dice che al crescere di r, d diventa sempre piccola... tutto lì... ci serve solo per mostrare il legame tra zero e infinito...
poco sotto c'è scritto:
"è solo una nostra soluzione empirica che farebbe rabbrividire qualsiasi matematico."
Grazie mille per le risposte!