Abbiamo già parlato delle più semplici funzioni trigonometriche. Sia perché ci sono servite per definire il coefficiente angolare di una retta, sia perché attraverso di loro si può passare da un sistema di coordinate cartesiane a uno di coordinate polari (e viceversa). L’uso delle funzioni trigonometriche permette, in genere, di calcolare facilmente le componenti di un segmento qualsiasi rispetto ai due assi cartesiani. E mille cose ancora… Tuttavia, restano comunque delle funzioni ed è giusto studiarle come abbiamo fatto per le coniche, le rette, il logaritmo e cose del genere.

Possiamo, perciò, vedere anch’esse come “macchine” capaci di lavorare sopra una variabile e trasformarla in un’altra. Cosa fa, ad esempio, la funzione seno? Beh, prende un certo angolo (espresso in gradi o in radianti) e ne calcola  il seno, ossia quel segmento che abbiamo definito nel cerchio trigonometrico. Ovviamente, a ogni angolo corrisponde uno e uno solo seno . Situazione analoga capita alla funzione coseno e alla funzione tangente. Riportiamo nuovamente il cerchio trigonometrico in Fig. 66 e analizziamolo da ogni parte e non solo nella zona positiva delle x e delle y. Impareremo molte cose e molte interazioni tra le funzioni trigonometriche.

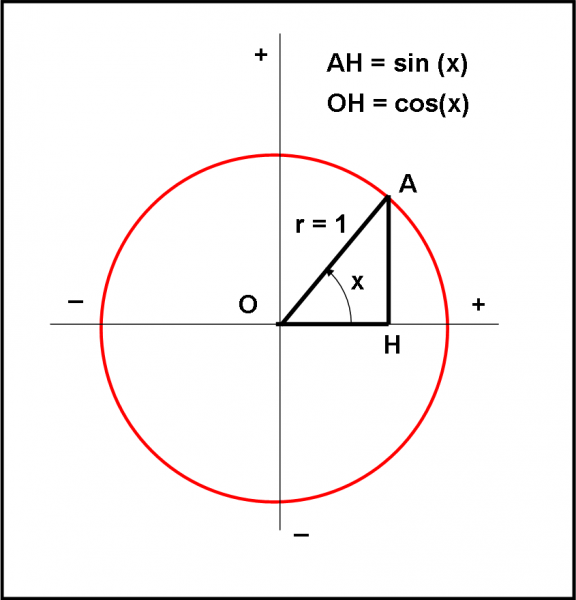
Scriviamo le prime due funzioni e iniziamo a studiarle in dettaglio con l’aiuto della figura precedente.

y = sin(x)

y = cos(x)

Ripeto ancora che il significato è sempre lo stesso: prendi una x (che sia un angolo cambia poco, anche perché potremo sempre usare i radianti che sono numeri…) ed esegui l’operazione trigonometrica corrispondente. In tal modo ottieni la y. Procedimento del tutto analogo a quanto fatto per una retta, dove inserivamo una x, la moltiplicavamo e l’addizionavamo a qualcosa e ottenevamo la y. Scusate se sono un po’ ripetitivo, ma vorrei che la trigonometria fosse intesa per quella che è: un grande aiuto, una medicina spesso unica e non certo una complicazione in più.

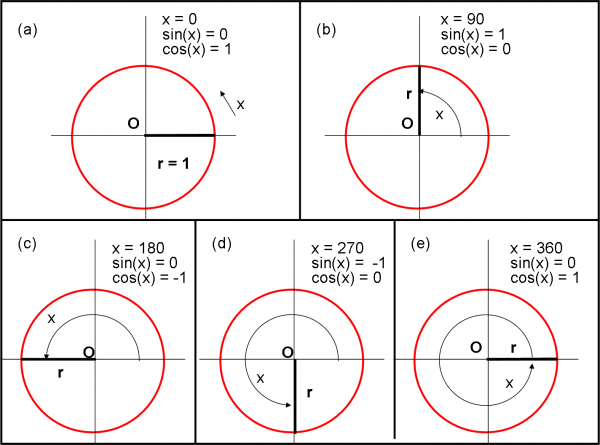
Cominciamo a descrivere nel piano x,y la funzione seno, seguendo il cerchio trigonometrico della Fig. 67(a,b,c,d,e) e la rappresentazione cartesiana della Fig. 68 (curva blu).

In quest’ultima figura, ripeto ancora, la x è un angolo (espresso in gradi o in radianti), mentre la y continua a essere una coordinata lineare.

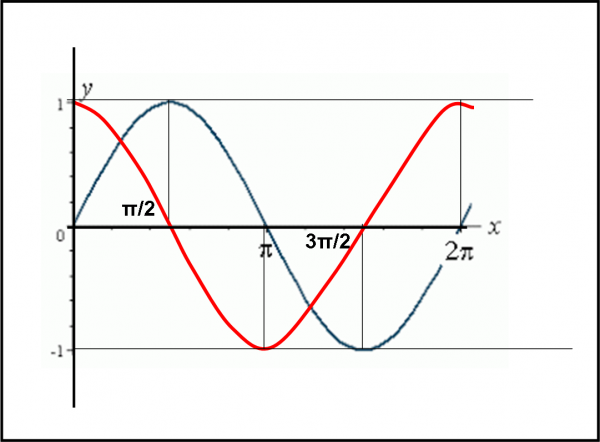
Cosa succede alla funzione seno facendo girare l’angolo x ? Beh, se ruota l’angolo, ruota anche il raggio r (unitario) che ci permette di determinare il seno dell’angolo, attraverso la perpendicolare tracciata dal punto sulla circonferenza fino all’asse orizzontale. Prima di calcolare il valore del seno, possiamo già trarre una conclusione molto semplice e immediata. La funzione DEVE essere periodica, ossia deve ripetersi ogni volta che l’angolo ha compito un  giro completo (360° o 2π).

E’ ovvio, infatti, che 362°, ossia 360° + 2°, dia lo stesso risultato ottenuto per 2°. Il periodo della funzione è quindi di 360° o -se preferite - di 2π. Basta, perciò, studiare la funzione seno tra x = 0 e x = 2π. Prima e dopo non fa che ripetersi. Attenzione: non è che non esista, ma solo che si ripete perfettamente. In termini matematici, possiamo scrivere:

sin(x) = sin(x + 2π) = sin(x - 2π)

Quanto vale il seno di un angolo uguale a zero? Basta seguire il cerchio trigonometrico e si ha subito il risultato: sin(0°) = 0. la funzione sin(x) passa per l’origine degli assi. Non vi è nessun bisogno di eseguire un limite, basta inserire l’angolo nella funzione. Iniziamo a far crescere l’angolo. Il seno non fa che andargli dietro e continua a crescere. Fino a quando? Consideriamo la situazione in cui l’angolo raggiunge i 90° (ossia π/2 radianti, dato che 2π/4 = π/2). Siamo nel punto più alto del cerchio trigonometrico e il raggio r è proprio diretto in modo perpendicolare all’asse orizzontale. Il seno è esattamente il raggio, ossia vale 1 (ricordiamo che il raggio del cerchio trigonometrico è unitario).

Siamo in un punto veramente critico. Infatti, se l’angolo fosse leggermente più piccolo anche il seno sarebbe più piccolo. Se, l’angolo fosse appena più grande, ossia superiore anche se di poco a 90°, il seno tornerebbe a scendere. La funzione sin(x) raggiunge un massimo per x = 90° = π/2. Massimo di una curva: un concetto di importanza fondamentale nello studio delle funzioni: le derivate sembrano proprio essere nate per questo scopo. Ma… ogni cosa a suo tempo!

Continuiamo a far crescere l’angolo che adesso sta viaggiando tra 90° e 180° (tra π/2 e π). Si vede facilmente che il seno ripercorre specularmente il tragitto da 0 a π/2 e diminuisce sempre di più. Quando l’angolo giunge a 180° la situazione è analoga a quella iniziale. Il seno è sparito, ossia è tornato a zero. Potremmo dire che ha concluso il suo periodo e tutto ricomincia da capo? No, assolutamente no, dato che bisogna anche tener conto del “segno”.

Continuiamo, allora, a far girare l’angolo che inizia a essere superiore a 180°. Cosa succede al seno? Ricomincia a salire, ma nella parte bassa del grafico, ossia nella zona delle y negative. Il seno diventa, quindi, negativo. Tuttavia, a parte il segno, la sua discesa è perfettamente uguale alla salita eseguita tra 0 e 90°. Altri 90° e arriviamo a 270° (3π/2). Dovevamo aspettarcelo: il seno è nuovamente arrivato al suo valore massimo, ma con segno negativo (-1). In assoluto, questo punto è quello più basso della funzione seno e corrisponde, quindi, a un minimo della funzione. Non ci resta che percorrere l’ultimo tratto di circonferenza, quello tra 270° e 360°. Il seno diminuisce come modulo (parte positiva), ma avendo segno meno cresce verso il valore zero. Lo raggiunge quando l’angolo arriva a 360° (2π). D’altra parte 360° è esattamente uguale a 0°. Il seno ritorna alle condizioni iniziale: ha terminato il suo periodo. Continuando a far girare il raggio, non può che ripetersi la situazione precedente. E’ assolutamente inutile perdere del tempo.

Notate che la stessa cosa si otterrebbe facendo girare l’angolo in verso opposto. Percorreremmo la parte negativa delle x (angoli negativi), ma la funzione seno ripeterebbe perfettamente quanto descritto precedentemente. Insomma, possiamo fermarci qui.

Cosa possiamo concludere? Beh… innanzitutto che la funzione è periodica e che per tre volte assume il valore zero. Ha poi un massimo e un minimo, di valore numerico uguale (1) ma di segno contrario. In  fondo,  basterebbe disegnare la parte tra 0 e 90° e poi ribaltarla orizzontalmente e verticalmente per costruire la funziona finale. Non vi stupite di certo se questo tipo di curva si chiama sinusoide. E nemmeno passa inosservata la sua importanza in fisica, soprattutto per tutti quei moti periodici come la propagazione delle onde e l’oscillazione del pendolo.

Ho veramente fatto una trattazione terribilmente elementare. La maggior parte di voi mi perdoni, ma ho pensato  (e sperato) di riuscire a essere chiaro anche con gli eventuali ragazzini e di aiutarli a considerare fin dall’inizio le funzioni trigonometriche come un bellissimo gioco matematico, che si applica facilmente a giochi veri e propri come… l’altalena!

Per il coseno, possiamo essere molto più rapidi e incisivi e utilizzare le stesse figure precedenti (la curva del coseno nella Fig. 68 è quella rossa). La funzione parte da 1 per x = 0. Poi scende fino a zero per x = π/2. Diventa – 1 per x = π. Torna a zero per 3π/2 e, infine, chiude il suo periodo tornando a 1 per x = 2π. No, non state sbagliando… pensate proprio a una cosa giusta! Il coseno ha una curva perfettamente uguale a quella del seno, soltanto che è spostata tutta di π/2.

Questo fatto ci riporta a delle relazioni molto utili, che abbiamo in parte già usato e che possiamo vedere sia nel cerchio trigonometrico, sia nella rappresentazione delle due funzioni nel sistema cartesiano. Ricordiamo che il cerchio trigonometrico si divide normalmente in quattro quadranti : il primo va da 0° a 90°, il secondo da 90° a 180°, il terzo da 180° a 270° e il quarto da 270°  a 360°.

Scriviamole e verifichiamole nei due modi (lascio a voi il controllo, come semplice esercizio)

sin(90 - x ) = cos(x)

cos(90 - x) =  sin(x)

sin(90 + x) = cos(x)

cos(90 + x) = - sin(x)

sin(180 - x) = sin(x)

cos(180 – x) = - cos(x)

sin (180 + x) = - sin (x)

cos(180 + x) = - cos(x)

Continuate voi con gli altri angoli (270 +/- x e 360 +/- x) …

Facciamo, invece, insieme un altro “compitino” molto utile, ossia calcoliamo geometricamente alcuni seni e coseni di angoli particolari. Consideriamo, ad esempio, 30°, 45° e 60°. So che ormai ci sono le calcolatrici che eseguono immediatamente queste operazioni, ma applicare alcune nozioni già imparate non può che aiutare a farle diventare sempre più naturali.

Iniziamo dall’angolo di 30°, come mostrato nella Fig. 69(a) sin(30°) è dato da AH e cos(30°) da OH. Ricordiamo, infatti, che OA = 1. Ribaltiamo il triangolo OHA attorno all’asse  OH e consideriamo il triangolo OAB. L’angolo AOB è il doppio di AOH per costruzione e quindi vale 60°. Inoltre si ha che OA = OB, essendo entrambi uguali al raggio del cerchio trigonometrico. Se ne deduce che il triangolo deve essere equilatero e perciò AB = OA. Ma AB è uguale al doppio di AH per costruzione, quindi:

AB = 2AH = OA = 1

Da cui:

AH = sin(30°) = 1/2

Ricaviamo OH applicando il teorema di Pitagora al triangolo rettangolo OHA.

Abbiamo:

OH² = OA² – AH²

OH² = 1 – 1/4  = 3/4

OH = cos(30°) = √3/2

Passiamo all’angolo di 60°, considerando la Fig. 69(b). Ribaltiamo il triangolo OAH attorno ad AH e otteniamo il triangolo OAB. Nuovamente, abbiamo un triangolo equilatero, dato che ha un angolo di 60° e due lati uguali tra loro ed entrambi uguali al raggio (OA = OB = 1). Si ha immediatamente che:

2OH = OB = 1

E quindi:

OH = cos(60°) = 1/2

Dal triangolo rettangolo AHO si ricava AH

AH² = OA² – OH² =  1 – 1/4 = 3/4

e infine:

AH = sin(60°) = √3/2

Domanda: “Era proprio necessario usare la Fig. 69(b)?”. Pensateci un attimo… Ovviamente no! Bastava, infatti, ricordare le relazioni tra seno e coseno che avevamo scritto prima. In particolare, si era ricavato che:

sin(90-x) = cos(x)

e

cos(90-x) = sin(x)

Bastava, allora, scrivere:

cos(60) = sin(90 – 60) = sin(30) =1/2

sin(60) = cos(90 – 60) = cos(30) = √3/2

In poche parole, seno e coseno si invertono passando da 30° a 60° proprio perché la somma di 30° e  60° è uguale a 90° (ossia 30 = 90 -60 e 60 = 90 -30).

Usando le relazioni tra seno e coseno, possiamo facilmente calcolare il seno e il coseno di molti altri angoli tra 0° e 360°… conoscendo solo quelli di 30°. Divertitevi a farlo…

E’ immediato, infine, ricavare il valore del seno e del coseno per un angolo uguale a 45°. Basta disegnare la Fig. 69(c).

Per costruzione il triangolo AHB è rettangolo e isoscele, ossia AB = OB e, dal teorema di Pitagora:

AB² + OB² = 2 AB² = OA² = 1

E quindi:

OB² =1/2

OB = cos(45°) = 1/√2 = √2/2        (abbiamo moltiplicato sopra e sotto per √2 in modo da far sparire la radice a denominatore… di solito è conveniente …).

E quindi vale anche:

AB = OB = cos(45°) = √2/2

Seno e coseno di 45° sono uguali  e valgono √2/2. Non c’è certo da meravigliarsi!

Passiamo adesso alla funzione tangente. Già conosciamo la sua importanza in relazione al coefficiente angolare di una retta e il suo legame alla velocità in un moto rettilineo. Essa risulta decisamente meno prevedibile dei suoi colleghi seno e coseno. Cominciamo a vedere cosa le capita nel cerchio trigonometrico in Fig. 70.

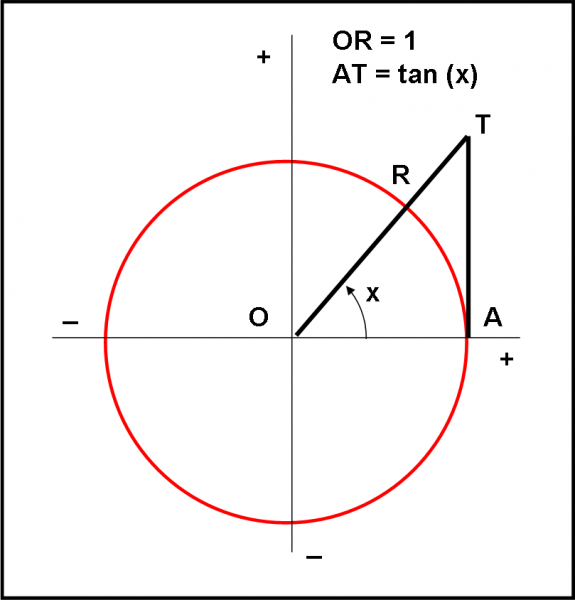
Si traccia la retta che passa per l’origine O e che forma un certo angolo x con l’asse orizzontale. Poi, si costruisce la tangente alla circonferenza nel punto A di contatto tra asse e circonferenza. Le due rette si intersecano nel punto T. La tangente è proprio il segmento AT (ponendo come sempre il raggio della circonferenza uguale a uno).

Iniziamo a far crescere l’angolo x, utilizzando le Fig. 71 e 72. All'inizio tutto bene. Sembra quasi di tracciare una curva come quella del seno. Le cose cominciano a cambiare per angoli che si avvicinano a 90° (π/2). La tangente si allunga in modo drastico. Non è difficile capire che per un angolo di 90° il segmento AT tende all’infinito. La retta OT è ormai perpendicolare all’asse x e la tangente in A  alla circonferenza può “raggiungerla” solo nel punto all’infinito, dato che sono due rette parallele. Ricordiamoci i binari del treno…

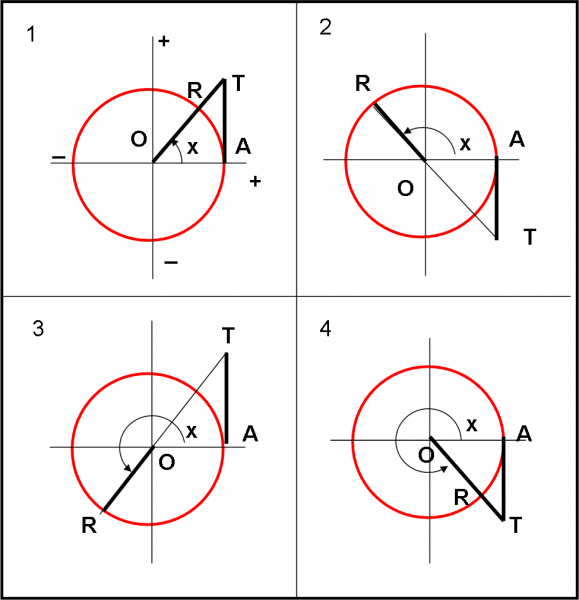
Possiamo concludere che per x che tende a 90°, provenendo dalla parte minore di 90° (o, analogamente, per x tende a 90° da sinistra), la tangente vale + ∞. In parole matematiche:

lim _x→90- tan(x) = + ∞    (ho messo il segno meno perché sto arrivando a 90° da sinistra nella Fig. 72)

Aumentiamo leggermente l’angolo, superando i 90°. Rimaniamo per un attimo interdetti… come faccio a disegnare la tangente di quell’angolo. So che devo tracciare la retta che parte da O e sottende quell’angolo con l’asse orizzontale, ma so anche che devo trovare la sua intersezione con la retta che passa per A ed è tangente alla circonferenza. Per riuscire a farlo devo prolungare la retta OA dall’altra parte e considerare la tangente in A dalla parte negativa dell’asse verticale. Non vi è altro sistema…

Mi accorgo che ho ribaltato tutto. Comunque la tangente è stata trovata ed è il segmento AT, che ha segno negativo. Non solo, però. Se mi avvicino sempre più a 90°, provenendo dalla parte destra di Fig. 72, la tangente tende nuovamente ad andare a infinito, ma dalle parte opposta di quella che avevamo costruito nel primo quadrante. In parole matematiche non possiamo che concludere che:

lim _x→90+ tan(x) = - ∞

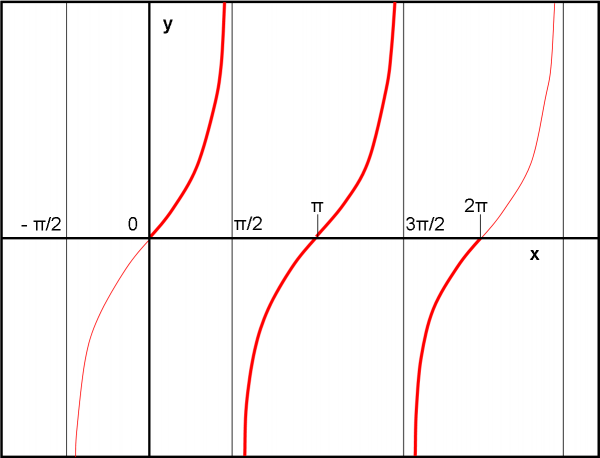
Cosa succede alla funzione che stavamo tracciando nel sistema di assi cartesiani x e y? Un bel salto improvviso. La funzione salta da + ∞ a - ∞. Sappiamo come definirla: non è una funzione continua in x = 90°. Possiamo anche dire che la retta perpendicolare all’asse x , descritta da x = π/2 è un asintoto verticale per la funzione tan(x). Infatti, la funzione tende a raggiungerla sia da un lato che dall’altro, ma riesce a farlo solo nei suoi punti all’infinito.

Chi se l’aspettava da una funzione così apparentemente semplice? Mai fidarsi delle acque chete…

Non ci resta che andare avanti e sperare che le cose si tranquillizzino. Continuiamo a far crescere l’angolo che ormai sta viaggiando verso 180° (π). Quello che otteniamo è una diminuzione del segmento AT (ossia della tan(x)) che da valori molto negativi tende a zero. Per x = 180° siamo proprio a zero, così come eravamo quando siamo partiti da x = 0°. Forza e coraggio e andiamo avanti. La tangente ricomincia a crescere verso valori positivi sempre più grandi. Non ci stupiamo più se vicino a 270° succede un fattaccio perfettamente uguale a quanto successo a 90°. La tangente salta da + ∞ a - ∞.

Tiriamo un sospiro e continuiamo, sapendo già dove andremo a finire. Ormai stiamo seguendo pari pari quello che abbiamo fatto muovendoci da 90° a 180°. Conclusione più che ovvia (e aspettata) a 360° la tangente torna a zero. Beh… meno male, questa sembra la cosa più logica trovata finora.

Guardiamo un attimo ciò che abbiamo disegnato nella Fig. 72. Una curva sicuramente strana, ma che ha un vantaggio non indifferente: essa si ripete esattamente dopo 180°. In altre parole, il suo periodo è di solo 180°. Notiamo anche un andamento veramente “elegante” intorno a 0 e π. Una specie di piccola onda, dove cambia il modo di curvare… Non diciamo altro, ma ne vedremo cose di questo tipo nello studio di funzioni…

Abbiamo fatto una bella fatica a disegnare la curva relativa alla funzione y = tan(x). Potevamo ottenere lo stesso risultato -e ben più velocemente- usando la matematica e la trigonometria già conosciuta. Non arrabbiatevi… in fondo è stato divertente…

Sappiamo, infatti, che la tangente non è altro che il rapporto tra seno e coseno. Possiamo, allora, scrivere direttamente

y = tan(x) = sin(x)/cos(x)

Senza bisogno di tante figure, basta sostituire a x l’angolo che varia da 0° a 360° e ricordare quanto abbiamo appena ricavato, all’inizio dell’articolo, sulle funzioni seno e coseno.

Per x = 0, sin(x) = 0 e cos(x) = 1, cioè:

tan(0) = 0/1 = 0

Andiamo a x = π/2. sin(x) = 1, cos (x) = 0. Ne segue:

tan(π/2) = 1/0 = + ∞

Tuttavia, per x leggermente più grande di 90° il coseno cambia di segno, quindi il passaggio al limite ci dice che vale anche y = - ∞ (dipende solo da che parte ci avviciniamo a π/2…)

Per essere più esatti:

tan(π/2)- = lim _{x →π/2-}tan(x)= 1/0 = + ∞

tan(π/2)+ = lim _{x →π/2+} tan(x)= 1/0- = - ∞

Per x = π abbiamo sin (x) = 0, cos(x) = -1 e quindi:

y = 0/-1 = 0

A 270°  si ha:

tan(3π/2)- = lim _{x →3π/2-}tan(x)= -1/0- = + ∞

tan(3π/2)+ = lim _{x →3π/2+} tan(x)= -1/0+  = - ∞

Infine, a 360°:

tan(2π) = 0/1 = 0

Come volevasi dimostrare…

Tanto per non trattare diversamente la tangente, calcoliamo anche per lei il valore che assume per qualche angolo particolare (i soliti 30, 60, 45).

Abbiamo bisogno di figure? Direi proprio di no. Basta ricordare che: tan(x) = sin(x)/cos(x).

Ne segue che:

tan(30) = sin(30)/cos(30) = (1/2)/(√3/2) = 1/√3 = √3/3 (sempre per far sparire la radice al denominatore…).

tan(60) = sin(60)/cos(60) = (√3/2)/(1/2) =  √3

tan(45) = sin(45)/cos(45) = (√2/2)/(√2/2) = 1

Beh… era del tutto inutile scrivere quest'ultima relazione, dato che sappiamo che il seno e il coseno di 45° sono uguali e quindi il loro rapporto non può che essere uno. Dalla curva della funzione tangente (o dal cerchio trigonometrico) si può facilmente concludere che:

tan (x) = tan (x + π) = tan (x – π).

D’altra parte sappiamo che la tangente ha un periodo di π.

Facciamo un piccolo riepilogo.

Le funzioni seno e coseno sono entrambe  “confinate” tra -1 e +1. Non hanno punti strani o bisogno di eseguire limiti (trascurando i massimi e minimi, per adesso). Entrambe si ripetono con un periodo di 2π. Sono praticamente uguali, mostrando solo uno sfasamento di π/2.

La funzione tangente, invece, malgrado non sia altro che il rapporto tra le prime due è veramente “pazzerella”. Non solo viaggia tra -∞ e +∞, ma salta da un valore all’altro con una spavalderia inimmaginabile. Essa ha bisogno dei limiti e addirittura dei limiti destro e sinistro. In compenso, si ripete con un periodo di solo π.

Come già detto, le funzioni trigonometriche sono fondamentali per descrivere tutti i moti circolari e oscillatori. Ne incontreremo sicuramente qualcuno. Ma non solo… ovviamente. Ci sarebbero ancora parecchie relazioni che si potrebbero ricavare tra queste semplici funzioni così come si potrebbero anche introdurre le funzioni inverse e altre ancora. Per adesso, fermiamoci qui. Se ne avremo bisogno faremo in fretta a descriverle… Ormai, abbiamo le basi per affrontare la trigonometria anche più complessa e -magari- anche quella sferica, così utile per le trasformazioni  delle coordinate astronomiche (chiedete alle eclissi mutue dei satelliti di Giove…).

Direi che siamo pronti per entrare nella grande casa delle derivate. Un consiglio: andate a rileggervi con calma tutta la parte sui limiti, dato che ripartiremo da lì…

P.S: ho volutamente usato nel testo sia angoli espressi in gradi che in radianti. L’ho fatto per abituarci sempre più alla loro perfetta uguaglianza… la differenza è solo formale.

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica